基于EMD的仪器稳定度组合预测

2015-03-11CombinedPredictionBasedonEMDforInstrumentStability

自动化仪表 2015年1期

关键词：支持向量机

Combined Prediction Based on EMD for Instrument Stability

程双江　李世平　邬肖敏

(第二炮兵工程大学，陕西西安　710025)

基于EMD的仪器稳定度组合预测

Combined Prediction Based on EMD for Instrument Stability

程双江李世平邬肖敏

(第二炮兵工程大学，陕西西安710025)

摘要：为更好地把握仪器的性能变化规律，规避其可能带来的各种风险，将预测理论应用到仪器稳定度预测中，建立了一种基于EMD-SVM的稳定度组合预测模型。首先利用EMD方法对稳定度数据进行分解，然后对分解得到的数据选择一种预测模型进行预测，最后再把所有这些分解数据的预测结果输入到SVM中进行组合预测。通过与移动平均模型、自回归积分滑动平均(ARIMA)模型和线性组合预测模型的预测结果相比较，验证了该方法的有效性。

第一作者程双江(1989-)，男，现为第二炮兵工程大学仪器与科学技术专业在读硕士研究生；主要从事预测方面的研究。

关键词：仪器稳定度经验模态分解(EMD)支持向量机(SVM)组合预测预测精度

Abstract：In order to better grasp the regular pattern of the performance variation of the instruments, and to evade various risks may occur, the prediction theory is applied in the prediction of instrument stability, and the combined prediction model based on EMD-SVM is built. Firstly, the data of stability are decomposed by adopting EMD method; then a prediction model is selected from the data obtained by decomposition for predicting; finally all the predicted results of decomposed data are put into SVM for combined prediction. The comparison of the predictive results from moving average model, autoregressive integrated moving average (ARIMA) model and linear combination forecasting model, proves the effectiveness of this method.

Keywords：InstrumentStabilityEmpirical mode decomposition(EMD)Support vetor machine(SVM)Combined predictionPrediction accuracy

0引言

仪器作为人类认识世界必不可少的工具，如今已被广泛应用于我们生活的各个领域。但是仪器在给社会带来巨大利益的同时，其自身也会出现一系列的问题，如果不注意这些问题，带来的损失同样不可估量。因此,依据仪器性能指标参数的历史数据，对其未来可能的发展趋势作出预测就显得格外重要。对于如今的高精度智能仪器而言，稳定度指标已经逐步成为用户最关心的话题，因此本文对仪器稳定度数据进行研究，具备更大的工程与现实意义。

目前，关于预测的研究很多[1-3]，但主要还是组合预测，比如基于神经网络的组合预测、基于支持向量机(support vector machine,SVM)的组合预测等。其中,SVM在解决小样本、过拟合和维数灾变等问题中具有不可比拟的优势[4-6]，因此本文选择了基于SVM的组合预测模型对稳定度数据进行预测。首先利用经验模态分解(empirical mode decapmosition,EMD)方法对稳定度数据进行分解，然后对分解得到的3种不同类型的数据分别采用多项式模型、BP神经网络模型和自回归积分滑动平均(autoregressive integrated moving average,ARIMA)模型进行单独预测，最后再将单独预测的结果输入到SVM中进行组合预测，最终建立了基于EMD-SVM的组合预测模型。

1EMD方法和SVM简介

1.1　EMD方法

EMD是将非平稳、非线性信号分解成一系列表征信号特征时间尺度的IMF，使得每个IMF是单分量的幅值或频率调制信号。简单来说，就是将原始信号中不同尺度的波动或趋势项逐级分解，产生一系列具有不同特征尺度的数据序列，每一个序列就是一个IMF。

相比于小波分解等其他信号分解方法而言，EMD在信号分解过程中分解的基函数是不确定的。EMD依据的是信号本身的局部信息特征进行自适应分解，不需要预先设定基函数，也无需信号的任何先验知识。因此，EMD具有更好的自适应性，在处理非线性、非平稳信号方面具备更大优势[7-8]。对信号x进行EMD分解的具体步骤如图1所示，其实质就是一个筛选过程，通过一个停止准则对IMF进行不间断的筛选。

图1　EMD流程图

1.2　SVM简介

支持向量机(SVM)是基于统计学习理论发展起来的一种新型机器学习方法，它建立在统计学习理论的VC维和结构风险最小化的理论基础之上。由于SVM在一定程度上克服了“维数灾难”和“过学习”等困难，并且在解决小样本问题上具有不可比拟的优势，因此目前SVM已被广泛应用于模式识别、函数逼近、数据挖掘和非线性系统控制等领域中[9-11]。

SVM预测的本质是通过非线性变换，将非线性问题映射到高维特征空间中，从而转换为线性问题进行求解。

SVM预测可表示为如下二次规划问题。

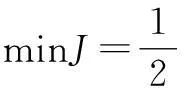
(1)

约束条件：

(2)

式中：n为样本总数；ξi，ξi*为松弛因子；C为惩罚因子。

考虑到直接对此式进行求解存在一定的困难，为此引入拉格朗日因子，将其转化为凸二次规划问题求解。

(3)

那么SVM函数就可以表示为：

(4)

引入核函数K(xi,xj),将其转化到高维特征空间中，用K(xi,xj)代替ψ(xi)ψ(xj)，则式(4)可以转化为式(5)进行求解。

(5)

这样就实现了数据从低维到高维之间的数据转换(非线性映射)，达到样本学习的目的。

2基于EMD-SVM的组合预测原理

假设EMD分解后得到的信号为IMF1、IMF2和RES，那么基于EMD-SVM的原理图如图2所示。

图2　EMD-SVM组合预测原理图

组合预测方法是建立在多种单一预测模型基础之上的。组合预测的理论已经证明，多种单一模型的组合在一定的条件下能更有效地改善模型的拟合能力，提高预测精度[12]。而要想提高最终的组合预测模型的预测精度，单一模型的预测好坏是前提，因此必须首先选择恰当的单一模型进行预测。

要建立基于EMD-SVM的组合预测模型，首先需要采用EMD方法对原始稳定度数据进行分解，得到相对较为简单的分解数据，比如说趋势项、周期项、随机项等；其次再针对这些分解得到的数据分别选用精度较高的预测方法；最后再将这些分解信号的单一模型预测结果输入到SVM中进行非线性组合，实现基于EMD-SVM的组合预测。

如图2所示，假设经过EMD分解后得到的信号有3个，那么就分别采用一种预测方法进行针对性的预测，得到的预测结果分别为y1、y2、y3。非线性组合的预测结果可以表示为：

y=F(y1,y2,y3)

(6)

式中：F为SVM组合预测函数。

这样就基本实现了针对仪器稳定度数据这类非线性、非平稳时间序列的分解，单一预测到组合预测的整体过程。

3基于EMD-SVM的仪器稳定度预测

计量标准仪器不仅需要作为检定其他仪器设备的依据，作为中间环节，还需要将测量结果在允许的范围内溯源到国家计量基准。因此，对计量标准仪器进行预测研究具备更大的工程与现实意义。同时，鉴于高稳时频晶振的稳定度指标在使用的过程中尤为重要，本文的仿真试验采用的是某计量站高稳时频晶振计量标准仪器的稳定度数据。

数据来源于该仪器每年一次的上级单位检定数据(作为第一季度数据)，以及两次检定期间该计量站计量员利用更高精度的计量标准每季度进行一次的检定数据(第一季度除外)。从2002年到2012年总共44个数据点，以2002~2011年的40个数据点进行稳定度拟合，建模预测2012年4个季度的稳定度值，然后进行结果比对分析，如表1所示。

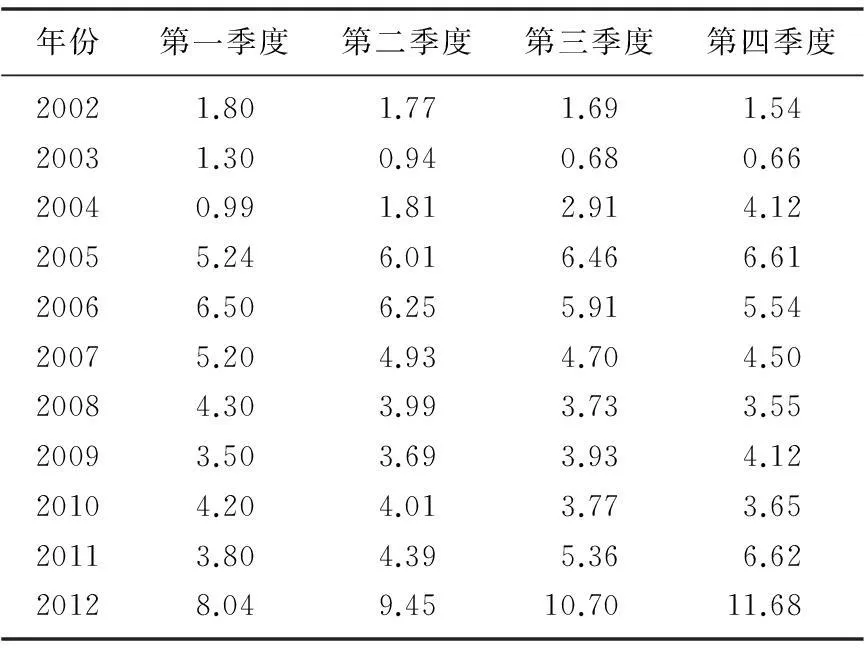
表1　高稳时频晶振2002~2012年稳定度值

首先进行EMD分解，分解结果如图3所示。EMD分解得到了IMF1、IMF2和RES三个分量，其中IMF1和IMF2为IMF分量，RES为剩余分量。经过计算得到分解造成的各点的累计误差和为-1.77×10-15，相比于预测误差可以忽略不计。从图3可以看出，IMF1变化规律较为复杂，因此预测起来也相对比较困难，需要着重考虑。最终通过比较选择了效果较好的ARIMA模型进行预测。IMF2为近似周期项，预测较为简单，本文采用的是BP网络对其进行预测。RES可以认为是趋势项，预测更为简单，直接选用传统的多项式模型进行预测。

图3　EMD分解结果

首先对IMF1进行预测，然后再依次对IMF2和RES进行预测。对IMF1进行预测时，由于变化规律比较复杂，采用ARIMA模型进行预测。首先需要进行去平稳化差分处理，然后再进行模型的定阶，模型的定阶通过AIC准则确定，最终设定的模型参数(p,d,q)为(1,1,3)，用前40个数据点进行拟合，最终得到的拟合曲线如图4所示。从图4可以看出，ARIMA模型对IMF1拟合效果相对较好。

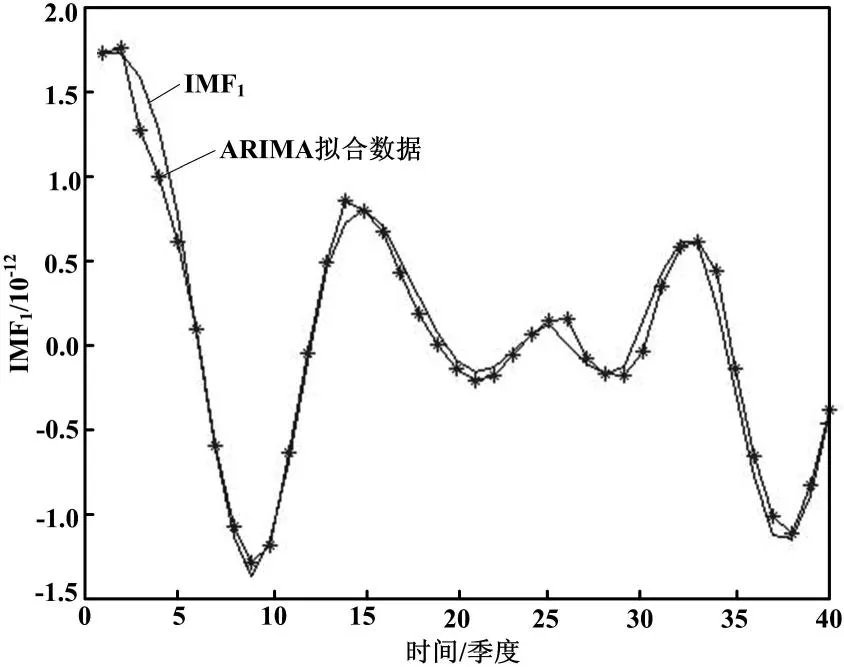
图4　IMF2拟合

对IMF2和RES进行建模，采用BP网络模型和多项式模型得到的拟合曲线分别如图5和图6所示。从图5和图6可以看出，拟合精度更高。

图5　IMF2拟合曲线

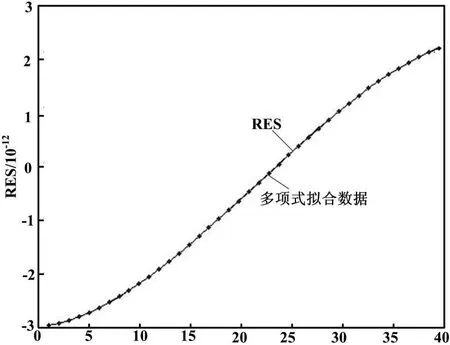
图6　RES拟合曲线

采用ARIMA模型、BP网络模型和多项式模型分别实现了IMF1、IMF2和RES的建模拟合。将建立的模型用于后4个点数据预测，与EMD分解后得到的IMF1、IMF2和RES后4个数据点的实际值进行比较，结果如表2所示。

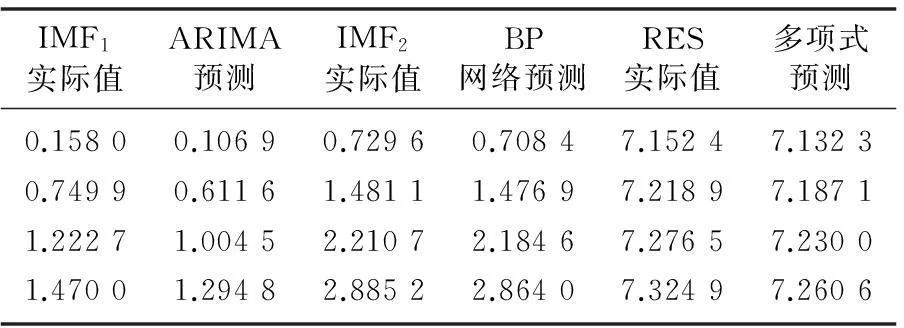
表2　单一模型后4个数据点预测结果

从表2可以看出，单一模型预测效果较好，仅仅对IMF1进行预测时预测误差相对稍大，因此可以将3种单一模型预测结果作为输入，利用RBF核函数SVM进行非线性组合预测，采用遗传算法(genetic algorithm,GA)对SVM参数进行寻优，得到的最优惩罚因子C和核函数参数δ分别为88.35和11.47，那么最终建立的基于SVM的非线性组合预测结果如图7所示。图7中，前40个为拟合数据，后4个为预测数据。

图7　基于EMD-SVM的组合预测

从图7可以看出，EMD方法预测效果较好，精度较高。为了更直观地观测其预测效果，将2012年后4个季度的稳定度预测值以具体数值展现。同时,为了验证该EMD-SVM预测模型的有效性，分别与单一的移动平均模型、ARIMA模型和线性组合预测模型的预测结果进行了比较，结果如表3所示。

表3　几种模型预测结果

以平均相对误差作为衡量标准，经过计算，4种模型的平均预测相对误差分别为26.5%、2.94%、1.97%和1.4%。可以看出，组合预测模型相对与单一预测模型而言，预测精度得到了大幅提升，而基于EMD-SVM的非线性组合预测模型相比线性组合预测模型，精度更高。因此,可以认为对高稳时频晶振仪器稳定度数据进行预测时，采用EMD-SVM的非线性组合预测模型效果较好。

4结束语

基于仪器设备在现实生活中发挥的巨大作用，为了规避其可能带来的风险，本文就仪器稳定度数据展开分析，结合历史数据对其可能出现的规律进行预测，

实现了基于EMD-SVM的仪器稳定度非线性组合预测。仿真结果表明，该方法预测效果较好、精度较高。对仪器稳定度数据的预测，对于指导企业生产、避免各类事故发生等具有重大的现实意义，但还有待于进一步的研究探索。

参考文献

[1] 高宁，崔希民，高彩云.灰时序GM-AR模型在建筑物沉降变形预测中的应用[J].测绘科学，2013，38(1)：139-141.

[2] 华静，艾莉，程加堂.神经网络组合模型在大坝位移预测中的应用[J].科学技术与工程，2013，2(4)：1091-1093.

[3] 周伟萍，王丰效.灰色DNGM(1,1)预测模型及其优化[J].计算机工程与应用，2013，49(10)：28-31.

[4] 甘旭升，端木京顺，丛伟，等.基于ARIMA与SVM的飞行事故组合预测方法[J].中国安全科学学报，2011，21(7)：79-81.

[5] 陈涛.基于DE-SVM非线性组合预测模型的研究[J].计算机工程与应用，2011，47(13)：33-36.

[6] 朱莎，刘晓.小波分析和支持向量机组合法预测应急血液需求研究[J].中国安全科学学报,2013，23(5)：166-170.

[7] 余伟凯.EMD时频分析方法的理论研究与应用[D].秦皇岛：燕山大学，2006.

[8] 王婷.EMD算法研究及其在信号去噪中的应用[D].哈尔滨：哈尔滨工程大学，2010.