基于状态的维修在导弹保障中的有效性分析
2015-03-11陈兆铭
陈兆铭 马 亮 徐 阳
(1.海军潜艇学院 青岛 266000)(2.91880部队 胶州 266300)
基于状态的维修在导弹保障中的有效性分析
陈兆铭1马 亮1徐 阳2
(1.海军潜艇学院 青岛 266000)(2.91880部队 胶州 266300)
导弹维修保障系统是一个复杂的非线性系统,采用系统动力学仿真的方法能够清晰地表达出系统要素之间的相互关系,可以有效地对此类复杂维修保障系统的保障行为特征进行(动态的)仿真。论文通过分析导弹维修保障系统各要素之间的相互关系,建立了其保障行为特征的动力学模型,并通过实例验证了基于状态的维修在提高导弹维修保障的有效性方面具有明显的优势。
基于状态的维修; 系统动力学; 导弹
Class Number E920
1 引言
随着导弹武器装备的更新换代,传统的维修方式越来越难以应对导弹的保障任务,且保障时间和费用也大大增加。同时,随着维修新技术的发展进步,近年来出现了“基于状态的维修”,即CBM。由于CBM具有传统维修难以具备的优势,从一出现就受到广泛的关注,甚至被认为是未来一些复杂装备的首选维修方式[1]。基于CBM的导弹保障系统主要研究导弹的维修模型和决策方法,解决现行的保障模式中难以解决的问题,以提高保障效率,降低保障费用。
导弹保障系统是一个复杂的非线性系统,一般的仿真方法难以描述系统中各个要素之间错综复杂的关系,因此必须从系统的整体与部分之间相互依赖、相互制约的关系出发,研究系统的动态变化。对于同类装备的维修系统,尽管故障的发生是离散的,但从整体角度看,系统中仍然存在着大量连续过程,例如装备性能退化、维修需求变化、维修资源供应等,因而可采用动力学仿真的方法对装备维修系统进行建模和分析[2]。
2 基于状态的维修
2.1 基于状态维修的定义
基于状态的维修(Condition Based Maintenance,CBM)[3]是通过内置的传感器或便携式外部设备进行测试,对系统状态实时或接近实时评估的维修过程。其特点是基于装备的实时状态,应用状态监测技术和故障诊断技术,按诊断程序来确定装备的“健康状态”[4]。
2.2 装备状态
装备在使用过程中的状态大致分为功能故障状态、潜在故障状态和正常状态三种。
1) 功能故障状态是可以直接反映装备发生了功能故障的状态,在此状态下,装备中的预定功能不能按规定的标准实现。
2) 潜在故障状态是装备从正常状态向功能故障状态发展的过渡状态,在此状态下,装备的预定功能虽然还能在一定程度上实现,但装备内部已出现早期故障或损伤,其性能在逐渐衰退和劣化。
3) 正常状态是从安装到发生潜在故障之间装备所表现出的状态,在此状态下,装备可正常运行。
2.3 P-F曲线
通常,装备的退化是一个逐渐劣化的过程,图1说明了故障的阶段情况,即P-F曲线[5]。该曲线显示了故障如何开始,并退化到可以被探测到的过程,若故障点“P”没有被探测到而未采取任何修正措施,通常会以更快的速度退化到功能故障点“F”。“P-F间隔”是从潜在故障发生(发现缺陷)到演变成为功能故障之间的时间间隔。
当装备出现问题时,如果能够及时发现并处理,将极大地减少维修费用。因此,当潜在故障可探测点距离功能故障点越远(即P-F间隔越大),装备发生故障的可能性越小,维修费用越少;反之,潜在故障可探测点越靠近装备功能故障点时(即P-F间隔越小),装备发生功能故障的可能性越大,同时所需的维修费用也随之剧增。
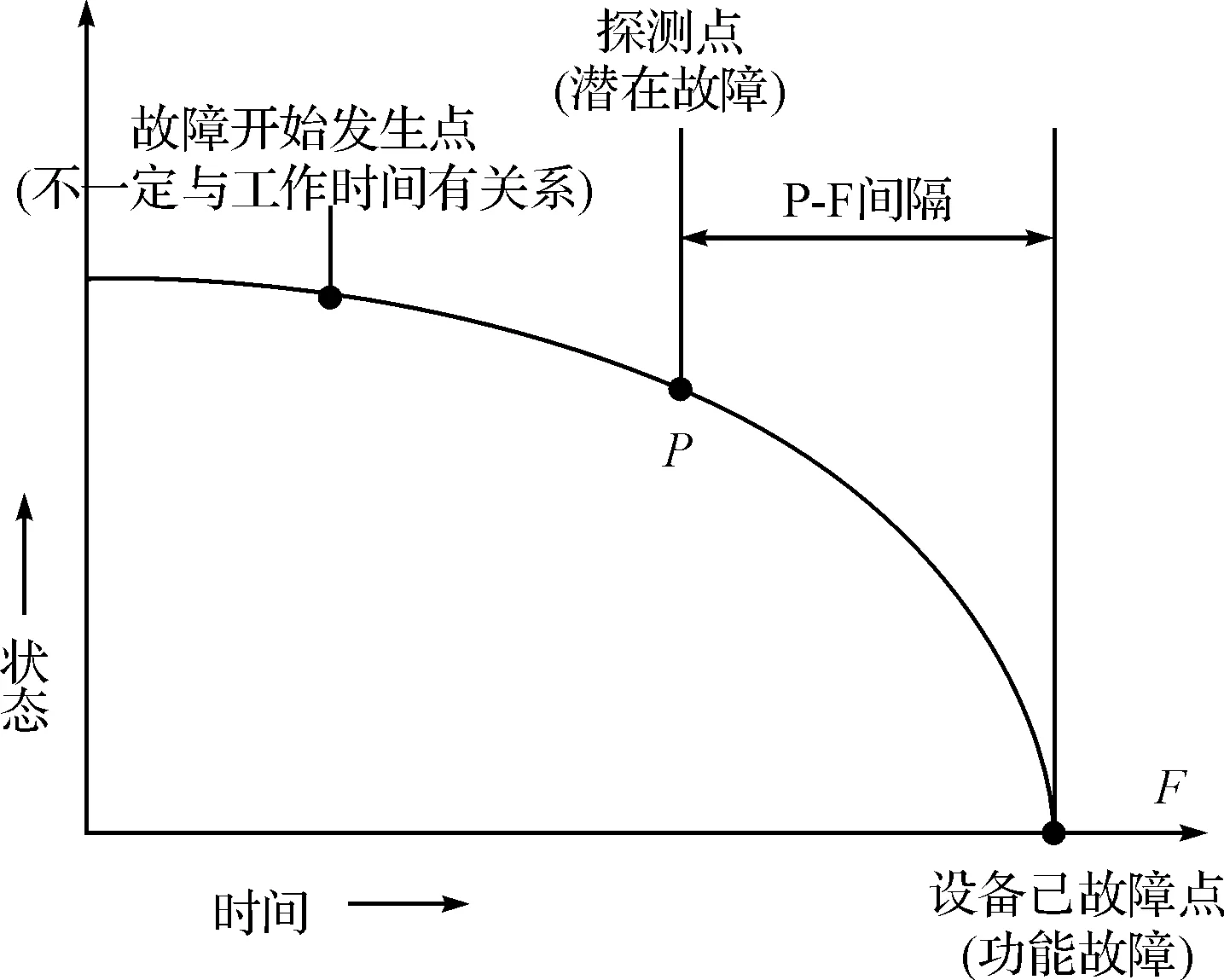
图1 P-F间隔
3 系统动力学
系统动力学[6](System Dynamics,SD)是美国麻省理工学院的J. W.弗雷斯特教授最早提出的一种对社会经济问题进行系统分析的方法论和定性与定量相结合的分析方法。
3.1 系统动力学的基本原理
系统动力学采用模拟技术,以结构-功能模拟为其突出特点。一反过去常用的功能模拟(也称黑箱模拟)法,建模从系统的内部结构入手,构造系统的基本结构,进而模拟与分析模型系统的动态行为。这样的模拟更适于研究复杂系统随时间变化的问题。系统动力学从真实系统的因果环中得出模型的构造,弱化了数据要求,使能够利用它对现实系统(即使这个系统是“灰色”的,缺乏长期、稳定、全面的统计数据)进行定量研究,而不苛求数据的十分精确,而且模型结构设计较为简单,操作起来较为方便。
3.2 系统动力学模型的基本构成
1) 因果关系图
因果链:连接因果关系的有向线段。箭尾始于原因,箭头终于结果,一条正(+)因果链意味着若A增加B也增加或若A变化使B在同一方向上发生变化,如图2所示。一条负(-)因果链意味着意味着若A增加B则减少或若A变化使B在相反的方向上发生变化,如图3所示。

图2 正(+)因果链

图3 负(-)因果链
因果(反馈)回路。原因和结果的相互作用形成因果关系回路。如图4所示,因果反馈回路有正负两种极性,若反馈回路中包含偶数个负的因果链,则其极性为正;若反馈回路中包含奇数个负的因果链,则其极性为负。

图4 因果(反馈)回路
2) 系统动力学关系流图
流图是系统动力学模型的基本形式,通常由水平变量、速率变量、辅助变量等符号构成,直接形象地反映系统结构和动态特征。不仅提供了系统结构和系统行为之间相互关系的直观解释,提供了从定性和定量两方面描述系统行为的可能性。
3.3 系统动力学模型的建模步骤
在运用系统动力学进行建模,要明确系统动力学建模的目的是为了分析系统的问题,加深对系统内部结构和其动态行为的关系的认识,并进行改善系统行为的研究。建立系统动力学结构模型的一般步骤为如图5所示。
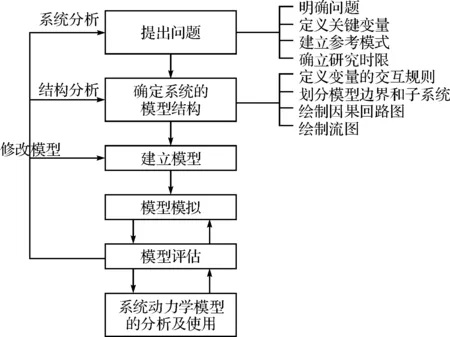
图5 系统动力学建模步骤
4 导弹保障系统动力学模型
4.1 提出问题
利用系统动力学方法,建立基于CBM的导弹保障系统模型,是为了说明基于状态的维修在导弹保障系统的作用机制和影响程度。系统动力学认为,内因决定了系统的行为,外因往往起不到决定性的作用[7]。因此,在建模前,首先要对模型的边界进行确定,忽略那些不是很重要的因素。选择合理的系统边界是关系到模型成功与否的关键[8]。假设条件如下:
1) 导弹有正常、退化和故障3种状态;
2) 系统中存在事后维修、定期维修和基于状态的维修,定期维修为辅助基于状态的维修而存在;
3) 对检测出异常退化状态的导弹进行基于状态的维修,对未检测出异常状态的导弹进行定期维修,对故障状态的导弹进行事后维修;
4) 不考虑突发性故障;
5) 不考虑人力资源约束和维修管理体制约束。
4.2 系统的模型结构
1) 因果反馈图

图6 基于CBM的导弹保障系统模型因果关系图
初始时,导弹都是正常无故障的,这就是反馈回路中的“正常状态的导弹”。受贮存环境和作战训练使用等因素对导弹的影响,部分“正常状态”的导弹出现潜在故障,形成“退化状态的导弹”。于是,在反馈回路中加入“基于状态的维修”,对检测出存在潜在故障的导弹进行及时的预防性维修。由于受装备的状态监测技术和故障预测和诊断能力等条件的限制,难免会出现部分导弹已进入退化状态,但仍未检测出异常的情况。考虑到此种情况的存在会对导弹的贮存和作战训练使用时造成危害,因此在反馈回路中采用传统的“定期维修”对未检测出故障的导弹进行维修,以减少这种情况发生;对发现已出现功能故障的导弹进行“事后维修”。因此,对导弹维修保障过程中进行基于状态的维修、定期维修和事后维修的导弹共同构成反馈回路中的“正常状态的导弹”。
2) 系统的参数和变量
根据系统动力学模型建立的需要,基于上文对正常状态导弹影响因素的因果关系研究,建立系统的变量集,即定义关键变量和模型的水平变量、速率和辅助变量,如表1所示。
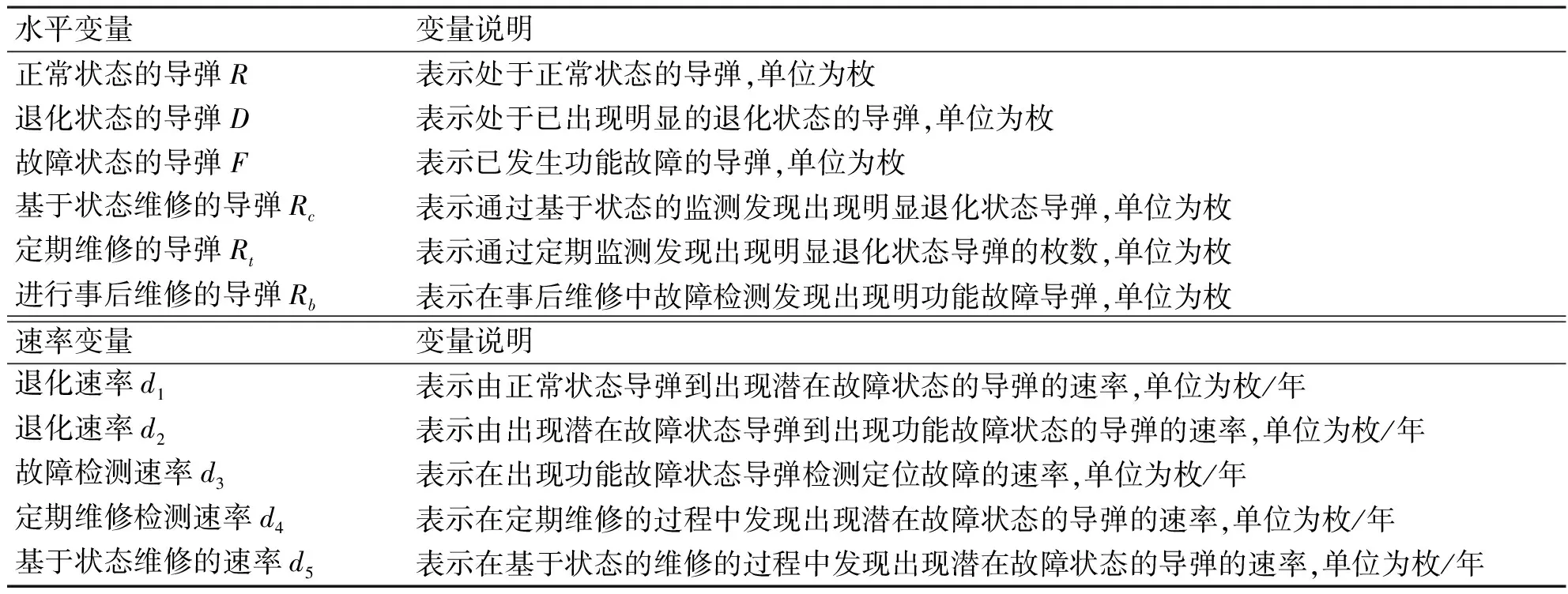
表1 基于CBM导弹保障系统水平、速率和辅助变量集
续表1
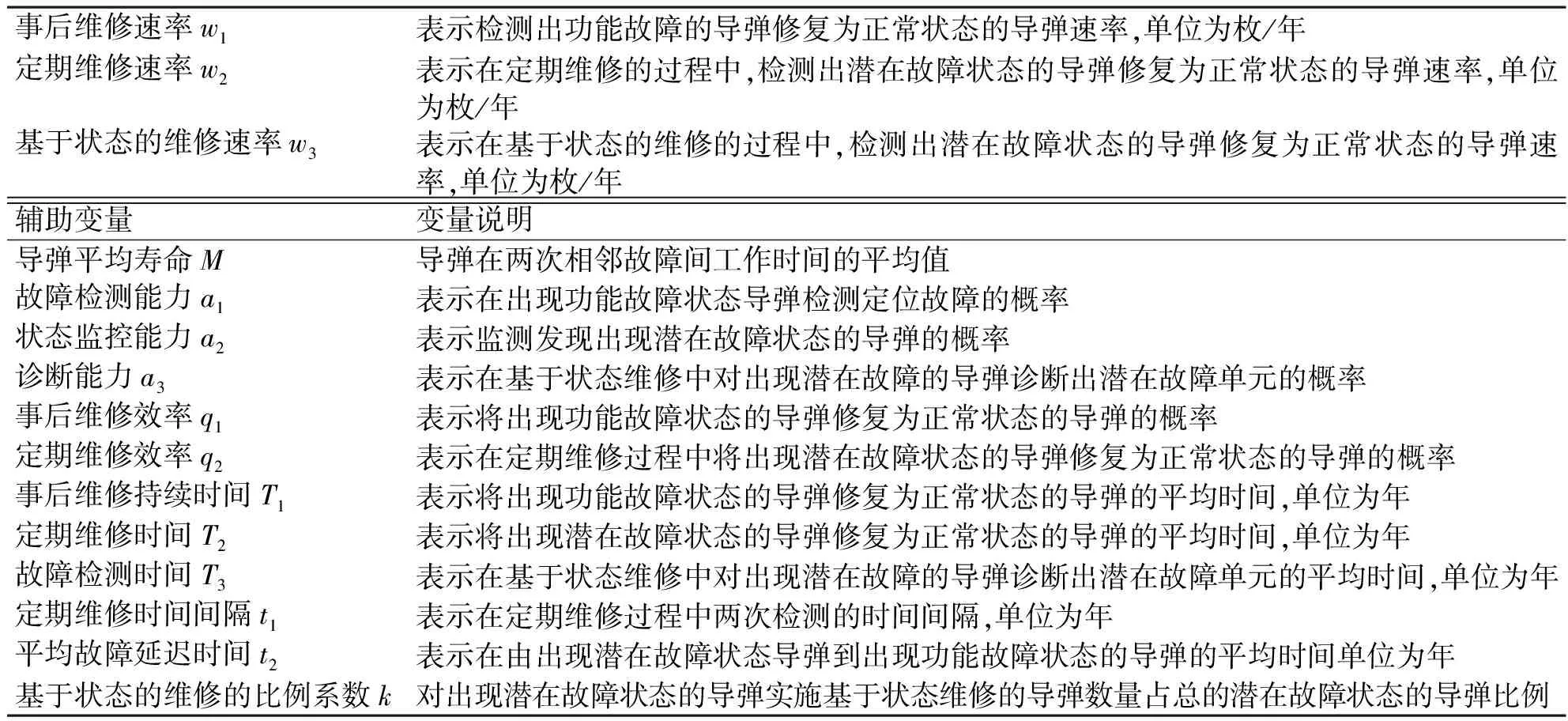
事后维修速率w1表示检测出功能故障的导弹修复为正常状态的导弹速率,单位为枚/年定期维修速率w2表示在定期维修的过程中,检测出潜在故障状态的导弹修复为正常状态的导弹速率,单位为枚/年基于状态的维修速率w3表示在基于状态的维修的过程中,检测出潜在故障状态的导弹修复为正常状态的导弹速率,单位为枚/年辅助变量变量说明导弹平均寿命M导弹在两次相邻故障间工作时间的平均值故障检测能力a1表示在出现功能故障状态导弹检测定位故障的概率状态监控能力a2表示监测发现出现潜在故障状态的导弹的概率诊断能力a3表示在基于状态维修中对出现潜在故障的导弹诊断出潜在故障单元的概率事后维修效率q1表示将出现功能故障状态的导弹修复为正常状态的导弹的概率定期维修效率q2表示在定期维修过程中将出现潜在故障状态的导弹修复为正常状态的导弹的概率事后维修持续时间T1表示将出现功能故障状态的导弹修复为正常状态的导弹的平均时间,单位为年定期维修时间T2表示将出现潜在故障状态的导弹修复为正常状态的导弹的平均时间,单位为年故障检测时间T3表示在基于状态维修中对出现潜在故障的导弹诊断出潜在故障单元的平均时间,单位为年定期维修时间间隔t1表示在定期维修过程中两次检测的时间间隔,单位为年平均故障延迟时间t2表示在由出现潜在故障状态导弹到出现功能故障状态的导弹的平均时间单位为年基于状态的维修的比例系数k对出现潜在故障状态的导弹实施基于状态维修的导弹数量占总的潜在故障状态的导弹比例
3) 流图
流图的结构比因果反馈图更能反映基于CBM的导弹保障系统的结构。为了进一步量化系统内变量间关系,下面就实际流程来说明对基于CBM的导弹维修保障系统的机理的动态认识过程。
图7所示的系统动力学流图模型是图6因果关系的量化表述,充分分析了基于CBM的导弹维修保障过程中各状态变量、速率变量,更加清晰地表示出传递结构和反馈控制关系。

图7 基于CBM的导弹保障系统流图
4.3 模型建立
图7虽然能直观地描述系统要素的因果关系和系统结构,但不能显示系统变量之间的定量关系,不能完全定量描述系统的动态行为,因此还要用结构方程式进一步描述。
由图7可得到正常状态导弹R的状态方程为
R(t+1)=R(t)+[w1(t)+w2(t)+w3(t)-d1(t)]
(1)
其中,t和t+1为相邻1个时间单位的节点。
在退化速率d1和退化速率d2之间存在一个状态变量退化状态D,表示正常状态R在P点之后到F点之前的某一时刻检测到出现潜在的故障状态的导弹的数量,其输入速率为d1,输出速率为d2。因此,可得到退化状态导弹D的状态方程:
D(t+1)=D(t)+[d1(t)-d2(t)-d4(t)-d5(t)]
(2)
故障状态导弹F的状态方程:
F(t+1)=F(t)+[d2(t)-d3(t)]
(3)
进行基于状态的维修的导弹Rc的状态方程:
Rc(t+1)=Rc(t)+[d5(t)-w3(t)]
(4)
进行定期维修的导弹Rt的状态方程:
Rt(t+1)=Rt(t)+[d4(t)-w2(t)]
(5)
进行事后维修的导弹Rb的状态方程:
Rb(t+1)=Rb(t)+[d3(t)-w1(t)]
(6)
模型初始时,导弹都处于正常状态,还尚未出现潜在故障状态和故障状态的导弹,因此,正常状态的导弹初始数量R(0)=100,退化状态的导弹D(0)=0,故障状态的导弹F(0)=0,实施基于状态的维修的导弹Rc(0)=0,实施定期维修的导弹Rt(0)=0,实施事后维修的导弹Rb(0)=0。当潜在故障出现,则退化速率d1>0,在维修保障条件允许时进行基于状态的维修和定期维修。当维修保障条件不允许、未检测出导弹的潜在故障时,由于贮存环境和导弹的作战训练使用,就会使其退化至出现功能故障状态则需进行事后维修。
根据速率变量对状态变量的累积作用,可得以下方程。
退化速率d1的方程:
d1(t)=R(t)/M
(7)
退化速率d2的方程:
d2(t)=(1-a2)D(t)kt/t1
(8)
故障检测速率d3的方程:
d3(t)=a1F(t)
(9)
定期维修检测速率d4的方程:
d4(t)=(1-k)D(t)a2k/t2
(10)
检测出潜在故障速率d5的方程:
d5(t)=a2kD(t)/t1
(11)
事后维修速率w1的方程:
w1(t)=q1Fb(t)/T1
(12)
定期维修速率w2的方程:
w2(t)=q2Rt(t)/T2
(13)
基于状态的维修速率w3的方程:
w3(t)=a3Rc(t)/T3
(14)
由图7可看出,各速率变量对水平变量的影响。事后维修的速率w1,定期维修的速率w2,基于状态的维修速率w3作用是使正常状态的导弹R增加;退化速率d1、退化速率d2的作用是使处于正常状态的导弹数量R减少;检测故障的速率d3的作用是使进行事后维修的导弹的数量Rb积累量增加,定期速率速率d4的作用,是使进行定期维修的导弹数量Rt积累量增加。检测出潜在故障的速率d5的作用是使进行基于状态的维修的导弹的数量Rc积累量增加;进行基于状态的维修、事后维修的作用是使积累的退化状态的导弹数量D和故障状态的导弹的数量F减少。
装备的可用度是战备完好性衡量的一个重要指标[9]。战备正常状态的装备的假定是指在前次执行任务中,若装备没有发生故障,处于正常状态,可以按要求再执行下次任务;若装备发生了故障,而维修时间只要不超过再次执行任务前的间隙时间,则不影响再次执行一个任务,装备也处于正常状态[10]。因此在模型中,若发现存在潜在故障状态的导弹在进行基于状态的维修,主要是进行换件维修和调试,维修时间相对比较短,相比起事后维修的导弹的时间间隔,几乎可以忽略不计,可以认为导弹是可用的。因此,进行基于状态维修的导弹视为可用状态的导弹,令可用导弹为U,则得到U的方程为
U(t)=R(t)+D(t)+Rc(t)+Rt(t)
(15)
4.4 系统的动态仿真运行分析
通过对基于CBM的导弹保障体系的建模,可以在系统动力学仿真软件Vensim PLE中运行模型。对模型进行基于状态的维修的比例系数进行灵敏度分析,从而确定基于状态的维修的影响程度。本模型中,以某保障大队潜射导弹维修保障情况为研究对象,假设所考察集合内有100枚导弹,设定所调整的基于状态的维修比例系数k1=0,k2=0.25,k3=0.5和k4=0.75进行仿真。仿真结果如图8~图11所示。(由于保密要求,对部分仿真参数进行修改)

图8 正常状态的导弹
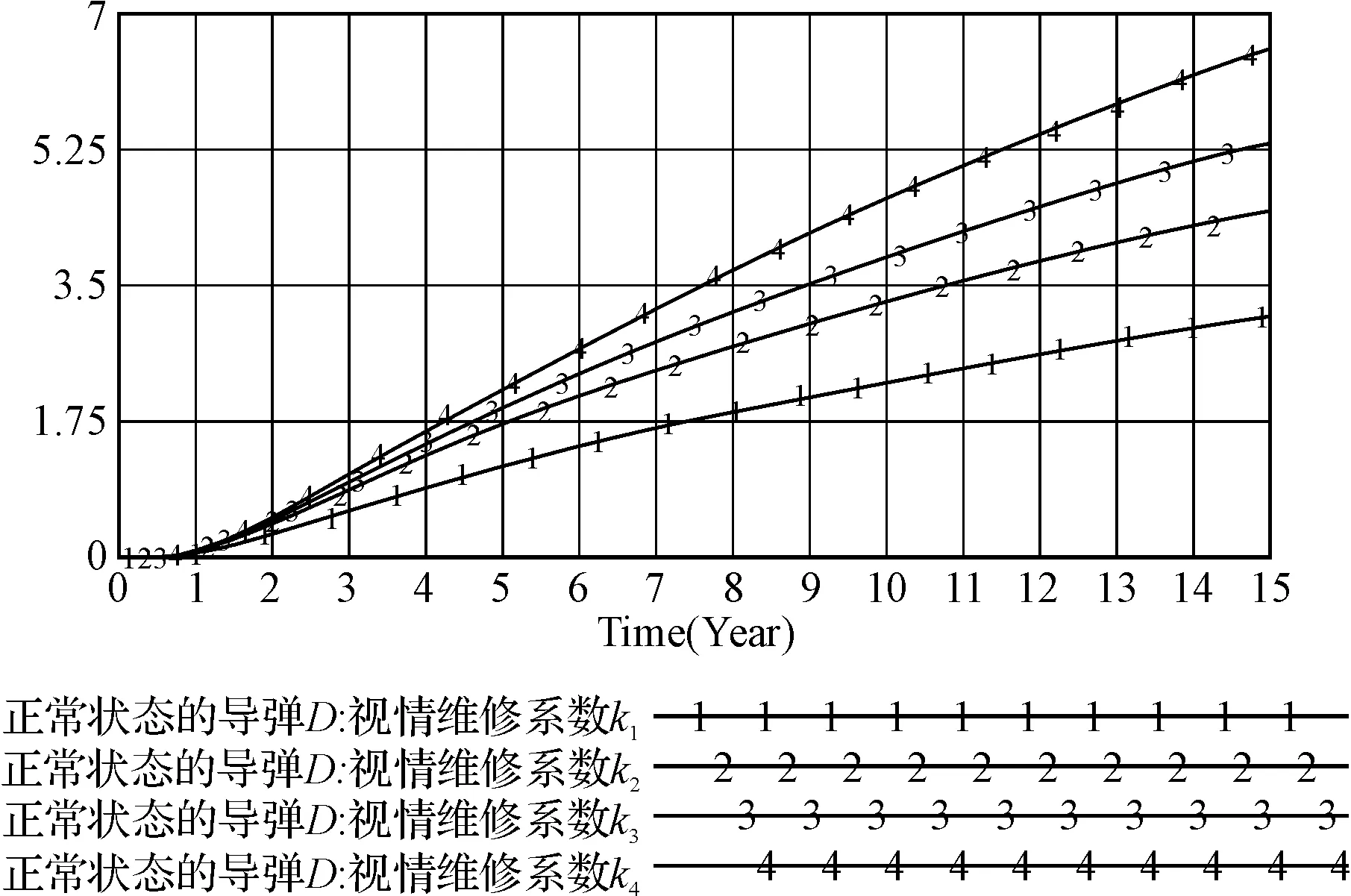
图9 退化状态的导弹

图10 故障状态的导弹

图11 可用状态的导弹
根据系统动力学理论,系统动力学模型对参数变化具有不敏感性和鲁棒性。图8~图11中的仿真曲线因基于状态的维修比例系数的取值的不同而存在细微差别,但并没有改变曲线趋势,仿真曲线的相似性证明了该仿真模型的鲁棒性,符合系统动力模型对参数变化相对不敏感的要求。
由图8可看出,在第3年以前导弹基本上都处于正常状态,未出现退化现象。当到了第10年,k=0与k=0.75时的正常状态的导弹数量相差到了8枚,到15年时相差到了12枚。图9~图10可以看出退化和故障状态的导弹随着时间的推移都逐渐增加,但随着系统k的增加,曲线逐渐趋于平稳且第一枚退化状态的导弹和故障状态的导弹出现的时间也越来越晚。由图11可以看出,当到10年时,k=0时可用状态的导弹在为90枚左右,其中正常状态的导弹为82枚左右,能勉强满足基层部队的战备完好率的需求,其结果基本上符合现实情况。而当k=0.75时,可用状态的导弹能维持在95枚左右,其中可用状态的导弹数量为90枚左右,可以很好地保证战备完好率。
5 结语
本文通过基于状态的维修导弹保障系统的研究,依据系统动力学理论,建立其系统动力学模型,借助某型导弹的维修情况的统计数据,进行了仿真。仿真结果有力地揭示了基于状态的维修可以有效地提高正常状态和可用状态的导弹的数量,并有效的减少退化状态、故障状态的导弹的数量,增强部队导弹装备的战备完好性,降低装备的维修保障费用,具有重要的现实意义和军事经济效益。
[1] 蒋兵兵,刘勇志,马亮.增强型基于状态的维修应用探讨[J],舰船科学技术,2013,35(9).139-142.
[2] 尹晓虎,温熙森,钱彦岭,等.复杂维修系统的动力学行为仿真田[J]兵工学报,2008,29(5):588-591.
[3] 王广伟.发动机滑油信息综合与面向任务维修决策[D].长沙:国防科技大学工学硕士学位论文,2002.
[4] Marcus Bengtsson. Condition Based Maintenance System Technology-Where is Development Heading[C]//Proceeding of the 17thEuropean Maintenance Congress, Barcelona,2004:580-588.
[5] 莫布雷J.以可靠性为中心的维修[M].北京:机械工业出版社,1995.
[6] 王其藩.系统动力学[M].北京:清华大学出版社,1994.
[7] 胡军燕,朱桂龙,马莹莹.开放式创新下产学研合作影响因索的系统动力学分析[J].科学学与科学技术管,2011,32:49-37.
[8] 秦颖博.基于SD模型的陕西电子及通信设备制造业创新系统研究[D].西安:西安工程大学硕士学位论文,2011.
[9] 宋太亮.装备综合保障实施指南[M].北京:国防工业出版社,2004.
[10] 李院生.时和平,装备战备完好性及其影响因素分析[J].电子产品可靠性与环境试验,2007,25(1):38-41.
Effectiveness Analysis of Condition-based Maintenance in the Missile Support
CHEN Zhaoming1MA Liang1XU Yang2
(1. Navy Submarine Academy, Qingdao 266000)(2. No. 91880 Troops of PLA, Jiaozhou 266300)
The missile maintenance support system is a complex nonlinear system. The method of system dynamics simulation can clearly express the relationship between system elements, and effectively develop a simulation for such a complex maintenance support system. The dynamic model of the maintenance behavior characteristics is obtained by analyzing the missile maintenance support the relationship between system elements in this paper. Finally, the experiment result validates that condition based maintenance has a distinct advantage for improving the effectiveness of missile support.
condition based maintenance, system dynamics, missile
2015年1月7日,
2015年3月2日 作者简介:陈兆铭,男,硕士,助理工程师,研究方向:武器装备管理与技术保障。
E920
10.3969/j.issn1672-9730.2015.07.039
