基于OpenGL的实时三维海浪可视化仿真

沈祉怡 赵冰化 张晓蕾

(1.92941部队 葫芦岛 125001)(2.95890部队 武汉 430030)(3.中国南方航空湖北分公司 武汉 430000)



基于OpenGL的实时三维海浪可视化仿真

沈祉怡1赵冰化2张晓蕾3

(1.92941部队 葫芦岛 125001)(2.95890部队 武汉 430030)(3.中国南方航空湖北分公司 武汉 430000)

海浪虚拟仿真技术是海上虚拟作战平台模型库构建的重要组成,直接影响到平台运行的逼真性和可行性。论文首先以重力波为例,分析了对规则海浪模型的仿真方法,然后采用线性波浪叠加法和海浪谱理论,探讨了不规则海浪模拟及其三维生成算法,通过建立海面规则网格,调用OpenGL函数库,实现了对真实海浪进行模拟,为建立海上虚拟作战平台海浪模型提供了一种技术方案。

不规则波浪; 海浪谱; 实时仿真; OpenGL

Class Number TP391

1 引言

海上虚拟作战平台需要构建诸多模型库,关于海浪的建模和实时三维动态仿真是其中一个重要研究课题。海浪模拟作为计算机仿真模拟的热点和难点之一,一直以来都受到人们广泛关注。真实的海浪是一种复杂的随机过程,无论时间还是空间上,都具有不规则性和不重复性[1]。国内外许多学者对此进行了大量研究,归纳起来目前在海浪仿真领域比较常用的几种方法有:基于几何造型的方法、基于物理量模型的方法、基于海浪谱的方法和基于Perlin噪声的方法。

基于海浪谱的方法利用多年来的海洋学观测结果,无需解复杂的动力学方程就能生成较真实的海浪,20世纪50年代初,Pierson[2]最先将Rice关于无线电噪声的理论应用于海浪,从此利用谱以随机过程描述海浪成为主要的研究途径,至今已提出多种海浪谱,如Pierson-Moscowitz[2]、JOSWAP[3]、Bretschneider、Wallops和TMA谱等[4]。Mastin[5]采用Pierson-Moscowitz谱合成不同振幅和相位的正弦波来仿真海面。Premoze等[6]采用JOSWAP谱,运用与Mastin相似的方法,得到了真实感较强的海面仿真效果,Cieutat等[7]又对其进行了改进,并将水波产生的力应用到船模型上,实现了一个舰艇模拟训练器。

Tessendorf和Jensen[8]等分别借鉴海洋经验模型和统计模型,对大量正弦波进行叠加,然后通过快速傅里叶变换(FFT)模拟海浪。Tessendorf的方法被很好地应用到了“水世界”和“泰坦尼克号”两部电影中。王胜正[9]把海浪高度作为一个独立变量,时间t时,点x的高度记作h(x,t),x表示地平线上某一点,记作x=x(x,z)。后来他又对该方法进行了改进。尹勇、徐利明等[10]采用基于浪级划分和海浪谱模拟海浪。Thon[11]综合采用摆线(trochoid)和谱分析方法模拟平静的水面。

综合国内外的研究现状以及目前海上虚拟作战平台对于海浪模型的需求,研究其实时三维动态仿真有着重大的技术价值和现实意义。本文首先以重力波为例,分析并实现了对规则海浪模型的仿真,然后采用线性波浪叠加法和海浪谱理论,探讨了不规则海浪模型及其三维生成算法,并调用OpenGL函数库实现了对真实海浪的模拟。

2 重力波的数学模型及仿真

2.1 重力波的数学模型分析

首先研究规则的海浪模型,以经常观测到的重力波为例,它通常是由水面的风力引起的。关于重力波,可以设定为一个初始时刻呈指数分布的流体高度扰动,在重力作用下的波动自由传播过程。流体高度的初始分布函数为

(1)

其中,x0和d分别为扰动中心位置和扰动波幅的半宽。流体在重力作用下开始运动,形成重力波并以圆形向各个方向传播。根据式(1),重力波满足平面上一维浅水波方程的特征。对于一维浅水波方程(u和h是流体流速和深度,g为重力加速度):

(2)

在t时刻,重力波形如图1中波1所示,在(t+Δt)时刻,波形如图1中波2所示,在H平面的一个波长水域为单位圆环域,自由表面映射成单位圆,底部边界映射成(r=r0)和(r+Δr)=(r0+Δr)=(r0+u*Δt)的两个圆。波形传播示意图如图1所示。由(1～2)及图1可以解出,在任意一点(x,y,h)处,各个变量之间的关系:

(3)

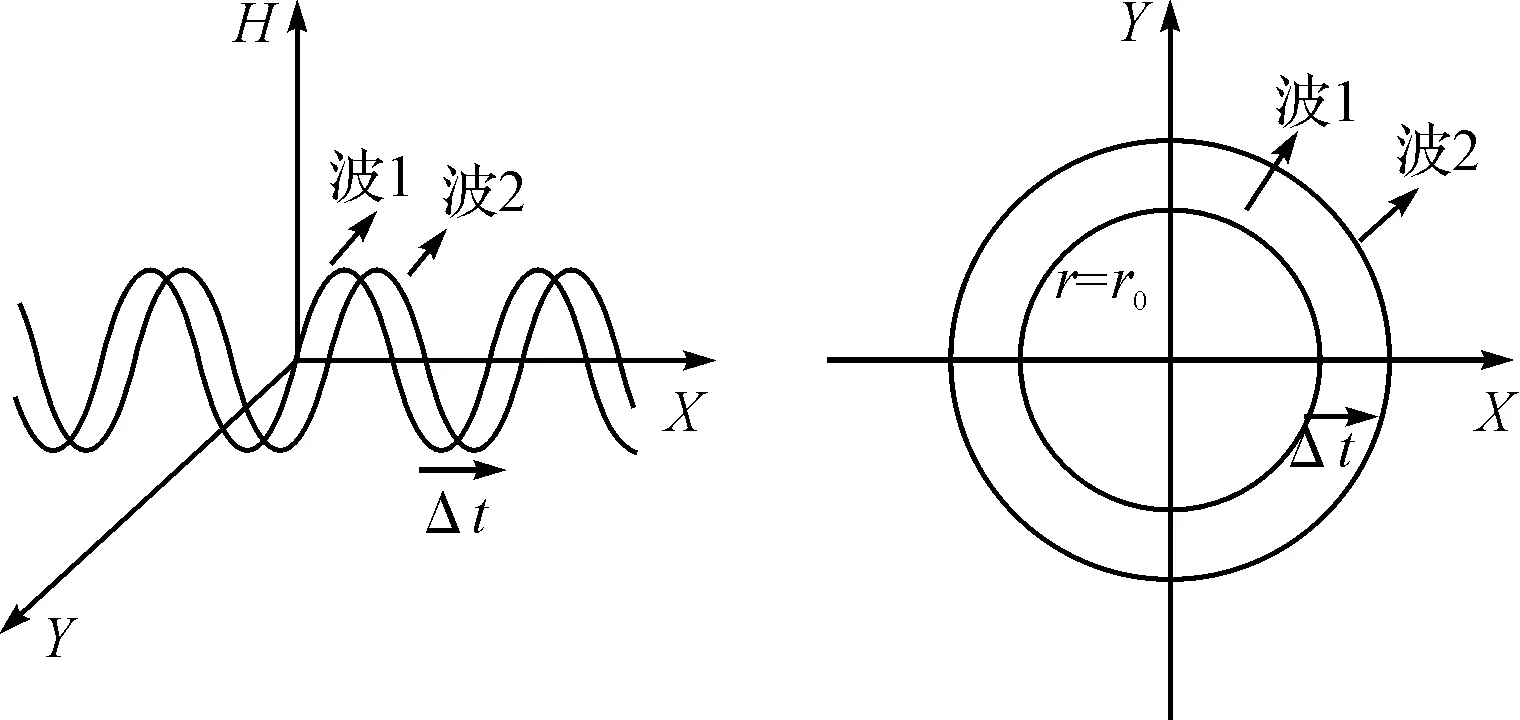
图1 重力波传播映射波形

2.2 基于OpenGL的重力波仿真

对重力波进行模拟,首先令波速u=-4,波长A=2,PI=3.14159,初始相位w=0,相位增幅Δw=0.1,则最初的波形(t=t0)的主要代码如下:

wave[x][y] = 2*sin((float)x*180/PI); w[x][y]=0;

在(t=t0+Δt)时刻,波形的主要代码如下:

s = sqrt((x-dx)*(x-dx) + (y-dy)*(y-dy)); w[x][y] += △w;

t = s/u; wave[x][y] = A*sin(2*PI *(w[x][y]+t));

在PC机器(CPU为双核Intel(R) T5670,内存2M,GForce 9300显卡)运行效果截图如图2所示,运行环境为Visual Studio 2008 + OpenGL 2.1库。

图2 重力波模拟

3 基于波浪谱的数学模型分析

3.1 P-M海浪谱分析

海浪谱是海浪变化的重要统计性质,它代表了固定点海浪波能量相对于频率的分布,对于描述海浪运动具有十分重要的意义。目前已提出的海浪谱主要以风向和浪能量等要素作为参数。换而言之,基于海浪谱的海浪模型能够交互地调节风向、海浪能量等参数。由于与风向相关的海浪波动理论仍有许多至今无法解决的问题,所以从理论上导出海浪谱是十分困难的,海浪谱主要通过长期观察得到。

目前常用的海浪谱有P-M谱、Phillips谱、B-M谱等。本文将基于P-M谱构建基本的海浪模型,其谱公式如下(式中,a=8.1×10-3;β=0.74;ag2=0.78):

(4)

(5)

3.2 不规则海浪数学模型分析

对于充分发展的海浪,其统计特性是稳定的,不随时间改变,因此可以将这时的海浪作为一个平稳随机过程来研究。海浪可由多个(理论上因为无限多个)不同周期和不同随即初相位的余弦波叠加而成,公式如式(6):

×cos(kixcosθj+kiysinθj-ωit+εij)

(6)

式中,η(x,y,t)为固定点(x,y)处的波动水面相对于静止水面在t时刻的瞬时高度;ωi和ki为第i个组成波的圆频率和波数;t分别为海浪运动的时间;εij为第i个组成波的初始相位,此处取为(0,2π)中的随机变量。S(ωi,θj)为方向谱,一般写成如下形式:

S(ωi,θj)=S(ω)G(ω,θ)

(7)

Δω=(ωH-ωL)/M

(8)

3.3 基于OpenGL的不规则海浪模拟

对不规则海浪进行模拟,首先令波长A=0.15+0.05*t,PI=3.14,第i个组成波的初始相位εij,相位增幅Δw=0.1,则海浪波形仿真的具体过程如下。

3.3.1 海浪数学仿真

首先定义一个随机变量εij:

float e = 0 + rand()%6.28;

樱桃番茄播种适期是根据当地终霜期早晚、栽培品种与目的、苗床以及分苗次数等情况来确定。一般春季露地栽培，以当地终霜期往前推算60～70天为适宜播种日期。可利用阳畦、温床、温室等设施育苗。播前应进行种子处理，多实行普通的温汤浸种，或采用药剂浸种。将浸过的种子放在25～30℃的环境下，2～3天即可出芽。选晴天上午播种，先浇底水后再播，可撒播，播种要均匀，覆土厚度不超过1厘米。利用营养钵和育苗盘育苗的，先将容器装满营养土，整齐的摆放在畦内，然后浇透水，每穴播2～3粒种子，播种后覆土，然后加盖地膜或小拱棚，以利增温和保湿。

其次选取合适的采样间隔,建立海面规则网格,通过网格点的水平坐标(x,y)和时间来反演出该点点额波高。为仿真简单起见,令波长为一递增随机变量,则海浪的模拟仿真代码如下:

for (A=0.05;A<5;A=A+0.05)

{

water[i][j] = A *r *cos(10.0 * ( (i + 0.1 * j) / Meshsize) * 2.0 * 3.14 *(wt[i][j]+t)) + e

}

3.3.2 定义观察点和光源

gluLookAt参数可以设置观察点的位置,它的参数比较多,前三个参数表示了观察点的位置,中间三个参数表示了观察目标的位置,最后三个参数代表从(0,0,0)到(x,y,z)的直线,它表示了观察者认为的“上”方向。sun_light_XX定义了太阳光源,它是一种白色的光源。

gluLookAt(10.0, 50.0, -100.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0);

GLfloat sun_light_position[] = {0.0f, 0.0f, 5.0f, 1.0f};

GLfloat sun_light_ambient[] = {1.0f, 1.0f, 1.0f, 1.0f};

GLfloat sun_light_diffuse[] = {1.0f, 1.0f, 1.0f, 1.0f};

GLfloat sun_light_specular[] = {1.0f, 1.0f, 1.0f, 1.0f};

3.3.3 仿真结果

在PC机器(CPU为双核Intel(R) T5670,内存2M,Gforce 9300显卡)运行效果截图如图3所示,运行环境为Visual Stidio 2008 + OpenGL 2.1库。

图3 不规则波模拟

由于可见性判断会同时考虑视见体的六个面,算法相当复杂,因为本文在纹理映射和网格视点可见性方面,仍需要有改进的空间。

该方法简单直观,实时性相对较好,可适用于对真实性要求不是很高的情况。但由于采用规则矩形粗网格,进行实时绘制时要避免FFT方法产生的视觉重复性,因此降低了仿真的质量和真实感。

4 结语

本文首先以重力波为例,分析并实现了对规则海浪模型的仿真,然后采用线性波浪叠加法和海浪谱理论,探讨了不规则海浪模型及其三维生成算法,并调用OpenGL函数库实现了对真实海浪的模拟,仿真在实时性与真实感方面均取得了较好的效果,为建立海上虚拟作战平台海浪模型提供了一种可行的技术方案。

[1] 潘玉田,马新谋,杨栋.三维随机波浪的数值仿真研究[J].火炮发射与控制学报,2010(3):5-8.

[2] Pierson W J, Moskowitz L. A Proposed Spectral Form for Fully Developed Wind Seas Based on the Similarity Theory of S. A. Kitaigorodskii[J]. Journal of Geophysical Research,1964,69(24):5181-5190.

[3] 肖维超.海浪绘制及仿真技术研究[D].哈尔滨:哈尔滨工程大学,2009:12-31.

[4] 解翠,金一丞,李志华,等.改进的实时海浪网格模型[J].系统仿真学报,2004,16(10):2146-2148.

[5] Mastin G A, Watterberg P A, Mareda J F. Fourier synthesis of ocean scenes[J]. IEEE Computer Graphics and Applications,1987,7(3):16-23.

[6] Premoze S, Ashikhmin M. Rendering natural waters[J]. Compurer Graphics Forum,2001,20(4):189-200.

[7] Cieutat J M, Gonzato J C, Guitton P. A general ocean waves model for ship design[C]//Proc. of Virtual Concept Conference, France: Biarritz,2003:187-194.

[8] Tessendorf J. Simulating ocean water[J]. Simulating Nature: Realistic and Interactive Techniques. SIGGRAPH,2001:4-16.

[9] 王胜正,关克平,徐铁.航海视景仿真的海浪生成算法[J].上海海事大学学报,2005,26(1):16-18.

[10] Yin Y, Jin Y C, Ren H X. Wave simulation of visual system in marine simulator based on wave spectrums[C]//Proc. of MARSIM’03, Japan: Kanazawa,2003:288-294.

[11] Thon S, Dischler J M, Ghazanfarpour D. Ocean waves synthesis using a spectrum-based turbulence function[C]//Computer Graphics International,2000:65-72.

Real-time Visualization of Three-dimensional Simulation of the Waves Based on OpenGL

SHEN Zhiyi1ZHAO Binghua2ZHANG Xiaolei3

(1. No. 92941 Troops of PLA, Huludao 125001)(2. No. 95890 Troops of PLA, Wuhan 430030) (3. Hubei Branch of China Southern Airlines, Wuhan 430000)

The key technology of wave simulation is an important part of marine virtual combat platforms. It directly affects the fidelity and feasibility. Firstly, the mathematical model and simulation of gravitational waves is analyzed and completed OpenGL-based gravity wave simulation. Then the mathematical model based on wave spectrum is studied, including P-M wave spectrum analysis and mathematical model of irregular waves. Finally, the OpenGL-based simulation of irregular waves is completed.

irregular waves, wave spectrum, real-time simulation, OpenGL

2015年1月17日,

2015年2月27日 作者简介:沈祉怡,女,助理工程师,研究方向:指挥自动化及三维模拟仿真。赵冰化,女,讲师,研究方向:信息系统与智能决策。张晓蕾,女,工程师,研究方向:计算机应用、航空电子。

TP391

10.3969/j.issn1672-9730.2015.07.033