基于有限元和模态法的轮轨动力对比分析

米 洋，刘永孝

（兰州交通大学 土木工程学院，甘肃 兰州730070）

众所周知，现代铁路交通运输事业发展迅速，特别是列车运行速度、运载重量和运输密度的大幅度提高，使得铁路车辆和轨道系统动力学的问题更加突出，也更趋复杂。列车行车速度越高，车辆与轨道之间的动态相互作用越强。因此，车辆－轨道耦合动力学的研究刻不容缓。

近十年来，国内外关于轮轨相互作用的研究十分活跃，建立了各种繁简不一的模型，从转向架－轨道双层分布参数模型，到整车—轨道相互作用模型。最终，在国内基本确定了两种不同的建模思想:有限元法和模态法。与此同时，国内许多学者也对这两种方法进行了不同深度地研究。文献［2－3］利用有限元的方法，建立了车辆－轨道耦合系统动力学模型，讨论了轨道高低随机不平顺对系统的影响。文献［4］从模态法的角度另辟蹊径，分析了轨道高低不平顺下轮轨垂向接触的动态关系。文献［5］采用周期图法估计出车辆－轨道垂向和横向随机响应功率谱密度PSD，并进行谱分析。最终得到其随机振动的基本规律。文献［6］概括地介绍了模态法的研究现状和进一步需要解决的问题。但是，国内学者很少对这两种方法进行比较，本文就分别用有限元法和模态法建模，对这两种方法所获得的轮轨动力特性进行比较，从而找出它们的特点。

1 模型的对比分析

1.1 有限元法和模态法的相同

1）有限元法和模态法均采用带有一系、二系悬挂刚度的整车模型，将钢轨看成连续弹性离散点支撑上的Euler梁。在钢轨下，分别把轨枕和路床进行离散，视作离散的轨枕块和道床块，其质量处理成为集中质量。下部结构均视作三层（钢轨—轨枕—道床—路基）弹簧－阻尼振动模型。该模型可以充分反映体系垂向的功能及其相互作用关系。轮轨接触部分均采用了Hertz非线性弹性接触理论，假设在车轮－轨道之间设置Hertz弹簧，以此起到联系上部车体和下部轨道系统的作用（如图1所示）。

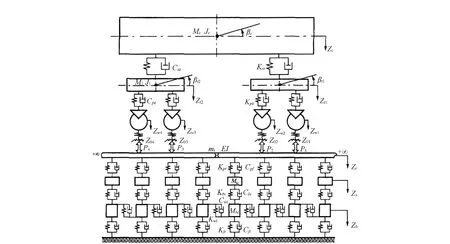
图1 车辆—轨道系统模型

2）由于研究的都是动力学问题，这两种方法都借鉴了Hamilton原理方程

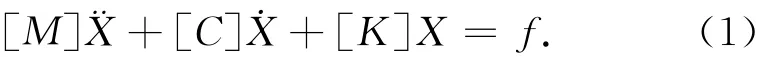
式中:［M］为广义质量矩阵，［C］为广义阻尼矩阵，［K］为广义刚度矩阵，f为广义荷载阵。

1.2 有限元法和模态法的不同

这两种方法在建模方面有着一个本质的不同点，有限单元法将钢轨分成了无数个单元，这些单元的左右两个节点是钢轨与轨枕的扣压点（即轨枕支撑点）。而模态法将钢轨视作一根连续长的梁，并不将其分解为无数个小单元，其利用Ritz法引入振形函数Yk（x）

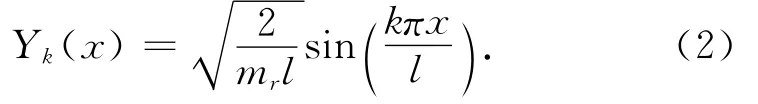
这是一个仅与模态阶数和位置变量有关的函数。同时令钢轨的竖向位移

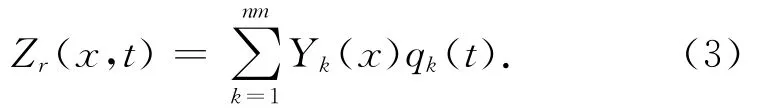
式中:qk（t）为钢轨正则振形坐标。

从该本质的不同点出发，研究发现这两种方法在计算过程中存在差别，在计算结果上具有些许差异。另外，二者在许多方面还有着不同。例如:模态法分析的物理模型充分考虑了道床离散块之间的横向剪切刚度Kw和阻尼Cw。但是有限元法却忽略了道床块之间的横向连接。本文针对这两种方法的不同，将其列入表1，以供读者比较。

表1 有限元法和模态法的比较

2 实例验证及分析

本文参考文献［7］和文献［3］分别列出车辆－轨道竖向耦合动力学的模态法和有限元法数学模型方程，采用文献［1］新型显示积分方法求解系统振动方程组，并利用Matlab软件编程实现，将两种计算结果画于一张图中进行比较。仿真计算文献［7］附录所提供的长春客车厂250km／h高速客车以160km／h的速度通过有砟轨道上美国6级轨道谱时的轮轨垂向作用力P，加速度A，速度V，位移X。

在有限元计算中，在钢轨上选取300个单元，一个节点有两个自由度，那么总共就有1 214个自由度。相反模态仿真过程中自由度仅有762，这是因为截止模态阶数取150，仅为钢轨上自由度604的四分之一。模态法的这个优势很明显的表现在了计算时间上，相比较有限元法32min的运行时间，模态法只用了18min，节省了将近一半。

为了进一步对两种方法进行比较，下面将计算的部分结果表示如图2所示。

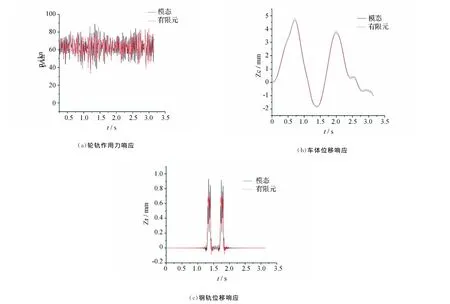
图2 部分计算结果

比较图2中轮轨作用力，车体位移和钢轨位移的时间响应曲线。显而易见的是，经过有限元法和模态法建立的方程并求解之后的结果是极为近似的，两者的图形几乎吻合。为了进一步证明这两种方法具有同样的结果，对采用不同方法计算所得的位移最大值进行比较。见表2。

表2 位移比较

在表2中轮轨作用力相差0.06kN，车体位移，钢轨位移和轨枕位移的差值都在0.2mm以内。由此可见，这两种方法在车辆－轨道垂向耦合动力学研究当中具有同等的效果。

在动力学分析中，相对于位移和速度而言，加速度是最具敏感性的。也就是说如果用两种方法分别计算的加速度时程响应曲线再次吻合，基本就可以说明两种方法是近似的。为了证明以上假设，系统各个部位的加速度时程响应曲线如图3所示。

图3中，用有限元法计算得出的加速度响应显然和模态法的计算结果趋于重合。用有限元法计算得出的车体加速度峰值，钢轨加速度峰值，轨枕加速度峰值和道床加速度最大值分别为0.1g、0.96 g、1.01g和 0.95g。这与模态法计算的结果:0.101g、1.43g、0.89g、0.65g 相 差 0.001g、0.47g、0.12g、0.30g。车体加速度最大值极为接近，但是钢轨，轨枕和道床的加速度却相差明显。

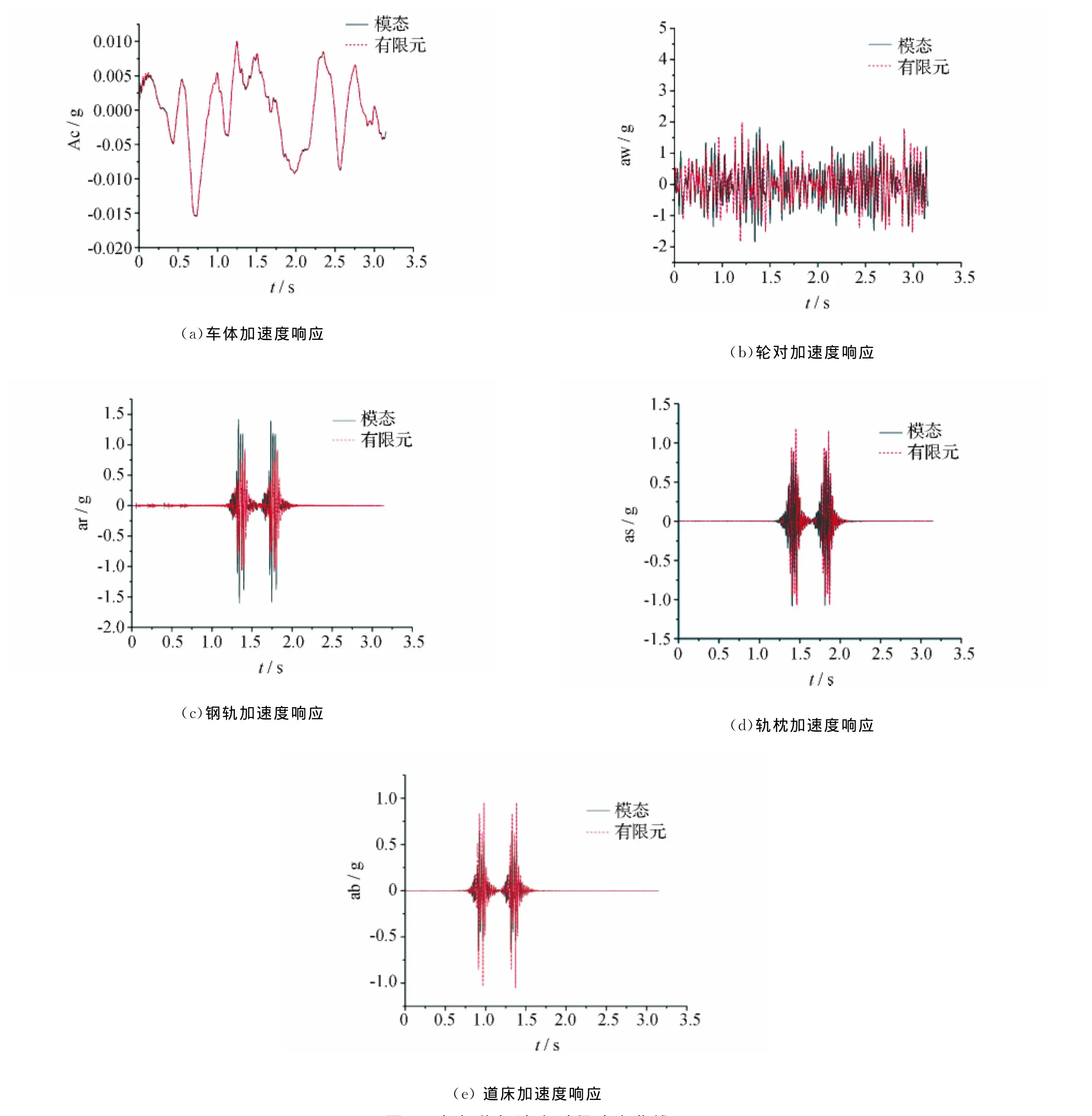
图3 各部位加速度时程响应曲线

正是由于有限单元法将钢轨从头到尾划分为许多个有限长单元，充分考虑了各个单元之间的相互影响，得到的在美国6级谱高低不平顺上的轮轨冲击效应比模态法仅将钢轨作为一条整体欧拉梁进行分析计算得出的结果更为明显，影响的轨道范围更广泛。这就是说，就求解结果而言，有限元法要比模态法更加精确。

3 结 论

通过本文对有限元法和模态法的比较，可以看出有限元法和模态法在解决车辆－轨道耦合动力学的建模方面是等效的，它们得出的结果具有相似性。但是，模态法由于自由度数较少，所以相比有限元法，计算速度更快。而有限元法由于充分考虑了单元之间的相互影响，并且单元的划分更加详细，所以有限元法要比模态法更加精确。

基于以上两种方法的特点，当系统的自由度数较少时，有限元法和模态法计算时间相差不多，但是有限元法计算结果更加精确，所以前者显然更加适用。随着钢轨长度的增加，自由度数的增多，这时模态法和有限元法的计算时间差会成倍的增多，模态法的优点将逐渐凸显出来。模态法此时明显更加方便。这将在我们日后的研究工作中提供参考。接下来，我们会对不同参数影响下两种方法的计算结果进行对比，以进一步对这两种方法的适用性进行界定。

［1］ 翟婉明.车辆－轨道耦合动力学［M］.3版.北京:科学出版社，2007:20－38.

［2］ 雷晓燕，毛利军.线路随机不平顺对车辆—轨道耦合系统动力响应分析［J］.中国铁道科学，2001（6）:39－44.

［3］ 毛利军，雷晓燕.车辆－轨道耦合系统随机振动分析［J］.华东交通大学学报，2001，18（2）:12－19.

［4］ 谢国伟.铁路车辆－轨道垂向耦合动力学仿真［D］.昆明:昆明理工大学，2013.

［5］ 陈果，翟婉明，左洪福.车辆－轨道耦合系统垂横模型及其验真［J］.振动与冲击，2001，20（4）:16－21.

［6］ 翟婉明.车辆－轨道耦合动力学研究的新进展［J］.中国铁道科学，2002（2）:1－11.

［7］ 陈果.车辆－轨道耦合系统随机振动分析［D］.成都:西南交通大学，2000.

［8］ Chunlei Yang，Fu Li，Yunhua Huang，et al.Comparative study on wheel–rail dynamic interactions of sideframe cross－bracing bogie and sub－frame radial bogie［J］.Journal of Modern Transportation，2013，21（1）:1－8.

［9］ Linya Liu，Bin Zhang，Jin Wang.Rail dynamic vibration absorber design and vibration reduction analysis［J］.Noise ＆ Vibration Worldwide，2011，42（11）:2－7.

［10］张安琳，蒲泽旭，王敏，等.京津城际高速铁路对区域社会经济影响分析［J］.交通科技与经济，2013，15（1）:14－18.