希尔伯特空间中关于保持距离的Aleksandrov问题

2015-03-10郑风华任卫云

哈尔滨商业大学学报（自然科学版） 2015年3期

关键词：希尔伯特等距风华

郑风华，任卫云

(天津大学理学院，天津300072)

希尔伯特空间中关于保持距离的Aleksandrov问题

郑风华，任卫云

(天津大学理学院，天津300072)

设X和Y是希尔伯特空间，T：X→Y为一映射，证明了若T保1和另外一个实数，则T是一个线性变换，从而部分解决了Aleksandrov问题.

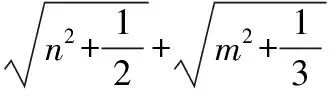
1970年，A·D·Aleksandrov提出：若T为定义在两个距离空间中的映射，是否由f保某一个距离能够得出其为一个等距映射？此即所谓的Aleksandrov问题.该问题被许多数学工作者广泛的研究并且已经得到了一些结果.然而圆满地解决Aleksandrov问题尚且具有一定的难度，一些数学工作者开始考虑另外一个问题: 如赋范空间中的映射保两个距离，是否必为等距的？针对这一问题，W·benz在文献中证明了定理令X和Y是实赋范空间，假设X的维数大于等于2，Y是严格凸的，如果T:X→Y满足下列两个条件：

1)对于X的任意两个元素x，y,若‖x-y‖=ρ，则‖T(x)-T(y)‖≤ρ；

2)对于X的任意两个元素x,y，若‖x-y‖=λρ，则‖T(x)-T(y)‖≥λρ；

则T是一个仿射等距变换.

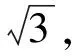
定义1设X和Y是距离空间，T:X→Y为一映射，若对X的任意两个元素x，y,当dX(x,y)=1时有dY(T(x),T(y))=1，则称T为保距离1的，简称保1的，若对X的任意两个元素x，y,有dY(T(x),T(y))则称T为等距的.

引理令X和Y是实赋范空间，如果T:X→Y保“1”，对于X的任意两个元素x，y,若‖x-y‖=n，则‖T(x)-T(y)‖≤n.

证明：当n=1时，结论显然成立；

假若当n=k(k∈N*)时，结论仍成立，即：

‖T(x)-T(y)‖≤k；

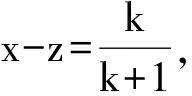
所以‖T(x)-T(y)‖≤‖T(x)-T(z)‖+

‖T(z)-T(y)‖≤k+1.

由此，上述结论对于任意的n∈N*均成立，引理得证.

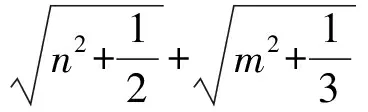
证明：

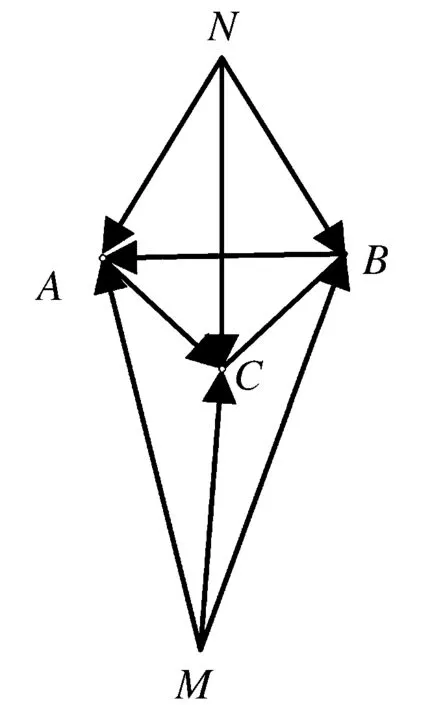
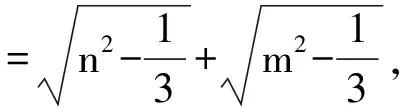
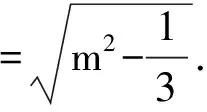
由引理得，‖T(N)-T(A)‖≤n,‖T(N)-T(B)‖≤n,‖T(N)-T(C)‖≤n

‖T(M)-T(A)‖≤m,‖T(M)-T(B)‖≤m,‖T(M)-T(C)‖≤m

令三角形T(A)T(B)T(C)的中心为O′，

x1=T(A)-T(C)，x2=T(B)-T(C)，y1=T(A)-T(N)，y2=T(B)-T(N)，y3=T(C)-T(N).

由T(B)-T(A)=y2-y1=x2-x1，

得1=〈y2-y1,y2-y1〉，〈y2,y2〉-2〈y1,y2〉+〈y1,y1〉≤2n2-2〈y1,y2〉, 1=〈x2-x1,y2-y1〉，〈x2,y2〉+〈x1,y1〉-〈x1,y2〉-〈x2,y2〉,

即-2〈y2,y2〉≤2n2-1，

〈x1,y2〉+〈x2,y2〉=〈x2,y2〉+〈x1,y1〉-1.

由y3=y2-x2=y-x1，‖y3‖≤n，

得〈y2-x2,y2-x2〉=〈y2,y2〉-2〈y2,x2〉+〈x2,x2〉≤n2，

〈y1-x1,y1-x1〉=〈y1,y1〉-2〈y1,x1〉+〈x1,x1〉≤n2，

即-2〈y2-x2〉≤n2-〈y2-x2〉-1，

-2〈y1-x1〉≤m2-〈y1-x1〉-1，

-〈x1+x2,y1+y2〉=-(〈x1-y1〉+〈x1-y1〉+〈x1-y1〉+〈x1-y2〉) =-(2〈x1-y1〉+2〈x1-y1〉-1) ≤2n2-〈y1,y1〉-〈y2-y2〉-1

〈x1+x2,x1+x2〉=〈x1，y1〉+〈x2，x2〉+2〈x1，x2〉=3

则‖T(N)-O′‖2

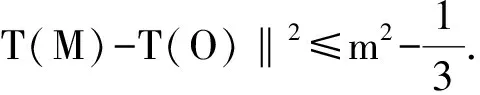
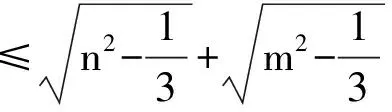
所以上边所得的不等式均为等式.

即‖T(N)-T(A)‖=‖T(N)-T(B)‖=

‖T(N)-T(C)‖=n

‖T(M)-T(A)‖=‖T(M)-T(B)‖=

‖T(M)-T(C)‖=m

这样我们就能得出T保1和n.

由定理1得，T是仿射等距变换.

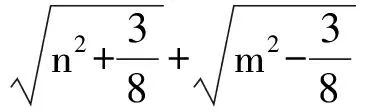
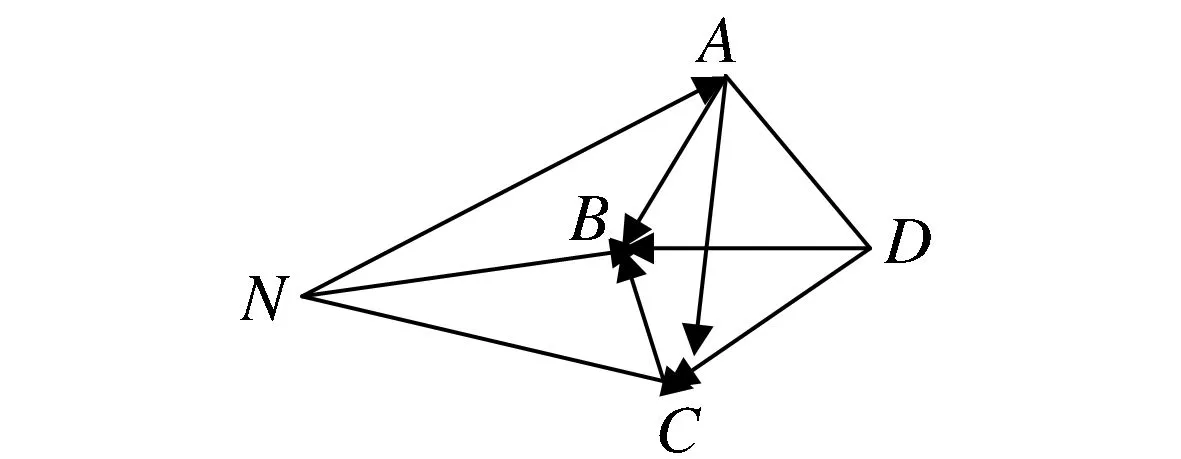
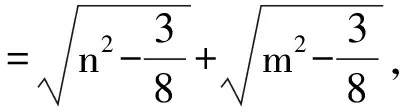
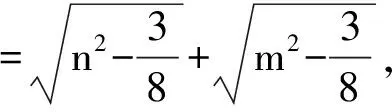
由引理得，

‖T(N)-T(A)‖≤n，‖T(N)-T(B)‖≤n，

‖T(N)-T(C)‖≤n，‖T(N)-T(D)‖≤n，

‖T(M)-T(A)‖≤n，‖T(M)-T(B)‖≤n，

‖T(M)-T(C)‖≤n，‖T(M)-T(D)‖≤n.

令正四面体T(A)T(B)T(C)T(D)的中心为O′，x1=T(B)-T(D)，x2=T(C)-T(D)，x3=T(B)-T(A)x4=T(C)-T(A)y1=T(B)-T(N)，y2=T(C)-T(N)，y3=T(A)-T(N).

由T(B)-T(C)=y1-y2=x1-x2=x3-x4，

得1=〈y1-y2,y1-y2〉=〈y2,y2〉-2〈y1，y2〉+〈y1,y1〉≤2n2-2〈y1-y2〉,

1=〈x1-x2,y1-y2〉=〈x2,y2〉-〈x1，y1〉+〈x1,y2〉-〈x2，y1〉,

1=〈x3-x4,y1-y2〉=〈x3,y1〉-〈x4，y2〉+〈x4,y1〉-〈x3，y2〉,

1=〈x1-x2,x3-x4〉=〈x1,x3〉+〈x2，y4〉+〈x1,x4〉-〈x2，x3〉,

1=〈x1-x2,x1-x2〉=〈x1,x1〉-2〈x1，x2〉+〈x2,x2〉,

1=〈x3-x4,x3-x4〉=〈x3,x3〉-2〈x3,x4〉+〈x4,x4〉,

即 -2〈y1,y2〉≤2n2-1.

〈x1,y2〉+〈x2,y1〉=〈x2,y2〉+〈x1,y2〉-1

〈x4,y1〉+〈x3,y2〉=〈x3,y1〉+〈x4,y2〉-1

〈x1,y4〉+〈x2,x3〉=〈x1,x3〉+〈x2,x4〉-1

由T(A)-T(D)=x1-x3=x2-x4,

得

1=〈x1-x3,x1-x3〉=〈x1,x1〉-2〈x1,x3〉+〈x3,x3〉

1=〈x2-x4,x2-x4〉=〈x2,x2〉-2〈x2,x4〉+〈x4,x4〉

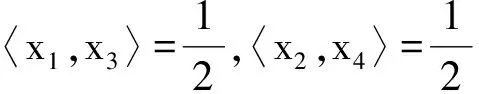
由 T(D)-T(N)=y2-x2=y1-x1，

得〈y2-x2,y2-x2〉=〈y2,y2〉-2〈y2,x2〉+〈x2,x2〉≤n2

〈y1-x1,y1-x1〉=〈y1,y1〉-2〈y1,x1〉+〈x1,x1〉≤n2

即 -2〈y2,x2〉≤n2-〈y2,y2〉-1

-2〈y1,x1〉≤n2-〈y1,y1〉-1

-〈x2+x2,y1+y2〉=-(〈x1,y1〉+〈x1,y2〉+〈x2,y1〉+〈x2,y2〉)

=-(2〈x1,y1〉+2〈x1,y1〉-1)

≤2n2-〈y1,y1〉-〈y2,y2〉-1

由T(A)-T(N)=y2-x4=y1-x3，

〈y2-x4,y2-x4〉=〈y2,y2〉-2〈y2,x4〉+〈x4,x4〉≤n2，

〈y1-x3,y1-x3〉=〈y1,y1〉-2〈y1,x3〉+〈x3,x3〉≤n2，

即 -2〈y2,x4〉≤n2-〈y2,y2〉-1

-2〈y1,x3〉≤n2-〈y1,y1〉-1，

-〈x3+x4,y1+y2〉=-(〈x3,y1〉+〈x3,y2〉+〈x4,y1〉+〈x4,y2〉)

=-(2〈x3,y1〉+2〈x4,y2〉-1)

≤2n2-〈y1,y1〉-〈y2,y2〉-1

〈x1+x2,x1+x2〉=〈x1,x1〉+〈x2,x2〉+2〈x1,x2〉=3

〈x3+x4,x3+x4〉=〈x3,x3〉+〈x4,x4〉+2〈x3,x4〉=3

〈x1+x2,x3+x4〉=〈x1,x3〉+〈x1,x4〉+〈x2,x3〉+〈x2,x4〉=2〈x1,x3〉+2+〈x2,x4〉-1=1

则‖T(N)-T(O)‖2

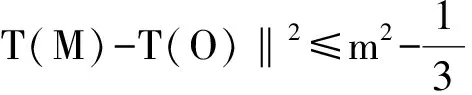
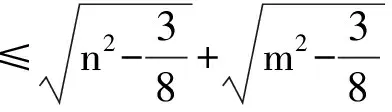
所以上边所得的不等式均为等式.

即‖T(N)-T(A)‖=‖T(N)-T(B)‖=‖T(N)-T(C)‖=n

‖T(M)-T(A)‖=‖T(M)-T(B)‖=‖T(M)-T(C)‖=m

这样我们就能得出T保1和n.

由定理得，T是仿射等距变换.

[1]BENZW,BERENSB.AcontributiontoatheoremofUlalnandMazur[J].AeqMath, 1987, 34: 61-63.

[2]XIANGSH.MappingsofConservativeDistancesandtheMazur-UlamTheorem[J].JournalofMathematicalAnalysisandApplications, 2001,254: 262-274.

[3]RENWY.OntheAleksandrovproblemin2-normedlinearspace[J].AcaScientiarumNaturaliumUniversitatisNankaiensis, 2008,41: 52-56.

[4]RENWY.OnConservativeMappingsofAleksandrovproblem[J].JofMathreserchandexposition, 2007(27): 613-616.

Study on conservative mappings of Aleksandrov problem in Hilbert space

ZHENG Feng-hua, REN Wei-yun

(School of Science, Tianjin University, Tianjin 300072, China)

LetX,Ybe Hilbert space andT:X→Ybe a mapping. This paper showed thatTwas a affine isometry ifTpreserves 1 and another postive real number, hence partly solved the Aleksandrov problem.