整体和浮置式道床隧道结构动应力计算分析

杨 宁 耿传智

整体和浮置式道床隧道结构动应力计算分析

杨 宁 耿传智

摘 要：利用ANSYS有限元软件，建立了整体道床和浮置板道床情况下隧道结构三维模型，通过对应实测轮轨力的输入，计算得到2种道床下隧道下层结构动应力的分布情况和大小。结论是，浮置板道床对于下层隧道结构动应力影响相较于整体道床小很多，且无论横向还是纵向动应力分布都更加均匀合理。从长远来看，钢弹簧浮置板轨道结构在满足减振降噪的功能前提下，可以有效减小轮轨力造成的隧道结构附加沉降。

关键词：地铁隧道；整体道床；浮置板道床；结构动应力；计算分析

中图分类号：U451

杨 宁：同济大学铁道与城市轨道交通研究院，硕士研究生，上海 201804

0　引言

随着盾构隧道使用年限的增加，列车循环荷载作用会引起隧道周边土体积累变形进而产生沉降，从长远看可产生50～80 mm的附加沉降。目前，国内地铁普遍采用整体道床结构和浮置板道床结构。浮置板道床具有良好的减振效果，减振效果可以达到20～40 dB。国内目前对这2种道床情况下隧道和土体的动应力分析尚无太多，而动应力分析对于研究列车引起的饱和软黏土地基附加沉降具有重要意义。本文应用有限元软件ANSYS，对浮置板道床和整体道床隧道在其他条件相同的情况下分别进行结构动应力模拟计算，荷载输入分别采用实测的浮置板道床轮轨力和整体道床轮轨力。

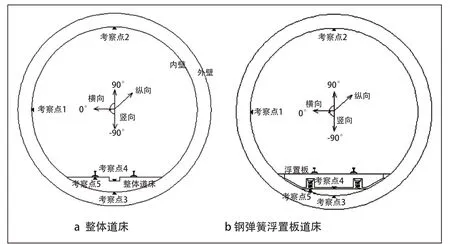
图1　隧道横断面及考察点示意图

1　计算模型

1.1隧道横截面形式

本文采用的2种道床对应的隧道横截面及考察点（计算点）如图1所示。整体道床横截面横向最大宽度为3 440 mm，最大高度为540 mm（不考虑排水通道）。浮置板道床截面横向最大宽度为3 540 mm，高度为450 mm。为实现浮置板道床与隧道衬砌内壁的连接，左右侧均采用22.54°的倾角设计，左右钢弹簧中心间距1 700 mm。

1.2三维计算模型

2种道床隧道内径均为3 m，衬砌厚度0.4 m，土体横截面尺寸采用20 m×20 m。2种道床和衬砌在横截面内采用0.1 m的单元大小进行划分，土体采用0.15 m单元大小进行划分，以保证足够的精度和尽可能少的单元数量。三维模型中衬砌结构、土体、整体道床及浮置板道床垫层均采用空间实体单元solid45，钢轨与道床的扣件连接沿纵向每隔0.6 m布置1个，浮置板钢弹簧和横向限位弹簧沿纵向每隔1.2 m布置1个。考虑到模型和施加荷载的对称性，选取整体模型的1/4对称部分进行分析，1/4模型的尺寸大小为10 m×20 m×15 m，其中浮置板道床采用短型浮置板，纵向长度为3.6 m（图2、3）。

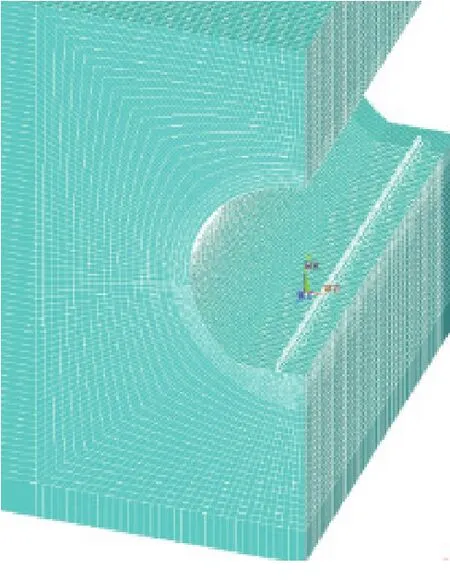
图2　整体道床三维隧道模型

图3　浮置板道床三维隧道模型

2　计算结果分析

2.1道床部分计算结果分析

2.1.1动应力云图分析

图4、5给出了整体道床和浮置板道床混凝土垫层动应力云图，通过对比图4、5以看出，由于浮置板钢弹簧本身起到了预先分散轮轨力的作用，使得浮置板道床混凝土垫层纵、横向受力相比于整体道床受力更加均匀，并没有出现较为集中的压应力。整体道床最大动应力为1 600 kPa，最小动应力则为179 kPa左右；而浮置板道床混凝土垫层最大动应力有1 280 kPa，最小动应力则为142 kPa。

2.1.2道床考察点动应力分布规律图6～8给出了道床考察点应力分布规律。

(1）由图6可知，在考察点4位置，整体道床的动应力沿横向分布规律是，在-0.7 m处（钢轨加载点位置）动应力出现峰值，其值为1 600 kPa，在尖峰范围的左右两侧动应力峰值变化很平缓；浮置板道床混凝土垫层的动应力分布规律则是，在加载位置左侧呈现线性衰减，动应力大小从1 000 kPa衰减到700 kPa。

(2）由图7可知，在考察点4位置，浮置板道床混凝土垫层的动应力沿纵向分布规律是，整体呈现出波浪形渐次衰减的趋势，在加载点位置附近、距离加载点2、5、8 m附近分别有峰值出现，峰值大小分别为1 050、600、150 kPa和50 kPa；整体道床的动应力分布规律则是，整体依然呈现波浪形渐次衰减的规律，但是相比更加平缓，未出现明显的波峰波谷，动应力最大值为180 kPa。

(3）由图8可知，在考察点5位置，整体道床的动应力沿纵向分布规律是，整体依然呈现出波浪形渐次衰减的趋势，在距离加载点纵向0～0.75 m、0.75～1.5 m范围内分别有2个尖峰区间出现，动应力峰值大小分别为1 600 kPa和700 kPa，在1.5 m以外的范围动应力基本呈现缓慢的波浪形衰减；浮置板道床混凝土垫层的动应力分布规律则是，整体依然呈现波浪形渐次衰减的规律，在距离加载点纵向0～0.75 m、0.75～2 m、1.5～4 m、4～7 m范围内分别有4个峰值区间出现，峰值大小分别为900、700、500 kPa和150 kPa。

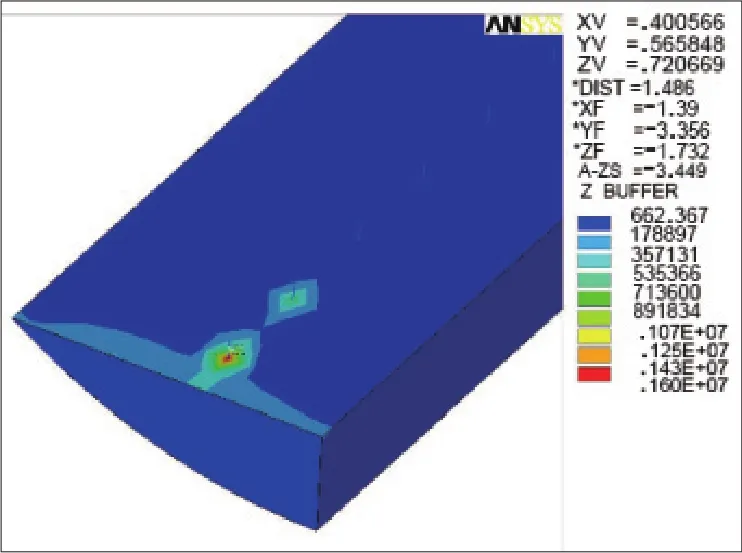
图4　整体道床动应力云图 （单位：Pa）

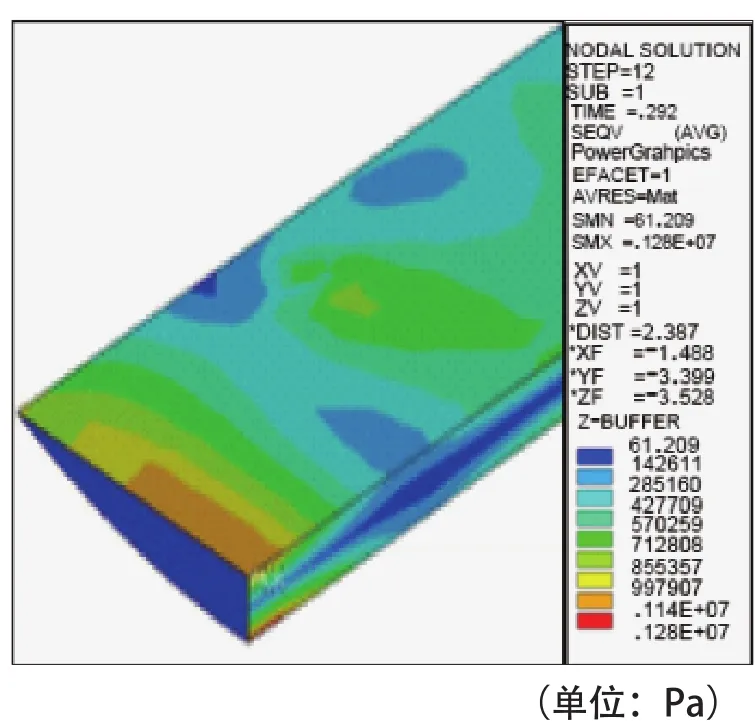
图5　浮置板道床混凝土垫层动应力云图

(4）通过对比图6和图7可还可以看出，整体道床和浮置板道床混凝土垫层在横向和纵向的动应力分布规律不同，整体道床在横向的动应力分布有峰值出现，浮置板道床混凝土垫层在横向动应力分布平缓；而在纵向情况下，整体道床的动应力分布相比于浮置板道床混凝土垫层要平缓得多。

2.2隧道衬砌部分计算结果分析2.2.1 动应力云图分析

图9、10给出了2种不同道床情况下隧道衬砌应力的分布云图，通过对比图9、10可知，2种不同道床情况下隧道衬砌动应力的分布规律类似，最大动应力均出现在隧道衬砌最低点与土体接触位置，整体道床隧道衬砌动应力最大值为152 kPa，浮置板道床隧道衬砌动应力最大值为106 kPa，不同点在于整体道床隧道衬砌动应力扩散范围更大。

2.2.2衬砌考察点应力分布规律

图11～13给出了2种道床下，考察点1、2、3沿纵向动应力分布比较曲线。

图6　考察点4沿横向动应力分布　

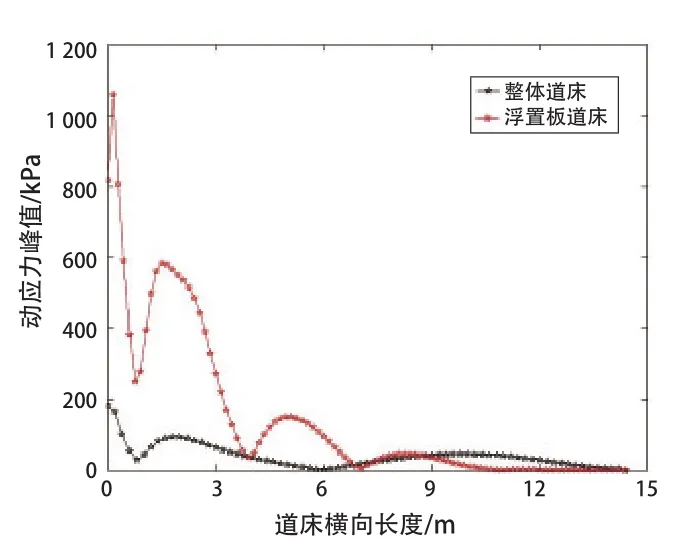
图7　考察点4沿纵向动应力分布

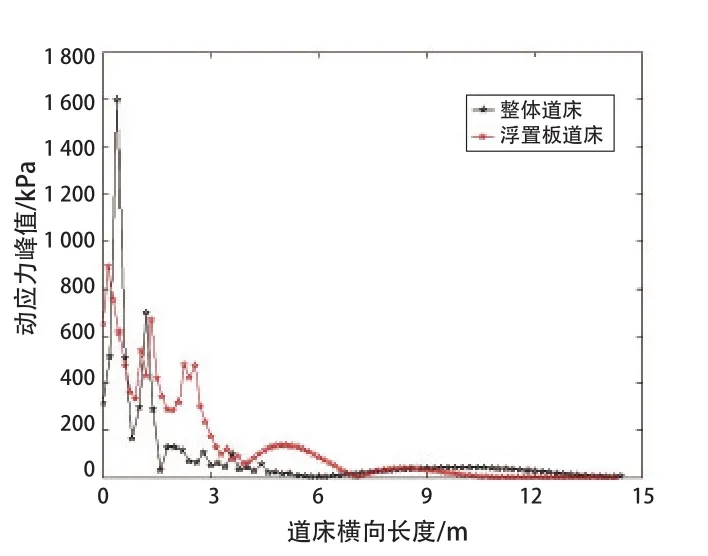
图8　考察点5沿纵向动应力分布

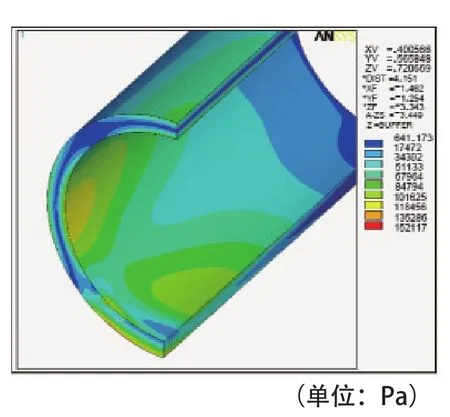
图9　整体道床衬砌动应力云图

图10　浮置板道床衬砌动应力云图

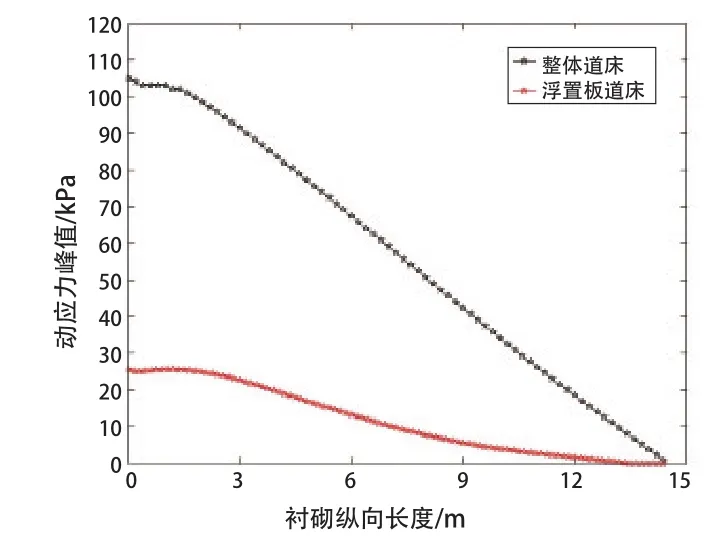
图11　考察点1沿纵向动应力分布

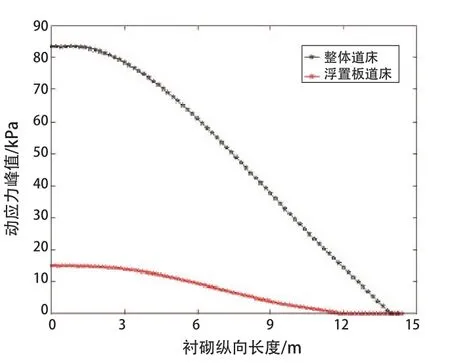
图12　考察点2沿纵向动应力分布

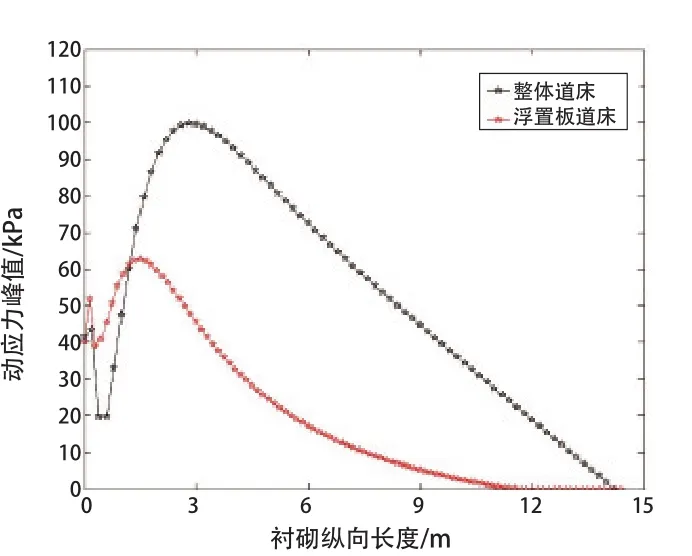
图13　考察点3沿纵向应力分布比较

(1）由图11、12可知，考察点1和考察点2的纵向动应力分布规律与道床类型无明显的关联性。对于整体道床的情况，动应力在加载点附近1 m范围内动应力峰值基本不变，大小为84 kPa，在1 m范围以外呈现线性衰减；同样，对于浮置板道床情况，动应力在加载点附近3 m范围内动应力峰值基本不变，大小为18 kPa，在3 m范围以外呈现线性衰减规律。

(2）由图13可知，在2种道床类型下，考察点3位置沿纵向的动应力分布（忽略加荷位置0.6 m范围内应力变化）均呈现抛物线似的变化规律。整体道床在0.6～3 m范围内线性增加，在3～15 m范围内线性衰减，最大动应力值为100 kPa；浮置板道床在0.6～1.5 m范围内线性增加，在1.5～12 m范围内曲线式衰减，最大动应力值为63 kPa。

图14、15给出了2种道床下，衬砌内、外壁环向动应力分布曲线。

(1）由图14可见，2种道床类型下衬砌内壁环向从-90°到90°的动应力分布形状类似，均呈现出波浪式的分布规律。整体道床情况下，动应力3次峰值分别出现在-55°、-10°和90°位置，对应的动应力峰值分别为120、110、85 kPa；浮置板道床情况下，动应力3次峰值分别出现在-70°、-40°和90°位置，对应的动应力峰值分别为52、50、15 kPa。

(2）由图15可见，2种道床类型下衬砌外壁环向从-90°到90°的动应力分布形状类似，均呈现出波浪式的分布规律。整体道床情况下，动应力3次峰值分别出现在-55°、0°和90°位置，对应的动应力峰值分别为140、80、70 kPa；浮置板道床情况下，动应力3次峰值分别出现在-70°、-30°和90°位置，对应的动应力峰值分别为90、30、16 kPa。

2.3土体部分计算结果分析2.3.1 动应力云图分析

图16、17给出了2种道床下土体动应力云图，通过对比图16、17可以看出，轮轨动荷载对土体的影响范围沿纵向长度均很短，最大土体动应力均出现在土体与隧道衬砌侧壁接触位置，其大小分别为1.1 kPa（整体道床）、0.55 kPa（浮置板道床）。

2.3.2土体考察点应力分布规律

由于土体沉降位移的评价标准是土体剪切强度大小，所以考察应力强度SINT应力可以更好地反映2种道床类型对于土体长期附加沉降的影响。由图18可以看出，SINT应力分布趋势与道床类型无关，2种道床类型下在-90°到0°的范围内动应力基本保持不变，在0°到90°的范围内呈现线性衰减。而整体道床下土体动应力最大值为0.9 kPa，浮置板道床下土体动应力最大值为0.46 kPa。

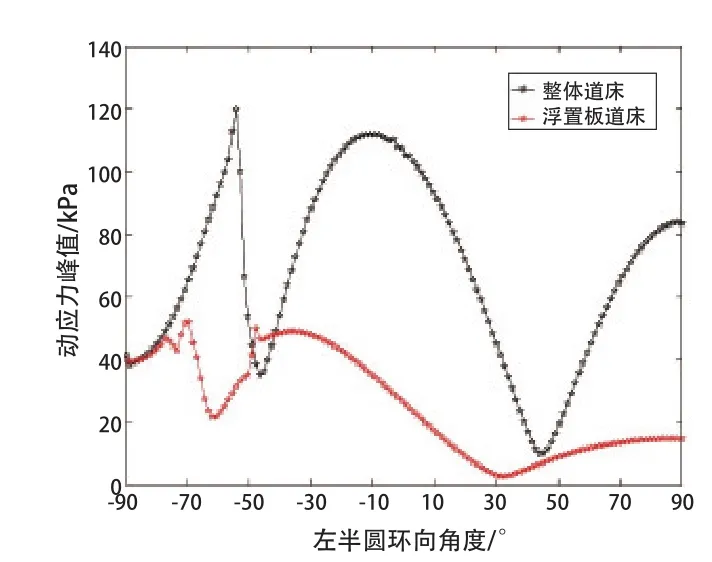
图14　衬砌内壁环向动应力分布

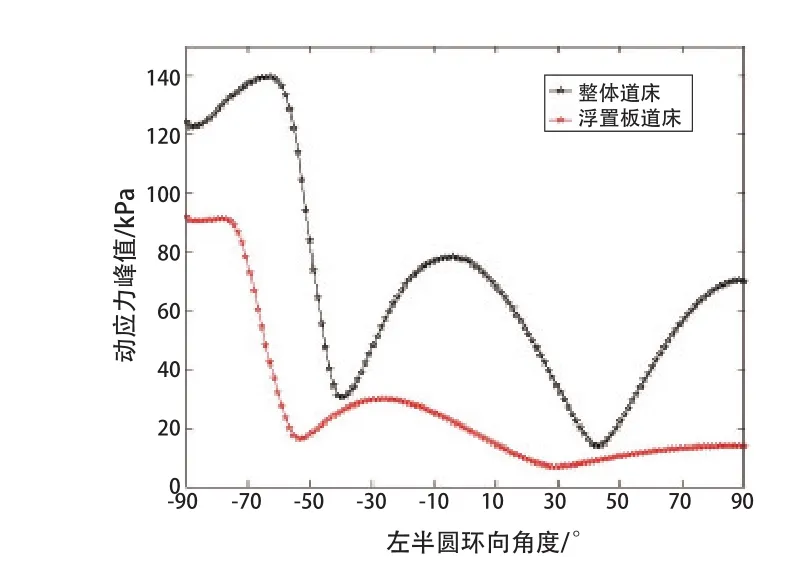
图15　衬砌外壁环向动应力分布

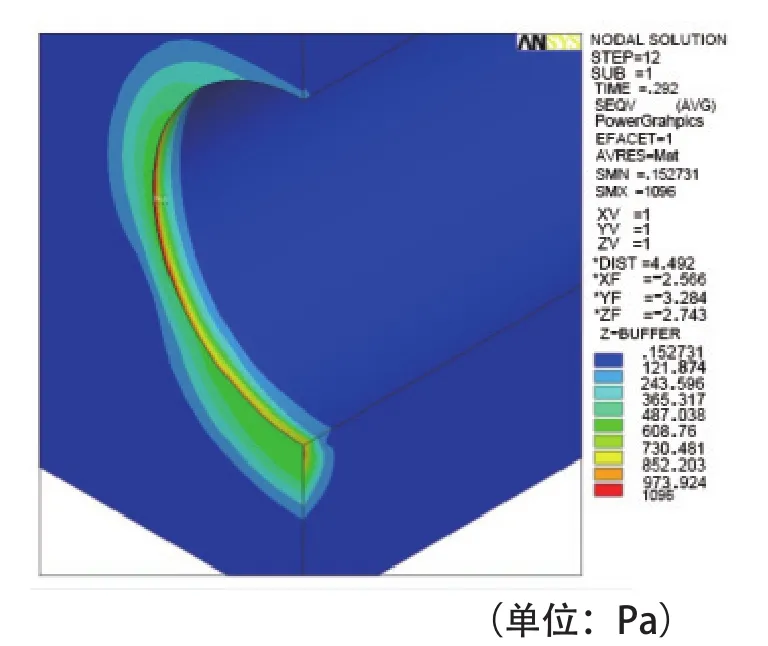
图16　整体道床下土体动应力云图

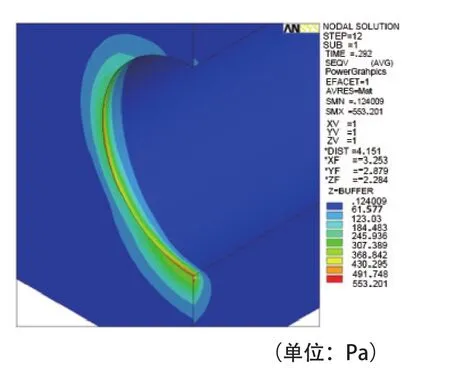
图17　浮置板道床下土体动应力云图

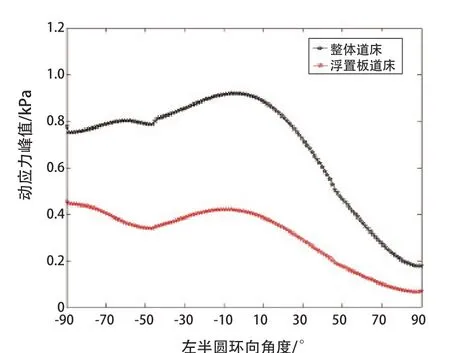
图18　土体环向SINT应力分布

3　结论

(1）整体道床对应的衬砌侧面、顶面的动应力纵向分布呈现出线性衰减，与浮置板道床相对应的动应力相对很小且衰减很缓慢。

(2）整体道床和浮置板道床在衬砌底面的动应力纵向分布均近似呈现出倒“V”字形，且整体道床动应力更大。

(3）衬砌内壁的环向动应力分布规律和大小与道床类型关系巨大，整体道床情况下动应力沿环向有明显的峰值和峰谷的交替现象，而浮置板道床峰值和峰谷之间差异并不显著；衬砌外壁的环向动应力仅大小上与道床类型有关系，其中整体道床对动应最大应力为140 kPa，而浮置板道床最大动应力为90 kPa。

(4）整体道床和浮置板下混凝土垫层在横向和纵向的动应力分布规律不同，整体道床在横向的动应力分布有峰值出现，浮置板道床混凝土垫层在横向动应力分布平缓；而在纵向情况下，整体道床的动应力分布相比于浮置板道床混凝土垫层动应力要平缓得多。

参考文献

[1] 张震. 盾构隧道结构长期沉降研究综述[J]. 城市轨道交通研究, 2013(3).

[2] 孙晓静, 刘维宁, 张宝才. 浮置板轨道结构在城市轨道交通减振降噪上的应用[J]. 中国安全科学学报, 2005, 15(8).

[3] 刘雪珠, 陈国兴. 轨道交通荷载下路基土的动力学行为研究进展[J]. 防灾减灾工程学报, 2008, 5(2).

[4] 吴宪迎. 地铁下穿重建建筑物振动影响分析及减振对策研究[D].上海: 同济大学, 2012.

[5] 谷音, 刘晶波, 杜义欣 .三维一致粘弹性人工边界及等效粘弹性边界单元[J]. 工程力学, 2007, 12(12).

责任编辑 朱开明

Calculation and Analysis on Dynamics Stress of Tunnel Structure with Integral and Floating Slab Track

Yang Ning, Geng Chuanzhi

Abstract:By using the finite element software ANSYS, the paper establishes the 3D model under the tunnel structure conditions of slab track with monolithic and fl oating slab. By inputing the corresponding measured wheel-rail force, the paper calculates the tunnel substructure dynamic stress distribution and quantity under the 2 different track beds. The paper makes conclusion that the tunnel substructure dynamic stress effect for the fl oating slab track compared to the monolithic track bed is much smaller, and both horizontal and longitudinal dynamic stress distribution is more uniform and reasonable. From a long-term point of view and in the premise of having satisfi ed the vibration and noise reduction functions, the steel spring floating slab track structure can effectively reduce wheel-rail force, therefore reducing the additional settlement of the tunnel structures.

Keywords:metro tunnel, monolithic track bed, floating slab track structure, dynamic stress, calculation and analysis

收稿日期2014-06-23