改进的强跟踪容积卡尔曼滤波的机动目标跟踪*1



改进的强跟踪容积卡尔曼滤波的机动目标跟踪*1

张恒，高敏,徐超

(军械工程学院 导弹工程系，河北 石家庄050003)

摘要：机动目标的跟踪在实际中有着广泛的应用，其核心问题是机动建模和滤波算法。采用当前统计模型和容积卡尔曼滤波对机动目标进行跟踪。针对容积卡尔曼滤波在目标突发机动时跟踪性能较差的问题，借鉴强跟踪滤波思想，将渐消因子引入滤波过程，提出了一种改进的强跟踪容积卡尔曼滤波算法，该算法实现简单，估计精度高，鲁棒性强。仿真结果表明，该算法有效增强了系统对目标突发机动的自适应跟踪能力，并保持了对弱机动和非机动目标良好的跟踪性能，且运算速度较快。

关键词：机动目标；当前统计模型；容积卡尔曼滤波；强跟踪滤波器

0引言

在实际工程中会面临各种非线性问题，非线性系统的研究变得越来越重要。作为非线性系统理论的重要研究方向，非线性滤波算法在目标跟踪领域应用广泛。而目标跟踪在精确制导、智能导航等领域大有用途，因此，深入研究非线性滤波算法，对目标跟踪问题具有重要的现实意义。

机动目标跟踪一直是目标跟踪的一个研究重点，主要包括机动建模和滤波算法两部分[1]，其主要思想是将目标机动等价为系统状态噪声的加入，并依据过程噪声统计特性建立相应的目标运动模型，然后利用非线性滤波算法进行状态估计[1-2]。根据对状态噪声统计特性的不同假设，提出了不同的机动模型，其中应用较为广泛的有 Singer 模型、当前统计模型(current statistical model，CS)、Jerk模型、交互式多模型(interacting multiple model，IMM)以及基于机动检测的跟踪算法等。基于机动检测的跟踪算法存在暂态误差和时间滞后等问题[3]；交互式多模型依赖于各个模型的性能以及模型集的选择，而且对于弱机动和非机动目标采用IMM算法会造成资源的浪费[4]；Jerk模型引入加加速度，可得到对目标加速度更精确的估计，有较高的跟踪精度，但是在阶跃机动的跟踪中存在稳态确定性误差[1,5]，影响了其应用；CS模型是对Singer模型的发展，更关心目标机动的当前统计特性，能自适应地调整过程噪声，能够很好地实现目标自适应跟踪[6]，性能优于Singer模型。

非线性滤波问题来源于含噪声观测值非线性随机系统的状态估计问题[7]。扩展卡尔曼滤波(extended Kalman filter，EKF)是将非线性函数进行泰勒级数展开，取其一阶项或二阶项，从而将非线性问题线性化，计算简单，因而获得了广泛的应用。而对于强非线性系统，EKF误差较大，滤波精度降低，甚至引起滤波发散，而且EKF必须解算雅可比矩阵，增加了解决问题的难度。为了克服上述缺陷，Juiler等人[8]提出了无迹卡尔曼滤波算法(unscented Kalman filter，UKF),该算法采用一组确定权值的采样点来逼近非线性分布来解决非线性问题，不需要对非线性系统进行线性化，性能优于EKF，但是UKF需要对参数进行合理选择才能取得较好的滤波效果。近年来，Arasaratnam等人[9]提出了一种新颖的非线性滤波算法，容积卡尔曼滤波算法(cubature Kalman filter，CKF)使用基于球面径向积分准则的数值积分方法计算非线性变换的随机变量后的均值和协方差，CKF算法实现简单，滤波精度高。

实际应用中，机动目标很可能出现突变机动，但是CKF算法在当系统处于平稳状态时，对突变状态的自适应估计能力较差。这是由于增益矩阵对预测残差突变反应滞后造成的[10]。本文将强跟踪滤波算法[11-12]的思想引入到CKF中，利用渐消因子实时调整增益矩阵，从而增强了系统对突变状态的自适应跟踪能力。本文利用CS模型对机动目标进行建模，然后通过提出的改进的强跟踪容积卡尔曼滤波算法(improved strong tracking cubature Kalman filter，ISTCKF)对机动目标的状态进行估计，从而达到对机动目标的自适应跟踪。

1目标跟踪运动模型

当前统计模型是周宏仁[6]于1983年提出来的。该算法采用修正瑞利分布来描述机动加速度的统计特性，具有自适应零均值的特点，是对Singer模型的发展改进。该模型在对目标状态进行估计的同时，利用“当前”加速度均值实时地修正加速度分布，并通过方差调整下一时刻的滤波增益，实现了闭环自适应跟踪。

设目标运动状态方程为

(1)

式中：F(k)为状态转移矩阵；G(k)为输入控制矩阵，即

(2)

(3)

W(k)为高斯白噪声，且其协方差为

(4)

(5)

amax，a-max分别为目标正、负最大加速度。

2容积卡尔曼滤波与强跟踪

2.1容积卡尔曼滤波算法

容积卡尔曼滤波(cubature Kalman filter，CKF)算法由高斯域贝叶斯滤波理论推导而来，该理论将非线性滤波转化为非线性函数和高斯概率密度之乘积的积分求解问题[7]。对于如下积分

I(f)=∫Rnf(x)exp(-xTx)dx，

(6)

式中：Rn为积分域；x为状态向量；f(x)为非线性函数。

CKF算法利用三阶球面-径向容积积分准则，采用2n个等权值的容积点ξi来实现非线性近似，即

(7)

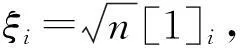
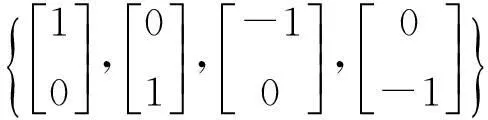
CKF算法流程描述如下：

(1) 时间更新

1) 计算容积点

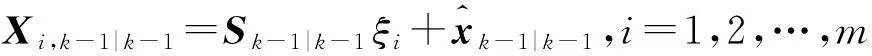
(8)

2) 容积点传播

(9)

3) 状态预测估计和预测误差协方差

(10)

(11)

(2) 量测更新

1) 计算容积点

(12)

2) 容积点传播

Zi,k|k-1=h(Xi,k|k-1,uk).

(13)

3) 量测预测值估计，新息协方差矩阵和交叉协方差矩阵

(14)

(15)

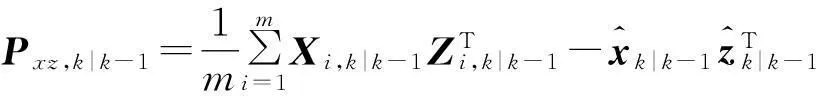
(16)

4) 卡尔曼增益、状态更新方差和协方差更新方程

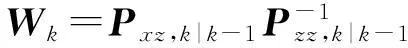
(17)

(18)

(19)

2.2强跟踪

滤波过程中状态突变时，过去数据对当前滤波值影响较大，因此往往不能很好地反应当前状态估计，很难实现自适应跟踪。强跟踪滤波算法建立在输出残差正交性原理之上，其通过引入渐消因子，将包含在残差序列里的有效信息提取出来，实时调整增益矩阵，具有自适应跟踪状态变化的能力。强跟踪滤波器将渐消因子引入到一步预测协方差矩阵中，以削减过去数据对当前滤波值得影响，其渐消因子λk+1计算方法为

(20)

式中：

(21)

tr(·)表示求矩阵的迹。

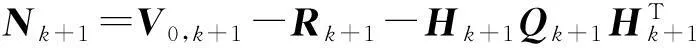
(22)

(23)

式中：V0,k+1为残差协方差矩阵，且

(24)

3强跟踪容积卡尔曼滤波

CKF算法虽然实现简单、估计精度高，但是该算法在系统达到平稳状态时，对目标突变机动的自适应跟踪能力较差。这是由于系统状态平稳时，CKF算法的增益矩阵将趋于极小值，当状态发生突变时，预测残差也发生较大变化，但此时系统增益矩阵仍保持为极小值，并不会随残差的变化而实时地自适应调整，使增益矩阵达不到最优。利用强跟踪的思想，将渐消因子引入到CKF算法的一步预测协方差矩阵，以削减过去数据对当前滤波值的影响，从而自适应调整增益矩阵，达到稳定跟踪的目的。

计算渐消因子需要计算雅可比矩阵Φ和Hk+1，但二者无法直接从CKF算法得到，需要加以改进，文献[13]给出了改进的渐消因子的求法，如下

(25)

(26)

然而，强跟踪滤波对状态估计过于依赖量测值，虽然理论上可以得到最优估计，但是由于残差协方差矩阵V0,k+1对真实的残差方差近似不够准确，导致对判定滤波异常的阈值设置较小，使得滤波增益达不到最优，且其估计值也不够平滑[14]。

文献[14]对改进的强跟踪算法渐消因子引入弱化因子β，将判定滤波异常的阈值提高到βC0,k+1(C0,k+1为滤波残差)，可大大降低正常工作情况下误判滤波发散的概率，同时提高了滤波器的精度。如下：

(27)

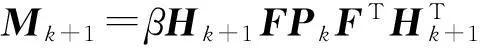
(28)

(29)

结合公式(20)，(21)，(24)即可求得改进的渐消因子λk+1，从而将ISTCKF算法中公式(11)预测误差协方差Pk+1|k更新为式(30)即可得到改进的强跟踪容积卡尔曼滤波算法滤波过程。

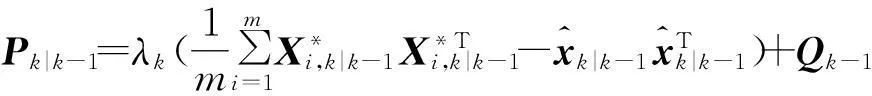
(30)

4仿真实验及分析

4.1仿真场景

为了验证本文机动目标跟踪算法的有效性，本文对阶跃机动和圆机动以及非机动进行了仿真验证，并与CKF和UKF算法进行了比较。仿真是在直角坐标系二维平面内进行的，x轴和y轴上的量测噪声均是均值为0、标准偏差为50 m的高斯序列，扫描周期为0.25 s，机动频率为0.05。在当前统计模型算法中，最大机动加速度设为amax=120 m/s2，仿真次数为100次。目标运动轨迹设定为：目标初始在x轴做匀速运动，初速200 m/s，随后以加速度100 m/s2减速为0；在第68～84个扫描区间，以加速度200 m/s2沿y轴先加速至400 m/s再减速为零；第84～124个扫描区间沿x轴以加速度100 m/s2加速至300 m/s，随后保持匀速运动；第124～170个扫描区间，以向心加速度80 m/s2做180°匀速圆机动；第170～210个扫描区间，沿x轴保持匀速运动；第210～226个扫描区间，在x轴上以加速度100 m/s2先减速再加速，y轴上以加速度100 m/s2先加速再减速；随后沿x轴以速度300 m/s保持匀速运动。运动轨迹如图1所示。

图1　目标运动轨迹Fig.1　Curve of target tracks

4.2仿真结果及分析

为克服初始状态对滤波精度的影响，这里统一假定滤波初始状态为

(-5 750,100,0,-800,0,0)T，

为了公平比较各非线性滤波算法，进行100次独立仿真取其平均。将本文改进的强跟踪容积卡尔曼滤波算法(ISTCKF)与CKF,UKF进行比较。图2表示3种滤波算法的跟踪轨迹对比。

图2　3种滤波算法的跟踪轨迹对比Fig.2　Comparison of tracking curves on　　　three filtering algorithms

由图2可见，本文提出的ISTCKF跟踪比CKF和UKF更稳定，跟踪误差更小，在目标非机动和弱机动时，ISTCKF保持了较好的跟踪性能，与CKF相当，优于UKF，尤其是在状态突变的时刻，跟踪稳定，收敛速度更快。同时CKF跟踪性能略优于UKF。为定量比较各非线性滤波算法性能，定义均方根误差(RMSE)为

(31)

图3和表1表明本文的ISTCKF算法在各坐标方向的滤波误差明显小于其他非线性滤波器，尤其表现在目标状态突变处。CKF的均方误差性能要好于UKF。同时，也发现ISTCKF对运动目标，尤其是阶跃机动目标位置和速度具有最强的跟踪能力，能自适应地跟踪状态较大变化，CKF的跟踪能力与UKF相差不大，CKF略优于UKF。

图3　各方向轴状态估计均方误差(RMSE)Fig.3　Curves of state estimation RMSE along x-axis and y-axis

算法RMSE均值/mxx·yy·UKF3.96896.33863.81756.8328CKF2.90545.27113.11045.7971ISTCKF2.70484.95682.62275.2166

表2列出了各滤波算法的运算时间。从表中可知，ISTCKF的运算时间相比CKF略有增加，但对滤波器整体滤波性能影响较小，UKF在3种算法中运算时间最短。

表2　各算法运行时间

5结束语

本文主要针对传统容积卡尔曼滤波在目标发生突变机动时跟踪性能下降的问题，借鉴了强跟踪滤波器的思想，结合当前统计模型，提出了一种改进的强跟踪容积卡尔曼滤波算法，增强了系统对强机动的自适应跟踪能力。仿真结果表明，跟踪非机动和弱机动目标时，ISTCKF性能和CKF相当，同时优于UKF，而跟踪突发机动目标时，ISTCKF性能明显优于CKF和UKF，实现了自适应跟踪。

参考文献：

[1]刘望生,李亚安,崔琳. 高度机动目标Jerk模型及改进算法[J].兵工学报,2012,33(4):385-389.

LIU Wang-sheng, LI Ya-an, CUI Lin. An Improved Algorithm for High Maneuvering Target Based on Jerk Model[J]. Acta Armamentarii, 2012,33(4):385-389.

[2]李明月,时光煜,温永强. 改进的高机动Jerk模型跟踪算法[J].电光与控制,2013,20(5):40-43.

LI Ming-yue, SHI Guang-yu, WEN Yong-qiang. An Improved Jerk Model and Algorithm for Tracking Highly Maneuvering Targets[J]. Electronics Optics & Control, 2013,20(5):40-43.

[3]刘望生,李亚安,崔琳. 基于当前统计模型的机动目标自适应强跟踪算法[J].系统工程与电子技术,2011,33(9):1937-1940.

LIU Wang-sheng, LI Ya-an, CUI Lin. Adaptive Strong Tracking Algorithm for Maneuvering Targets Based on Current Statistical Model[J]. Systems Engineering and Electronics, 2011,33(9):1937-1940.

[4]何友,修建娟,张晶炜，等.雷达数据处理及应用 [M].2版.北京:电子工业出版社,2009.

HE You, XIU Jian-juan, ZHANG Jing-wei，et al. Radar Data Processing With Applications [M].2nd ed. Beijing: Publishing House of Electronics Industry, 2009.

[5]乔向东,王宝树. 高度机动目标的“当前”统计Jerk模型[J].系统工程与电子技术,2002,24(6):53-56.

QIAO Xiang-dong, WANG Bao-shu. A CS-Jerk Model for Tracking Highly Maneuvering Targets[J]. Systems Engineering and Electronics, 2002,24(6):53-56.

[6]周宏仁,敬忠良,王培德.机动目标跟踪[M].北京：国防工业出版社,1991.

ZHOU Hong-ren, JING Zhong-liang, WANG Pei-de. Maneuvering Targets Tracking[M].Beijing:National Defence Industry Press,1991.

[7]张鑫春,郭承军.均方根嵌入式容积卡尔曼滤波[J].控制理论与应用,2013,30(9):1116-1121.

ZHANG Xin-chun, GUO Cheng-jun. Square-Root Imbedded Cubature Kalman Filtering[J]. Control Theory & Applications, 2013,30(9):1116-1121.

[8]JULIER S J, UHLMANN J K. A New Method for the Nonlinear Transformation of Means and Covariances in Filters and Estimators[J].IEEE Trans. on AC,45(3),2000:477-482.

[9]ARASARATNAM I, HAYKIN S. Cubature Kalman Filters[J]. IEEE Trans. on Automatic Control,2009,54(6):1254-1269.

[10]霍光,李冬海,李晶.基于强跟踪容积卡尔曼滤波的单站无源跟踪算法[J].现代雷达,2013,35(11): 52-57.

HUO Guang, LI Dong-hai, LI Jing. A Single Observer Passive Tracking Algorithm Based on Strong Tracking Cubature Kalman Filter[J]. Modern Radar,2013, 35(11): 52-57.

[11]周东华,席裕庚,张钟俊.非线性系统带次优渐消因子的扩展卡尔曼滤波[J].控制与决策,1990,5(5):1-6.

ZHOU Dong-hua, XI Yu-geng, ZHANG Zhong-jun. The Extended Kalman Filter with Suboptimal Fading Factor in Nonlinear System[J]. Control and Decision, 1990,5(5):1-6.

[12]周东华,席裕庚,张钟俊.一种带多重次优渐消因子的扩展卡尔曼滤波[J].自动化学报,1991,17(6):689-695.

ZHOU Dong-hua, XI Yu-geng, ZHANG Zhong-jun. An Extended Kalman Filter with Multiple Suboptimal Fading Factor[J]. Acta Automatica Sinica, 1991,17(6):689-695.

[13]王小旭,赵琳,夏全喜,等. 基于Unscented变换的强跟踪滤波器[J].控制与决策,2010,25(7):1063-1068.

WANG Xiao-xu, ZHAO Lin, XIA Quan-xi,et al. Strong Tracking Filter Based on Unscented Transformation[J]. Control and Decision, 2010,25(7):1063-1068.

[14]葛磊.容积卡尔曼滤波算法研究及其在导航中的应用[D].哈尔滨：哈尔滨工程大学,2013.

GE Lei. Research on Cubature Kalman Filter and Its Application for Navigation[D]. Harbin： Harbin Engineering University,2013.

Maneuvering Target Tracking Algorithm Based on Improved Strong Tracking Cubature Kalman Filters

ZHANG Heng，GAO Min，XU Chao

(Ordnance Engineering College,Missile Engineering Department,Hebei Shijiazhuang 050003, China)

Abstract:Tracking of maneuvering targets is widely used in practice, and its core issues are system model and filtering algorithm. The current statistical model and cubature Kalman filter are applied to maneuvering target tracking. For the degradation of adaptive tracking performance in sudden maneuvering of targets, an improved strong tracking cubature Kalman filter algorithm is proposed by introducing the fading factor into filtering process learnt from strong tracking filter. The algorithm has a simple implementation, high estimation accuracy and good robustness. The simulation results show that the adaptive tracking performance for the sudden maneuvering of targets is improved effectively and a good tracking performance for weak motion and the nonmaneuverable is maintained by the proposed algorithm, and the arithmetic speed is considerable.

Key words:maneuvering target; current statistical model; cubature Kalman filter; strong tracking filter

中图分类号：TN953；TP301.6

文献标志码：A

文章编号：1009-086X(2015)-06-0142-06

doi:10.3969/j.issn.1009-086x.2015.06.024

通信地址：050003河北省石家庄市新华区和平西路97号军械工程学院四系E-mail：tszhangheng@163.com

作者简介：张恒(1990-)，男，河南商丘人。硕士生，主要研究方向为弹药的智能化与信息化技术。

*收稿日期：2014-08-28；修回日期：2014-10-10