基于熵权的多站纯方位目标定位分析*1



基于熵权的多站纯方位目标定位分析*1

王馨，王明宇，刘进忙

(空军工程大学 防空反导学院，陕西 西安710051)

摘要：为克服传统权值主观性强、复合性差等现象，提出了一种基于改进熵权的多站纯方位目标定位算法。算法系统分析了匀速直线运动下的目标纯方位信息，给出了目标航迹参数与位置坐标模型，并运用均方误差进行了精度分析。仿真实验表明，本算法能有效地降低估计误差，提高多站融合精度。

关键词：纯方位；熵权；目标定位；匀速直线运动；航迹参数；融合精度

0引言

多站纯方位目标运动分析是指由多个观测站从目标源获得目标一系列的方位测量值来估计目标的运动速度和位置[1-2]。在实际监测环境下，一般可测的目标数据比较有限，利用目标方位参数估计目标的运动数据进而实现其电子干扰和软硬杀伤在现代战争中有着十分重要的军事意义[3]。

近年来，纯方位目标定位分析已从不同角度进行了有效探索，并取得了一定的成果。文献[4]利用余切关系定理解决了纯方位观测的非线性问题；文献[5-7]分别讨论了纯方位目标运动分析中的最小二乘估计、加权卡尔曼滤波及其改进算法。但需要说明的是，在多个精度不同的观测站进行探测时，通常采用主观权重法对其加权系数进行解算，算法缺乏对实际统计数据的客观分析，因而存在很大的主观不确定性。针对这一问题，本文提出一种基于熵权系数的估计方法，算法的核心是根据各站的测量数据误差，利用改进熵权算法计算出各参数的熵权，从而得出更为准确、客观的估计结果。

1多站纯方位目标定位

1.1多站纯方位目标定位的基本算法

(1) 目标纯方位航迹参数估计

(1)

根据A，B的位置事先计算αAB，α0为各站目标航迹参数，由式(1)可得

(2)

(2) 确定目标位置坐标

设目标做匀速直线运动，N个纯方位观测站分别为A，B，C，…，N，其各站站址为(xA，yA)，(xB，yB)，(xC，yC)，…，(xN，yN)，各站的正北轴已校正，在某时刻ti各站同时观测(同步)或计算(异步)的方位角为β1i，β2i，β3i，…，βni，目标的直角坐标为(xi，yi)。

经过推导可得

(3)

异步情况下，计算A站的方位角函数为

实际计算过程中，各站测量精度不同，其误差一般服从正态分布，设加权系数分别为ω1，ω2，ω3，ω4，…，ωn，用加权广义逆求解得[9]

(4)

以定位后目标与传感器距离的均方误差来度量定位的精确程度[10]：

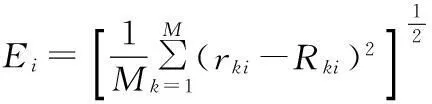
(5)

式中：Ei为是指参数估计值与真实值之差平方的期望值，值越小，精确度越高；Rki为ti时刻第k次仿真时目标距传感器距离的真实值；rki为ti时刻第k次仿真时目标距传感器距离的估计值。

根据上述计算可知，在进行多站纯方位目标定位时，权重表明了各站测量精度在目标定位中的重要程度，反映了误差精度对目标定位的影响。主观权重一般是由专家根据应用经验主观赋值，不能反映测量精度的变化情况，计算结果误差较大。为克服权重主观性强的弱点，本文以观测站的测量精度为基础，用熵权法计算各站权值，进而减小测量误差。

1.2基于熵权的多站纯方位目标定位

信息熵是对系统不确定性的描述，而熵权是体现测量误差相对激烈程度的系数，是对误差重要性的客观度量。

(1) 误差指标量化

在进行熵权计算时，为便于统一分析，常采用极值变换法将误差的实际值转化为度量值，以尽可能的消除原始指标量纲对熵权值的影响。误差一般是其值越大，效果越差，因此该指标是负向指标，即随着指标数值的增大能力减弱。其计算式为

(6)

式中：ai(j)为第ti时刻第j(0

(2) 确定信息熵

根据熵的定义，第j个传感器的误差熵为[11]

(7)

式中：

(8)

其中，γ为对bi(j)的修正，取值趋近于10-4，反映了误差经过标准化处理后的精确位数，既能保证lnpi(j)具有数学意义，又使bi(j)对熵值H(j)的影响被控制在合理范围之内。

(3) 确定差异性系数

在实际评估中，对于第j个传感器，bi(j)的差距越大，该误差值在综合评价中所起的作用越大；如果bi(j)全部相等，则该误差值在综合评价中几乎不起作用。为此，可定义差异性系数[12]：

η(j)=1-H(j)，

(9)

则当bi(j)的差距越大时，H(j)越小，η(j)越大，误差值越重要。

(4) 求解熵权

以差异性系数定义熵权公式为

(10)

分析上述算法发现，当所用误差熵值存在微小差别时，会使指标对应的熵权发生成倍数的变化，这显然与实际情况不符[13]。为避免出现熵权跳跃现象，可定义改进的熵权计算公式为[14]

(11)

式中：ξ为常数，取值趋近于传感器数量。

(5) 根据式(4)～(5)确定坐标评估位置及其误差。

2仿真算例

假设观测站n=3，传感器A位置固定为(0，0)m，B传感器的位置固定为(800，800)m，C传感器的位置固定为(1 600，1 600)m，目标初始位置为(1 000，1 200)m，并以速度(40，60)m/s做匀速直线运动[15]。方位角测量误差服从正态分布，标准差分别为σ1=3 mrad，σ2=2 mrad，σ3=1 mrad。根据正态分布规律和不同时刻的测量误差，由式(6)～(11)计算相应的熵权值。取仿真次数为M=100，结合式(1)～(5)对于主观权值和熵权值分别做100次仿真实验，并分别确定不同权值下的均方误差以衡量估计精度，结果如图1，2所示。其中，表1分别给出了主观权重和计算的熵权值，γ=10-4，ξ=4。

表1　各传感器主观权重和熵权

图1　目标与传感器的估计距离与均方误差(主观)Fig.1　Estimated distance and MSE of targets to　　　sensors for subjective weights

图2　目标与传感器的估计距离与均方误差(熵权)Fig.2　Estimated distance and MSE of targets to　　　sensors for entropy weights

分析图1，2可得以下结论：

(1) 熵权算法是对测量误差相对激烈程度的反映，综合说明了误差的变化特性和稳定特性，且具有自适应性质。如表1所示，熵权值满足：传感器3>传感器2>传感器1，其大小及排序与误差大小相一致，因而更能提高准确度。

(2) 熵权算法所得估计值更接近于真实值。如图1，2所示，在相同的运算条件下，熵权算法所得估计距离随着仿真次数的增大变化幅度逐渐变小，目标与传感器距离的估计值更逼近于真实值，说明三站融合的结果得到的目标定位值随着权重的变化与真实位置更接近，这是由于熵权算法的自适应特性能适时调整测量误差，避免了部分时段误差较大的现象，从而使估计值更加精确，提高了三站融合精度。

(3) 熵权算法均方误差小且收敛速度快。图1，2下半部分表示目标与传感器距离的均方误差值，其趋势是随时间增大而逐步稳定，其中，熵权法所得估计距离均方误差在15 m左右，主观权重所得估计距离均方误差在20 m左右。

3结束语

本文结合纯方位条件下的目标航迹参数与位置坐标，给出了一种基于改进熵权的目标定位算法，并通过算例仿真验证了算法的正确性和可行性。该方法的特点是：

(1) 数据收集成本低、计算过程简便、模型可拓展性和稳定性较强。

(2) 实现了误差权重的优化处理，克服了权值跳跃、主观性强等缺点。

(3) 算法所得估计距离误差较小且收敛性强。

(4) 算法根据传感器位置和误差分析求出了误差权重及评估结果，便于仿真和分析。

参考文献：

[1]刘进忙. 空中目标分坐标滤波与参数航迹融合技术研究[D]. 西安：西安电子科技大学，2012.

LIU Jin-mang. Research on Independent Coordinates Filtering and Parameterized Trajectory Fusion Technology for Aerial Targets[D]. Xi′an: Xidian University, 2012.

[2]赵晓飞. 单站纯方位无源探测定位的若干技术研究[D]. 上海：上海交通大学，2007.

ZHAO Xiao-fei. Research of Some Technologies on Bearing-Only System [D]. Shanghai: Shanghai Jiaotong University, 2007.

[3]郭福成. 基于运动学原理的单站无源定位与跟踪关键技术研究[D]. 长沙：国防科学技术大学，2002.

GUO Fu-cheng. Research of SOPLAT on Particle Kinematics [D]. Changsha: National University of Defense Technology, 2002.

[4]刘进忙，姬红兵，左涛，等. 纯方位观测的航迹不变量目标跟踪算法[J]. 西安电子科技大学学报，2008，35(1)：49-53.

LIU Jin-mang, JI Hong-bing,ZUO Tao,et al. Trajectory Invariable-Information Target Tracking Algorithm with Bearing-Only Measurement[J]. Journal of Xidian University, 2008, 35(1): 49-53.

[5]刘健，刘忠. 纯方位目标运动分析的无偏最小二乘估计算法研究[J]. 武汉理工大学学报，2010，34(2)：262-265.

LIU Jian, LIU Zhong. Study on Algorithm of Unbiased Least Square Estimator for Bearings-Only Target Motion Analysis[J]. Journal of Wuhan University of Technology, 2010, 34(2): 262-265.

[6]詹艳梅，孙进才，胡友峰，等. 纯方位目标运动分析的自适应算法[J]. 西北工业大学学报，2002，20(4)：647-650.

ZHAN Yan-mei, SUN Jin-cai,HU You-feng,et al. An Effective Adaptive Algorithm for Bearings-Only Target Motion Analysis[J]. Journal of Northwestern Polytechnical University, 2002, 20(4): 647-650.

[7]曲长文，徐征,苏峰，等. 一种双站纯方位快速渐进无偏定位算法研究[J]. 现代雷达，2011，33(6)：41-45.

QU Chang-wen, XU Zheng,SU Feng,et al. A Study on Asymptotically Unbiased Location Algorithm with Bearings-Only Measurements by Two Stations[J]. Modern Radar, 2011, 33(6): 41-45.

[8]孙仲康，郭福成，冯道旺,等. 单站无源定位跟踪技术[M]．北京：国防工业出版社，2008．

SUN Zhong-kang, GUO Fu-cheng, FENG Dao-wang, et al．Passive Location and Tracking Technology by Single Observer[M]．Beijing: National Defense Industry Press, 2008.

[9]刘忠. 纯方位目标定位分析[M]．北京：国防工业出版社，2009．

LIU Zhong．TMA-Target Motion Analysis [M]．Beijing: National Defense Industry Press, 2009.

[10]张近乐，任杰. 熵理论中熵及熵权计算式的不足与修正[J]. 统计与信息论坛，2011，26(1)：3-5.

ZHANG Jin-le, REN Jie. The Deficiencies and Amendments of the Calculation Formulate of Entropy and Entropy Weight in the Theory of Entropy[J]. Statistics & Information Forum, 2011, 26(1): 3-5.

[11]GONG Shu-feng,LONG Wei-jun,HUANG Hao,et al. Polyphase Orthogonal Sequences Design for Opportunistic Array Radar via HGA[J]. Journal of Systems Engineering and Electronics, 2013,24(1): 60-67.

[12]LENKARAN A, SIMON H, ROBERT J E. Discrete-Time Nonlinear Filtering Algorithms Using Gauss-Hermite Quadrature [J].Proceedings of the IEEE，2007, 95(5): 953-977.

[13]赵晶英，陈英俊,项顺伯，等. 物流企业遴选业务项目的熵权灰色关联算法设计[J]. 浙江大学学报，2012，39(4)：484-488.

ZHAO Jing-ying, CHEN Ying-jun,XIANG Shun-bo,et al. Algorithm Design of Entropy Grey Relation for Logistics Enterprise Business Project Selection[J]. Journal of Zhejiang University (Science Edition), 2012, 39(4): 484-488.

[14]唐政，孙超,刘宗伟，等. 基于灰色层次分析法的水声对抗系统性能评估[J]. 兵工学报，2012，33(4)：432-436.

TANG Zheng, SUN Chao,LIU Zong-wei,et al. Research on Efficiency Evaluation for Underwater Acoustic Countermeasure System Based on Grey Hierarchy Analysis[J]. Acta Armamentarii, 2012, 33(4): 432-436.

[15]Merrill I Skolnik[美]. 雷达系统导论[M].左群声，徐国良，马林，等，译.北京：电子工业出版社，2010.

Merrill I Skolnik. Introduction to Radar Systems[M].ZUO Qun-sheng,XU Guo-liang,MA lin,et al,Traslated. Beijing：Publishing House of Electronics Industry，2010.

Analysis of Bearings Only Multiple Observers Location on Entropy Weight

WANG Xin, WANG Ming-yu, LIU Jin-mang

(AFEU，Air and Missile Defense College,Shaanxi Xi′an 710051, China)

Abstract:To solve the strong subjectivity and poor compound of traditional weight, a bearingsonly multiple observers target localization algorithm based on improved entropy weight is proposed. With the analysis of target bearingsonly information under uniform motion in a straight line, target tracking parameters and location coordinates are given, and the accuracy of algorithm based on the mean square error is analyzed. The simulation result shows the algorithm reduces the estimation error and improves the multiple observers fusion accuracy effectively.

Key words:bearings-only; entropy weight; target localization; uniform motion in a straight line; tracking parameters; fusion accuracy

中图分类号：TN953+.7

文献标志码：A

文章编号：1009-086X(2015)-06-0119-05

doi:10.3969/j.issn.1009-086x.2015.06.020

通信地址：710051西安市长乐东路空军工程大学防空反导学院研一队E-mail：389987728@qq.com

作者简介：王馨(1990-)，女，山东潍坊人。硕士生，主要从事组网反隐身技术研究。

*收稿日期：2014-10-13；修回日期：2015-01-10