等效滞回模型在锂离子电池SOC估计中的应用*
2015-03-09吕继考刘继光
程 泽,吕继考,刘继光,王 莉
(天津大学 电气与自动化工程学院,天津 300072)
等效滞回模型在锂离子电池SOC估计中的应用*
程 泽,吕继考†,刘继光,王 莉
(天津大学 电气与自动化工程学院,天津 300072)
锂离子电池荷电状态的快速准确估计是电池管理系统的关键技术之一.针对锂离子电池这一动态非线性系统,通过测试分析锂离子电池的滞回特性,建立了锂离子电池的二阶RC滞回模型,并利用容积卡尔曼滤波算法对电池荷电状态进行估算.实验结果表明,该模型能较好地体现电池的动态滞回特性,而且容积卡尔曼滤波算法在估算过程中能保持较高的精度.
锂离子电池;荷电状态;滞回模型;容积卡尔曼滤波
随着环保和节能问题的日益突出,锂离子电池由于高能量密度、高工作电压、无记忆效应、循环寿命长、无污染、质量轻、自放电小[1]以及在安全性和循环性方面的突出性能,使得它在储能动力电池领域占据越来越重要的地位, 准确估计锂离子电池的荷电状态(State of Charge, SOC) 也渐渐成为研究热点.
可靠的电池模型是电池SOC准确估计的前提条件,锂离子电池模型的准确度直接影响SOC估计的精度.滞回特性是锂离子电池的基本特性之一,它是指电池在充电过程的开路电压(Open Circuit Voltage, OCV)与放电过程的开路电压不一致的现象,文献[2]介绍了产生滞回现象的原因.文献[3]在等效电路模型的基础上引进了描述滞回特性的电路参数, 该方法使得模型待估参数明显增加,参数估计成本较大.文献[4-5]分别建立了Preisach模型和Jiles Atherton模型描述锂离子电池的动态特性,上述数学模型虽然很大程度提高了精度,但模型算法复杂,计算量大,不适合工程实现.
本文针对锂离子电池充放电过程中的滞回特性提出了一种简单的基于滞回特性的锂离子电池模型,并利用容积卡尔曼滤波(Cubature Kalman Filter, CKF)算法将上述模型应用到锂离子电池的SOC估计中,从而大幅度降低了SOC估计过程中的模型误差和算法误差.
1 锂离子电池滞回特性实验分析
本文选用天津力神公司生产的磷酸铁锂动力电池LP2770102AC(电池的标称电压为3.3 V,标称容量为12.5 Ah),在Digatron动力电池测试系统上设计了室温条件下的脉冲充放电实验.测试过程中还假定锂离子电池每次充放电结束静置1 h后,电池电压均已经恢复至稳定值[6].考虑到锂离子电池在SOC<10%和SOC>90%的情况下OCV随SOC变化速度较快[7],因此为了准确地描述充放电过程中OCV-SOC曲线的变化趋势,当10%
1.1 滞回主回路特性
滞回主回路特性是指锂电池在完整SOC循环周期下的OCV-SOC特性曲线[8],锂离子电池的滞回主回路特性具体测试步骤如下:
1)先将电池充满电(SOC=100%)后静置1 h;
2)对电池进行4次脉冲放电(6.25 A放电3 min,静置1 h)至电池SOC=90%;
3)对电池进行16次脉冲放电(6.25 A放电6 min,静置1 h)至电池SOC=10%;
4)对电池进行4次脉冲放电(6.25 A充电3 min,静置1 h)至电池SOC=0%;
5)对电池进行4次脉冲充电(6.25 A充电3 min,静置1 h)至电池SOC=10%;
6)对电池进行16次脉冲充电(6.25 A充电6 min,静置1 h)至电池SOC=90%;
7)对电池进行4次脉冲充电(6.25A充电3 min,静置1 h)至电池SOC=100%.
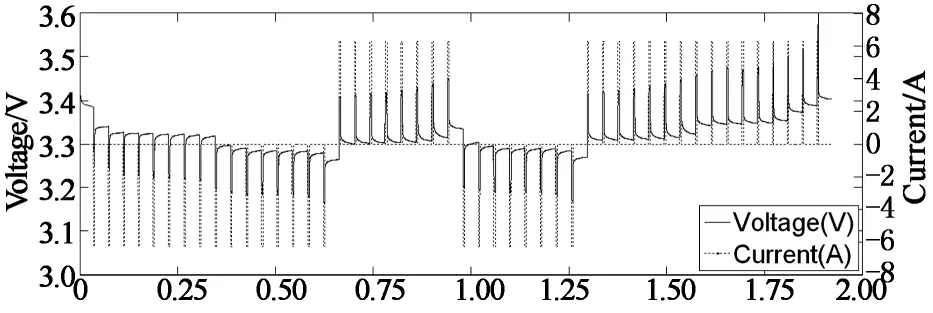
整个充放电过程时长约53 h,采样间隔为1 s.图1给出了测试过程中锂离子电池的端电压和端电流变化曲线,可以看出充放电过程中的电池端电压在SOC<10%和SOC>90%阶段变化幅度较大.

T/s
对图1中的数据分析处理后,得到锂离子电池在室温条件下静置1 h的滞回主回路特性曲线及二者差值曲线,如图2所示.

SOC(a)充放电OCV-SOC曲线

SOC(b)充放电OCV差值曲线
我们将图2(b)中的曲线分成3部分,并定义最大相对差值为:
(1)
其中Dmr表示每一部分的最大绝对差值.
当SOC<10%时,Dmr=0.16V(SOC=2.5%),Dma=15.23%;
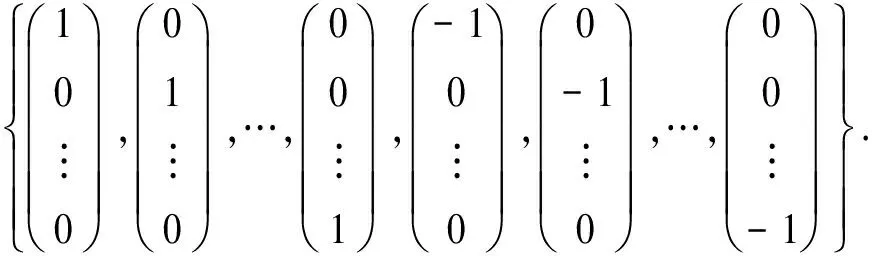
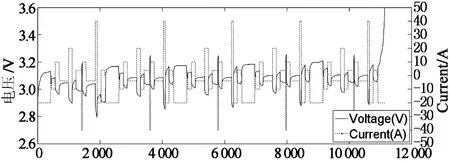
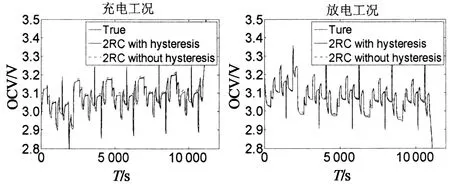
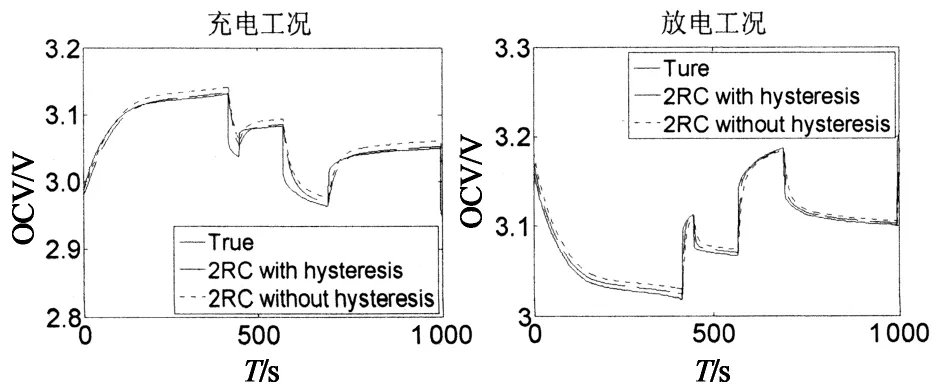
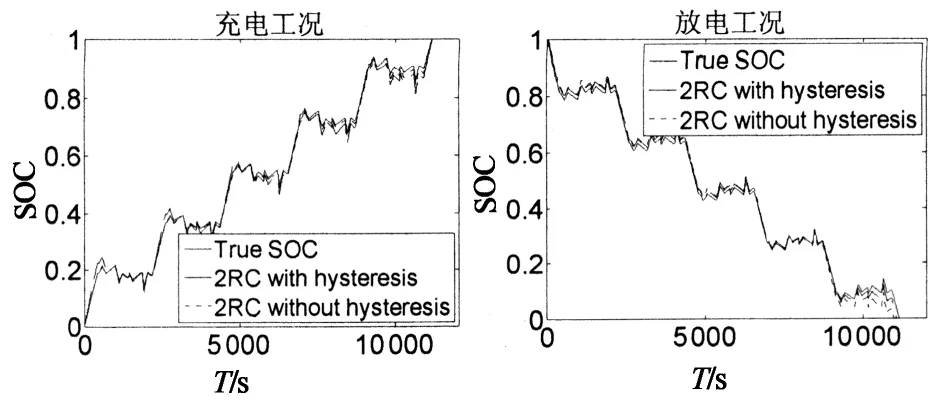
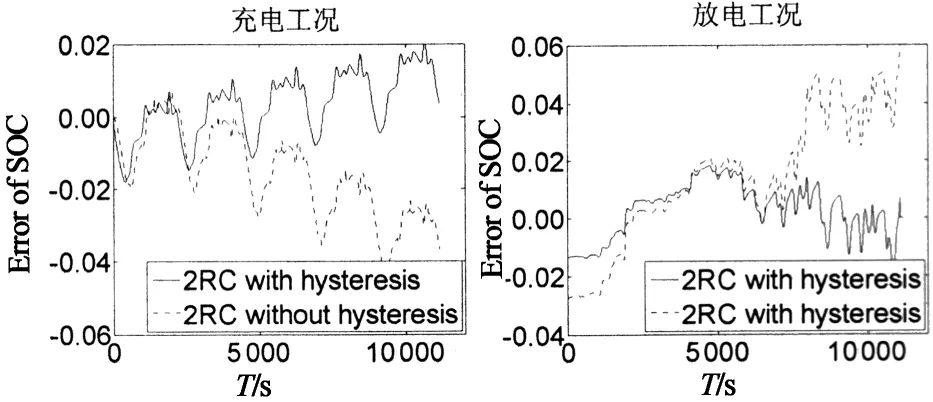
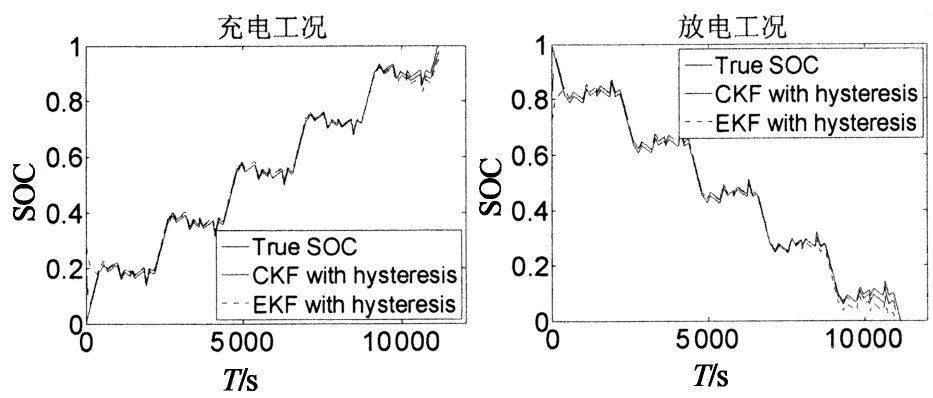
当10% 当SOC>90%时,Dmr=0.03V(SOC=97.5%),Dma=2.8%. 改变上述测试过程中的静置时间,分别将其设置为1min,5min,30min,得到不同静置时间下的OCV-SOC曲线,如图3所示.锂离子电池的滞回特性不仅是SOC的函数,而且是静置时间的函数,且随着静置时间的加长锂离子电池的滞回特性逐渐减弱,并最终趋于平滑. SOC 1.2 滞回小回路特性 与滞回主回路特性相对应,滞回小回路特性是指锂电池在局部SOC循环周期下的OCV-SOC曲线,锂离子电池的滞回小回路特性具体测试步骤如下: 1)先将电池充满电(SOC=100%)后静置1h; 2)对电池进行4次脉冲放电(6.25A放电3min,静置1h)至电池SOC=90%; 3)对电池进行12次脉冲放电(6.25A放电6min,静置1h)至电池SOC=30%; 4)对电池进行8次脉冲充电(6.25A充电6min,静置1h)至电池SOC=70%; 5)对电池进行8次脉冲放电(6.25A放电6min,静置1h)至电池SOC=30%; 6)对电池进行12次脉冲充电(6.25A充电6min,静置1h)至电池SOC=90%; 7)对电池进行4次脉冲充电(6.25A充电3min,静置1h)至电池SOC=100%. 整个充放电过程时长约53.5h,采样间隔为1s.图4给出了测试过程中锂离子电池的电压和电流变化曲线. T/s 对图4中的数据分析处理,得到锂离子电池静置1 h的滞回小回路特性曲线,如图5所示,图中箭头表示SOC的变化方向. 综合以上测试和数据,我们可以得到如下结论: 滞回特性不能被简单表述为一条或几条曲线,应该是一簇曲线. 滞回特性是电池充放电历史的函数; 滞回特性是静置时间的函数; 滞回小回路OCV-SOC曲线始终在滞回主回路OCV-SOC曲线的内部; 当电流方向改变时,OCV-SOC曲线的方向也随之改变,且随着时间的推移滞回小回路特性曲线总是逐步逼近滞回主回路特性曲线,逼近速度随二者距离的减小逐渐降低. SOC 1.3 滞回特性对SOC估计的影响 定义由滞回特性引起的SOC估计误差为: (2) 交换图2(a)中的坐标轴并做差值,得到图6所示的SOC-OCV曲线以及由滞回特性引起的SOC误差曲线. OCV/V(a)SOC-OCV曲线 OCV(b)SOC误差曲线 从图6(b)可以看出,由滞回特性引起的SOC估计误差的最大值是32.6%(OCV=3.3 V),也就是说如果我们使用充放电过程中OCV-SOC曲线的平均值估计锂离子电池的SOC会造成非常大的误差,特别是当电池的SOC在10%到90%之间时,相应的OCV-SOC曲线非常平滑,SOC相对于OCV的变化非常敏感,非常小的OCV 变化都有可能引起很大的SOC估计误差.因此在锂离子电池SOC估计过程中必须考虑滞回特性的影响. 综合考虑等效电路模型的准确度和复杂度,按照不同精度的要求,等效电路模型可分为:线性模型、静置模型、滞回模型[9-11]. 2.1 线性模型 如图7所示,线性模型将电池看作一个大电容C,电容电压为Uoc,同时串联一个小电阻R0表示电池内阻,内阻阻值随着周围环境温度和电池寿命的改变而变化. 图7 线性等效电路模型 2.2 静置模型 将电池静置特性考虑在内的电池模型称为静置模型.与线性模型比较,静置模型用可控电压源代替了大电容表示电池的电动势,用一系列的RC网络等效表示静置特性,其电压值是SOC的函数.图8给出了相应的静置模型. 2.3 滞回模型 将电池滞回特性考虑在内的电池模型称为滞回模型.本文对锂离子电池滞回特性建模的基本思想是建立一种数学模型使得锂离子电池的OCV在充电过程中逐步趋向于滞回主回路中的OCVCharge、放电过程中逐步趋向于滞回主回路中的OCVDischarge.考虑到OCV-SOC曲线越接近于滞回主回路特性曲线,其逼近速度就越小,经过多次比较筛选选取了如下模型: (3) 其中,λ为调整系数.针对本文选取的电池取λ=10. 为了验证上述模型的准确性,将测试2中得到的滞回小回路数据代入式(3),结果如图9所示,可以看出该模型输出值基本接近于锂离子电池OCV的真实值,说明上述模型可以准确地再现锂离子电池的滞回特性. 图8 静置等效电路模型 SOC 综合考虑模型精度、复杂度以及实验选用的LiFePO4,本文采用图10所示的二阶RC滞回等效电路模型. 其中Uoc(SOC)表示锂离子电池的OCV,用来描述电池的滞回特性;Ut为端电压;It为端电流;R0为欧姆内阻;Re,Ce和Rd,Cd用来描述电池的静置特性. 锂离子电池的上述参数均随着SOC的变化而变化,为了提高模型精度,本文采用递推最小二乘法估计等效电路模型的各个参数.递推最小二乘法无需存储全部数据,取得一组观测数据,便可估计一次参数,因此所需的计算量和占用的存储空间都很小,如图11所示基于脉冲放电数据的辨识结果. 图10 二阶RC滞回等效电路模型 T/s 考虑到锂离子电池模型的参数较多和高度非线性,而扩展卡尔曼滤波在状态估计过程中,存在两个缺点: 1)当非线性函数的Taylor展开式高阶项无法忽略时,线性化会使系统产生较大误差,甚至使滤波器不稳定; 2)在每个滤波周期需要计算雅克比矩阵,对于复杂系统,将大大增加滤波估计的运算量. 本文将卡尔曼滤波的另一种非线性化方法——容积卡尔曼滤波(Cubature Kalman Filter, CKF)[12]应用于锂离子电池的SOC估计中.CKF既不需要对函数进行线性化,也不需要计算 Jacobin 矩阵,算法的数值稳定性不受状态维数的影响,适用于解决从低维到高维的非线性状态估计问题,估计精度至少能精确到二阶泰勒精度. 将图10所示电池模型以SOC,Ue,Ud为状态变量,It为输入量,Ut为输出量离散化后得到的模型的状态方程和观测方程分别为: (4) Ut(k)=Uoc(SOC(k))-Ue(k)-Ud(k)- R0It(k)+vk. (5) 其中η为库仑效率,可以通过电池充放电实验得到;Qn为电池额定容量;Ts为采样周期;τe,τd是RC网络的时间常数,且τe=ReCe,τd=RdCd;It(k)为k时刻的电流,本文中,充电时It(k)>0,放电时It(k)<0;wk和vk是互不相关的高斯白噪声. 1)初始化: (6) 2)预测更新: (7) [1]i= (8) (9) (10) 3)量测更新: (11) (12) (13) (14) (15) (16) 4)状态更新: 估计卡尔曼增益,更新状态以及误差协方差阵. (17) (18) (19) 目前动力锂离子电池广泛应用于电动汽车领域,此时电池的工作特点是工作电流变化剧烈.本文选取2种DST(DynamicStressTest)工况对锂离子电池滞回模型和CKF算法进行验证,分别为充电工况和放电工况.2种DST测试工况均循环5次,每次循环包括14个步骤.图12给出了实验过程中锂离子电池的端电压和端电流. T/s(a)充电工况 T/s(b)放电工况 4.1 模型验证 将采集到的锂离子电池的电压和电流值代入到图10所示的模型中,分别得到两种工况下考虑滞回特性和不考虑滞回特性的锂离子电池端电压估计值及估计误差,如图13所示.从图13(c)可以看出,在DST工况下考虑滞回特性的端电压估计误差在0.02 V以内, 不考虑滞回特性的端电压估计误差最大达到0.06 V.说明二阶RC滞回模型在电流剧烈变化的情况下可以更准确地表现电池的动态特性. 4.2 算法验证 采用容积卡尔曼滤波估计电池SOC,实验结果如图14所示.通过图14(b)可以看出,考虑滞回特性时SOC估计误差在2%以内,说明基于二阶RC滞回模型的CKF算法,可以准确估计电池SOC.不考虑滞回特性时SOC估计误差仍在5%以内,说明即便电池模型偏差较大时,CKF算法仍能相对准确地跟踪实际值,表明CKF具有较好的鲁棒性. (a)电压实际值与估计值 (b)电压实际值与估计值局部放大 (c)端电压估计误差 (a)SOC实际值与估计值 (b)SOC估计误差 为了比较在SOC初始值不准确的情况下,EKF算法和CKF算法收敛至真值的速度,分别将充电工况和放电工况下的SOC初始值设置为0.4,0.6.实验结果如图15所示.可以看出CKF算法比EKF收敛速度更快,具有更好的动态抗扰性能. (a)SOC实际值与估计值 (b)SOC实际值与估计值局部放大 本文通过对锂离子电池的充放电实验,定量地分析了滞回特性对电池SOC估计的影响,建立了简单易行的锂离子电池等效滞回模型.同时,提出了基于容积卡尔曼滤波的电池SOC估计方法.最后,通过实验验证得到如下结论: 1)考虑滞回特性的锂离子二阶RC滞回模型较传统模型,能够更准确地模拟电池的动静态特性,可以适用于充放电电流快速变化的复杂工况,且易于工程实现; 2)在已建立的滞回模型的基础上,应用CKF 算法可以实现对电池 SOC 的高精度估计,即使在不考虑滞回特性的情况下,模型误差大,CKF 算法仍可以维持一定的精度,体现算法具有良好的鲁棒性. 本文的研究工作仍存在一些不足,主要包括: 1)建立的动态电路模型没有考虑温度的影响,但在实际应用中温度因素对电池的使用影响很大.因此,如果要更精确估计电池 SOC,必须考虑温度的影响; 2)实验过程中的测试对象均为单体电池,没有考虑复杂电池组的情况,电池组中单体电池的不一致也会影响到 SOC 的估计. 3)实验过程中没有考虑充放电对指挥特性的影响. [1] 蒋瑞斌, 谭理刚. 电动汽车的发展及面临的挑战[J]. 机械工程师,2009, 2: 23-25. JIANG Rui-bin, TAN Li-gang.The development and the challenges of electric vehicles[J]. Mechanical Engineer,2009, 2: 23-25.(In Chinese) [2] 谭晓军.电动汽车动力电池管理系统设计[M]. 广州:中山大学出版社,2011. TAN Xiao-jun. The design of electric vehicle power battery management system[M]. Guangzhou:SunYat-sen University Press, 2011. (In Chinese) [3] ALA Al-HAJ HUSSEIN, NASSER KUTKUT, ISSA BATARSEH. A hysteresis model for a lithium battery cell with improved transient response[C]//IEEE 2011 Applied Power Electronics Conference and Exposition (APEC).2011, 1790-1794. [4] HUSSEIN H A H, KUTKUT N, BATARSEH I. A hysteresis model for a lithium battery cell with improved transient response[C]//Applied Power Electronics Conference and Exposition (APEC), 2011 Twenty-Sixth Annual IEEE. IEEE, 2011: 1790-1794. [5] TRAPANESE M, FRANZITTA V, VIOLA A. The jiles atherton model for description of hysteresis in lithium battery[C]//Applied Power Electronics Conference and Exposition (APEC), 2013 Twenty-Eighth Annual IEEE. IEEE, 2013: 2773-2775. [6] ROSCHER M A, SAUER D U. Dynamic electric behavior and open-circuit-voltage modeling of LiFePO4-based lithium-ion secondary batteries[J]. Journal of Power Sources, 2011, 196(1): 331-336. [7] 田甜, 李孝尊, 李红梅.磷酸铁锂电池的改进建模及SOC估计[J]. 合肥工业大学学报:自然科学版, 2012(9): 1192-1195,1252. TIAN Tian, LI Xiao-zun, LI Hong-mei. Modified modeling and SOC estimation of LiFePO4 Li-ion battery[J]. Journal of Hefei University of Technology :Natural Science, 2012(9): 1192-1195,1252. (In Chinese) [8] BARONTI F, ZAMBONI W, FEMIA N,etal. Experimental analysis of open-circuit voltage hysteresis in lithium-iron-phosphate batteries[C]//Industrial Electronics Society, IECON 2013-39th Annual Conference of the IEEE. IEEE, 2013: 6728-6733. [9] EICHI H R, CHOW M Y. Modeling and analysis of battery hysteresis effects[C]//Energy Conversion Congress and Exposition (ECCE), 2012 IEEE. IEEE, 2012: 4479-4486. [10]JOHNSON V H. Battery performance models in advisor [J]. Journal of Power Sources,2002,110(2):321-329. [11]KROEZE R C, KREIN P T. Electrical battery model for use in dynamic electric vehicle simulations[C]//Power Electronics Specialists Conference. 2008. Pesc 2008. IEEE,2008:1336-1342. [12]王小旭, 潘泉, 黄鹤, 等. 非线性系统确定采样型滤波算法综述[J]. 控制与决策, 2012, 27(6): 801-812. WANG Xiao-xu, PAN Quan, HUANG He,etal. Overview of deterministic sampling filtering algorithms for nonlinear system[J]. Control and Decision, 2012, 27(6): 801-812. (In Chinese) Application of Equivalent Hysteresis Model in Estimaion of State of Charge of Lithium-ion Battery CHENG Ze,LV Ji-kao†, LIU Ji-guang, WANG Li (College of Electrical and Automation Engineering, Tianjin Univ, Tianjin 300072, China) The quick and accurate estimation of the state of charge (SOC) of lithium-ion battery is one of the key technologies of battery management system. In view of this nonlinear dynamic system of lithium battery, through the test and analysis of lithium-ion battery hysteresis characteristics, the second-order RC hysteresis model was established, and the cubature kalman filter algorithm was used to estimate the battery state of charge. The experiment results show that the battery model can essentially predict the dynamic hysteresis voltage behavior of the lithium-ion battery and cubature kalman filtering algorithm can maintain high accuracy in the estimation process. lithium-ion batteries; state of charge; hysteresis model; cubature kalman filter 1674-2974(2015)04-0063-08 2014-06-23 国家自然科学基金资助项目(61374122),National Natural Science Foundation of China(61374122) 程 泽(1959-),男,天津人,天津大学副教授,博士 †通讯联系人,E-mail:lvjikao@163.com TM912.1 A

2 锂离子电池等效电路模型
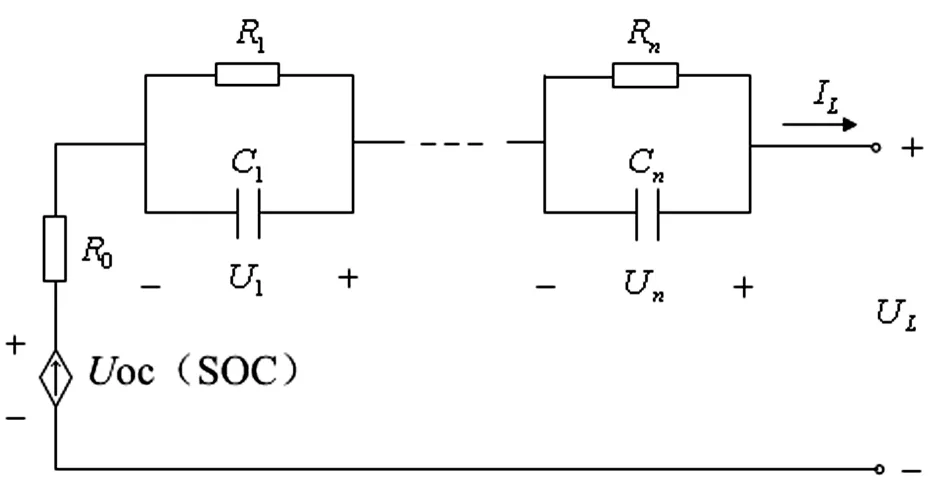
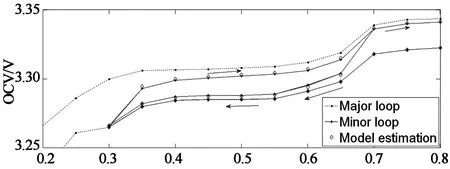
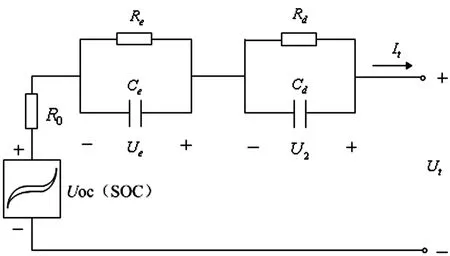

3 基于滞回特性的锂离子电池SOC估计

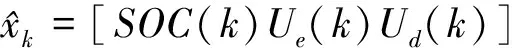

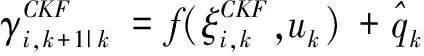


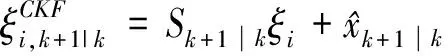
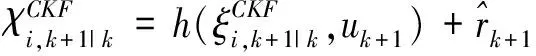




4 结果验证



5 结 论
