围岩收敛曲线形态对地下结构稳定系数影响分析*
2015-03-09苏永华
苏永华,付 雄,肖 旺
(湖南大学 土木工程学院,湖南 长沙 410082)
围岩收敛曲线形态对地下结构稳定系数影响分析*
苏永华†,付 雄,肖 旺
(湖南大学 土木工程学院,湖南 长沙 410082)
针对现代地下支护结构设计方法中缺乏物理意义明确的稳定性表征指标这一不完善之处,结合收敛-约束原理来开展研究.首先,通过选取基于Mohr-Coulomb失效准则的Kastner 公式和Duncan公式进行围岩弹塑性分析从而构建围岩收敛曲线;分析各支护单元的力学特性并构建锚喷支护结构支护特征曲线;然后,根据收敛-约束原理和荷载原理导出支护结构的稳定系数,从而建立不同围岩收敛曲线的地下结构稳定性定量评价方法;最后,在各岩体力学参数相似的条件下,通过算例分析不同围岩收敛曲线之间的差异性,展示了不同模式的操作和运行过程.
收敛-约束原理;围岩收敛曲线;稳定系数;差异性
地下结构不仅承受周边地层变形荷载,同时其受荷后变形又受到地层的约束.目前地下结构设计中,通常采用以经验围岩分级为主,以数值模拟得到其应力和应变分布为辅的设计方法,如《公路隧道设计规范》[1]等.这就导致了地下结构的设计方法及其稳定判断与地面结构的成熟性相比,还存在许多需要完善的方面.其中最主要的缺陷之一是没有类似于地面结构的安全系数对地下结构的稳定性进行定量评价.因此文献[2]提出了基于收敛-约束原理的稳定系数分析的思路与一般方法.该方法主要涉及到围岩收敛曲线和支护特征曲线.支护结构(多数以锚杆、喷射混凝土以及钢架等支护材料进行构建[3])为人工材料,其力学性质相对比较稳定,支护特征曲线的形态比较固定.由于岩体破坏模式、变形机制的复杂性,围岩收敛曲线则出现多样性,不同形态的曲线对分析结果可能不同.
从破坏模式而言,目前使用比较普遍的有Mohr-Coulomb(M-C)失效准则和Hoek-Brown (H-B)失效准则两大类;从变形机制而言,对于支护施工安装期间,隧道周边围岩主要有塑性剪胀和理想弹塑性两种表现.由于复杂性不可能全面考虑各种情况,同时也为了清楚地表达研究思路,在此着重分析在同一破坏模式下,考虑将围岩看做理想弹塑性材料及塑性剪胀材料时,确定的支护结构稳定性系数的差异.
基于上述目标,本文的研究思路是选用基于M-C准则的Kastner模式和Duncan-Fama模式作为代表,建立理想弹塑性及塑性剪胀围岩收敛曲线;采用串联准则建立锚喷结构的支护特征曲线;通过收敛-约束原理导出结构稳定性系数计算表达式;通过实例分析,对比分析不同曲线条件下结构稳定系数的差异.
1 围岩收敛曲线的构建
围岩收敛曲线是用来表征洞室开挖后洞壁所需的支护力与洞室周边位移之间关系的曲线[4-7],描述围岩地层对开挖的响应.本文选取基于M-C失效准则的Kastner理论及Duncan-Fama理论构建两类围岩收敛曲线.
1.1 理想弹塑性Kastner围岩收敛曲线
基于经典弹塑性理论的Kastner公式[4]给出了无限均匀介质中轴对称隧道周边位移与地层应力参数、地应力场和支护力之间的关系,可简化为二维平面应变问题.假定隧道无限长、原岩应力为p0,粘聚力为c,内摩擦角为φ,在不考虑体力的情形下,隧道弹塑性分析可视为轴对称问题[4]:
(1)
式中σr,σθ分别为径向应力和环向应力;p0,pi分别为原岩应力、支护压力;ri,re分别为隧道开挖半径、弹性区半径.当r=ri时,σr=pi;当r=re时,σr=σre;当r=∞时,σr=p0.屈服时的应力状态满足Mohr-Coulomb失效准则,即:
F=σθ-Nσr-σc=0
(2)
式中σc为岩体单轴抗压强度,其中N,σc的表达式分别为:
(3)
临界支护力picr作为围岩是否进入塑性状态的主要判据之一,picr可定义为:
(4)

(5)
式中E为围岩弹性模量,ν为泊松比.

(6)
1.2 考虑剪胀的Duncan-Fama围岩收敛曲线
(7)
式中M为弹塑性边界应力差,M=2p0sinφ+ 2ccosφ;各符号意义同前.
二者均基于M-C准则,然而与Kastner围岩收敛曲线相比,式(7)的Duncan-Fama收敛曲线考虑了剪胀现象,从机理上更接近围岩的力学机理与变形特性实质.
2 支护特征曲线
2.1 简 述
支护特征曲线是描述支护结构上所承受的支护压力与支护径向位移的关系曲线.作为支护结构最为典型的形式之一,锚喷支护具有多种组合型力学理论(经典弹塑性分析、组合拱理论、组合梁理论以及免压拱理论[8]),以圆形隧道为研究对象,假定围岩给予支护结构的反力是径向均匀分布的,此时混凝土衬砌或钢支撑的力学特性可认为是线弹性[9]的,可表述为:
p=ku
(8)
式中p,k,u分别为支护结构的支护力、刚度及径向位移.
2.2 喷射混凝土的支护特征函数
喷射混凝土作为柔性支护,在开挖半径为ri的圆形隧道下,当其厚度t较小时(t≤0.04ri),采用薄壁圆筒计算公式[10],其刚度ksh为:
(9)
式中Esh,νsh分别为喷射混凝土的弹性模量和泊松比.
ush,max为喷射混凝土层的极限径向位移,可表示为:
(10)
式中σsh为喷射混凝土层的单轴抗压强度,由此得喷射混凝土衬砌的支护特征函数为:
psh=ksh·ush(0 (11) 2.3 锚杆的支护特征函数 注浆的机械式锚杆或化学锚杆的刚度kb可用下式[11]确定: (12) 式中l,Eb,db分别为锚杆的长度、弹性模量、锚杆直径;sl,sc分别为沿隧道纵向和隧道轴向的锚杆间距,my为工作条件系数,取0.75~0.90.则锚杆的支护特征函数为: pb=kbub(0 (13) 2.4 锚喷联合支护的支护特征函数 在实际工程中,由于诸多因素的影响,采用多种支护单元联合成为支护体系且同时施作的施工方法较为普遍.则联合刚度kcon可表示为[12]: kcon=ksh+kb (14) 锚喷各个支护单元不产生破坏是保持锚喷联合支护结构稳定的前提.因此,锚喷支护的最大变形由极限变形最小的支护单元来决定,锚喷支护的支护特征函数为: (15) 隧道收敛-约束原理最早由Fenner提出,其基本思想为根据二维平面应变分析方式及采用计测的收敛资料,分析实际三维隧道开挖所引起围岩应力-位移变化和支护结构力学特性等问题[13]. 纵断面变形曲线是指开挖洞室未护支时洞壁径向位移沿洞室纵向的变化.而Hoek根据实际工程隧洞洞壁收敛位移的监测数据提出了如下的经验拟合公式[6]: (16) u0(u0=urx)为隧道开挖后支护前围岩产生的径向变形,ur∞为总收敛位移.根据原理简述图1可得:当围岩所产生的径向应力与支护结构提供的支护力达到平衡的时候(即平衡点),确定对应平衡点时支护结构所承受的压力peq,con,支护结构所能承受的容许抗力为plim,con,依据荷载原理推导出的支护结构的稳定系数Fc为: Fc=plim,con/peq,con (17) 图1 收敛-约束原理简述图 本文选取研究的工程实例为位于中国湖南省西部张家界市龙阳公路的梨子坪隧道.其位于湖南省张家界武陵源风景区,隧道全长3 225m,开挖断面为马蹄形,开挖高度为8.6m,最大跨度为11.6m,等代圆半径ri=5.05 m.根据地表地质地貌、隧道穿越岩层特征和隧道覆盖层厚度,取K10+120到K11+200段进行计算分析,隧道围岩等级Ш级,最大埋深为440 m左右.岩体力学参数如下:原岩应力σ1=σ2=σ3=σ0,求得σ0=11.924 MPa,岩块无侧限抗压强度σcm=10.04 MPa,弹性模量E=35 GPa,泊松比ν=0.29,粘聚力c=1.1 MPa,内摩擦角φ=44.46°,密度ρ=2.6 t/m3. 该段隧道支护采用锚喷支护,锚杆平均长度lb=3.0 m,直径db=22 mm,系统锚杆的纵向间距sl=2.0 m,轴向间距sc=1.0 m,弹性模量Eb=210×103MPa,工作系数取值my=0.75;喷混混凝土等级强度为C25,喷射厚度t=5 cm,弹性模量Esh=29.5 GPa,弯曲抗压强度σsh=24.2 MPa,泊松比νsh=0.15. 根据式(10)~(15)计算得喷射混凝土参数:ksh=298.80 MPa/m,ulim,sh=4.36 mm,plim,sh=1.350 MPa.锚杆参数:kb=10.74 MPa/m,plim,b= 0.167 MPa,ulim,b=15.595 mm;联合刚度kcon=309.54 MPa/m,极限承载力plim,con=1.350 MPa.根据式(16)计算得未支护前洞壁径向位移u0=4.07 mm. 根据收敛-约束图2以及相关计算原理分别求得Kastner公式和Duncan公式建立的支护结构稳定系数分别为1.67和1.62,得支护结构的稳定系数Fc均大于1.说明该支护结构处于稳定状态. 径向位移 5.1 参数取值 根据《公路隧道设计规范》,围岩分级时不同等级围岩岩体物理力学参数取值均有一定的范围[14],而Kastner公式及Duncan公式中,隧道周边位移与内摩擦角、粘聚力、变形模量以及泊松比等参数有关,因此本文选取内摩擦角、粘聚力、变形模量以及泊松比进行分析.其中变形模量G可由弹性模量E和泊松比ν表示为: (18) 5.2 差异分析 依据《公路隧道设计规范》中Ш级围岩力学参数取值范围(如表1),分析各力学参数在等级范围内变化时对稳定系数的影响,对比不同围岩收敛曲线计算稳定系数的差异性(注:以下收敛-约束图中K曲线代表Kastner曲线,D曲线代表Duncan曲线)对参数变化时两种稳定性系数进行差异分析,相对差异S表达式为: (19) 注:Fc,K,Fc,D分别为K法和D法所求的稳定系数. 表1 Ⅲ级围岩物理力学参数 采用两种围岩收敛曲线分析隧道周边位移分为两种情况:当pi≤picr时,围岩处于完全弹性状态,此时围岩保持自稳状态无需采取支护措施;当pi≥picr时,围岩进入弹塑性状态,此时需施设支护结构才能保持围岩的稳定.因此,下述分析仅考虑围岩进入弹塑性阶段时参数变化对稳定系数的影响. 如图3~4所示,虽然两者均基于M-C破坏准则,但是两者的适用性却有所差异.Kastner收敛曲线没有考虑围岩力学指标强度的变化,适用于理想弹塑性分析.而Duncan收敛曲线考虑了塑性区围岩力学参数的弱化及剪胀特征,其适用性显然要远远优于前者. 径向位移 径向位移 如图5~6及表2所示,Ⅲ级围岩中弹性模量变化对稳定性系数的影响最为显著,泊松比变化对稳定性系数的影响较小.但两种方法所求得的稳定系数差异较小,两者最大相对差异不超过20%.且Kastner法相对于Duncan法所得稳定系数均较大,这是由于采用Kastner法进行围岩弹塑性分析时,即便围岩进入塑性状态,塑性圈内的力学指标强度仍视为不变,各参数取值恒为常量;而Duncan法中当围岩进入弹塑性状态时,考虑了塑性圈内岩体发生破裂而导致其强度降低,各参数取值降低,力学参数取值变小后的围岩塑性区位移,其隧道周边位移显然大于Kastner法,根据对稳定系数的定义,分析得出稳定系数值显然小于Kastner法. 径向位移 径向位移 表2 参数不同值下的稳定性系数表 基于收敛-约束原理,选取同种失效准则的不同模式对开挖后的围岩进行弹塑性分析,结合地下工程中最为普遍的锚喷支护结构的支护特征曲线,提出了能定量描述地下结构稳定性的新计算方法.导出了具有明确物理意义的稳定性表征指标,取得了以下几方面研究成果: 1)考虑收敛-约束原理的主要因素,构建围岩收敛曲线和支护特征曲线,依据荷载原理导出了结构的稳定系数及建立了荷载确定的图示法. 2)对目前基于收敛-约束原理的地下结构稳定系数计算方法进行补充.通过工程实例的应用分析,展示了该方法的实现过程和运行程序. 3)通过论证描述了两种分析模式的核心思想及适用范围,不同岩体应根据具体情况选择合适的分析模式. 4)不同围岩收敛曲线结合同一支护特征曲线进而导出不同的结构稳定系数.分析了Ⅲ级围岩参数范围内两者稳定系数的变化,对比了各自稳定系数的差异性. [1] 中华人民共和国行业标准编写组.JTGD70-2004公路隧道设计规范[S].北京:人民交通出版社,2004:73-75. The Professional Standards Compilation Group of People Republic of China.JTGD70-2004 The code for design of highway tunnel[S].Beijing:China Communications Press, 2004:73-75.(In Chinese) [2] 苏永华,刘少峰,王凯旋.基于收敛-约束原理的地下结构稳定性分析[J].岩土工程学报,2014,36(11):2002-2009. SU Yong-hua,LIU Shao-feng,WANG Kai-xuan.Stability analysis means for underground structure in connection with the convergence-confinement method[J]. Journal of Geotechnical Engineering,2014,36(11):2002-2009.(In Chinese) [3] 苏永华,梁斌,伍文国.越岭浅埋偏压隧道支护系统承载特性分析[J].湖南大学学报:自然科学版,2012, 39(2):1-6. SU Yong-hua,LIANG Bin,WU Wen-guo.Analysis on loa-ding characteristics of supporting system of the servants and shallow tunnel under asymmetrical pressure[J]. Journal Hunan University: Natural Sciences,2012,39(2):1-6.(In Chinese) [4] KITAGAWA T, KUMETA T, ICHIZYO T,etal. Application of convergence-confinement analysis to the study of preceding displacement of a squeezing rock tunnel[J]. Rock Mechanics and Rock Engineering, 1991, 24(1): 31-51. [5] DUNCAN-FAMA M E. Numerical modelling of yield zones in weak rock in comprehensive rock engineering[M]. UK:Oxford, Pergamon Press, 1993:49-75. [6] CARRANZA-TORRES C, FAIRHURST C.Application of the conver-gence-confinement method of tunnel design to rock mass satisfy the Hoek-Brown failure criterion[J]. Tunnelling and Underground Spacen Technology,2000, 15(2): 187-213. [7] 姚国圣, 李镜培,谷拴成.考虑岩体扩容和塑性软化的软岩巷道变形解析[J].岩土力学,2009,30(2):463-467. YAO,Guo-sheng,LI Jing-pei,GU,Shuan-cheng.Analytic solution to deformation of soft rock tunnel consideringn dilatancy and plastic softening of rock mass[J]. Rock and Soil Mechanics,2009,30(2):463-467.(In Chinese) [8] 唐雄俊. 隧道收敛约束法的理论研究与应用[D]. 武汉:华中科技大学土木工程学院, 2009:25-73. TANG Xiong-jun. Study on the convergence-confinement method and its application in tunnel construction[D].Wuhan:Civil Engineering and Mechanics College,Huazhong University of Science and Technology,2009:25-73.(In Chinese) [9] 孙闯,张向东,李永靖.高应力软岩巷道围岩与支护结构相互作用分析[J]. 岩土力学,2013,34(9):2601-2608. SUN Chuang,ZHANG Xiang-dong,LI Yong-jing.Analysis of interaction between surrounding rock and support structure in high stressed soft rock roadway[J]. Rock and Soil Mechanics,2013,34(9):2601-2608.(In Chinese) [10]苏永华,李翔,徐能雄,等.锚喷衬砌隧道结构稳定可靠度计算[J].土木工程学报,2011,44(3): 113-119. SU Yong-hua,LI Xiang, XU Neng-xiong,etal.Calculation calculation of reliability for the structural stability of tunnel linings consisting of rock-bolts and shotcrete consisting of rockbolts and shotcrete[J].Journal of Civil Engineering,2011,44(3): 113-119.(In Chinese) [11]李志业,曾艳华.地下结构设计原理与方法[M]. 成都:西南交通大学出版社, 2003:23-75. LI Zhi-ye ZENG Yan-hua.Design principle and method of underground structures[M].Chengdu:Southwest Jiaotong University Press,2003:23-75.(In Chinese) [12]ORESTE P.Analysis of structural interaction in tunnel using the covergence-confinement approach[J]. Tunnelling and Underground Space Technology, 2003,18(4): 347-363. [13]李煜舲, 许文贵, 林铭益. 以隧道变形量测资料分析掘进效应与约束损失[J].岩石力学与工程学报, 2009,28(1):39-46. LI Yu-lin,XU Wen-gui,LIN Ming-yi. Analysis of advancing effect and confinement loss by using deformation measurements in tunnel[J]. Chinese Journal of Rock Mechanics and Engineering,2009,28(1):39-46.(In Chinese) [14]苏永华,常伟涛,赵明华.深部巷道围岩稳定的区间非概率指标分析[J].湖南大学学报:自然科学版,2007,34(7):17-21. SU Yong-hua,CHANG Wei-tao, ZHAO Ming-hua.Nonprobabilistic index analysis method of the stability of deep-rock around road-way based on interval variable[J].Journal of Hunan University: Natural Sciences,2007,34(7):17-21.(In Chinese) The Analysis for Stability Coefficient of Underground Structure with the Shapes of Ground Response Curves SU Yong-hua†, FU Xiong, XIAO Wang (Collge of Civil Engineering, Hunan Univ, Changsha,Hunan 410082, China) To address the deficiencies of new design methods of underground supporting structure, which lacks stability index of definite physical meanings, a study was conducted with the convergence-confinement theory. First the Kastner formula and the Duncan formula based on the Mohr-Coulomb failure criterion were selected to analyze the elastic-plastic of rock to establish ground characteristic curve. Each support unit was analyzed in series to establish the support characteristic curve of bolt-shotcrete support structure. Then, the stability coefficient of the support structure was derived in accordance with the principle of convergence-confinement and the principle of loat, which build up the quantitative evaluation of the stability of underground structure method for different stratigraphic characteristic curves. Finally, the otherness between different ground characteristic curves was demonstrated by other examples under similar conditions for rock mass mechanical parameters. Different modes of operations and operation processes were also shown. convergence-confinement theory;ground response curve;stability coefficient;otherness 1674-2974(2015)07-0087-06 2014-10-17 国家自然科学基金资助项目(51378195, 51078136), National Natural Science Foundation of China(51378195, 51078136) 苏永华(1966-),男,湖南涟源人,湖南大学教授,博士 †通讯联系人,E-mail:yong_su1965@126.com TU 458 A3 基于收敛-约束法的结构稳定系数
4 工程实例分析
5 对比分析




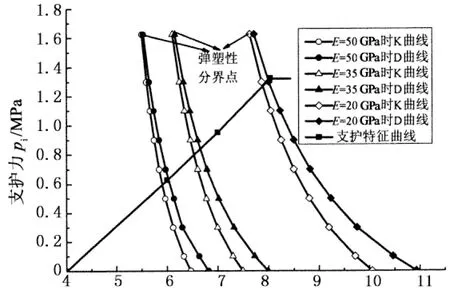
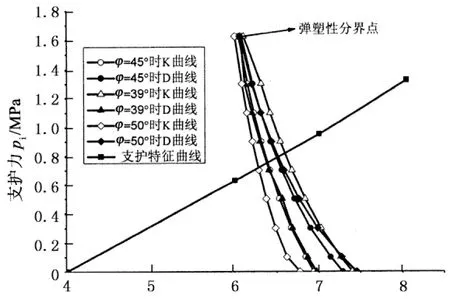
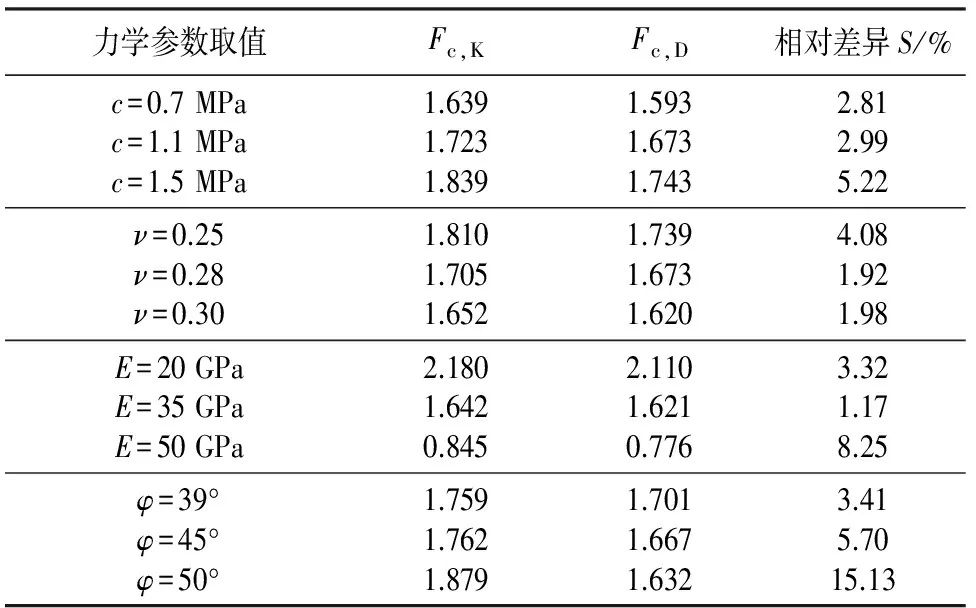
6 结 论
