无粘结部分预应力混凝土梁非线性全过程滞回分析*

唐昌辉,倪 佳，叶 林

(1.湖南大学 土木工程学院，湖南 长沙 410082；2. 中机十院国际工程有限公司，河南 洛阳 471003)

无粘结部分预应力混凝土梁非线性全过程滞回分析*

唐昌辉1†,倪 佳1，叶 林2

(1.湖南大学 土木工程学院，湖南 长沙 410082；2. 中机十院国际工程有限公司，河南 洛阳 471003)

在已完成的16根无粘结部分预应力混凝土梁低周反复荷载试验的基础上，合理地选择了各材料的本构关系模型，深入分析了无粘结部分预应力混凝土梁的受力特性，通过设置刚性短臂将无粘结预应力筋的作用等效为外荷载，综合运用“分级加变形”和“分级加荷载”的方法，提出了无粘结部分预应力混凝土梁的非线性全过程滞回分析方法，编制了MATLAB计算程序．对比试验结果与计算结果，吻合程度良好，具有一定的理论和工程意义.

无粘结部分预应力混凝土梁；低周反复荷载；非线性；滞回曲线；数值计算

无粘结部分预应力混凝土结构与其它配筋混凝土结构相比，其最大的特点是无粘结预应力筋与周围混凝土之间可以产生相对滑动，无粘结预应力筋的应力与结构或构件的整体变形相关，这就使其计算分析变得较为复杂.另外，低周反复荷载作用下的无粘结部分预应力混凝土梁，当变形较大时，无粘结预应力筋的线型会随着梁的整体变形而改变，其受力状态也会随之改变.本文在深入分析了无粘结部分预应力混凝土梁的受力特性之后，提出了一种基于结构整体变形协调条件的无粘结部分预应力混凝土梁非线性全过程滞回分析方法.

1 基本假定及本构关系

1.1 基本假定

1) 除无粘结筋外，满足平截面假定；

2) 各种材料均为单向受力状态；

3) 忽略无粘结预应力筋与混凝土之间的摩擦.

1.2 本构关系

1.2.1 混凝土本构关系

本文采用苏小卒提出的反复荷载作用下混凝土的本构关系，该本构关系综合了朱伯龙等的裂面效应模型以及Kent和Park、Blakeley和Park的混凝土本构关系模型，并且加卸载路径比较简单[1].在这个模型的基础上，加入混凝土受拉应力—应变骨架全曲线，并结合文献[2]中对混凝土本构关系相关参数的回归计算，得到一个新的反复荷载作用下的混凝土本构关系模型，如图1所示.为符合一般习惯，在本构关系的叙述中，混凝土的应力、应变符号以受压为正，其余各材料及程序中的混凝土应力、应变均以受拉为正.

图1 混凝土本构关系

骨架曲线.混凝土初始受压骨架曲线为OBCDE，初始受拉骨架曲线为OLM，则初始骨架曲线的应力—应变方程如式(1)所示：

(1)

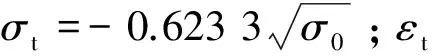
(2)

式中

(3)

(4)

在以上两式中，ρs为横向钢筋的体积配筋率，bcor为核心混凝土的宽度，S为箍筋间距.参数z的值反映了混凝土受箍筋约束的程度.

记εmax,εmin为历史上达到过的最大、最小应变;σmax,σmin为与εmax,εmin对应的初始骨架曲线上的应力.当ε>εmax或ε<εmin时，按初始骨架曲线计算应力.当εmin≤ε≤εmax时，如果εmin≥εt，则骨架曲线为直线HL和直线LA；如果εmin<εt，则将骨架曲线改为直线GK和直线KF，FJ.其中F点的应变为开始产生裂缝效应的应变，用εW表示，其表达式为：

(5)

加卸载路径.混凝土加卸载的路径均取为斜率为Ec的直线，但应力的绝对值不得超过骨架曲线上相应应变的应力绝对值，否则按照相应的骨架曲线表达式来计算混凝土的应力.当εmax>ε0时考虑混凝土弹性模量退化，Ec取值如式(6)所示：

(6)

1.2.2 普通钢筋及无粘结预应力筋本构关系

图2 普通钢筋本构关系

无粘结预应力筋的本构关系骨架曲线采用文献[2]中的建议，加卸载路径的斜率取直线段的斜率,如图3所示.

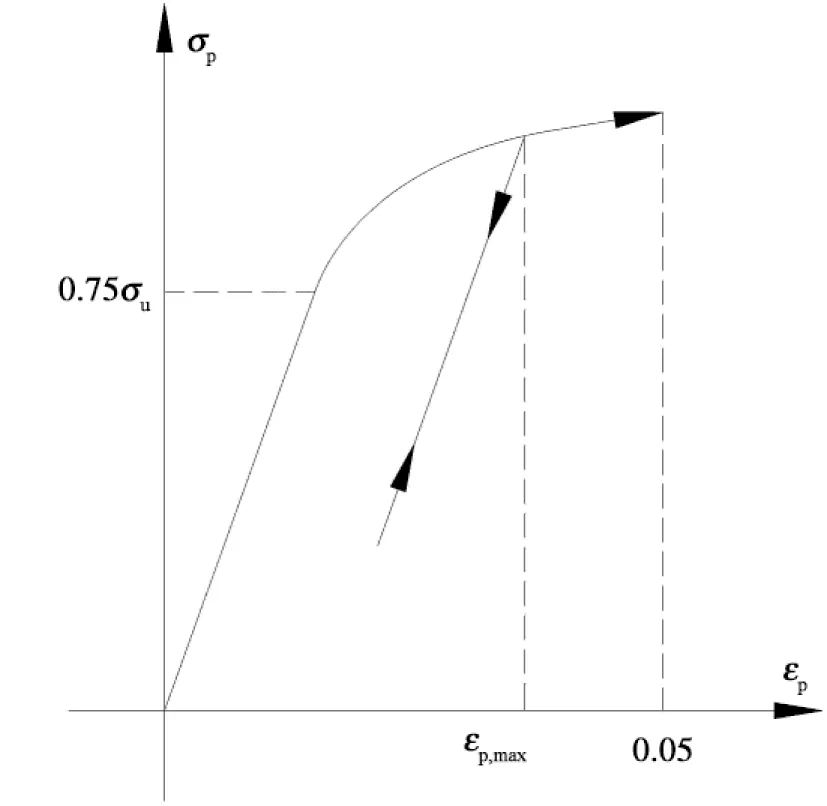
图3 无粘结预应力筋本构关系

2 单元划分及受力分析

混凝土采用全截面平均划分条带的方法，普通钢筋单独划分条带，如图4所示[3].

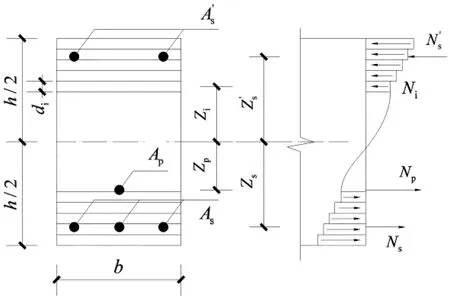
图4 矩形截面条带划分

(7)

(8)

在进行非线性分析时，将梁沿长度方向从支座至跨中将梁等分为n段，共n+1个截面，其中跨中、集中力作用点和支座处必须划分截面，如图5所示.无粘结预应力筋通过设置一个刚性短臂与梁联结起来，刚性短臂一端固定在截面参考轴线处，可传递力和弯矩，另一端与无粘结预应力筋联结并可自由滑动，如图6所示，参考轴线一般选取截面几何形心轴[4-5].这样处理的结果实际上是将连续光滑的无粘结预应力筋线型简化为多折线线型，将垂直于无粘结预应力筋形心轴的连续反力简化为多个集中反力，如图7所示，从而能够比较简单地获得等效荷载.

图5 梁长度方向单元划分

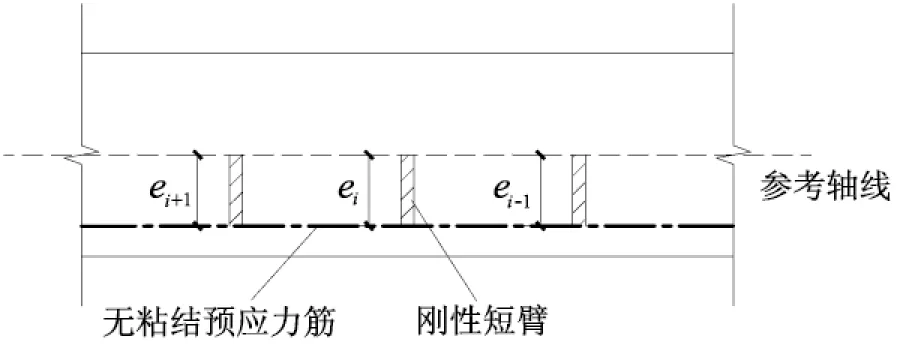
图6 无粘结预应力筋与梁的联结

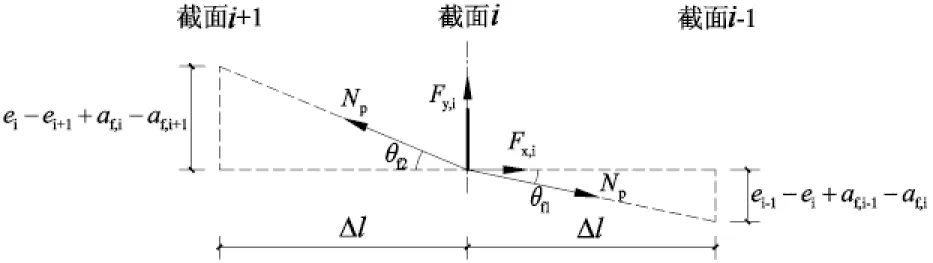
图7 无粘结预应力筋作用的等效

在计算过程中，无粘结预应力筋的作用等效为一个端部合力Np和作用于各个刚性短臂的分力Fx,,Fy,i，如图7所示，其中

(9)

(10)

(11)

式中ei为i截面处无粘结预应力筋的偏心距;af,i为i截面的挠度;Δl为单元长度;Np为假定的无粘结预应力;θf1,θf2可根据图中几何关系求得;Fx,i,Fy,i以图7所示方向为正反向.对于本文的计算对象来说，当等效分力较大时，截面倾角θi很小；当等效分力很小时，截面倾角θi相对较大.因此本文在计算等效分力时忽略了截面倾角的影响，但对于端部合力Np，截面n的倾角θn不可忽略.

分析时对梁跨中截面分级加曲率，假定无粘结预应力筋合力Np和各个截面的挠度af,i，根据上述方法很容易求得各个截面的轴力Ni.

(12)

已知跨中截面的曲率和轴力，可以求得对应的跨中截面弯矩M0，取跨中截面左侧为隔离体，如图8所示，由力和弯矩的平衡条件可得：

(13)

-0.5P1l1+P2(0.5l1+l2)-(0.5l1+l2)Npsinθn+

(14)

式中xi,0为i截面到跨中截面的距离.联立式(13)和(14)，即可解得外荷载P1和支座反力P2.对无粘结预应力筋来说，实际受力平衡，考虑到计算中其受力为等效荷载反力，所以有

(15)

同理，从跨中算起第i截面的弯矩为：

Mi=

(16)

式中xp1,i,xp2,i为力P1,P2作用点到i截面的距离；xk,i为k截面到i截面的距离.

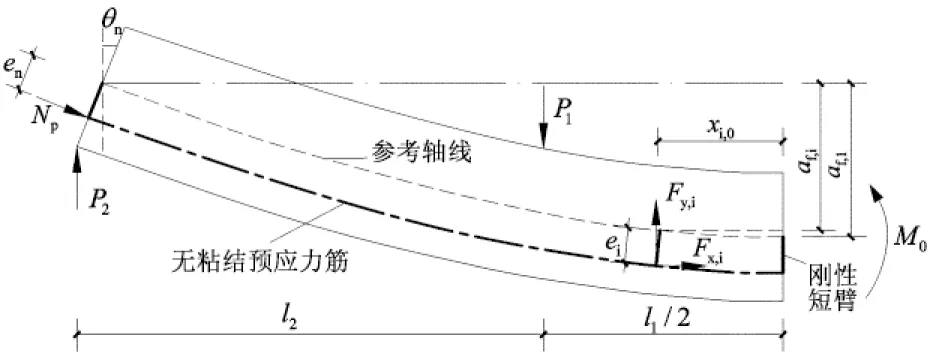
图8 跨中截面左侧隔离体

然后利用曲率微分法，如图9所示，根据式(17),(18)，采用数值积分的方法可求得各个截面的新的倾角和挠度[6]:

(17)

(18)

图9 无粘结预应力筋作用的等效

3 滞回计算过程

3.1 分析步骤及计算框图

无粘结部分预应力混凝土梁的非线性全过程滞回分析按下列步骤进行，计算框图如图10所示：

图10 计算框图

1)计算有效预应力作用下梁各截面的曲率、挠度等初始状态；

2)在初始状态基础上，每次取梁跨中截面曲率φ0为φ0=φ0+Δφ0；

3)假设无粘结部分预应力混凝土梁的挠度af,i，及相应的挠曲线；

4)假设无粘结预应力筋的合力为Np；

5)根据梁的受力状态，计算跨中截面的弯矩M0；

6)判断并处理塑性变形区域；

7)计算出其它截面的弯矩Mi；

9)计算各截面无粘结预应力筋周围混凝土的应变，叠加求平均值，得到满足变形协调条件的无粘结预应力筋合力Ncal；

10)采用二分法调整假定的无粘结预应力筋合力Np，重复步骤4)～9)，直到|Np-Ncal|满足精度条件为止；

11)计算各截面的挠度，得到新的挠曲线，即相应的挠度af1,i，如果跨中截面的挠度差值不满足精度要求，用新的挠曲线代替原挠曲线，重复步骤3)～10)；

12) 如果跨中截面的挠度差值满足精度要求，更新有关变量，重复步骤2)～11)，直到完成加载.

在上述步骤中，为减少迭代试算次数，从第3次加载开始，步骤3)中假定的无粘结预应力筋合力Np取上次加载完成后Np的值与前两次加载完成后Np的差值之和.实际上，跨中截面的求解为“分级加变形”的方法，其余各截面的求解为“分级加荷载”的方法.

对于单个截面来说，采用分级加荷载的方法求下降段很困难.但是对于整个构件来说，由于跨中截面采用的是分级加变形的方法，可以方便地求出下降段，当跨中截面的承载力开始下降时，其余截面实际处于卸载状态，并没有进入下降段.

3.2 塑性变形区的处理

文献[7]根据前人对钢筋混凝土梁和预应力混凝土梁进行的试验和理论研究，提出了无粘结部分预应力混凝土梁的跨高比分析模型.作者认为，当无粘结部分预应力混凝土梁达到极限状态时，沿梁长度方向的截面曲率分布应当如图11中的实线所示，这样才能考虑弯剪区段内斜拉裂缝的影响，图中虚线为纯受弯时的曲率分布情况.在进行非线性分析时，la=l0+dp范围内的截面受力状态相同，其余区段内的曲率可通过非线性分析求得，dp为无粘结预应力筋截面形心到梁截面上边缘的距离.

图11 极限状态时梁的裂缝形态及曲率分布

综合相关文献的研究成果，并结合文献[2]试验和编程的具体情况，在本文的分析中，当无粘结部分预应力混凝土梁跨中截面曲率φ达到极限曲率φu时，塑性变形区的长度取为2h/3+a，其中h为截面高度，a为纯弯段长度；当梁跨中截面曲率φ小于或者等于屈服曲率φy时，塑性变形区长度取为0；当φy<φ<φu时，按线性内插法取值.除塑性变形区长度的处理方法外，对塑性变形区还做了如下处理：

2)在卸载和反向加载时，塑性变形区的长度保持不变.

4 计算结果与试验结果的对比

M-φ滞回曲线和M-af滞回曲线计算结果和试验结果的对比分别如图12、图13所示.

图12 M-φ滞回曲线对比

图13 M-af 滞回曲线对比

从图12和图13中可以看出，计算结果与试验结果吻合较好.由于没有考虑普通钢筋与混凝土之间的粘结滑移[8]，滞回曲线的滑移段误差较大；开始卸载时的变形滞后现象难以模拟，造成卸载刚度有一定的误差.从整体来看，计算结果的规律无粘结部分预应力混凝土梁的滞回特点基本相同，说明本文的非线性全过程分析方法是可行的、合理的.

5 结 论

在基本假定的基础上，合理选取各材料的本构关系模型，对梁截面和长度方向进行单元划分并进行受力分析，通过刚性短臂将无粘结预应力筋的作用等效为外荷载，考虑塑性变形区的影响，给出无粘结部分预应力混凝土梁非线性全过程滞回分析的详细步骤和计算框图.并与试验结果对比，验证分析方法和程序的合理性和正确性，且具有一定的理论和工程实际意义.

[1] 苏小卒.预应力混凝土框架抗震性能研究[M].上海:上海科学技术出版社,1998: 62-64.

SUXiao-zu.Studyofseismicperformancesonprestressedconcreteframe[M].Shanghai:ShanghaiScienceandTechnologyPress, 1998:62-64.(InChinese)

[2] 唐昌辉.无粘结预应力混凝土梁和型钢混凝土柱的试验与研究[D]. 长沙:湖南大学土木工程学院,2003:18-30,95-98.

TANGChang-hui.Experimentsandresearchesonunbondprestressedconcretebeamsandsteelreinforcedconcretecolumns[D].Changsha:CollegeofCivilEngineering,HunanUniversity,2003: 18-30,95-98.(InChinese)

[3] 朱伯龙,董振祥.钢筋混凝土非线性分析[M].上海:同济大学出版社,1985:42-93.

ZHUBo-long,DONGZhen-xiang．Nonlinearanalysisofreinforcedconcrete[M].Shanghai:TongjiUniversityPress, 1985:42-93.(InChinese)

[4]ARIYAWARDENAN,GHALIA.Prestressingwithunbondedinternalorexternaltendons:Analysisandcomputermodel[J].JournalofStructuralEngineering,ASCE, 2002, 128(12): 1493-1501.

[5] 房贞政.无粘结预应力混凝土结构开裂后的弯曲分析[J].福州大学学报,1988,28(4):55-65.

FANGZhen-zheng.Bendinganalysisofunbondedprestressedconcretestructuresaftercraking[J].JournalofFuzhouUniversity,1988,28(4):55-65.(InChinese)

[6] 沈聚敏,翁义军.钢筋混凝土构件的变形和延性[J].建筑结构学报,1980,1(2):47-58.

SHENJu-min,WENGYi-jun.Thedeformationandductilityofthereinforcedconcretemembers[J].JournalofBuildingStructures, 1980,1(2):47-58.(InChinese)

[7]HARAJLIMH,HIJAZISA.Evaluationoftheultimatesteelstressinpartiallyprestressedconcretemembers[J].PCIJournal, 1991, 36(1): 62-82.

[8] 朱伯龙,吴明舜,张昆联.在周期荷载作用下钢筋混凝土构件滞回曲线考虑裂面接触效应的研究[J].同济大学学报,1980,8(1):63-75.

ZHUBo-long,WUMing-shun,ZHANGKun-lian.Astudyofhystereticcurveofreinforcedconcretemembersundercyclicloadingtakingaccountoflocalcontacteffectsofcrackedsection[J].JournalofTongjiUniversity, 1980,8(1):63-75.(InChinese)

Nonlinear Full Range Hysteretic Analysis on Unbonded Partially Prestressed Concrete Beams

TANG Chang-hui1†, NI Jia1,YE Lin2

(1.College of Civil Engineering, Hunan Univ, Changsha, Hunan 410082, China;2.TDI International Engineering Company Co Ltd, Luoyang, Henan 471003, China)

Based on the tests of sixteen unbonded partially prestressed concrete beams under low cyclic reversed loading, the constitutive relations under cyclic loadings of every material were selected reasonably. After an in-depth analysis on the mechanical characteristics of unbonded partially prestressed concrete beams, unbonded prestress actions were converted to their equivalent loads by setting short rigid arms. Then, a nonlinear full range hysteretic analysis method for unbonded partially prestressed concrete beams was proposed by combining the step deforming method and the step loading method, and a MATLAB program was developed. Through comparisons and analyses, the calculated results coincide well with the testing results. So it has theoretical and practical engineering significance.

unbonded prestressed concrete beams; low cyclic loading; nonlinear; hysteretic loops; numerical method

1674-2974(2015)07-0062-07

2014-12-09

国家自然科学基金资助项目(50978091),National Natural Science Foundation of China(50978091)

唐昌辉(1964-)，男，湖南新宁人，湖南大学副教授，博士

†通讯联系人，E-mail: tchui2010@126.com

TU378.2

A