支持向量机在轴承故障识别中的应用研究

Research on the Application of Support Vector Machine in Fault Recognition of Bearings

孙小权　邹丽英

(浙江工业大学之江学院,浙江 杭州　310024)

支持向量机在轴承故障识别中的应用研究

Research on the Application of Support Vector Machine in Fault Recognition of Bearings

孙小权邹丽英

(浙江工业大学之江学院,浙江 杭州310024)

摘要：滚动轴承的运行状态直接影响机械设备的正常运行。为及时准确识别滚动轴承的运行状态，通过对滚动轴承运行过程中的振动信号分析，采用小波包变换提取各频带内的能量熵，以此作为反映轴承运行状态的特征向量，并利用支持向量机对提取的特征向量进行模式识别。研究结果表明，支持向量机的轴承故障识别准确率均达到99%以上，而采用多项式核函数的支持向量机识别准确率最高，可达99.6%。

关键词：滚动轴承故障识别小波包能量熵特征向量支持向量机

Abstract：The running status of rolling bearings directly affect the normal operation of machinery and equipment, in order to precisely recognize the running status of rolling bearings, through analyzing the vibration signals during the running process of rolling bearings, by adopting wavelet packet transform method to extract the energy entropy in each frequency band, which reflects the feature vector of the running status, and by using support vector machine, the pattern recognition for feature vector extracted is conducted. The result of research indicates that the accurate rate of this method is above 99%, while the highest recognition accuracy by using polynomial kernel function support vector machine is 99.6%.

Keywords：Rolling bearingFault recognitionWavelet packetEnergy entropyFeature vectorSupport vector machine

0引言

随着科学技术的发展，机械设备在现代工业生产中的作用和影响越来越大，其产生的相关费用也越来越高。此外，机械设备运行过程中发生的任何故障或失效不仅会造成重大的经济损失，甚至造成人员伤亡。检测设备工况，及时发现故障，减小故障范围，尽可能地减小故障造成的损失是机械工程领域普遍关注的课题。

滚动轴承是旋转机械最重要的组成部件, 其运行状态是否正常直接影响整个机械性能，但滚动轴承是机械部件中最易损坏的零件。滚动轴承的状态一般可分为四种：正常、滚动体故障、内圈故障和外圈故障。不同状态之间时域信号差异性小，难以准确及时识别。当发生故障时，各个频段的信号能量会发生变化，其包含了丰富的故障信息。将各频段上的能量值作为特征向量，利用支持向量机的分类优势识别故障，实现轴承故障的智能化诊断[1]。

1状态特征提取

小波变换可以将时域信号分解为不同频段上的时域信号。但小波变换在逐层分解时仅对低频段进行分解，而在轴承故障检测中，不同的故障主成分存在不同的频段。为了能准确提取不同的故障特征，需要在全频段上进行逐层分解。小波包变换就能实现这一要求。小波包变换的每层分解都是在高低频段同时进行。小波包转换的结果就是得到多个频段上的分解系数，即小波包系数。对这一系数进行信号重构就可得到不同频段上的时域信号[2]。三层小波包分解如图1所示。

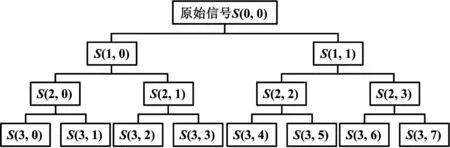
图1　三层小波包分解

仅用不同频段上的时域信号还是不能准确识别故障类型。当轴承出现故障时，对各频段内的信号能量会产生较大的影响，根据不同频段内的能量分布就可以识别出相应的故障类型。反映信号能量的参数可以选择频段内信号的平方和，也可以选择频段内信号的标准差或者其他一些算法。Matlab中提供了Wentropy函数，有多个能量熵类型可供选择。当信号进行三层小波包分解并对分解系数进行重构后，就可以得到八个频带上的能量信号Ei，从而构成能量特征向量E=[E0E1… E7]，归一化后作为支持向量机的输入向量。

2运行状态识别

2.1　支持向量机

支持向量机[4]是在统计学习理论基础上发展起来的一种新的机器学习方法，能解决小样本、维数灾难、过学习等问题。支持向量机以构造最优超平面为目标，将不可分的数据映射到高维特征空间中，在高维特征空间中正确区分各类样本。

设有两类线性可分的样本集合：

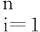
(1)

它可以被一个最优分类超平面(如式(3)所示)没有错误地分开，并且离超平面最近的向量与超平面的距离是最大的。

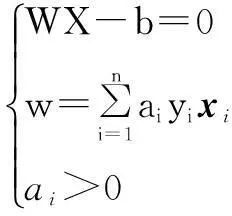
(2)

最优分类面函数为：

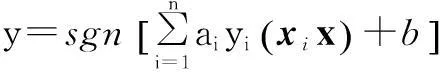
(3)

式中：xi为支持向量；ai为对应的拉格朗日系数；b为分类阈值。

二维线性可分的最优分类图如图2所示。图2中, 方形点和圆形点代表两类样本,H为分类线,H1、H2分别为过各类中离分类线最近的样本且平行于分类线的直线。margin=2‖w‖为H1和H2之间的间隔，其中w为分类线的权重向量，‖*‖为欧式模。

图2　二维线性可分的最优分类线

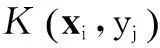
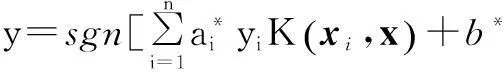
(4)

常用的一些核函数如下。

① q 次多项式函数：

(5)

② 径向基函数：

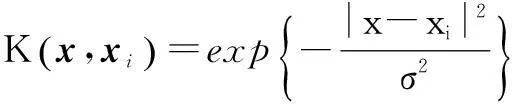
(6)

③ Sigmoid函数：

(7)

式(4)的支持向量机分类函数在形式上类似于一个神经网络，输出S个中间节点的线性组合，每个中间节点对应一个支持向量，如图3所示。

图3　支持向量机示意图

由于最终的判别函数中实际只包含未知向量与支持向量内积的线性组合，因此识别时的计算复杂度取决于支持向量的个数。

支持向量机最初是针对二分类问题的，当用于多分类问题时，可以以二分类为基础，构造多个二类分类器。通过求解多个分类器的分类超平面，获得分类问题的最优解。

2.2　支持向量机参数优化

使用训练集建立支持向量机模型需要根据数据特征向量选择合适的核函数和相关参数。径向基函数应用较广泛，可以适应大多数的应用场合。径向基核函数需要设置两个参数，分别是核函数的宽度参数g和误差惩罚系数c。g主要影响数据在高维空间中分布的复杂程度，c是在特定空间中调节学习机的置信范围和经验风险的比例。合适的参数可以通过多种方法进行寻优得到，如网格算法、遗传算法、粒子群算法等。

3实例分析

本试验数据来自美国Case Western Reserve University 电气工程实验室，该数据是在滚动轴承故障模拟实验台上测量得到[5]，采样频率为12 kHz。轴承的损伤是用电火花加工的单点损伤。损伤直径分为0.177 8 mm、0.355 6 mm、0.533 4 mm、0.711 2 mm、1.016 mm五种，分别针对外滚道损伤、内滚道损伤、滚动体损伤。外滚道损伤分别在时钟的3点、6点、12点三个不同位置进行设置。为便于分析，本实例选择六种状态(正常、内圈故障、滚动体故障、外圈3故障、外圈6故障、外圈12故障)的数据进行分析，样本数据如表1所示。

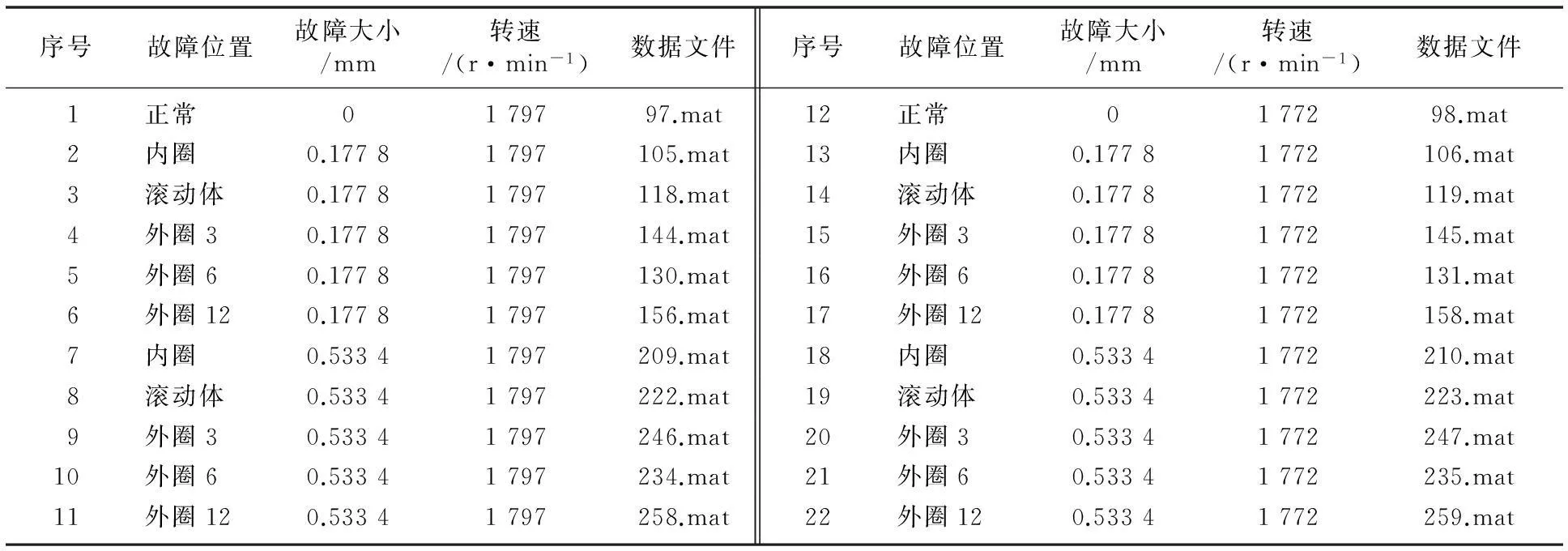
表1　分析样本数据

3.1　特征提取

分别对上述数据按1 024个采样数据作为一个样本，进行三层小波包变换，并重构三层小波包分解系数，得到八组不同频段的时域信号，如图4所示，对分解后的八组数据分别求能量熵，得到一组八维的特征向量。对这一特征向量进行归一化处理，作为支持向量机的输入向量。图4中，S0为原始信号，S1～S8分别为八个频段上的时域信号。

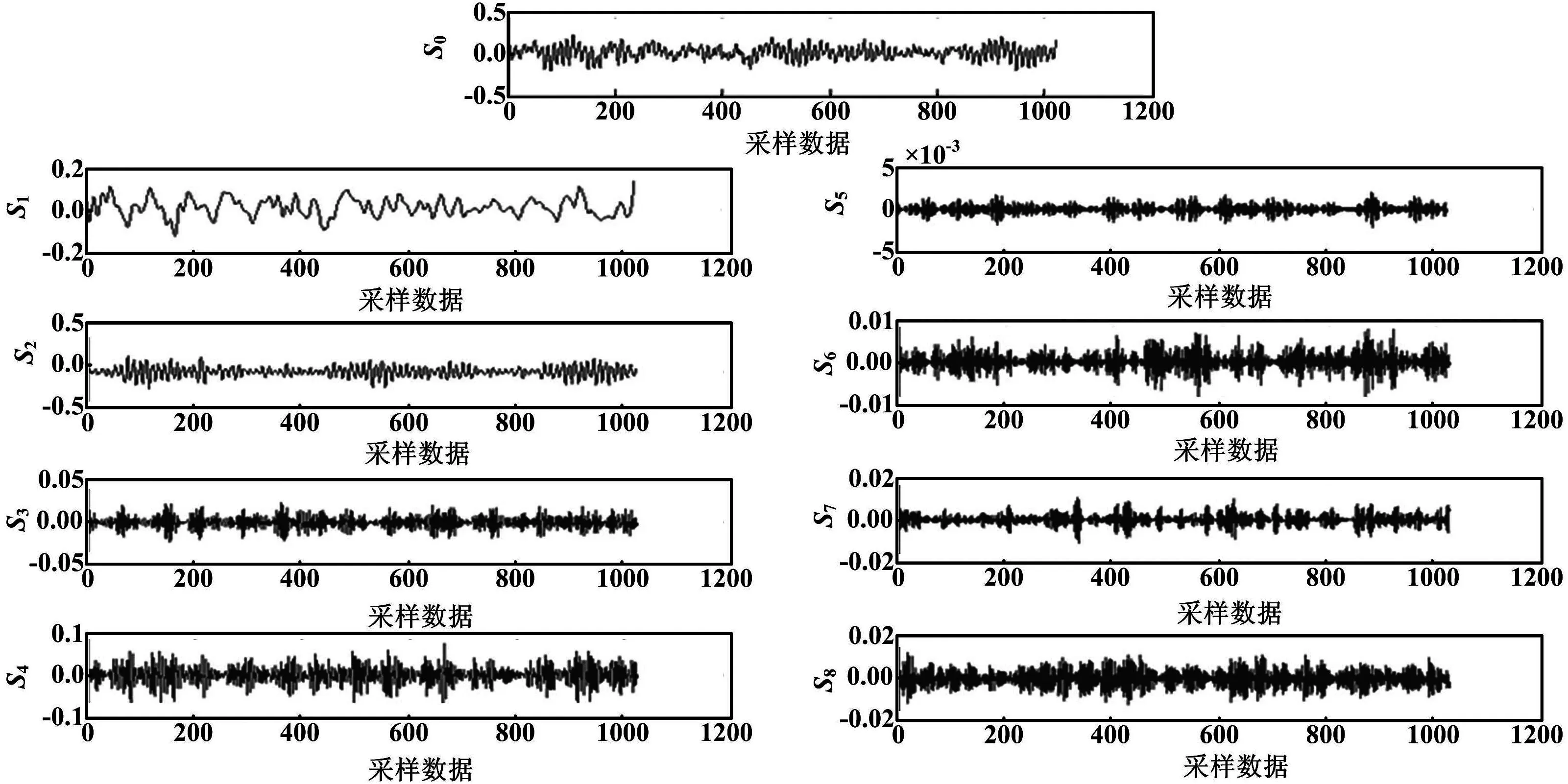
图4　三层小波包分解重构信号

3.2　训练与识别

经过上述处理，得到若干组六种状态下的能量熵数据，将每种状态的50%的数据作为训练样本，另一半作为分类测试。当核函数选用径向基函数时，采用网格寻优法得到最佳参数g=64、c=1， 最佳交叉验证准确率达到99.887 1%。

网格寻优图如图5所示。

图5　网格寻优图

当核函数选用线性或多项式函数时，所得到的交叉验证准确率分别达到99.21%和99.94%。使用优化后的参数建立支持向量机模型，并对测试数据进行分类测试，常用的几类核函数测试结果如表2和表3所示。

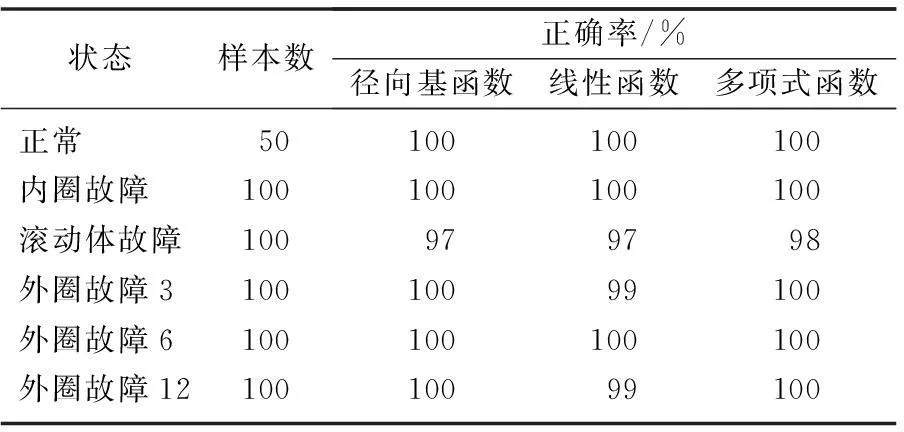
状态样本数正确率/%径向基函数线性函数多项式函数正常50100100100内圈故障100100100100滚动体故障100979798外圈故障310010099100外圈故障6100100100100外圈故障1210010099100

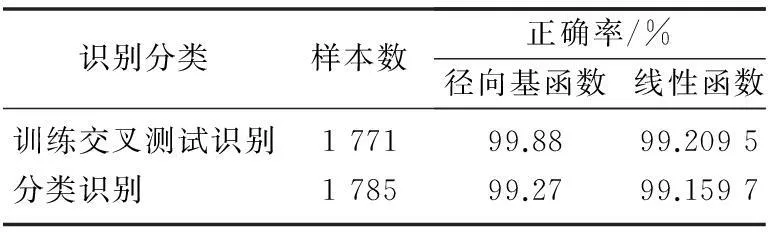
表3　大样本故障识别正确率

4结束语

试验结果表明，滚动轴承的振动信号经过三层小波包变换，将提取的八个频带的能量熵作为特征向量，能够较好地反映滚动轴承的六种运行状态；用分类性能优越的支持向量机(SVM)进行运行状态识别，准确率能达到99%以上；在线性函数、多项式函数、径向基函数这三种核函数比较中，多项式函数准确率最高。

参考文献

[1] 袁浩东,陈宏,侯亚丁,等.基于优化支持向量机的轴承故障诊断方法研究[J].机械设计与制造,2012(5):118-120.

[2] 王冬云,张文志,张建刚.小波包能量谱在滚动轴承故障诊断中的应用[J].轴承,2010(11):32-36.

[3] 王冬云,张文志.基于小波包变换的滚动轴承故障诊断[J].中国机械工程,2012(3):295-298.

[4] 邓乃扬.支持向量机:理论.算法与拓展[M].北京：科学出版社, 2009.

[5] Loparo K A.Bearings vibration data set[DB/OL].[2014-01-12].Case Western Reserve University.http://www.eecs.cwru.edu/laboratory/bearing/download.htm.

[6] 明安波,褚福磊,张炜.滚动轴承复合故障特征分离的小波-频谱自相关方法[J].机械工程学报,2013(3):80-87.

[7] 杨学存.基于小波频谱分析的滚动轴承故障诊断研究[J].煤矿机械,2013(1):289-291.

[8] 李永龙,邵忍平,曹精明.基于小波包与支持向量机结合的齿轮故障分类研究[J].西北工业大学学报,2010(4):530-535.------------------------------------------------------------------------------------------------

中图分类号：TH17

文献标志码：A

DOI:10.16086/j.cnki.issn1000-0380.201502004

国家自然科学青年基金资助项目(编号：11201426)。

修改稿收到日期：2014-08-12。

第一作者孙小权(1970-)，男，2005年毕业于复旦大学软件工程专业，获硕士学位，高级工程师；主要从事智能故障诊断、机械工程及自动化装备设计的研究。