钢轨平直度测量仪测试平台仿形面波形数据建模分析
2015-03-08沈正强上海铁路局科研所
沈正强 潘 超 上海铁路局科研所
钢轨平直度测量仪测试平台仿形面波形数据建模分析
沈正强 潘 超 上海铁路局科研所
目前钢轨平直度测量仪检测精度评定方法存在大量测量仪的检测数据未参与其检测精度评定的数据统计分析中,为了能精确评定测量仪检测精度,需更多千分尺测量数据而增加人工测量的工作量。采用BP神经网络基于千分尺测量得到仿形面曲线函数B0(n)建立仿形面波形数据数学模型,并基于BP模型残差分析引入周期性函数进行组合修正,以得到千分尺在各个对应的测量仪检测位置上的测量值的曲线函数B(n),通过对比分析测量仪的连续检测数据A(n)与B(n)的相似度,可更充分的对钢轨平直度测量仪的检测精度进行评定及其性能的全面验证。实验结果表明:组合模型建模方法正确可行、建模精度较高,其平均绝对误差仅为0.0218 mm,平均相对误差仅为1.09%。
千分尺;测量仪;建模;神经网络;组合模型
1 引言
钢轨平直度测量仪测试平台是评定GPC10-I型钢轨平直度测量仪的测量精度及对钢轨平直度测量仪的数学模型和数据处理的正确性进行全面验证的重要工具。测试平台仿形块采用铝合金材料加工,由于金属材料易存在形变,因此原有加工精度无法正确描述仿形面真实波形,需通过对仿形块仿形面的实际测量以得到仿形面的真实波形。目前采取的测量方法是人工使用千分尺以5 cm(或2.5 cm)的固定间距离散测量一定数量的特定位置形面的波形数据,以此得出一条以大理石水平尺为理想横坐标的波形曲线B0(n)作为仿形面的真实波形,而钢轨平直度测量仪以5 mm的间距连续测量得到仿形面检测数据A(n),并基于最小二乘插值计算得到测量仪在各个对应千分尺的测量位置上的检测值的曲线函数A(n)',通过对比分析A(n)'与B0(n)之间波形的相似度,以评定测量仪的检测精度,这不免使大量测量仪的检测值未参与其检测精度评定的后续数据统计分析中,同时为了能精确评定测量仪检测精度,必然需要更多千分尺测量数据,不免又增加人工测量的工作量。
神经网络的非线性映射逼近和学习能力,并行信息处理和容错能力,使其在工业系统中、尤其在复杂的非线性对象建模方面得到广泛应用。基于此,针对上述问题,本文采用BP神经网络基于B0(n)建立仿形面波形数据数学模型,并基于BP模型残差分析引入周期性函数进行组合修正,以保证该组合模型具有较高的建模精度。基于组合模型得到千分尺在各个对应的测量仪检测位置上的测量值的曲线函数B(n),通过对比分析测量仪的检测数据A(n)与B(n)的相似度,可更充分的对钢轨平直度测量仪的检测精度进行评定及其性能的全面验证。
2 仿形面波形数据数学建模
2.1 建模原理

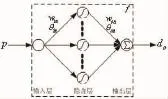
图1 神经网络结构
经过上述神经网络的自学习建模,可很好的反映出仿形面特定位置p与其对应特定位置处波形数值d之间复杂映射关系,但拟合出的BP趋势曲线通常是光滑的,不能满足隐含波动特征的数列,一般剔除趋势成分后的残差序列呈现一定程度的正负交替波动特征,具有不太规律的周期性,这说明原始波形序列隐含一定的周期成分和随机成分,并考虑到测试平台仿形面波形模拟的是线路钢轨顶面不平顺波形的情况,为了提高模型的建模精度,本文基于BP模型的残差序列对其所建模型进行修正。

考虑残差序列隐含周期成分,基于残差序列q(i),利用谐波分析构造周期波形模型如下
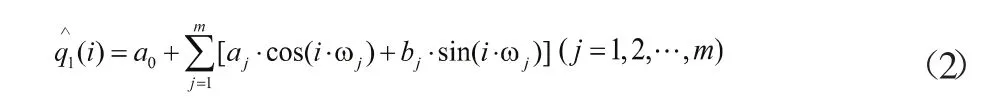
式(2)中:
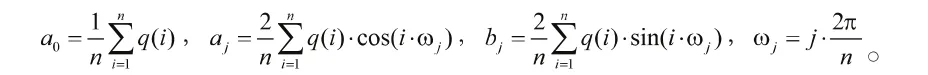
考虑残差序列隐含随机成分,基于残差序列q(i)波形的平均特征构造正弦残差修正周期函数模型如下



基于上述分析可得基于BP神经网络模型残差序列修正的组合模型为

2.2 建模结果
基于组合模型方法对钢轨平直度测量仪测试平台仿形面波形数据进行数学建模,所选钢轨平直度测量仪测试平台仿形面波形数据来源于2014年上海铁路局科技成果验收资料《GPC10-I型钢轨平直度测量仪及其测试平台》附录-仿形面到大理石水平尺的高度数据。

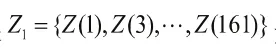
采用MATLAB7.0编写BP神经网络建模程序,其中隐含层神经元个数选取为20,隐含层激励函数采用正切S函数(tansig),输出层函数采用线性函数(purelin),目标误差eg= 0.0001,最大训练步数epoch=50000,采用带动量梯度下降改进型训练函数(traingdm),其学习速率lr=0.20,动量因子mc= 0.70,BP神经网络基于数据集Z1进行学习以完成建模。
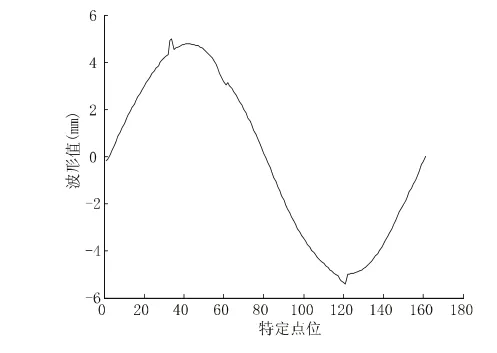
图2 仿形面波形
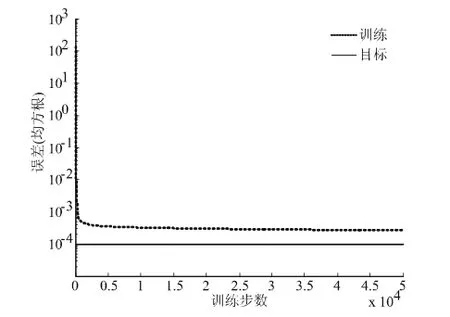
图3 BP神经网络训练误差
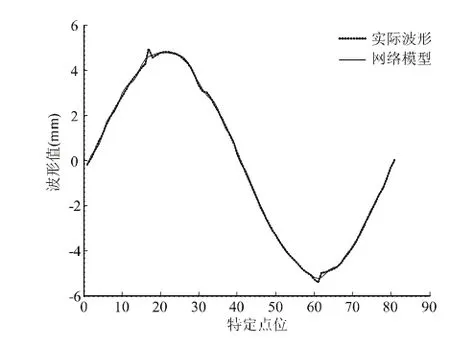
图4 仿形面波形BP网络建模结果

图5 仿形面波形BP网络建模误差
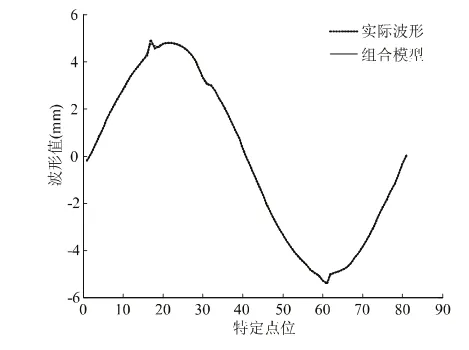
图6 仿形面波形组合模型建模结果

图7 仿形面波形组合模型建模误差
图3为其训练误差变化曲线,经过50000步的训练其均方根误差达到0.00027,图4、5分别为仿形面波形BP网络模型建模结果和建模误差图,图中看出BP网络模型建模效果较好,但仍存在较大的建模误差,且其建模残差序列呈现不太规律的周期性,显示原始波形序列隐含一定的周期成分和随机成分。
为了进一步提高模型的建模精度,基于BP模型残差分析引入周期性函数进行组合修正,其中组合修正模型参数分别为α=0.8、β=0.2及m=30,组合模型建模结果如图6、7所示,图中看出组合模型的建模精度优于单一BP模型建模精度,且很好的补偿了原始波形序列隐含的周期成分和随机成分,其建模误差基本均分布在±0.05 mm范围内。
3 组合模型的验证与分析
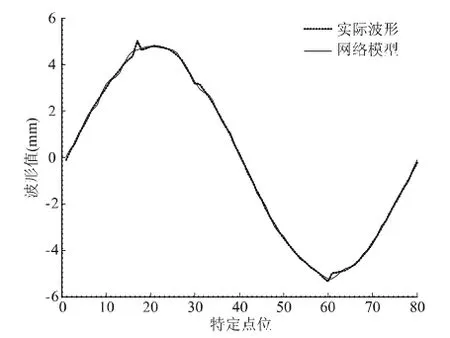
图8 仿形面波形BP网络测试结果

图9仿形面波形BP网络测试误差
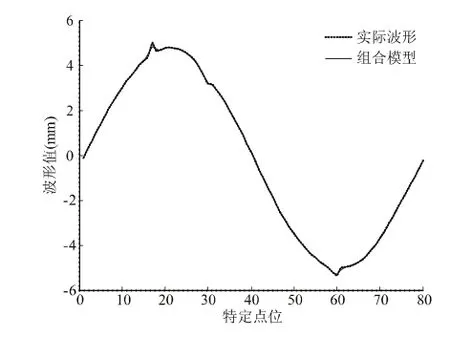
图10 仿形面波形组合模型测试结果

图11 仿形面波形组合模型测试误差
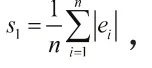
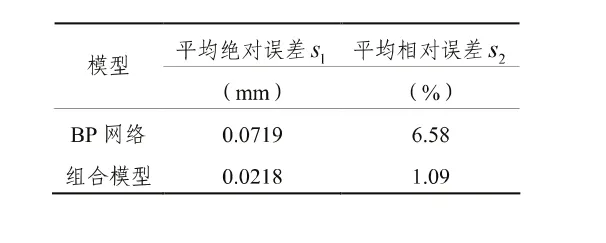
表1 两种模型性能指标
4 结论
(1)提出了一种组合模型建模方法,该方法仅需千分尺以10 cm的固定间距测量得到仿形面曲线函数B0(n)便可得到千分尺在各个对应的测量仪检测位置上的测量值的曲线函数B(n),解决了目前钢轨平直度测量仪检测精度评定方法存在的问题。
(2)实验结果表明:本文组合模型建模方法正确可行、建模精度较高,其平均绝对误差仅为0.0218 mm,平均相对误差仅为1.09%,基于此方法可更充分的对钢轨平直度测量仪的检测精度进行评定及其性能的全面验证。
[1]徐伟人,潘超.GPC10-I型钢轨平直度测量仪及其测试平台[R].上海:上海铁路局科学技术研究所,2014.
[2]陈增强,袁著祉.神经网络建模在热膨胀螺栓形变测量中的应用[J].控制与决策,2001,16(1):117-119.
[3]彭熙伟,杨会菊.液压泵效率特性建模的神经网络方法[J].机械工程学报,2009,45(8):106-111.
[4]何伟铭,宋小奇,甘屹等.传感器校正的优化灰色神经网络建模方法研究[J].仪器仪表学报,2014,35(3):504-512.
[5]李太福,侯杰,姚立忠等.Gamma Test噪声估计的Kalman神经网络在动态工业过程建模中的应用[J].机械工程学报,2014,50(18):29-35.
责任编辑:宋飞 龚佩毅
来稿时间:2015-5-18
