基于地震数据子集的波形反演思路、方法与应用
2015-03-08董良国黄超迟本鑫刘玉柱
董良国, 黄超, 迟本鑫, 刘玉柱
同济大学海洋地质国家重点实验室, 上海 200092
基于地震数据子集的波形反演思路、方法与应用
董良国, 黄超, 迟本鑫, 刘玉柱
同济大学海洋地质国家重点实验室, 上海 200092
地震数据与地下介质物性参数之间的复杂关系,决定了地震全波形反演在理论方法上面临着强烈的非线性难题.地下不同物性参数的不同分量在地震数据上具有不同的表现,勘探的不同阶段对地下介质模型的精度也具有不同的要求,这就决定了在地震全波形反演过程中不必时刻追求地震数据全部信息的匹配,部分信息的匹配就有可能解决现阶段的某些问题,还可以一定程度上规避匹配全部地震信息所遇到的强烈非线性难题.基于这样的考虑,我们提出了利用地震数据子集进行波形反演的思路,给出了统一的反演方法,并通过基于包络数据子集以及反射波数据子集的波形反演的理论模型与实际资料反演试验,证明了所提出的波形反演思路和方法的正确性.
全波形反演; 波形反演; 地震数据子集; 非线性; 目标函数; 核函数
1 引言
全波形反演(FWI)是通过使模拟数据和观测数据的信息达到最佳匹配来推测地下介质物性参数的(Tarantola,1984).从理论上讲,FWI可以考虑介质的诸多属性、考虑各种波的传播现象、利用各种地震信息,在理论上是目前利用地震数据解决地下介质性质最彻底的方法.在近10年期间,由于计算能力的提升、实际观测数据质量的提高,尤其是逆时偏移技术的发展和成功应用,推动了FWI的迅猛发展,掀起了FWI理论方法和实际应用研究的热潮.
然而,可以综合利用各种地震信息的FWI在理论方法上还面临着强烈的非线性难题(Virieux and Operto, 2009),其根本原因在于地震波传播的复杂性,即地震数据与地下介质物性参数之间的复杂变化关系(Jannane et al.,1989;董良国等,2013).另外,目前FWI在实际应用中也面临着诸多实际问题,如观测孔径不够宽、缺乏低频信息、震源子波难以确定、初始模型精度不高、复杂介质中地震波传播的准确描述困难、信噪比较低,等等.由于上述问题的复杂性以及诸多客观条件的限制,决定了FWI目前在实际中应用并不普遍,在地震学领域FWI还没有替代传统的走时层析和有限频层析技术,在地震勘探领域FWI也没有替代传统的地震数据处理和解释流程.
面对目前复杂的地震勘探问题,在传统的地震数据处理与解释中,将地下模型变化的高低波数分量分步解决的流程是很有道理的,这也是将一个复杂问题分步解决的基本思路和策略.面对理论上的困难以及实际地震资料的复杂性,再考虑到目前地震勘探要解决的实际问题,目前正在发展的FWI技术也应该放低身段,面向实际.也就是说,在全波形反演中没有必要时刻追求全部地震信息的匹配,因为匹配部分信息就有可能解决目前地震成像中的宏观速度模型建立问题,还可以一定程度上规避匹配全部地震信息极易遇到的强烈非线性难题.当然,匹配部分信息在理论上肯定会降低反演的分辨率,但不切实际的“过高的”模型分辨率并不利于地震成像质量的提高.
基于上述考虑,我们提出利用地震数据子集进行波形反演的思路与方法.下面,我们给出利用地震数据子集进行波形反演的基本思路,并给出基于不同地震数据子集的FWI统一的梯度计算公式.最后通过几种不同的地震数据子集进行理论模型与实际数据的波形反演试验,以证明基于不同地震数据子集的波形反演思路和方法的正确性.
2 基本思路与方法
2.1 基本思路
常规FWI是通过使模拟数据和观测数据的信息达到最佳匹配来推断地下介质参数的.设xs、xr和x分别为炮点、检波点和空间任意点的空间位置,时间域FWI最常用的最小平方目标函数为
J(m) =h1(u(m),d,m)
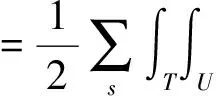
-d(xr,t;xs)]2dtd3x,
(1)
其中,h1是在参数为m时衡量全部模拟数据u和观测数据d之间匹配程度的函数.T为观测的最大时间,U为物理量u所在的空间(由于本文在时间域定义目标函数和计算地震波场,这时U为实数空间).物理参数m(x)∈M,其中M为模型参数空间,一般为实空间.显然,h1是从空间U×M到实数空间R的映射,J是从模型空间M到实数空间R的映射.
与此相对应的描述地震数据摄动与模型参数摄动之间的关系为
Δd=KΔm,
(2)
其中,Δd、K、Δm分别为数据残差、描述数据与模型参数之间关系的Fréchet导数或核函数、以及模型参数修改量.
在数据与模型参数之间的关系比较简单的情况下,像(2)式这样将地震数据和地下模型参数均看作一个整体的做法还是可行的.然而,地下模型具有性质不同的多个分量(DifferentComponents),例如高、低波数分量,而实际观测地震数据中也有性质不同的多个成分(DifferentContents)或数据子集(DifferentSubsets),例如折射波、反射波、面波等不同震相,走时、振幅、相位等不同信息,等等.这些不同数据子集与模型参数不同成分之间的非线性程度是不同的(董良国等,2013):模型的不同成分在不同震相上的体现不同,即使在同一震相上所体现出的信息也不同,例如速度低波数摄动主要体现在反射波走时上,而速度高波数摄动主要体现在反射波振幅上;初至波主要受浅中层结构的影响,而浅、中、深层介质性质都会影响来自深层的反射波.不同数据子集与不同模型参数成分之间的这种复杂关系,决定了不同数据子集具有不同的反演能力,这就要求我们对它们之间的关系进行具体分析,从而降低FWI的非线性程度.具体地说,就是将传统FWI中描述地震数据摄动与模型参数摄动之间的关系修改为
(3)
其中,Δdi、Δmj、Kij分别为数据子集残差、模型参数分量的修改量、以及描述不同数据子集与不同模型参数成分之间关系的子核函数(Sub-Kernels).
通过上述关系发现,不同成分的模型参数修改量主要是由子核函数和数据子集残差决定的.目前模型参数修改量的求取主要有两种方法:伴随状态法(Tarantola, 1984;Trompetal., 2005;Plessix2006)将数据残差沿核函数(波路径)反投影,散射积分法(Zhao, 2005;Chenetal., 2007;Liuetal., 2015)则显式计算和存储核函数并求解反演(层析)方程组.而我们这里提出的基于数据子集的波形反演思路,就是根据勘探的不同阶段对地下介质模型精度要求的不同,通过分析地震数据子集和相应的子核函数的性质,以便在反演中将适当的地震数据子集残差沿着合理的子核函数进行反投影,从而决定模型参数的哪种波数成分在空间何处进行更新.
核函数的计算方法和特征分析是有限频层析(Dahlenetal., 2000;Trompetal., 2005;Liuetal., 2009)、波动方程层析(Woodward, 1992)和全波形反演(Tarantola, 1984;Prattetal., 1998;VirieuxandOperto, 2009)中的核心问题(实际上,三者本质上一致的).不同地震数据子集所包含的信息差别很大,体现不同地震数据子集与模型参数不同成分之间关系的子核函数也具有显著差异,对于不同的地震信息在反演中当然采用不同的子核函数,进而可以对模型中的高低波数成分进行解耦(Chietal., 2015).折射波对中浅层模型的背景速度较为敏感,将折射波的数据子集残差沿折射波核函数反投影,可以较好地更新折射波波路径覆盖区域的背景速度.反射波的波形信息(Xuetal., 2012)或走时信息(Chietal., 2015)可以用来反演中深层的背景速度,前提是将反射波数据子集的残差沿反射波子核函数(Rabbit-ear)进行反投影.否则,反射波通常只能更新模型深部的高波数成分.
在对核函数进行分解以及对不同子核函数的物理含义进行具体分析的基础上,我们就可以利用部分地震信息进行波形反演,以降低常规FWI中匹配全部信息所引起的高度非线性问题.因为匹配整个地震道的标准实在太高,在初始模型还达不到要求情况下,匹配整个地震道所有信息的难度实在太大,有时也没有必要(因为我们经常要解决的仅仅是宏观速度模型),能把地震道的某个主要特征匹配好也许就可以达到某些要求了(如构造成像).也就是说,要抛弃粗放式的对整个地震记录的匹配方式,而是要仔细分析不同参数变化在不同地震数据子集上的具体体现,在精细分析观测地震数据具体特点的基础上,在FWI的不同阶段采用不同的地震数据子集.
2.2 基于地震数据子集的波形反演方法
在上述思路指导下,下面我们给出基于地震数据子集的波形反演的具体方法.
为简单起见,这里只是考虑最小平方目标函数.为此,我们把基于地震数据子集波形反演的最小平方目标函数定义为
J(m) =h(u(m),d,m)
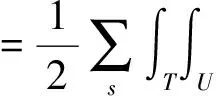
-R(d(xr,t;xs))]2dtd3x,
(4)
其中,R(u)和R(d)分别表示对数据u和d进行某种数学操作,R就是为提取某个地震数据子集的操作算子.需要说明的是,算子R是一个抽象的形式,在实际反演中,在不同的反演阶段、根据不同的反演目标,R要采用不同的具体形式.显然,h是衡量模拟数据子集R(u(xr,t,m;xs))和观测数据子集R(d(xr,t;xs))之间匹配程度的函数.
设地震波场u(x,t,m;xs)所满足的波动方程为
F(u(m),m)=0.
(5)

使(4)式的目标函数最小化的求解过程通常采用局部优化方法,其模型更新公式为
mk+1=mk+αkpk,
(6)
由(4)式可得


(7)

(8)
其中,计算伴随场λ=λ(x,t,m;xs)的伴随方程为


(9)
其中,星号*表示共轭,方程的右端项为伴随震源.

可见,利用不同的地震数据子集进行波形反演时,梯度计算具有统一的形式,即(8)和(9)式,而且形式与常规FWI完全一致,伴随方程(9)的形式也相同.只是面对不同的正问题、不同的目标函数形式、以及不同的地震数据子集,计算伴随场的伴随震源不同而已.对于如(4)式的最小平方目标函数,其伴随震源不但取决于接收点处模拟数据和观测数据的子集R(u(xr,t,m;xs))和R(d(xr,t;xs))之差,还与选取数据子集的方式(即算子R)有关.
至于选取什么样的地震数据子集,取决于实际地震数据特征和不同反演阶段.通过利用具体的体现数据子集和不同模型参数分量之间关系的子核函数来确定反演的梯度,就可以实现分步骤、分尺度的地震波形反演.
3 基于地震数据子集的波形反演应用举例
从理论上讲,只要能够从地震数据中抽取具有一定意义的信息,均可以利用这些信息构成的地震数据子集按照上述思路进行波形反演.体现地震数据某个特征的地震数据子集,它需要具备以下条件:(1)能够体现地震数据的某个或某些变化特点;(2)在物理上和(或)从信号角度具有一定的含义;(3)可以通过一定的数学手段进行提取.
实际上,以前的一些学者提出的一些FWI反演方法和策略,也是不同程度地体现了基于地震数据子集进行波形反演的基本想法,这些方法和策略的目的都是通过利用部分信息来降低波形反演的非线性程度.这些数据子集可以是:
(1) 地震数据中某种特定震相构成的数据子集.例如,若算子R是选取初至波的波形,相应的反演则退化为初至波波形反演(Shenget.al.,2006)、高斯束初至波波形反演(刘玉柱等,2014);若算子R是选取反射波的波形,相应的反演则退化为反射波全波形反演(Xuetal., 2012).
(2) 地震数据中特定时间或特定空间观测孔径的信息构成的数据子集.例如,为了降低反演的非线性程度,算子R可以是选取地震记录某一个时窗波形的操作,这时相应的反演就退化为层剥离全波形反演(Wangetal., 2009;Yangetal.,2013);若算子R是选取不同偏移距的地震数据,相应的反演就是采用分偏移距反演策略的全波形反演(Singh,1989;董良国等,2013).
(3) 地震数据经过特定数学变换后构成的数据子集.例如,若算子R是Laplace变换算子,这时上述基于数据子集的FWI就退化为Laplace域全波形反演(ShinandCha, 2008),实际上就是通过Laplace变换算子、主要利用初至波的走时信息,更稳健地为下一步的反演提供一个低波数初始速度模型.若算子R是对地震道进行积分的算子,这时相应的反演就退化为基于道积分的全波形反演(Liuetal.,2011;Donnoetal.,2013),这种方法可以在数据缺失低频或者初始模型不好时为常规FWI提供一个较好的初始模型.若算子R是通过Hilbert变换提取地震道的包络,相应的反演就变为基于包络的全波形反演(Chietal.,2013,2014;Wuetal.,2014;Huangetal.,2015),在地震数据缺失低频信息时,可以利用这种波形反演方法建立一个相对可靠的初始速度模型.如果算子R是把观测数据和模拟数据之间的褶积运算以及通过Hilbert变换提取地震道包络的运算综合在一起的一种操作,这时上述基于数据子集的FWI就退化为不依赖子波、基于包络的全波形反演方法(敖瑞德等,2015),在数据缺失低频信息、子波未知、先验模型信息缺乏时,这种FWI方法可以提供一个较好的初始速度模型.而司空见惯的多尺度分频反演策略(Bunksetal.,1995;SirgueandPratt,2004;刘国峰等,2012),实际上也是利用低频地震数据子集构造的目标函数非线性程度低的特点,来更稳健地建立一个相对可靠的低波数初始速度模型,以此为基础再逐步利用高频成分的地震数据子集,从而在反演中逐渐提高反演的分辨率.
另外,地震数据中某种特定信息也可以构成特定的地震数据子集,利用这样的地震数据子集当然也可以进行反演.例如,若算子R是利用相关确定初至波的走时,相应的反演则退化为初至波波动方程走时反演(LuoandSchuster,1991);若算子R是利用相关确定反射波的走时,相应的反演则退化为反射波波形反演(Chietal.,2015).可以预测,若算子R是选取反射波振幅的某种操作,相应的反演则退化为类似AVO技术的反射波振幅反演.基于这样的地震波振幅等特定信息进行反演的梯度计算方法能否用(8)式和(9)式统一表达,目前我们还不能确定,需要作进一步的分析.
至于选取何种地震数据子集,取决于反演所处的阶段和反演目的,还取决于实际地震资料的特点.如果是为了反演浅层模型,FWI过程中可以只选取初至波数据子集;如果是利用FWI为偏移成像提供宏观速度模型,可以选取体现地震数据宏观信息的数据子集,例如走时信息、地震道包络、Laplace变换、积分变换、相位信息等;如果成像问题已经解决,需要利用FWI进行精细储层反演与描述,就需要考虑利用体现数据精细变化特征的地震数据子集,因为储层的变化主要体现在地震数据的细微变化特征上.
我们提出的波形反演是一种概括性的思路,具体可以表现为许多种不同的波形反演方法.根据所采用的地震数据子集的不同,其中的一些方法可以反演模型的长波长分量,而另一些方法可以在初始模型较好情况下反演模型的精细结构.
如果是想通过FWI为成像提供一个具有更高精度的宏观速度模型,在全波形反演中只需要匹配部分信息就有可能解决这样的建模问题,同时可以降低反演的非线性程度.由于要反演的是速度变化的低波数成分,FWI中所选择的部分信息主要应该体现地震数据的宏观变化特征.因此,下面我们通过体现地震数据宏观特征的三个数据子集的例子,来说明基于地震数据子集的波形反演的思路与方法的有效性.至于不同数据子集反演时具体的梯度公式,均可以利用梯度的通式(8)和(9)得到,本文不再赘述.
需要说明的是,以下三种方法主要是利用了地震数据的宏观特性,这些方法的反演结果当然也就体现了模型的大尺度变化特征.从这个意义上说,下面所列举的三个基于地震数据子集的波形反演方法,可以划归为速度建模方法的范畴,从三个方法的反演结果上也可以得出这样的结论.但是,与目前通用的建模方法相比(Al-Yahya, 1989;MacKayandAbma, 1992;SymesandCarazzone,1991;LiuandBleistein,1995;SavaandFomel, 2003),本文列举的三个方法不需要人工干预,自动化程度更高.
3.1 基于包络地震数据子集的波形反演应用举例
在实际地震资料波形反演中,低频成分缺失与初始模型较差是目前高度非线性FWI面临的两个实际难题(二者均会引起Cycle-skipping现象),同时,这两个问题又是紧密联系在一起的:地震数据中低频成分缺失越严重,FWI就需要更高精度的初始模型.也就是说,如果能够通过其他途径建立一个高精度的初始模型,即使地震数据中缺失一定的低频成分,FWI也可能得到一个较好的反演结果.包络信息主要反映了地震道的宏观特征,可以通过Hilbert变换提取地震道包络来构造目标函数,从而反演速度模型的低波数成分.包络是地震数据子集之一,当然可以利用(8)和(9)式计算基于包络地震数据子集的波形反演的梯度.
图1和图2是Marmousi模型试验结果.由于地震数据中滤掉了5 Hz以下的频率成分,沿深度呈梯度变化的速度初始模型(图1a)精度又不高,常规FWI的反演结果比较差(图1b),反演中局部极值问题严重.而利用同样的梯度初始模型,基于地震道包络的波形反演结果(图2a)在反映模型的宏观变化趋势方面明显优于图1b,较好地反映了实际模型的低波数成分.以图2a作为初始模型再进行常规的全波形反演,即使在地震数据缺失低频成分、初始模型也很差的情况下,反演结果也非常理想(图2b),反演结果的高低波数成分都比较好.

图1 梯度初始模型(a)以及传统FWI反演结果(b)Fig.1 (a) The initial gradient model and (b) the inverted results of traditional FWI
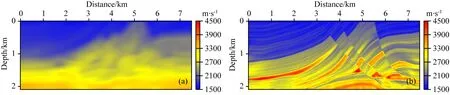
图2 利用图1a的梯度初始模型、基于包络数据子集的FWI反演结果(a),以及利用图2a作为初始模型的传统FWI反演结果(b)Fig.2 (a) The inverted results by FWI of envelope data subset-based using the gradient initial model of Fig.1a, and (b) the inverted results of traditional FWI using the initial model of Fig.2a

图3 初始速度模型(a)及RTM结果(a)Fig.3 (a) The initial velocity model and (b) the RTM imaging result

图4 基于包络FWI反演的速度(a)及RTM结果(b)Fig.4 (a) The inverted velocity model by FWI of envelope data subset-based and (b) the RTM imaging result
图3是南海某二维测线的初始层速度模型以及逆时偏移结果,图4是利用地震道包络数据子集的FWI反演结果及相应的RTM偏移结果.可以看出,通过包络FWI反演的模型分辨率大幅度提高,呈现出比较精细的速度横向变化(图4a),成像质量显著改善(图4b).
3.2 低频缺失时基于弹性波包络数据子集的波形反演应用举例
包络信息主要反映了地震道的宏观特征,可以利用包络来反演速度模型的低波数成分.利用声波方程、基于单分量地震数据的包络进行纵波速度的单参数反演,最近取得了较好的效果(Chi et al., 2013,2014; Wu et al.,2014).
在利用多分量地震数据进行弹性波全波形反演(EFWI)过程中,同样存在低频成分缺失与初始模型较差的难题,对于波长较小的横波速度而言这个问题更加突出(Brossier et al., 2009;Baeten,2013).为此,我们利用弹性波多分量数据的包络这个多分量地震数据子集,来反演地下介质纵横波速度的长波长分量,为以后的地下参数的精细反演提供较好的纵横波速度初始模型.
图5是Marmousi2纵波速度的真实模型以及用于EFWI的初始模型.由于两个分量的地震数据中5Hz以下的频率成分被滤掉,且纵横波速度均采用沿深度呈常梯度变化的初始模型,所以,常规的EFWI反演结果出现严重的局部极值问题(图6).而利用多分量地震道包络信息的反演结果(图7)却较好地恢复了真实模型的长波长成分,以图7结果作为初始模型再进行常规的EFWI,纵横波速度均取得了比较好的反演结果(图8).可见,尽管多分量地震数据中低频缺失、初始模型精度也很差,但这种两步法的EFWI反演方法却得到了非常理想的反演结果.
从X=7.5 km处反演的纵横波速度剖面上也可以看到(见图9),利用基于弹性波包络数据子集的EFWI结果作为初始模型的常规EFWI反演结果(图9中红线),在2.2 km深度以上几乎与真实纵横波速度(图9中黑线)完全一致,而常规EFWI反演结果(图9中蓝线)与真实纵横波速度差距很大,横波速度尤其明显,反演过程明显陷入了局部极值.可见,在多分量地震数据中缺失低频信息以及初始模型不好情况下,利用弹性波包络这样的数据子集,可以来反演地下介质纵横波速度的长波长分量,从而为下一步的精细反演提供较好的纵横波速度初始模型.
3.3 基于反射波地震数据子集的波形反演应用举例
在实际地震资料全波形反演中,要反演中深层的速度结构,必须利用反射波数据.为了克服匹配全部地震信息的困难,可以通过波形的相关来确定模拟与观测的反射波的时差,然后利用各地震道时差定义反演的目标函数,这样可以有效地反演中深部的宏观速度变化.需要说明的是,这种基于反射波地震数据子集的波形反演方法(RFWI)与常规的偏移速度分析不同,本文是在数据域进行的,并且是一种不需人工干预的全自动速度反演方法.

图5 Marmousi-2纵波速度真实模型(a)及常梯度初始模型(b)Fig.5 2D Marmousi-2 true model (a) and linear gradient initial model (b) for P-wave velocity

图6 多分量地震数据中不含5 Hz以下频率成分时的常规EFWI反演结果:(a)纵波速度; (b)横波速度Fig.6 P-wave (a) and S-wave (b) velocity models obtained by conventional EFWI without low frequency below 5 Hz
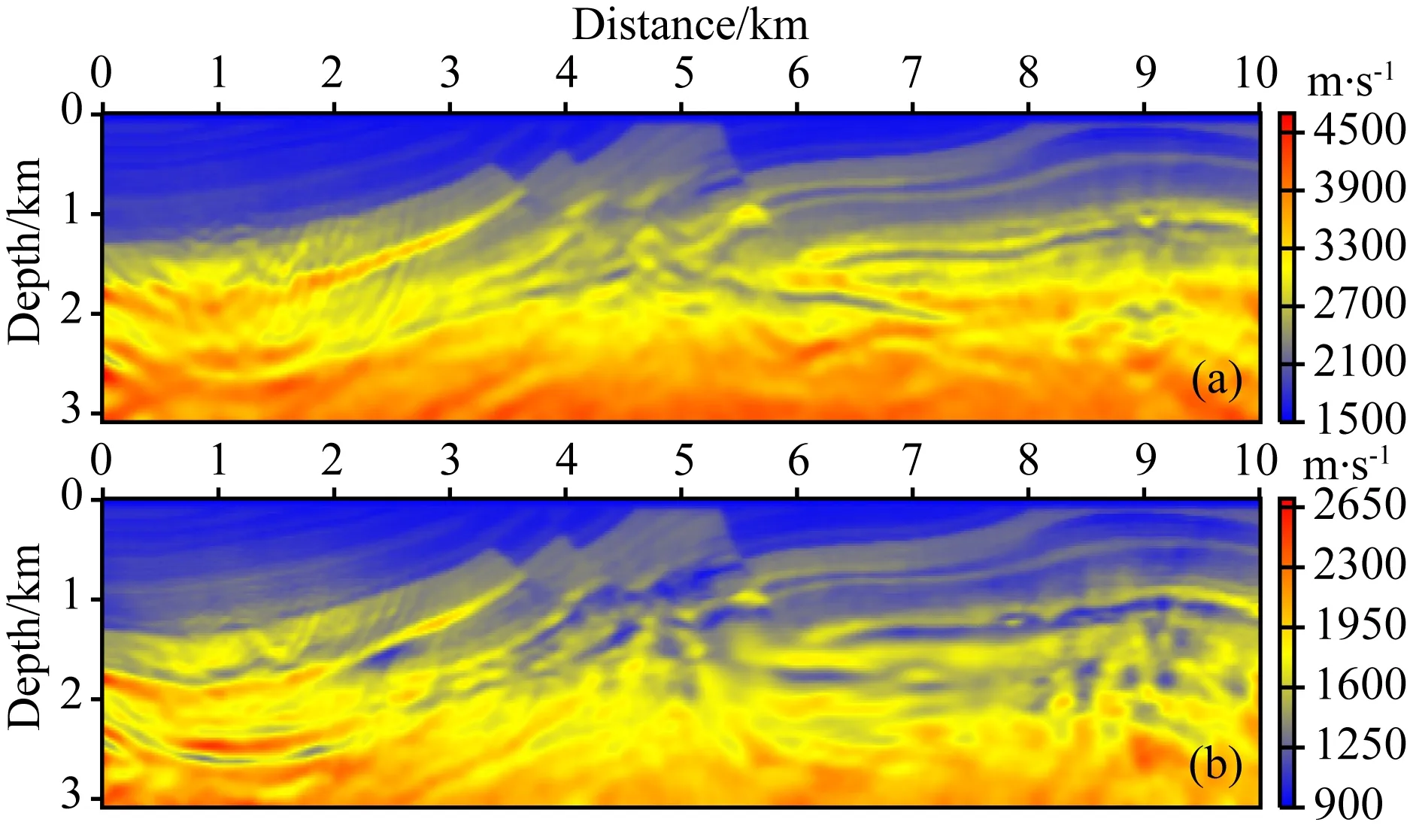
图7 多分量地震数据中不含5Hz以下频率成分时,基于弹性波包络数据子集的EFWI反演结果:(a) 纵波速度;(b) 横波速度Fig.7 P-wave (a) and S-wave (b) velocity models obtained by FWI of elastic envelope data subset-based without low frequency below 5 Hz
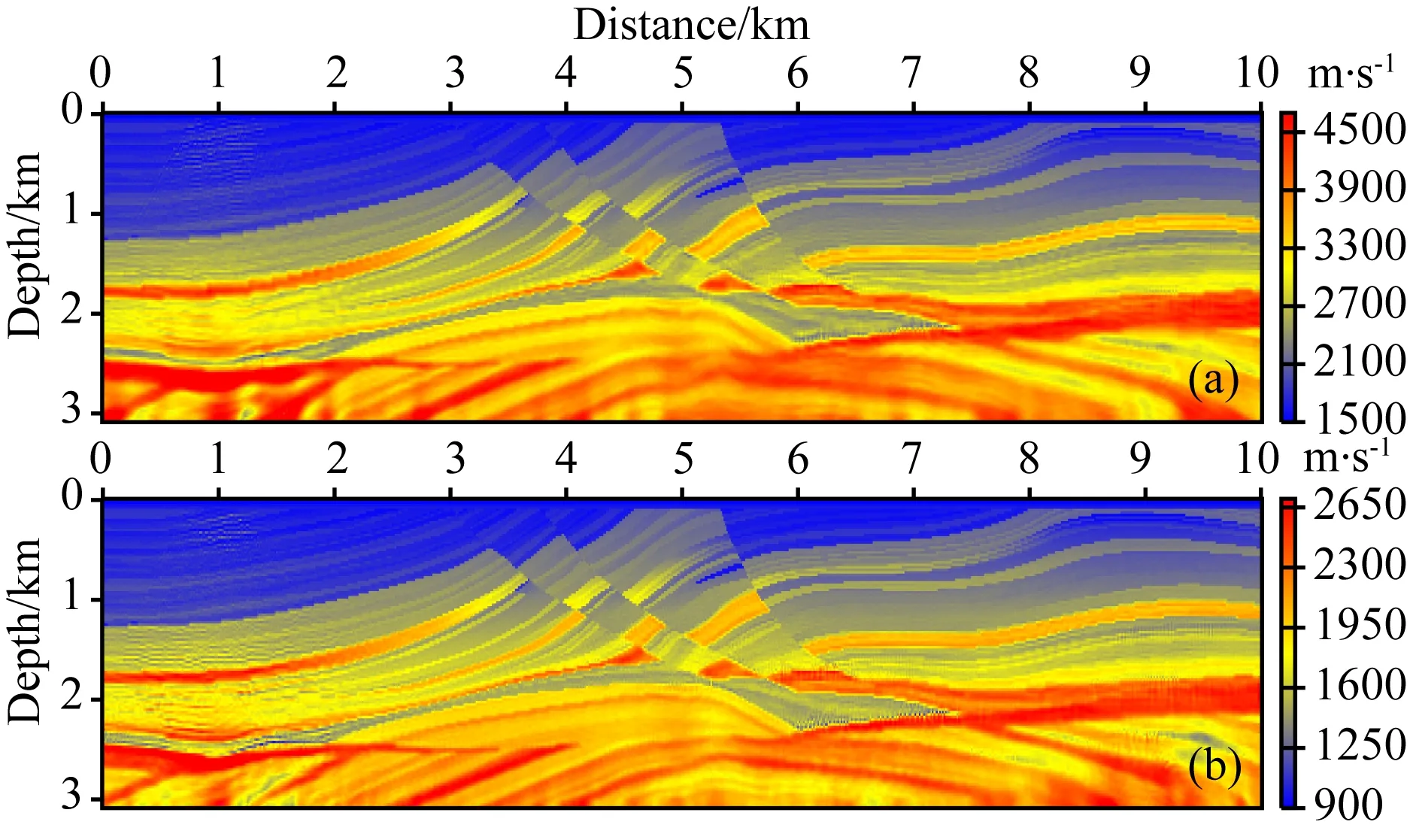
图8 多分量地震数据中不含5Hz以下频率成分时,以图7作为初始模型的常规EFWI反演结果:(a) 纵波速度;(b) 横波速度Fig.8 P-wave (a) and S-wave (b) velocity models obtained by conventional EFWI using Fig.7 as the initial models without low frequency below 5 Hz

图9 不同方法反演的纵横波速度剖面对比(X=7.5 km处). 真实模型(黑实线)、常梯度初始模型(黑虚线)、常规EFWI反演结果(蓝线)、利用基于弹性波包络数据子集的EFWI反演结果作为初始模型的常规EFWI反演结果(红线)Fig.9 Comparison between velocity profiles extracted from models recovered by conventional EFWI (blue line) and our two-step EFWI method (red line) for Vp and Vs at the location of X=7.5 km. The starting vertical gradient model and the true model are depicted with black dashed and solid lines, respectively
反射波相关目标函数的构建、以及体现反射波与模型长波长分量之间关系的子核函数的确定,是这种FWI反演方法的两个关键.该方法的具体细节请见文献(Chi et al., 2015),不再赘述,这里只是想通过展示该方法在实际资料反演中的效果,来说明基于反射波地震数据子集的波形反演的有效性.
对中国东海一条二维拖缆地震数据,平滑后的叠前时间偏移速度分析结果见图10a,对应的高斯束叠前深度偏移结果见图11.以图10a作为初始模型,通过基于反射波地震数据子集进行波形反演,速度模型的更新量见图10b.利用基于反射波地震数据子集波形反演结果,得到的高斯束叠前深度偏移结果见图12.可以看到,成像质量较RFWI反演前的图11得到了大幅度提高,同相轴连续性显著改善,许多断层更加清晰,尤其是2 km深度处的上超以及削截等沉积现象在图12上更加清晰.在基于反射波地震数据子集波形反演后的角度域共成像点道集上(图13),同相轴基本拉平,说明了波形反演得到的速度模型较初始模型更加准确.
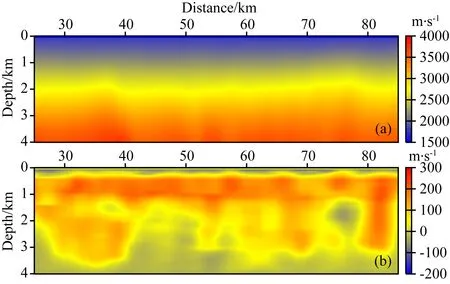
图10 基于反射波地震数据子集的波形反演初始模型(a)及反演前后的速度修改量(b)Fig.10 (a) The initial velocity model for FWI of reflection data subset-based, and (b) the difference between the RFWI result and the initial velocity model
4 讨论
根据实际观测地震数据的具体特点,在不同的反演阶段,选择不同的地震数据子集,有针对性地构造非线性程度更低的目标函数,以实现分步骤、分尺度的全波形反演,其中每个步骤的反演都可以称之为基于地震数据子集的波形反演方法.这是地震数据和地下参数之间复杂关系的客观要求,也是地震数据处理与解释中的不同阶段不同反演目标的客观要求.
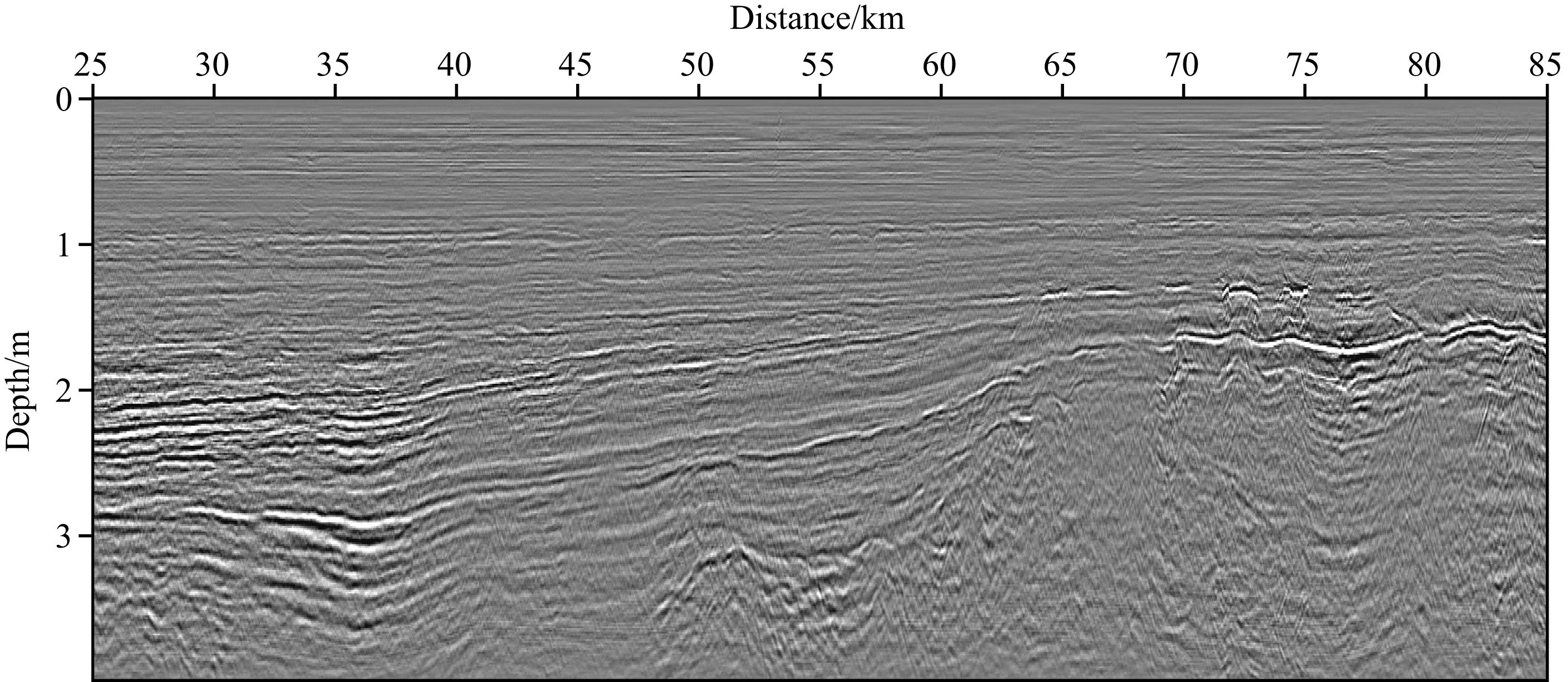
图11 基于初始模型的叠前深度偏移结果Fig.11 The pre-depth migration result using the initial velocity model

图12 以RFWI反演结果作为偏移速度模型的叠前深度偏移结果Fig.12 The pre-depth migration result using the RFWI result

图13 RFWI前(a)后(b)的角度域共成像点道集Fig.13 The common image gathers with (a) before and (b) after RFWI result
当然,有人会问:“这样做还是全波形反演吗?”.到底什么是FWI? 我们现在都承认,Tarantola(1984)和Lailly(1983)建立了FWI的理论框架,但他们当时都没有把他们的方法称作FWI,他们更多地使用数据拟合(data fitting)的概念,全波形反演(FWI)一词只是在1986年才出现(Pan and Phinney ,1986).在Tarantola以第一作者身份撰写的所有文章中,我们也难以明确见到FWI的影子,但这并不影响他在FWI发展中的开创性贡献.而Tarantola在地震反演中的主要贡献就是在数据拟合的框架下,搭起了参数反演和地震偏移成像之间的桥梁.
对地震记录全部信息的匹配是地震反演的最高理想,但在不同的反演阶段,面对诸多难题,明智而现实的作法是根据实际情况适当降低反演标准,不再刻意追求对地震记录全部信息的匹配,而是把对地震数据的部分信息进行匹配看作反演的阶段目标,这也就是基于地震数据子集的波形反演.
因此,将FWI人为定义为对地震记录全部信息的匹配,必然会极大限制FWI的发展.用对地震数据的部分信息进行匹配来反演介质参数的思路方法来定义FWI,这样会给FWI更大的空间,会更好地解决实际问题.
5 结论
(1) 面对FWI面临的强烈非线性问题以及实际资料中的诸多现实难题,本文提出了基于地震数据子集的波形反演思路,并给出了统一的反演方法.对不同的地震数据子集,梯度具有统一的计算形式,而且均可以通过地震波的正反向两次传播模拟进行计算.只是对不同的正问题、不同的地震数据子集以及不同形式的目标函数,反向传播的伴随震源不同而已.
(2) 所谓基于地震数据子集的波形反演,就是要抛弃FWI中对整个地震记录的匹配方式,而仔细研究不同参数在不同地震数据子集上的具体体现,在精细分析资料的基础上,在FWI的不同阶段采用不同的地震数据子集.并将该数据子集的残差沿着合理的子核函数进行反投影,从而决定模型中的哪种波数成分在空间何处进行更新.
(3) 即使在初始模型精度不高、地震数据低频缺失的情况下,利用地震道包络以及反射波地震数据子集,通过构建合理的目标函数,可以较好地反演地下速度模型的长波长分量.理论模型以及实际资料的波形反演及成像结果,充分证明了基于地震数据子集的波形反演思路与方法的正确性.
致谢 感谢同济大学程玖兵教授和王腾飞博士在高斯束叠前深度偏移方面提供的帮助.
Al Yahya K M. 1989. Velocity analysis by iterative profile migration.Geophysics, 54(6): 718-729. Ao R D, Dong L G, Chi B X. 2015. Source-independent envelope-based FWI to build an initial model.ChineseJ.Geophys. (in Chinese), 58(6): 1998-2010, doi: 10.6038/cjg20150615.
Baeten G, de Maag J W, Plessix R E, et al. 2013. The use of low frequencies in a full-waveform inversion and impedance inversion land seismic case study.GeophysicalProspecting, 61(4): 701-711.
Brossier R, Operto S, Virieux J. 2009. Seismic imaging of complex onshore structures by 2D elastic frequency-domain full-waveform inversion.Geophysics, 74(6): WCC105-WCC118.
Bunks C, Saleck F M, Zaleski S, et al. 1995. Multiscale seismic waveform inversion.Geophysics, 60(5): 1457-1473.
Chen P, Zhao L, Jordan T H. 2007. Full 3D tomography for the crustal structure of the Los Angeles region.BulletinoftheSeismologicalSocietyofAmerica, 97(4): 1094-1120, doi: 10.1785/0120060222.
Chi B X, Dong L G, Liu Y Z. 2013. Full waveform inversion based on envelope objective function. ∥75th Annual International Conference and Exhibition, EAGE, Extended Abstracts.
Chi B X, Dong L G, Liu Y Z. 2014. Full waveform inversion method using envelope objective function without low frequency data.JournalofAppliedGeophysics, 109: 36-46.
Chi B X, Dong L G, Liu Y Z. 2015. Correlation-based reflection full waveform inversion.Geophysics, 80(4): R189-R202, doi: 10.1190/GEO2014-0345.1.
Dahlen F A, Hung S H, Nolet G. 2000. Fréchet kernels for finite-frequency traveltimes—I. Theory.GeophysicalJournalInternational, 141(1):157-174, doi: 10.1046/j.1365-246X.2000.00070.x.Dong L G, Chi B X, Tao J X, et al. 2013. Objective function behavior in acoustic wave full-waveform inversion.ChineseJ.Geophys. (in Chinese), 56(10): 3445-3460, doi: 10.6038/cjg20131020.Donno D, Chauris H, Calandra H. 2013. Estimating the Background Velocity Model with the Normalized Integration Method. ∥ 75th Annual International Conference and Exhibition, EAGE, Extended Abstracts. Huang C, Dong L G, Chi B X, et al. 2015. Elastic envelope inversion using multicomponent seismic data with filtered-out low frequency.AppliedGeophysics,12(3):362-377.
Jannane M, Beydoun W B, Crase E, et al. 1989. Wavelengths of earth structures that can be resolved from seismic reflection data.Geophysics, 54(7): 906-910.
Lailly P. 1983. The seismic inverse problems as a sequence of before stack migration. ∥ Conference on Inverse Scattering Theory and Application, Society of Industrial and Applied Mathematics, Proceedings, 206-220.
Liu G F, Liu H, Meng X H, et al. 2012. Frequency-related factors analysis in frequency domain waveform inversion.ChineseJ.Geophys. (in Chinese), 55(4): 1345-1353, doi: 10.6038/j.issn.0001-5733.2012.04.030.
Liu J, Chauris H, Calandra H. 2011. The Normalized Integration Method—an alternative to Full Waveform Inversion?. ∥ 17th European Meeting of Environmental and Engineering Geophysics of the Near Surface Geoscience Division of EAGE, Leicester, UK.Liu Y Z, Dong L G, Wang Y W, et al. 2009. Sensitivity kernels for seismic Fresnel volume tomography.Geophysics, 74(5): U35-U46, doi: 10.1190/1.3169600.
Liu Y Z, Xie C, Yang J Z. 2014. Gaussian beam first-arrival waveform inversion based on Born wavepath.ChineseJ.Geophys. (in Chinese), 57(9): 2900-2909, doi: 10.6038/cjg20140915.
Liu Y Z, Yang J Z, Chi B X, et al. 2015. An improved scattering-integral approach for frequency-domain full waveform inversion.GeophysicalJournalInternational, 202(3): 1827-1842.
Liu Z Y, Bleistein N. 1995. Migration velocity analysis: Theory and an iterative algorithm.Geophysics, 60(1): 142-153.
Luo Y, Schuster G T. 1991. Wave-equation traveltime inversion.Geophysics, 56(5): 645-653.
MacKay S, Abma R. 1992. Imaging and velocity estimation with depth-focusing analysis.Geophysics, 57(12): 1608-1622.
Pan G S, Phinney R A. 1986. Full waveform inversion ofp-τseismogram. ∥ 56th Ann. Internat. Mtg. Soc. Expl. Geophys., Expanded Abstracts. http:∥dx.doi.org/10.1190/SEGEAB.5.Plessix R E. 2006. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications.Geophys.J.Int., 167(2): 495-503, doi: 10.1111/j.1365-246X.2006.02978.x.
Pratt R G, Shin C, Hick G. 1998. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion.GeophysicalJournalInternational, 133(2): 341-362, doi: 10.1046/j.1365-246X.1998.00498.x.
Sava P, Fomel S. 2003. Angle-domain common-image gathers by wavefield continuation methods.Geophysics, 68(3): 1065-1074.
Sheng J M, Leeds A, Buddensiek M, et al. 2006. Early arrival waveform tomography on near-surface refraction data.Geophysics, 71(4): U47-U57. Shin C, Cha Y H. 2008. Waveform inversion in the Laplace domain.Geophys.J.Int., 173(3): 922-931.
Singh S C, West G F, Bregman N D, et al. 1989. Full waveform inversion of reflection data.J.Geophys.Res., 94(B2): 1777-1794.
Sirgue L, Pratt R G. 2004. Efficient waveform inversion and imaging: A strategy for selecting temporal frequencies.Geophysics, 69(1): 231-248.
Symes W W, Carazzone J J. 1991. Velocity inversion by differential semblance optimization.Geophysics, 56(5): 654-663.
Tarantola A. 1984. Inversion of seismic reflection data in the acoustic approximation.Geophysics, 49(8): 1259-1266, doi: 10.1190/1.1441754.
Tromp J, Tape C, Liu Q Y. 2005. Seismic tomography, adjoint methods, time reversal and banana-doughnut kernels.GeophysicalJournalInternational, 160(1): 195-216, doi: 10.1111/j.1365-246X.2004.02453.x.Virieux J, Operto S. 2009. An overview of full-waveform inversion in exploration geophysics.Geophysics, 74(6):WCC1-WCC26, doi: 10.1190/1.3238367.
Wang Y H, Rao Y. 2009. Reflection seismic waveform tomography.J.Geophys.Res., 114(B3): B03304, doi:10.1029/2008JB005916.
Woodward M J. 1992. Wave-equation tomography.Geophysics, 57(1):15-26, doi: 10.1190/1.1443179.
Wu R S, Luo J R, Wu B Y. 2014. Seismic envelope inversion and modulation signal model.Geophysics, 79(3): WA13-WA24.
Xu S, Wang D, Chen F, et al. 2012. Full waveform inversion for reflected seismic data. ∥ 74th Annual International Conference and Exhibition, EAGE, Extended Abstracts. Yang J Z, Liu Y Z, Dong L G. 2013. Time-windowed frequency domain full waveform inversion using phase-encoded simultaneous sources. ∥ 75th Annual International Conference and Exhibition, EAGE, Extended Abstracts.Zhao L. 2005. Fréchet kernels for imaging regional earth structure based on three-dimensional reference models.BulletinoftheSeismologicalSocietyofAmerica, 95(6): 2066-2080, doi: 10.1785/0120050081.
附中文参考文献
敖瑞德, 董良国, 迟本鑫. 2015. 不依赖子波、基于包络的FWI初始模型建立方法研究. 地球物理学报, 58(6): 1998-2010, doi: 10.6038/cjg20150615.
董良国, 迟本鑫, 陶纪霞等. 2013. 声波全波形反演目标函数性态. 地球物理学报, 56(10): 3445-3460, doi: 10.6038/cjg20131020.
刘国峰, 刘洪, 孟小红等. 2012. 频率域波形反演中与频率相关的影响因素分析. 地球物理学报, 55(4): 1345-1353, doi: 10.6038/j.issn.0001-5733.2012.04.030.
刘玉柱, 谢春, 杨积忠. 2014. 基于Born波路径的高斯束初至波波形反演. 地球物理学报, 57(9): 2900-2909, doi: 10.6038/cjg20140915.
(本文编辑 胡素芳)
Strategy and application of waveform inversion based on seismic data subset
DONG Liang-Guo, HUANG Chao, CHI Ben-Xin, LIU Yu-Zhu
StateKeyLaboratoryofMarineGeology,TongjiUniversity,Shanghai200092,China
The main difficulty in seismic full waveform inversion (FWI) is the strong nonlinearity, which is caused by the complexity of seismic wave propagation. Different components of elastic parameters result in different characteristics of seismic data. Meanwhile, different inversion accuracy is required in different stages of exploration or exploitation. So, it is really not necessary to pursue matching all the seismic information during the inversion. Some problems can be solved by matching part of seismic information and the strong nonlinearity can also be alleviated by this way. According to this consideration, a generalized FWI strategy and method based on seismic data subsets is presented. For different seismic data subsets, the gradients of the misfits have the same form and can be calculated by two modeling applications just as traditional FWI, and the only difference in calculating the gradients is the adjoint sources.During the waveform inversion based on seismic data subsets, the responses of seismic data to different scales of perturbation on different media parameters should be analyzed intensively. Different seismic data subsets should be used in different stages of full waveform inversion. And then the residual of this seismic data subset is back-projected along the reasonable sub-kernels to decide where and which component of the medium parameter need to be updated. As examples, envelope and reflection data subsets are used in FWI with synthetic and real data to prove the validity and effectiveness of our presented FWI strategy and method. Especially, in the absence of low frequency contents, reasonable misfits can be used to recover the background compressional and shear velocity using these FWI methods.
Full waveform inversion; Waveform inversion; Seismic data subset; Nonlinearity; Misfit function; Sensitivity kernel
10.6038/cjg20151024.
Dong L G, Huang C, Chi B X,et al. 2015. Strategy and application of waveform inversion based on seismic data subset.ChineseJ.Geophys. (in Chinese),58(10):3735-3745,doi:10.6038/cjg20151024.
国家油气重大专项(2011ZX05005-005-007HZ)和国家自然科学基金(41274116和41474034)项目资助.
董良国,男,同济大学海洋与地球科学学院教授,博士生导师,主要从事地震波传播理论与数值模拟、地震波反演等方面的研究. E-mail:dlg@tongji.edu.cn
10.6038/cjg20151024
P631
2015-01-15,2015-09-06收修定稿
董良国, 黄超, 迟本鑫等. 2015. 基于地震数据子集的波形反演思路、方法与应用.地球物理学报,58(10):3735-3745,
