风驱动优化算法

任作琳，张儒剑，田雨波

(1.江苏科技大学电子信息学院，江苏镇江212003)(2.南京邮电大学海外教育学院，江苏南京210046)

智能优化算法具有全局的、并行高效的优化性能、鲁棒性、通用性强、无需问题特殊信息等优点，已经被广泛应用于计算机科学、优化调度、运输问题、组合优化、工程优化设计等众多领域，并引起了国内外学者的广泛关注［1］.美国宾夕法尼亚州立大学电气工程系的Bayraktar Z和Werner D H博士以及气象学系的 Komurcu M博士在2010年IEEE Antennas and Propagation Society International Symposium上发表了名为“Wind Driven Optimization(WDO):A novel nature-inspired optimization algorithm and its application to electromagnetic”的论文［2］，标志着风驱动优化 (WDO)算法的诞生.

风驱动优化算法是一种基于群体的迭代启发式全局优化算法，该算法是基于对简化的空气质点受力运动模型的模拟.其核心是研究空气质点在大气中的受力运动情况，应用牛顿第二定律并结合理想气体状态方程，推导出空气质点在每一次迭代中的速度和位置的更新方程.该算法简单，易于实现，可调参数较少，能够有效跳出局部极值寻找到最优极值，可以处理多模和多维问题，也可以处理连续优化问题和离散优化问题.

相比于其他智能优化算法(如粒子群优化算法)该算法更新方程具有实际的物理意义，其全局搜索能力较强，收敛速度较快，寻优效率高，鲁棒性强，且可以通过微调系数达到不同的优化拓扑结构，应用前景十分广泛.目前国内刚刚开始关注WDO算法的研究，文中介绍了WDO算法的原理和目前的研究情况，进而给致力于研究WDO算法的研究者们提供一些借鉴.

1 风驱动优化算法

1.1 算法物理基础

大气动力学是经典力学中牛顿定律在地球大气中的应用，大气运动和经典流体力学的一个主要区别是:大气运动是处于一个旋转的地球表面上［3］.

众所周知，牛顿定律是在一个无加速度的坐标系(即惯性坐标系)中处理质点加速度与质点所受作用力之间的关系.若将这些定律应用于非惯性旋转坐标系中，就必须做一些相应的变化与调整.

在一个无加速度的惯性坐标系(或称绝对坐标系)中，一个单位质量气块运动的速度矢量以Va表示.按牛顿定律，它的加速度与所受到的力之间的关系可以表达为:

式中:下标a表示绝对坐标系，Fi为作用在气块上的力.

首先分析式(1)左端项.由于大气运动处于一个旋转的地球表面上，其运动的速度和加速度，从绝对坐标系(例如在恒星上)观察与从地球表面上观察是不同的，前者称为绝对速度和绝对加速度，后者称为相对速度和相对加速度.

设地球的旋转角速度为Ω，一个物体或空气块的绝对速度为Va，地球表面上观察的相对速度为V，则它们之间的关系为:

式中r为气块的位置矢量，其大小为地心至气块重心的距离，方向由地心指向气块.式(2)可以表示为:

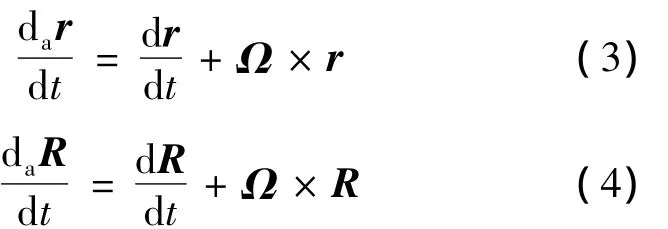
式中R为气块相对地球转动轴的位置矢量.

下述表达式对所有矢量普遍成立:

式中A为某一矢量.将式(2)代入式(5):

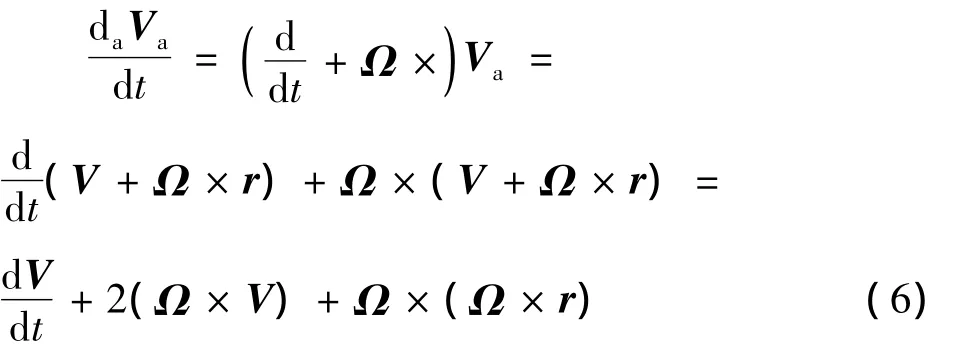
式(6)中最后一个等号右边第一项为相对于地球表面的加速度;第二项为科氏(Coriolis)加速度，只有当气块相对地表运动时(V≠0)才出现;第三项为气块随地球旋转而具有的向心加速度，只与气块位置(矢量r)有关，与其是否相对运动无关.

下面再分析式(1)右端项.在地球表面上，气块受到的力有:① 气块与地球之间的牛顿万有引力，可表示为g*;② 由于气压空间分布差异引起的气压梯度力 －2p/ρ，ρ为空气密度，p为空气压强;③由于空气分子粘性引起的内摩擦力ν22V，ν为运动分子的粘性系数，22为拉普拉斯算子.于是式(1)成为:

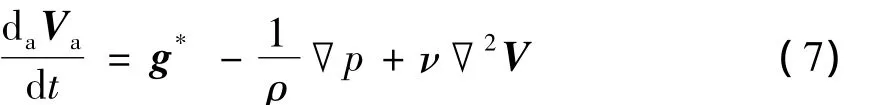
这是在旋转地球上的坐标系即非惯性坐标系中，气块加速度与作用在其上作用力之间的关系，即非惯性坐标系中的牛顿第二定律.其右端前3项仍保持原来的含义;第4项称为科氏力，在惯性坐标系中它本是物体的加速度，在非惯性坐标系中把它看成为力，所以称其为虚拟力.科氏力与地球自转轴垂直，并在北半球指向风矢量的右方.第5项也是虚拟力，称其为离心力.由于这个力只与位置有关，不将其作为单独的力看待，而是将其与引力项1合并，称为重力，即

式(10)即是单位质量气块加速度与作用在其上作用力之间的关系，亦即非惯性坐标系中的牛顿第二定律.

1.2 算法基本原理

地球大气的成分和结构是很复杂的，大气的任一微小部分(空气微团)可以作为“点”来处理，称为空气质点［4］.根据以上得出非惯性坐标系中的牛顿第二定律并结合理想气体状态方程，可以简化模型得出风驱动优化算法.

1.2.1 速度更新方程

世界气象组织(WMO)对于标准大气的定义中有这样的描述［2］:假定空气服从使温度、压力和密度与位势发生关系的理想气体定律和流体静力学方程.其中，大气处于流体静力平衡状态是指大气在垂直方向上受到重力和垂直气压梯度力的作用并达到平衡.在建模过程中，研究者并没有完全模拟大气运动，忽略了平流层离心力等微小影响的作用力，简化了建模，主要考虑4个力作用，并且假设空气质点处于流体静力平衡状态，且满足理想气体定律(即理想气体状态方程).又由于地球自转以及不同高度大气对太阳辐射吸收程度的差异，使得大气在水平方向比较均匀，而在垂直方向呈现明显的层状分布.所以，大气运动中水平运动对空气质点的影响强于垂直运动，在研究WDO算法中，仅需关注风的水平运动.由于研究对象是无限小的空气质点，可以假设空气质点为单位体积.虽然研究大气运动是在三维的世界里，但是算法应用可以映射到解决多维的问题中.

简化的牛顿第二定律及理想气体定律方程式如下:

式中:a为加速度，ρ为空气质点的密度，Fi为作用在空气质点上的力，P为压强，R为理想气体常数，T为温度.

由大气动力学知识可知，影响风吹动的主要力有4个，分别是:①启动空气质点运动的气压梯度力FPG，其方向由高压区指向低压区;②与FPG作用相反的摩擦力FF;需要指出的是，由于摩擦力的方程式较复杂，故在推导速度更新方程时应用另一种简化的表达方式;③ 垂直指向地心的重力FG，在物理学三维坐标系中假设地球的中心为直角坐标系的中心，那么可以认为重力是使空气质点移向坐标系原点的力，相似的将三维问题映射到N维中，重力代表指向坐标系中心的力;④ 地球旋转产生的科氏力Fc，它代表在每一次迭代中，空气质点当前所在维度中的速度和位置受其他任一维度的影响.4个力具体简化方程如下:

式中:－2P为气压梯度，负号说明沿梯度下降方向;δV为空气粒子的有限体积;α为摩擦系数，u为风速度矢量，g为重力加速度矢量，Ω为地球旋转角速度矢量.

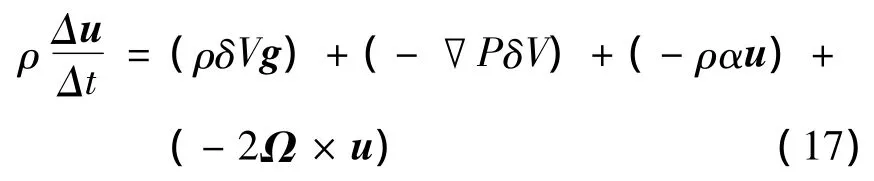
由于研究对象为无限小的空气质点，为了简化模型令δV=1，同时为了便于公式的推导，假定Δt=1，得到式(18):

将式(12)代入式(18)得到:

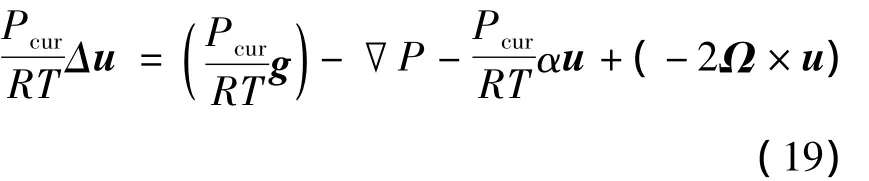
式中Pcur为当前位置空气质点的压力数值，将式(19)左右两边同时除以，得到:

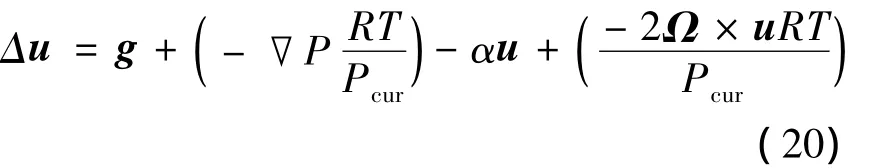
在风驱动优化算法中，空气质点速度和位置的每一次迭代都会发生改变，来探索新的搜索空间.因此，速度变量可以表示为Δu=unew－ucur，其中ucur为当前迭代中空气质点的速度，unew为下一次迭代中空气质点的速度.式(14)中，摩擦力的计算应用的是当前迭代速度值ucur，那么式(20)可以改写为:

根据重力定义，在一维坐标系［－1，1］范围中(图1a))表示空气质点的重力FG，则矢量g可以表示为g=|g|(0－xcur).

相似的由图1b)，FPG方向为空气质点从高压区指向低压区，即从当前位置指向最优压力点，那么 －2P可以表示为－2P=|Popt－Pcur|(xoptxcur)，Pcur为空气质点当前位置的压力值，Popt为种群中目前为止找到的最优压力值，xcur为当前位置，xopt为最优位置.式(21)中g和 －2P可以认为是由矢量图(图1a)和b))表示的两个矢量，并非物理定义的表达式，这样做的目的是为了简化方程，将式(21)中g和－2P写成标量与方向乘积形式，那么可以改写为:

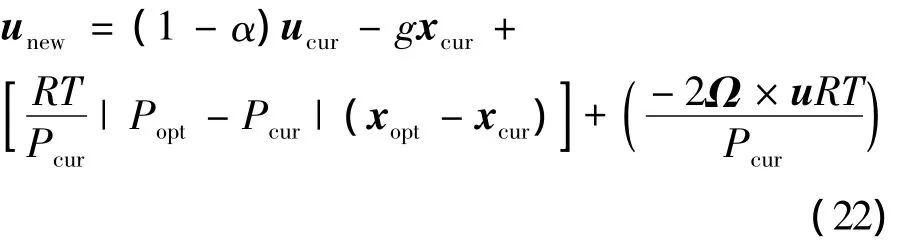
图1 一维坐标系中重力和气压梯度力Fig.1 Illustration of the gravitational force and the pressure gradient force in a one dimensional coordinate system

由科氏力Fc定义可知，它代表在每一次迭代中，空气质点当前所在维度中的速度受其他任一维度的影响，这个速度用uoctuhrerdim来表示.文献［2］为了简化方程定义设置了常数c=－2|Ω|RT，使得式(22)可以表示为:

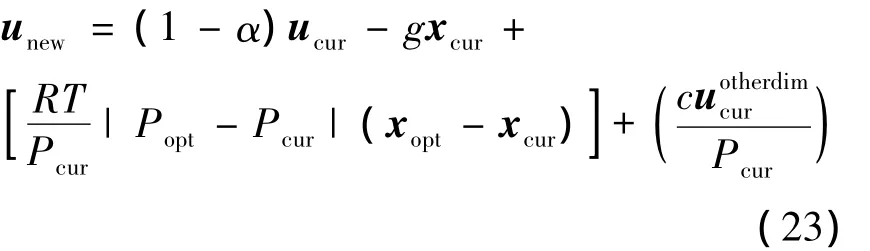
文献［2］中用式(23)作为速度更新方程，会因为引入压力值(Pcur和Popt)而使更新后的速度变得非常大，从而降低WDO算法的可操作性.相对于式(23)中使用的真实压力值，可以用i表示在所有空气质点中的一个降序排列，用来替换式子中的压力值(Pcur和Popt)，而在xopt最优位置时压力值最小，可设为1，那么式(23)可以改写为:

综上所述，式(24)为最后改进的速度更新方程，第一项表示在没有其它力作用在空气质点上时，摩擦力会使其速度在原路径上减小.可以使用固定的摩擦系数α，也可根据具体问题选择自适应的摩擦系数α，实验证明α一般取［0.8，0.9］.第二项表示空气质点从当前位置按常数g成比例向坐标系中心靠近，实验证明其取值范围为［0.6，0.7］.由于重力的存在，一定程度上避免了空气质点困在或跳出搜索边界，提高了全局搜索能力，加快了收敛速度.第三项促使空气质点移向最大压力点即全局最优位置，一般系数RT在［1.0，2.0］范围内.第四项模拟了科氏力，提供了其它维对当前维内空气质点速度的影响，增强了算法的鲁棒性，一般认为c取［0.05，3.6］.

1.2.2 位置更新方程

WDO算法是基于大气中空气质点运动的优化方法，每一次迭代过程中都要更新空气质点的速度和位置.已知速度更新方程式(24)，不难得出位置更新方程如下:假设时间间隔为Δt=1.

对于每一维中的空气质点，其搜索位置范围可以根据具体问题进行设定，其更新速度也具有一定的范围，可以简单将速度值大小作如下判断:

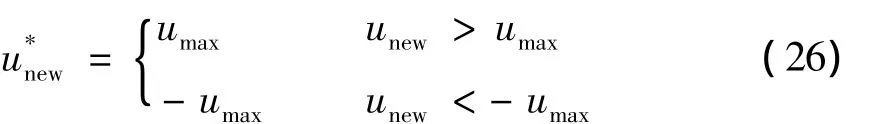
式中umax为速度边界值.

1.3 算法流程

为了描述方便清晰，表1列出了风驱动优化算法中用到的各个术语.

表1 风驱动优化算法相关术语及其描述Table 1 Terminologies used in the wind driven optimization algorithm and its descriptions

风驱动优化算法的流程如下:

1)初始化群体规模，设置最大迭代次数，相关参数(α，g，RT，c)，搜索边界以及定义压力函数(即适值函数);

2)随机初始化空气质点，随机分配起始速度和位置;

3)计算当前迭代中空气质点的压力值(适值)，并按照压力值将种群重新排列;

4)通过式(24)更新空气质点的速度;

5)通过式(25)更新空气质点的位置;

6)若未达到终止条件，则转3).

最后一次迭代过程中的压力值被记为最优结果.一般将终止条件设定为一个足够好的压力值(适应值)或达到一个预设的最大迭代代数.图2为风驱动优化算法流程.

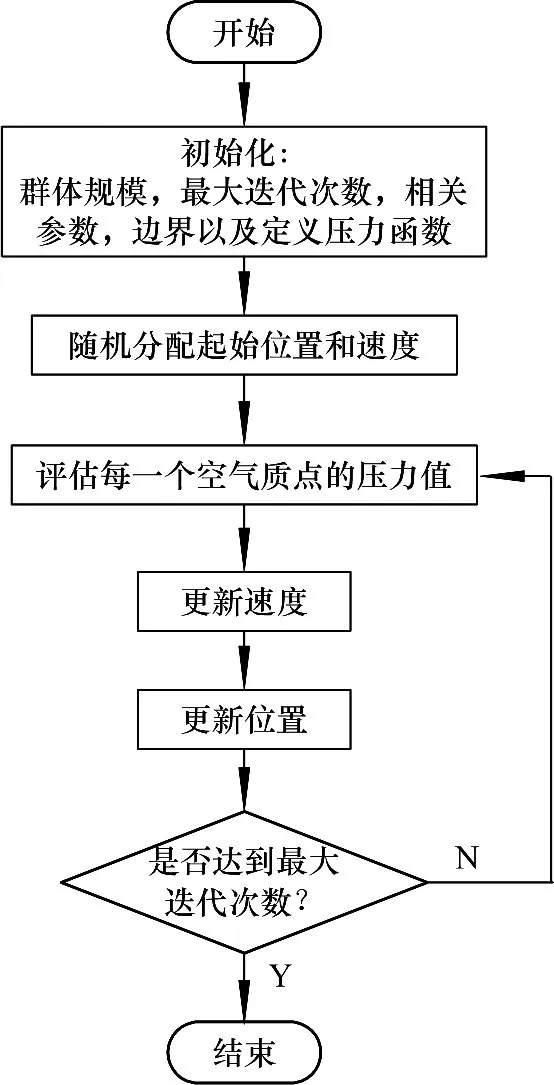
图2 风驱动优化算法流程Fig.2 Flowchart of the wind driven optimization algorithm

2 算法应用

风驱动优化算法是一种新型的全局优化算法，具有较强的鲁棒性，寻优效率高，既可以解决离散优化问题又可以解决连续优化问题.

2.1 WDO算法在电磁学问题中的应用

电磁优化问题大多都是非线性、多极值和不可微的复杂问题，一般的优化方法难以达到全局最优［4］.WDO算法因具有较强的全局搜索能力，并且可以处理离散优化问题，故可用于优化设计电磁学中的问题，目前主要解决三大类问题:天线阵综合问题，微带天线设计问题以及吸波材料设计问题.文献［5］中WDO算法研究了线性天线阵综合问题，并将WDO算法与粒子群算法(particle swarm optimization，PSO)、综合学习粒子群算法(comprehensive learning POS，CLPSO)作了比较，实验证明WDO算法的优化效果优于PSO算法和较复杂的CLPSO算法，更加证实了WDO算法的简单易行且高效的特性.文献［6］中应用WDO算法设计了两种微带天线，分别是E形微带贴片天线和加载短截线的倒F天线［7］.两个应用都证明了WDO算法针对设计和解决复杂的电磁学问题是一种高效的优化工具.在吸波材料设计问题上，文献［2，5，8］应用WDO算法设计了用于WiFi使用的复杂的双面人工磁导体表面材料(double-sided artificial magnetic conducting，DSAMC)，并与应用遗传算法(genetic algorthm，GA)算法设计的DSAMC作了比较，实验结果突出了WDO算法在电磁优化问题上的优越性，证明了WDO算法可以很好的解决离散优化问题.

2.2 WDO算法在图像处理问题中的应用

在图像处理方面，WDO算法也表现出了其强大的计算能力以及高效寻优的特性.图像分割技术是将图像分割成具有相似特性区域的过程，它是图像分析应用于模式识别和目标检测的领域中的一个重要步骤［9］.在卫星图像分割问题中，由于卫星图像的数据量大、特征信息丰富、背景复杂，使得精确分割卫星遥感图像是一项极具有挑战的任务.若想高效准确的找出图像分割合适的阈值就不得不进行大量的计算，而传统的优化方法表现出了局限性.文献［10］应用WDO算法基于卡普尔熵寻找卫星图像分割中的多层次阈值，实验证明WDO算法对于解决多层次阈值优化问题是十分合适且高效准确的，为WDO算法在图像处理领域的应用提出了一些方向，比如卫星图像增强，卫星图像分类以及其他卫星图像应用等.

2.3 WDO算法在其他问题中的应用

云计算是并行计算、分布式计算和虚拟技术相结合的产物，是当前计算机行业的技术热点，任务调度是云计算的核心技术之一，对云计算系统整体性能影响很大［11］.文献［12］基于微观经济学和WDO算法对云资源调度分配方案进行了设计，其应用WDO算法与GA算法结合法对云资源分配进行优化，在每一次迭代中，选择出最优个体，其余候选解依据Metropolis准则进行交叉、高斯变异操作，最后将进行过GA操作的候选解与最优个体整合得到当前迭代结果.实验结果表明，WDO算法的全局搜索能力较强.

3 总结与展望

风驱动优化算法是一种新近提出的全局群智能优化算法，该算法具有简单易实现、搜索效率高、收敛速度快等优点，文中对算法物理原理以及算法基本原理做出了详尽的介绍，并将近几年来国内外对该算法的应用研究进行了细致阐述.

目前该算法研究正处于起步和发展阶段，随着研究的深入，WDO算法必将在理论和实践应用上取得新的突破，现对其未来研究提出几点展望:

在算法理论研究方面:①算法的收敛性研究.对于任何优化算法，收敛性都是一个基本的研究问题，目前风驱动算法还缺少收敛性的理论研究.②算法关键参数的研究.目前算法参数的选择大多依据经验值选取，一些论文中给出了参数的选取范围，但针对不同问题，参数选取的不合适，则会大大影响寻优结果.如何根据具体问题，自适应地选取这些关键参数将是一个值得深入研究的内容.③算法与其他算法或技术的结合.为了不断完善风驱动优化算法的性能，增强其对不同问题研究的针对性，可以将其与成熟的智能优化算法或技术相结合，增强算法的寻优效率，同时也推进了对风驱动优化算法的研究.

在算法实践应用研究方面:开辟风驱动优化算法新的应用领域.与其他算法一样，应用是检验算法优劣的标准，是算法研究的价值体现.虽然WDO算法在电磁学领域应用广泛，但其在更丰富的工程应用中还未取得和其他智能算法一样的地位，研究该方法更广泛的实际应用将有着十分重要的意义.

References)

［1］ 刘琼.智能优化算法及其应用研究［D］.江苏无锡:江南大学，2011.

［2］ Bayraktar Z，Komurcu M，Werner D H.Wind driven optimization(WDO):a novel nature-inspired optimization algorithm and its application to electromagnetics［C］∥Antennas and Propagation Society International Symposium(APSURSI)，2010 IEEE，2010:1-4.

［3］ 盛裴轩，毛节泰，李建国，等.大气物理学［M］.北京:北京大学出版社，2003:30-48，168-169.

［4］ 高强，闫敦豹，袁乃昌.一种基于遗传算法的AMC结构设计［J］.电子学报，2006，34(9):1686-1689.Gao Qiang，Yan Dunbao，Yuan Naichang.A genetic-algorithm-based AMC structure［J］.Acta Electronica Sinica，2006，34(9):1686-1689.(in Chinese)

［5］ Bayraktar Z，Komurcu M，Bossard J A，et al.The wind driven optimization technique and its application in electromagnetics［J］.IEEE Transactions on Antennas and Propagation，2013，61(5):2745-2757.

［6］ 刘式适，刘式达.大气动力学(上)［M］.北京:北京大学出版社，2011:1-10.

［7］ Bayraktar Z，Komurcu M，Jiang Z H，et al.Stubloaded inverted-F antenna synthesis via wind driven optimization［C］∥ Antennas and Propagation(APSURS.l.)，2011 IEEE International Symposium on IEEE.［S.l.］:IEEE，2011:2920-2923.

［8］ Bayraktar Z，Turpin J P，Werner D H.Nature-inspired optimization of high-impedance metasurfaces with ultrasmall interwoven unit cells［J］.Antennas and Wireless Propagation Letters，IEEE，2011，10:1563-1566.

［9］ 丁知平.基于混合智能算法的卫星图像分割技术研究［J］.计算机测量与控制，2012，20(5):1420-1422.Ding Zhiping.Satellite image segmentation based on hybrid intelligent algorithms［J］.Computer Measurement＆ Control，2012，20(5):1420-1422.(in Chinese)

［10］ Bhandari A K，Singh V K，Kumar A，et al.Cuckoo search algorithm and wind driven optimization based study of satellite image segmentation for multilevel thresholding using Kapur′s entropy［J］.Expert Systems with Applications，2014，41(7):3538-3560.

［11］ 陈海燕.基于多群智能算法的云计算任务调度策略［J］.计算机科学，2014，41(6A):83-86.Chen Haiyan.Task scheduling in cloud computing based on swarm intelligent algorithms［J］.Computer Science，2014，41(6A):83-86.(in Chinese)

［12］ Sun J，Wang X，Huang M，et al.A cloud resource allocation scheme based on microeconomics and wind driven optimization［C］∥ChinaGrid Annual Conference(ChinaGrid)，2013 8th IEEE.［S.l.］:IEEE，2013:34-39.