探地雷达信号的EEMD时域分析方法
2015-03-07许军才刘立桥任青文沈振中
许军才, 刘立桥, 任青文, 沈振中
(1.河海大学 力学与材料学院,江苏 南京 210024;2.江西省数字国土重点实验室,江西 南昌 330013;3.无锡市水利设计研究院有限公司,江苏 无锡 224000)
探地雷达是无损检测中重要的探测方法,具有探测分辨率高、探测速度快、无污染等特点,在实际检测工程中得到了广泛的应用[1]。探地雷达信号处理水平对目标源的识别与定位起着决定作用,研究探地雷达信号处理方法具有重要的研究价值和现实意义。传统的傅里叶分析方法对平稳信号具有很好的处理效果,但傅里叶变换只能反映其在时频域范围的全局特征,并不能反映信号的时变特性,而且对非线性的时频信号也不能进行很好的识别。文献[2]提出的希尔伯特-黄变换(Hilbert-Huang)突破了Fourie分析的局限,该方法通过经验模态分解(empirical mode decomposition,EMD)将任意的信号分解为本征模态函数(intrinsic mode function,IMF),对处理非线性的时频信号能取得较好的效果。文献[3-4]将EMD方法用以提取地球物理方法中的非线性与非稳态信号。文献[5]将EMD方法用以处理探地雷达信号。EMD方法虽然有很多优点,但在处理数据过程中会出现模态混叠的缺点,学者们提出很多改进方法,其中以集合经验模态分解(ensemble empirical mode decomposition,EEMD)方法最为典型[6-7],本文在此基础上提出了基于EEMD的探地雷达信号时域分析方法。
1 EEMD原理
1.1 EEMD原理
通常在利用EMD方法分离过程中,除分离出来的特征模量1(IMF1)外其余的功率谱带通特性相同,前一个特征模量的值是后一个的2倍,在信号不是纯噪声时,分离的模量会产生模态混叠现象。由Flandrin为首的研究小组和Huang研究小组发现,采用EMD方法处理白噪声过程中,该方法可以把白噪声中均匀分布的不同频率信号分离开来[8],EEMD方法根据这一规律,将处理信号中加入白噪声,再由EMD方法把不同频率的信号分离开来,其分解步骤如下:
(1)初始化总体平均次数M,将加入的白噪声添加数值幅度,令i=1。
(2)把一个给定幅度的白噪声ni(t)加到原始信号x(t)中,组成一个新的信号xi(t),即
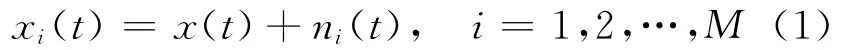
其中,xi(t)为第i个附加噪声信号;ni(t)为第i个系列的白噪声。
(3)使用EMD算法分解新生成的信号,xi(t)为IMF之和,其计算公式为:
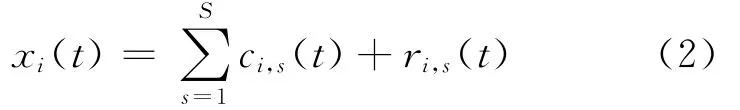
其中,s为IMF的数量;ri,s(t)为参与函数,代表信号的平均趋势;ci,s(t)为IMFs;(ci,1,ci,2,…,ci,s)包括从高到低不同范围频段的IMF分量。
(4)重复步骤(2)和步骤(3)至M次,则每次分解加入给定幅值不同的白噪声信号得到IMF的集合为:

(5)计算相应分解的IMF集合的平均值作为终值,EEMD分解得到的IMF为:
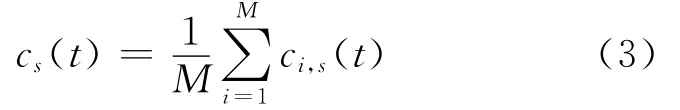
1.2 EMD与EEMD结果比较
本文以一正弦信号为例,其中x(t)=sin(πt/10)为雷达天线发出波形的信号,y(t)=(sin 5πt)/5为周期性的脉冲干扰信号,分别采用EMD和EEMD 2种方法分析,结果如图1、图2所示,其中在EEMD分解中噪声幅值取系数为0.02,总体平均次数取200,图1中显示特征模态分量未能分离出来,2种模态形成混叠。由图2可知,特征模态IMF1~IMF7中频率由高到低,各模态之间特征分界明显,没有出现图1中模态混叠情况。因此,EEMD能克服EMD有关的模态混叠现象。

图1 EMD分解图
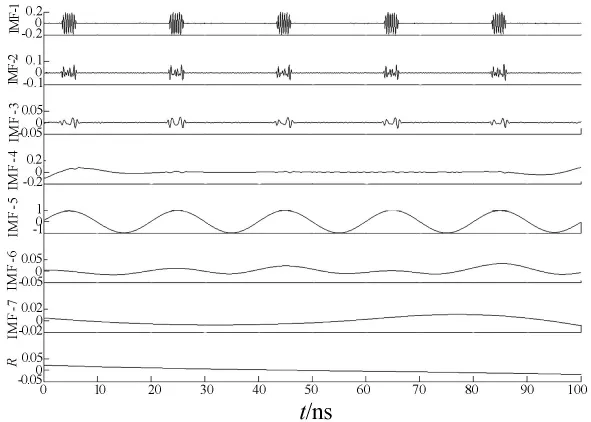
图2 EEMD分解图
2 EEMD多尺度分析与去噪
模型试验以在潮湿的沙土中埋置几种不同直径与深度的圆柱体为例,该圆柱体为钢筋和空管,模型尺寸与大小如图3所示,实验模型用以正演模拟出钢筋与空管形成的探地雷达信号。
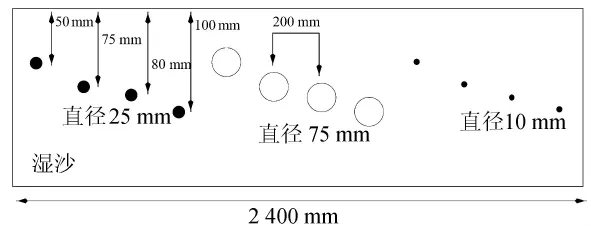
图3 探地雷达正演模型
沙土介电常数为20,电导率为0.1S/m,钢筋介电常数为1,电导率为106S/m,计算区域大小为2.5m×0.2m,计算网格大小为0.002 5m,时窗为12ns,以Ricker波作为激励,主频为900MHz,天线收发距为0.025m,模拟采样125道。通过时域有限差分(finite difference time domain,FDTD)方法正演出探测结果[9],如图4所示。
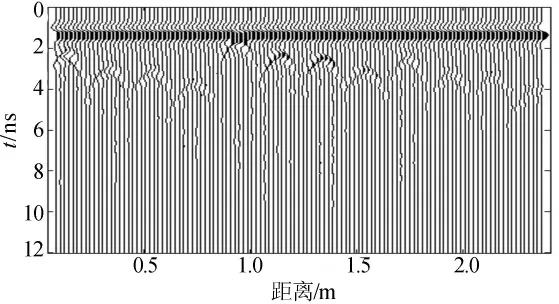
图4 模型正演计算剖面图
2.1 正演模型信号IMF分解
由正演模型得出的信号,可利用EEMD方法对探地雷达波信号进行多尺度分析。计算过程中,噪声幅值系数取0.2,总体平均次数取200,通过EEMD方法分解出IMF1~IMF8特征模态分量如图5所示。
从图5可看出,IMF1~IMF3信号频率较高,主要是高频干扰信号以及在计算过程添加的辅助噪声引起的,IMF4中能看到浅部圆柱体产生的明显反射弧,IMF5中能识别出更深一些的圆柱体激发的反射弧,在IMF6模态分量中能看出各个圆柱体产生的反射弧,IMF7由圆柱体激发的反射弧有所减弱,IMF8主要是由深部的超低频信号组成。目标源产生的信号主要集中在IMF5、IMF6与IMF7特征模量中。
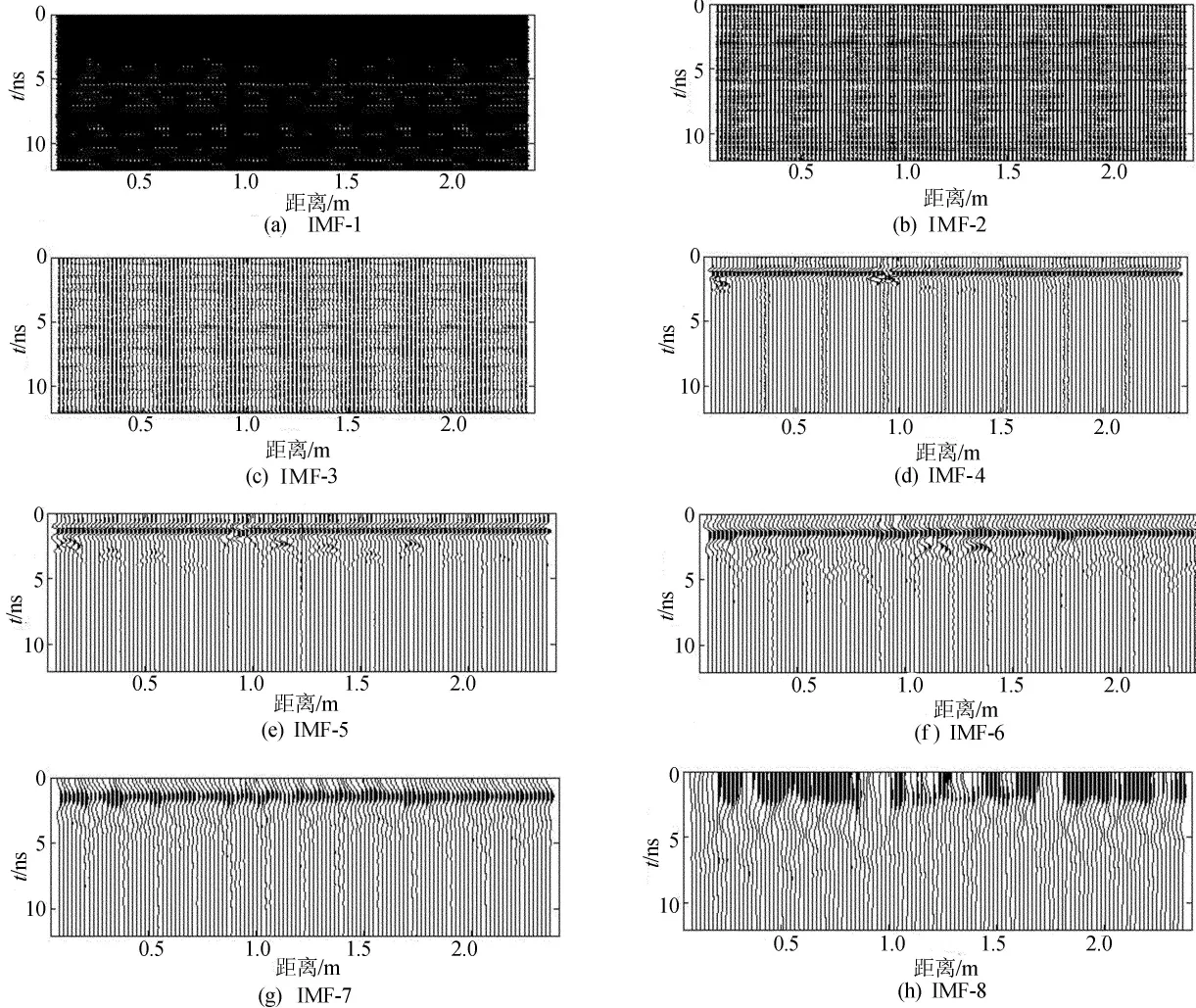
图5 IMF1~IMF8分量结果
总体来看,IMF1~IMF3由高频干扰信号组成,IMF4~IMF7为下方目标探测体激发的反射信号,IMF8本征模态分量主要由深层的低频信号组成。从分离结果来看,EEMD方法可以很好地将目标源与非目标体产生的信号在不同的尺度上分离开来。
2.2 EEMD去噪分析
为验证EEMD的去噪能力,在正演信号中,加入白噪声背景信号,将图4中原始信号加入白噪声信号如图6所示,图6中雷达信号的异常受到白噪声的干扰,有效信号被淹没在噪声中,很难识别出目标源产生的反射弧。
将图6中掺杂有噪声的信号,利用EEMD方法分离出特征模态分量,再将以目标信息为主的特征模态分量叠加来压制噪声干扰,从而提高目标信号的分辨能力,本文将IMF6与IMF7相加得出2个特征模量的合成信号,利用EEMD去噪后的结果如图7所示。

图6 加入白噪声后的信号

图7 EEMD去噪后的信号
从图7可看出,由圆柱体产生的反射弧利用EEMD能有效地将噪声从探测信号中分离出去,处理后的结果能清晰识别目标信号。
3 结 论
EMD方法由于其本身的缺陷,在处理信号过程中会出现特征模量的模态混叠弊病[10],本文比较了EMD与EEMD 2种方法对电磁信号的处理效果,并研究了EEMD方法对探地雷达信号时域的处理效果,通过研究分析得出以下结论:
(1)EEMD方法在处理电磁信号过程中能克服EMD方法的模态混频的不足,能有效地将不同的特征模量分离开来。
(2)EEMD方法分离出的探地雷达特征模量中,IMF1、IMF2、IMF3主要由高频干扰和辅助噪声信号组成,目标源产生的主要集中在IMF4~IMF7中,目标源产生的信号随特征模量序号的增加逐渐反映深部目标源的反射信号。
(3)EEMD方法能分离出信号中的干扰源与目标源形成的各自特征模量,通过合成目标源形成的特征模量,能有效对干扰信号进行压制,提高对目标源信号分辨率能力。
[1] 王中有,陈振富,孙 冰,等.探地雷达技术在混凝土结构中的应用与研究[J].混凝土,2013(12):138-141.
[2] Huang N E,Attoh-Okine N O.The Hilbert-Huang transform in engineering[M].Ablingdon:Taylor & Francis Ltd,2005:1-2.
[3] Huang N E,Wu Z.A review on Hilbert-Huang transform:method and its applications to geophysical studies[J].Reviews of Geophysics,2008,46(2):1-23.
[4] Chen C,Jeng Y.Nonlinear data processing method for the signal enhancement of GPR data[J].Journal of Applied Geophysics,2011,75(1):113-123.
[5] Feng D,Chen C,Yu K.Signal enhancement and complex signal analysis of GPR based on Hilbert-Huang transform,in electrical power systems and computers[M].Baseli:Springer,2011:375-384.
[6] Lei Y,He Z,Zi Y.EEMD method and WNN for fault diagnosis of locomotive roller bearings[J].Expert Systems with Applications,2011,38(6):7334-7341.
[7] Jiang H,Li C,Li H.An improved EEMD with multiwavelet packet for rotating machinery multi-fault diagnosis[J].Mechanical Systems and Signal Processing,2013,36(2):225-239.
[8] 汪家慰,刘正士,王 慧.HHT法识别结构模态频率和阻尼比的改进[J].合肥工业大学学报:自然科学版,2010,33(5):647-651.
[9] Wang Y,Yeh C,Young H,et al.On the computational complexity of the empirical mode decomposition algorithm[J].Physica A:Statistical Mechanics and its Applications,2014:400(2):159-167.
[10] Giannopoulos A.Modelling ground penetrating radar by GprMax[J].Construction and Building Materials,2005,19(10):755-762.
