基于最小生成树的立体匹配算法

李智鹏， 宋 勇， 余 烨， 何小旭， 聂振兴

（1.四川航天系统工程研究所，四川 成都 610000；2.合肥工业大学 计算机与信息学院，安徽 合肥 230009）

0 引 言

自20世纪80年代第1个计算机视觉系统框架被提出以来，立体匹配一直是计算视觉研究领域的热点。文献［1］将立体匹配算法归为全局算法和局部算法2大类，并将立体匹配算法分为以下4个步骤：① 匹配代价计算；② 代价聚合；③视差最优化；④ 视差细化。

全局算法主要是采用全局最优化的思想估计视差值，它需要一个全局的能量函数，通过最小化全局能量函数得到最优的视差值，它没有代价聚合的过程。这种方式能够得到准确度非常高的视差图，但是计算开销大、费时，不能运用于实时系统。文献［2］提出了图割算法进行立体匹配，采用最大流、最小割理论计算最佳视差值；文献［3］提出了基于置信传播的立体匹配算法，采用马尔科夫网络计算最大后验概率从而得到最优视差；文献［4］提出了基于神经网络的匹配算法，通过边缘特征在3个约束下的对应关系构建目标函数，采用分级提取边缘的思想实现实时匹配；文献［5］引入了水平和垂直方向不连续的最小约束到动态规划算法中，有效地提高了匹配的速度。

局部算法依赖于兴趣点相关邻域内的像素对其加权聚合，计算简单、效果适中，适用于实时系统，但是对噪声敏感，在遮挡区域匹配效果不好。文献［6］提出一种单向匹配算法，利用极限约束只从左到右匹配1次，并且从数学的角度提出了优化的计算策略，极大地提高了匹配速度；文献［7］提出了一种基于窗口的自适应权重立体匹配算法，通过相似性自适应地调整窗口中权值的大小，在局部算法中取得了良好的效果；文献［8］利用视差图的分段连续性，将像素点分为特征点和非特征点，提出了一种快速双目立体匹配算法，但是线条特征明显，在视差渐变处精度一般；文献［9］利用双边滤波的思想，提出了一种non－local的快速代价聚合方法，能够得到平滑高精度的视差图；文献［10］利用图像分割的思想，提出了分割树的匹配算法，能够得到高精度的视差图，但是计算复杂度非常高；文献［11］没有关注匹配代价计算和代价聚合，而专注于视差细化的过程，实验效果相当显著，证明了视差细化的重要性；文献［12］添加了多因素的影响，改进了自适应权重匹配算法，增加了匹配的准确性。

鉴于对立体匹配算法的快速性和准确性需求，在前人研究的基础上，本文提出了一种基于最小生成树的立体匹配算法。它采用双边滤波的思想，在代价聚合中将整幅图像向兴趣点聚合，并在视差细化方面采用了相似的方式进行滤波，使得聚合和细化能够有效结合，提高了匹配的精度，加快了算法整体的速度。

1 算法介绍

立体匹配最终要得到平滑、准确、稠密的视差图，研究的关键问题是求取视差。代价聚合是利用邻域中像素点的匹配代价加权和来计算中心像素点的最终代价，聚合将当前点的匹配代价向周围传递，以达到纠正错误匹配即滤波的目的，所以代价聚合实质上也是一个滤波的过程。而视差图有许多深度不连续区域，某些滤波器在滤除噪声的同时也会将一些边缘区域模糊掉，所以采用保边去噪的双边滤波器是一个很好的选择。一般的双边滤波器是在一个子区域内进行加权滤波的。局部立体匹配算法也是在一个子区域内进行聚合的，相关窗口的选取影响着匹配的快速性和准确性。局部算法寻找最佳匹配点是一个局部最优化过程，受到局部特征的影响，它的局限性在于针对弱纹理和遮挡等区域无法有效地找到正确匹配点。为了弥补这种缺陷，本文提出了一种新的算法，是在双边滤波的基础上增加了最小生成树的结构改进，算法流程如图1所示。

图1 算法流程图

每个步骤的说明如下：

（2）代价聚合。本文将图像上的所有点都向兴趣点聚合，计算出新的匹配代价。在这里本文引入了双边滤波和最小生成树。双边滤波具有保边去噪的特性，并且能够产生自适应的权值。最小生成树能够使得整体的匹配代价最小，还能够对图像中所有像素点进行层次性的划分，使得所有点的的聚合有了统一的标准。其他点对兴趣点的权重支持依赖于最小生成树上它们之间的最短路径。

（3）计算视差值。本文采用WTA优胜者全选的方式，每一个视差值都有一个最终的匹配代价，WTA就是选取最小匹配代价对应的视差值为兴趣点最终的视差。

（4）视差细化。优化视差图，验证舍去错误匹配点，本文采用与代价聚合相似的方式，通过图像所有点来验证。

与其他的局部算法相比，该方法计算简单，没有复杂的数学公式，没有涉及到相关窗口，计算复杂度为ο（HWdmax）。

本文特色在于将最小生成树引入代价聚合和视差细化。

1.1 自适应权值的代价聚合

本文将图像看成一个无向图G（V，E），则图像上的像素点为无向图的顶点v，相邻像素点的差值为相邻顶点的权值w。此无向图G（V，E）中有若干回路，不便于聚合，本文采用Kruskal算法将其转化为最小生成树，这样去除回路后既简化了聚合过程，又能使整体的聚合代价最小。本文将左上角第1个像素点约定为树的根节点，父子节点关系使树结构化，从而进一步简化聚合过程。

骨折是常发生的一种意外事故，对于患者的身心健康、以及日常生活都带了极大的影响。患者在治疗过程中会产生较大的疼痛感，药物镇痛难以完全缓解患者的这种疼痛，为了一定程度上缓解患者的疼痛感，我院特对骨科患者实施了无痛护理，经临床研究发现，应用无痛护理效果极佳。具体的研究分析报告如下。

代价聚合针对的是匹配代价，匹配代价在聚合之后要进行最优值比较，所以双边滤波能够进行改造，即

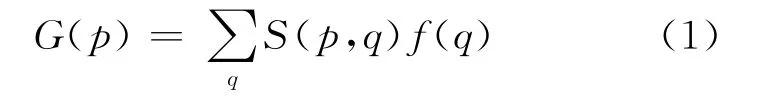
改造的结果既能省略平均过程、简化计算，又不影响比较的结果。其中，G（p）为滤波器输出；f（q）为滤波器输入；权值S（p，q）为：

其中，Dis（p，q）表示最小生成树上p、q2点的最短路径；σ为一个常数。（2）式是一个权重传递的过程，体现了双边滤波思想中位置与像素值2方面的变化。本算法对于兴趣点的代价聚合值计算公式如下：

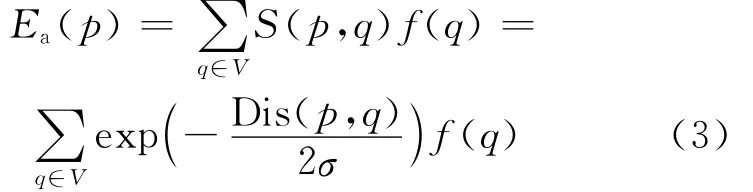
其中，Ea（p）为来自图像上所有点的代价聚合支持值；V为所有像素点的集合。

1.2 简化聚合步骤及证明

本文发现每一个点的代价聚合值只与它的父节点和子树有关，这又进一步简化了代价聚合的复杂度。

证明

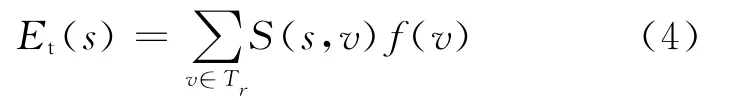
其中，Tr为s点下的一颗子树；r为子树Tr的根节点；点v为子树Tr里的任意一点；S（s，v）为点s和点v之间的权重系数；Et（s）为点s的子树对它的聚合。

（4）式可转换为：

（5）式表示点s的子树对它的聚合Et（s）可以转化为子树上所有点对子树根节点的聚合值与根节点r对点s的权重支持S（s，r）的乘积。

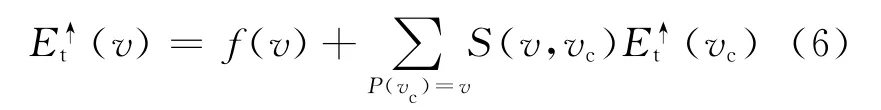
其中，（v）为点v下子树中所有节点对它的聚合支撑，v∈Tr；P（vc）为点vc的父节点。如果点v为叶子节点，则（v）＝f（v）；如果点v为根节点，则（v）＝Ea（v）。

现有一树结构，如图2所示。

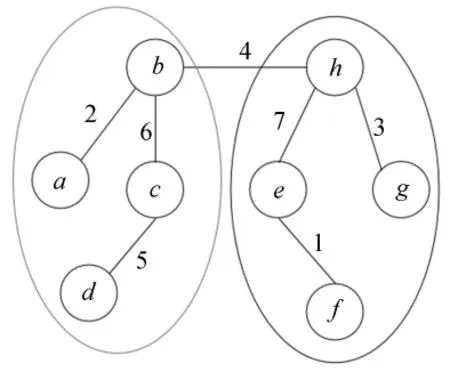
图2 树的结构示意图

图2中，所有节点对点h的代价聚合值Ea（h）为：

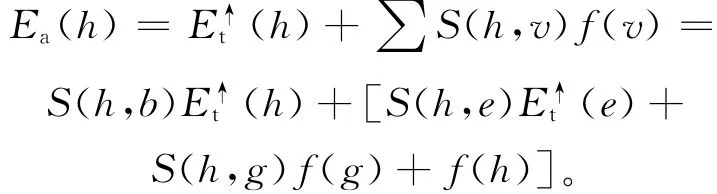
图2中，左框里的点对点h的代价聚合值为S（h，b）（b），则右框里的点对点h的代价聚合值为Ea（h）－S（h，b）（b）；由（5）式可知，右框里的点对点b的代价聚合值为：

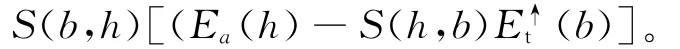
综上所述可知：

其中，点b、h为1对邻接点，在有向树中也就是父子节点的关系。将上述关系推导成有向树中的一般情况为：

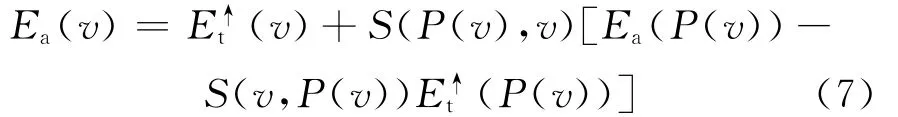
其中，P（v）为点v的父节点。（7）式表明，最小生成树上所有点对兴趣点的聚合值只与其父节点的聚合值和其子树上所有点的聚合支撑值有关。

1.3 视差细化

视差细化主要是进行一些子像素级的视差估计、交叉验证和一些后续处理。

子像素视差估计主要是采取一些曲线拟合的方法产生亚像素级的视差，以此来提高立体匹配之后三维建模或测量的精度。

交叉验证是在确定判断遮挡区域像素点之后，重新估计它们，常用中值滤波进行细化。

中值滤波在去除椒盐噪声上取得了很好的效果，但它会使边缘模糊化。

本文算法中细化过程着重于优化实验结果，采用双边滤波进行视差细化。代价聚合和视差细化本质上都是滤波的过程。本文视差细化的方式也是依靠于双边滤波的思想，采用了前文代价聚合类似的方式，计算公式如下：

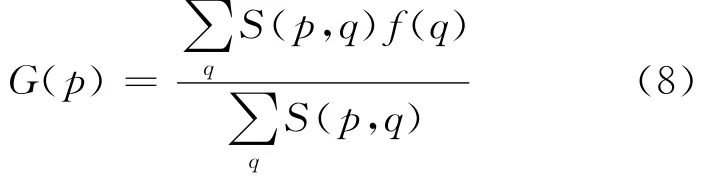
在代价聚合过程中，针对的是匹配代价，需要匹配代价的比较结果。视差细化针对的是视差值，需要重新估计视差，加权后多出了平均的过程。这种细化方式既可以利用双边滤波器保边去噪的的特性得到更加平滑的视差图，又可以利用前述的简化过程加快速度，使得视差细化和代价聚合联系得更加紧密。

2 实验结果

采用Middlebury大学立体匹配算法评测网站上提供的标准数据集Tsukuba、Venus、Teddy和Cones作为实验对象，选取常数σ分别为0.10、0.18、0.22、0.22，得到本文算法与几种经典算法的实验结果如图3所示。

图3 本文算法与几种经典算法在标准数据集上的实验结果

由图3可以看出，本文算法得到的视差图比经典的图割算法更加平滑，平滑程度非常接近于文献［7］和理想图。文献［7］的实验结果目前在国际上排名比较靠前，具有参照价值。

Middlebury大学立体匹配算法评测平台是国际公认的标准平台，本文算法和几种经典算法在该平台上的评测结果见表1所列。其中，nonocc为遮挡区域的误匹配率；all为整体的误匹配率；disc为视差不连续区域的误匹配率。表1中，本文算法Ⅰ为本文视差图的真实评测结果；而在实际中，通常对中间区域的匹配结果更感兴趣，因此本文算法Ⅱ为截取本文结果的中间部分进行评测的结果。从表1可以看出，本文算法相比于文献［2］误匹配率有所减少，与文献［7］相比，某些情况误匹配率有所降低。本文算法的运行环境为Inter i3－2120＠3.4GHz、8G内存。

表1 本文算法与几种经典算法的误匹配率 %

表2所列为各个算法的运行时间，经过比较本文算法在各个数据集上的运行时间都是最小的。

表2 本文算法与几种经典算法运行时间的比较 s

实验表明，本文提出的匹配算法能够快速、有效地得到平滑准确的视差图，它的中心区域与理想情况非常接近，能够达到较低的误匹配率，与其他算法相比运行速度也得到了很大的提高，可以运用到实际系统中。然而本文算法的不足是在边缘处未能得到很好的效果，边缘处效果的改进也是后续工作的重点。

3 结束语

本文提出了一种基于最小生成树的立体匹配算法，它本质上是一种局部算法，但是摒弃了相关窗口，没有关注兴趣点的邻域，而是让图像中的所有点都向兴趣点进行聚合，结合了整体特性。本文还提出了简化的计算方法，时间复杂度降到了ο（HWdmax），极大地提高了计算效率。实验结果表明，本文的算法能够快速得到平滑准确的视差图，并且能够运用于实时系统。

［1］ Scharstein D，Szeliski R.A taxonomy and evaluation of dense two－frame stereo correspondence algorithms［J］.International Journal of Computer Vision，2002，47（1／2／3）：7－42.

［2］ Roy S，Cox I J.A maximum－flow formulation of the n－camera stereo correspondence problem ［C］／／International Conference on Computer Vision.IEEE，1998：492－499.

［3］ Sun Jian，Zheng Nanning，Shum H Y.Stereo matching using belief propagation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2003，25（7）：787－800.

［4］ Ruichek Y.Multilevel－and neural－network－based stereomatching method for real－time obstacle detection using linear cameras［J］.IEEE Transactions on Intelligent Transportation Systems，2005，6（1）：54－62.

［5］ Cox I J，Hingorani S L，Rao S B.A maximum likelihood stereo algorithm［J］.Computer Vision and Image Understanding，1996，63（3）：542－567.

［6］ Stefano L D，Marchionni M，Mattoccia S.A fast area－based stereo matching algorithm［J］.Image and Vision Computing，2004，22（12）：983－1005.

［7］ Yoon K J，Kweon I S.Adaptive support－weight approach for correspondence search［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2006，28（4）：650－656.

［8］ 狄红卫，柴 颖，李 逵.一种快速双目视觉立体匹配算法［J］.光学学报，2009（8）：2180－2184.

［9］ Yang Q.A non－local cost aggregation method for stereo matching［C］／／IEEE Conference on Computer Vision and Pattern Recognition.IEEE，2012：1402－1409.

［10］ Mei Xing，Sun Xun，Dong Weiming，et al.Segment－tree based cost aggregation for stereo matching［C］／／IEEE Conference on Computer Vision and Pattern Recognition.IEEE，2013：313－320.

［11］ Ma Ziyang，He Kaiming，Wei Yichen，et al.Constant time weighted median filtering for stereo matching and beyond［C］／／IEEE International Conference on Computer Vision.IEEE，2013：49－56.

［12］ 何 川，余 烨，段瑞青，等.一种基于多因素的自适应支持权重匹配算法［J］.合肥工业大学学报：自然科学版，2013，36（7）：798－801，878.