车辆动载对路面的永久变形损伤评价

张宗涛， 朱月风， 张洪亮

（长安大学 特殊地区公路工程教育部重点实验室，陕西 西安 710064）

0 引 言

随着我国高等级公路的发展，重型汽车已成为主要的交通工具。交通荷载和交通量的增加加速了路面的破坏，作为目前路面的三大破坏之一的永久变形，尤其严重。目前，在研究路面永久变形损伤时，通常只对永久变形产生机理及永久变形预测进行研究［1］，对车辆动荷载条件下的路面永久变形损伤评价并不多。研究车辆荷载条件下路面永久变形损伤程度，可为道路管理者提供重要的理论支持，如交通量的控制、车速的限制、路面养护时机和车辆超载的限制等。

路面不平度是产生车辆动载的直接原因，因此路面不平度的模拟是车辆对路面永久变形损伤的关键。路面谱估计主要有经典谱估计法和现代谱估计法，现代谱估计法由于其性能好，谱分辨率高而得到了广泛的应用［2－6］。而现代谱中应用最广泛的为自回归（auto regressive，AR）模型，文献［7－8］采用AR模型拟合路面不平度功率谱密度，计算量都较小，能较好地逼近理论值，模拟精度较高。车辆动载是由于车辆受到路面的不平度激励产生的，它与车速、路面不平度、车辆的振动系统等有直接关系。近年来，车辆动荷载受到了广泛的关注，对于动荷载的时域模拟，文献［9］采用快速傅里叶逆变换对路面随机不平度进行了时域模拟，并分析了不同路面等级、车速、质量等参数对路面受到的动荷载的影响规律；文献［10－11］用ADAMS软件对车辆动态力进行仿真，用虚拟样机模拟车辆动荷载的变化规律。

在评价车辆动载对路面的损伤时，美国国家高速公路和交通运输协会（AASHTO）通过大量实验得出四次方定律，即车辆对沥青路面的疲劳损伤与车辆静态轴载的四次幂成正比。文献［12］提出动荷载系数（DLC）的概念，认为车辆在正常行驶时，DLC一般为0.1～0.3；文献［13］采用路面疲劳损伤的四次方定律，得到瞬时车轮力四次方的期望值，提出了道路应力因子的概念；文献［14］通过实际调查提出动态作用力沿轮迹分布具有空间重复性，认为轮胎作用力会集中在沿路面的某些特定位置，路面的疲劳损伤就达到某一轮胎力的4倍；文献［15］采用车辆满载和超载时的加权四次方定律来评价车辆对路面的损伤；文献［16］采用全概率评价方法，从车辆行驶的整个过程去评价车辆对道路的损伤。

本文提出车辆动载对路面永久变形损伤指标，研究了沥青路面在行车动载下的永久变形损伤，对控制车速、路面维修养护具有一定意义。

1 路面功率谱密度

路面功率谱密度［17］的拟合公式为：

其中，Gq（n）为路面不平度空间频率功率谱密度，简称路面功率谱密度；n为空间频率；参考空间频率n0＝0.1／m；Gq（n0）为参考空间频率n0下的路面不平度空间功率谱密度，称为路面不平度系数；W为频率指数，决定路面功率谱密度的频率结构。

但在试验与实际中，一般采用时域信号进行模拟，所以有必要将空间功率谱密度转化为时间功率密度，具体公式为：

其中，Gq（f）为时间功率谱密度；f为时间频率；u为车速。

2 AR模型的建立

其中，输出序列x（n）为平稳随机过程；输入序列u（n）通常为白噪声序列、平稳随机过程，均值为0，方差为σ2；p为 AR模型的阶数；a（k）（k＝1，2，3，…，p）为AR模型的参数。

对（3）式进行Z变换，可得：

现代谱估计中比较常见的时间序列模型——AR模型得到了广泛的应用［7－8］。AR模型的定义为：

其中，H（z）为x（n）和u（n）之间的系统函数；X（z）为x（n）的Z变换；U（z）为u（n）的Z变换。

对平稳随机信号进行线性系统的理论分析，x（n）的功率谱密度用归一化频率表示为：

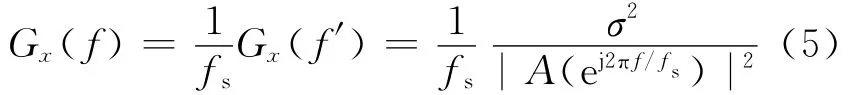
其中，fs为采样频率；f为时间频率；f′为归一化频率。

2.1 路面随机激励AR模型的实现算法

建立AR模型路面随机序列时，参数a（k）（k＝1，2，3，…，p）的确定是试验应用中的关键。根据（2）式，在给定路面等级及车速的情况下，给定离散的频率fk＝kΔf，k＝1，2，3，…，N－1，得到离散的路面随机激励时间功率谱密度Gq（fk）。并可以得到与Gq（fk）所对应的路面随机激励的自相关性函数序列Rq（m）为：

构造Yule－Walker函数，预选阶数为l，得到l阶AR模型和自相关函数关系式为：

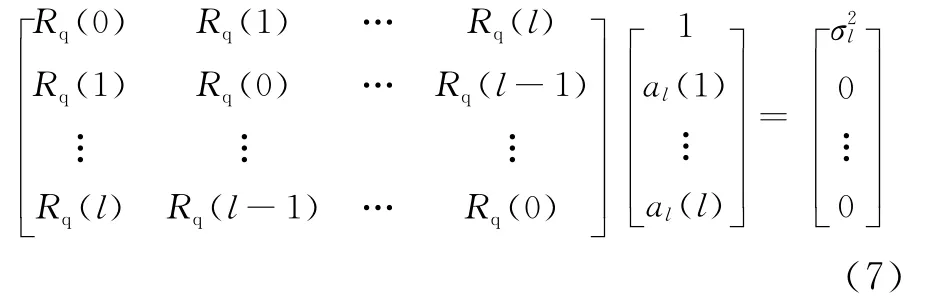
利用Levinson－Durbin算法对路面AR时域模型参数进行求解，得到｛al（1），al（2），…，al（l），ρl｝，且输入序列的白噪声序列u（n）方差σ2＝ρl。所以输入序列l阶AR模型的白噪声序列u（n）可表示为：

其中，w（n）为标准正态分布随机变量。

将｛al（1），al（2），…，al（l），ρl｝和u（n）带入（3）式可得时域模型路面随机激励样本x（n）为：

2.2 路面AR模型的建立

利用Burg法对路面随机激励样本x（n）的AR模型参数进行估计，得到模型参数的估计值｛a1（1），ρ1｝，｛a2（1），a2（2），ρ2｝，…，｛aN－1（1），aN－1（2），…，aN－1（N－1），ρN－1｝。

利用预测误差准则和阿凯克信息论准则，取AR模型的最合适阶次p，这时模型参数为｛ap（1），ap（2），…，ap（p），ρp｝，白噪声方差为σ2＝ρp。

将该参数和白噪声方差带入（3）式中，可得时域路面随机激励的AR模型xp（n）为：

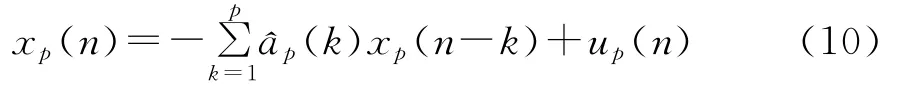
将得到的｛ap（1），ap（2），…，ap（p），ρp｝带入（5）式得到时域路面模型随机激励的p阶AR模型精确的功率谱密度估计值为：

2.3 双轴重型汽车路面随机激励AR模型

重型汽车以匀速v行驶在路面上，路面的随机激励以时间t为自变量。对于双轴汽车1／2车辆模型，在时域模型内，双轴重型汽车的前、后2个车轮处的路面激励存在如下关系：

根据傅里叶变换性质，（12）式可以转化为：

将（10）式得到的时域路面随机激励的AR模型xp（n）作为前轮的路面随机激励qf（n），然后根据（13）式中前、后轮之间的关系，可得后轮的路面随机激励qr（n）。

综上所述，可得1／2车辆模型的前、后轮路面随机激励向量的时域模型如下：

3 车辆振动模型的建立与动荷载的计算

行驶在不平整路面上车辆，受到路面的激励作用会产生大于车辆静载的动荷载，被认为是路面破坏的直接原因。本文采用1／2车辆模型对车辆动载对路面的永久变形损伤评价进行研究。

1／2车辆简化模型如图1所示。

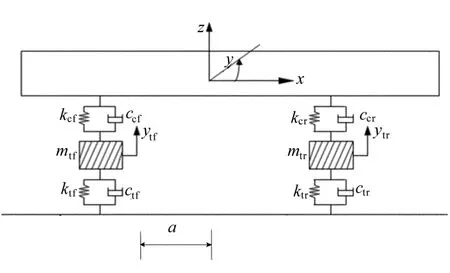
图1 1／2车辆简化模型

图1中，mtr为后轮质量；mtf为前轮质量；kcf为前悬挂系统刚度系数；ktf为前轮胎刚度系数；kcr为后悬挂系统刚度系数；ktr为后轮胎刚度系数；ccf为前悬挂系统的阻尼系数；ctf为前轮胎的阻尼系数；ccr为后悬挂系统的阻尼系数；ctr为后轮胎的阻尼系数；a为前轮中心至车架质心的距离。

当汽车在不平整路面上行驶时，前轮会受到路面随机激励qf（t）的作用，后轮会受到路面随机激励qr（t）的作用，导致前轮产生垂直位移z1（t），后轮产生垂直位移z2（t），车身产生垂直位移z3（t）和俯仰角位移z4（t）。

采用牛顿定律法建立车辆系统动力学微分方程，并根据拉格朗日方程可得车辆振动方程为：

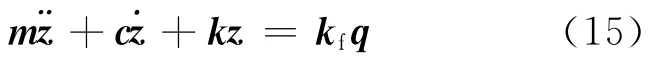
其中

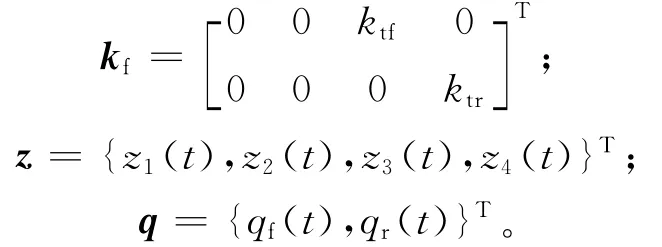
其中，z为位移向量；q为路面激励向量；m为质量矩阵；c为阻尼矩阵；k为刚度矩阵；kf为右端与路面激励对应的矩阵；m为车身质量；J为车架绕质心的转动惯量；b为后轮中心至车架质心的距离。

由（15）式可以求得双轴重车的车轮静载和车辆振动时对路面的动荷载，前轮静载Gf、后轮静载Gr、前轮动载Fdf、后轮动载Fdr分别为：

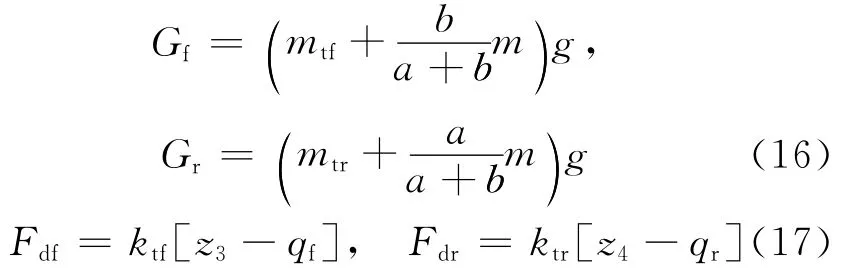
其中，g为重力加速度。

4 动载对路面永久变形损伤评价指标

在车辆对路面的损伤评价中，往往考虑的是静载，而忽略了由于路面不平度的激励产生的动载破坏。1958—1961年，AASHTO通过大量试验得出车辆对半刚性基层沥青路面的疲劳破坏与车辆的静态轴载的四次方成正比关系；1995年，Cole和Cebon在四次方的基础上指出，车辆轴载在空间上具有空间重复性，并基于这种空间重复性提出了95百分位四次方评价指标，来评价车辆对路面的疲劳破坏。

基于以上关系，并借鉴我国沥青路面设计规范和美国AASHTO2002中路面设计规范中的关于路面永久变形破坏理论，提出车辆对路面永久变形破坏指标为：

其中，Jp为永久变形破坏指数，Jp＞1时，Jp越大，说明车辆对路面永久变形损伤越严重；A1.8为车辆对路面的1.8次幂的力；σA1.8 为A1.8的标准差；mA1.8为A1.8的均值。

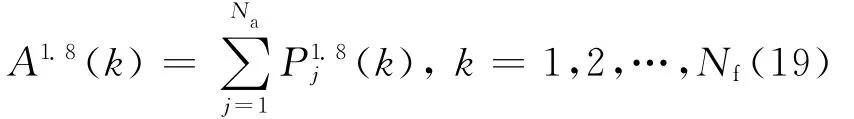
其中，Pj（k）为第j轴车轮对路面上第k点的作用力；Na为汽车总轴数；Nf为汽车经过路面各位置的总点数。

其中，SA1.8（f）为1.8次幂和力的功率谱密度；f1、f2为动态轮胎力频率的上下限，在实际中f1＝0.1Hz，f2＝50Hz；Fj为汽车静止时第j轴车轮对路面的作用力。

本文用车辆对路面永久变形破坏指数Jp来评价车辆动载对路面造成的永久变形破坏。在路面等级、车速v、动态轮胎力频率的下限f1和上限f2已知的情况下，确定总采样时间t、频率间隔Δf和采样频率fs，可以得到离散时间t（i）＝iΔt，i＝1，2，…，Ns。相应的各轮路面随机激励的时间序列为qf（n）、qr（n），n＝1，2，…，Ns。

汽车匀速行驶，考虑汽车经过路面时所有车轴对路面每个位置的累计破坏，可截取路面随机激励的一部分进行研究。在时间t内，双轴重型汽车前、后轴车轮经过路面同一位置的时差为：

因此，汽车匀速行驶时，双轴汽车前后轮在路面各位置上的随机激励时间序列可表示为：

其中，对应qf（k），k＝1，2，…，Nf；对应qr（k），k＝

通过车辆模型求得的车辆前、后轴对路面的作用力序列，利用Burg法可求得A1.8的AR时域模型xp（n），而后可得xp（n）的功率谱密度估计值为：

通过SA1.8（f）和双轴汽车静止时对路面的作用力可求得σA1.8和mA1.8，即可计算Jp。

5 算 例

给定动态轮胎力的频率上下限分别为0.1Hz和50Hz，总采样长度为1 000m，采样间隔Δt＝0.02s，采样频率fs为50Hz，国家给定的标准路面谱标准，见表1所列，采用该标准得到双轴重车前、后轮的路面随机激励时间序列q（k），并结合车辆振动模型，利用Matlab计算出A1.8的标准差σA1.8和A1.8的均值mA1.8，便可求出道路永久变形损伤指数Jp。根据路面随机激励AR模型的原理，在Matlab中开发相应的程序。双轴重车在速度为50km／h时，路面随机激励AR模型如图2所示。

表1 路面不平度8级分类标准

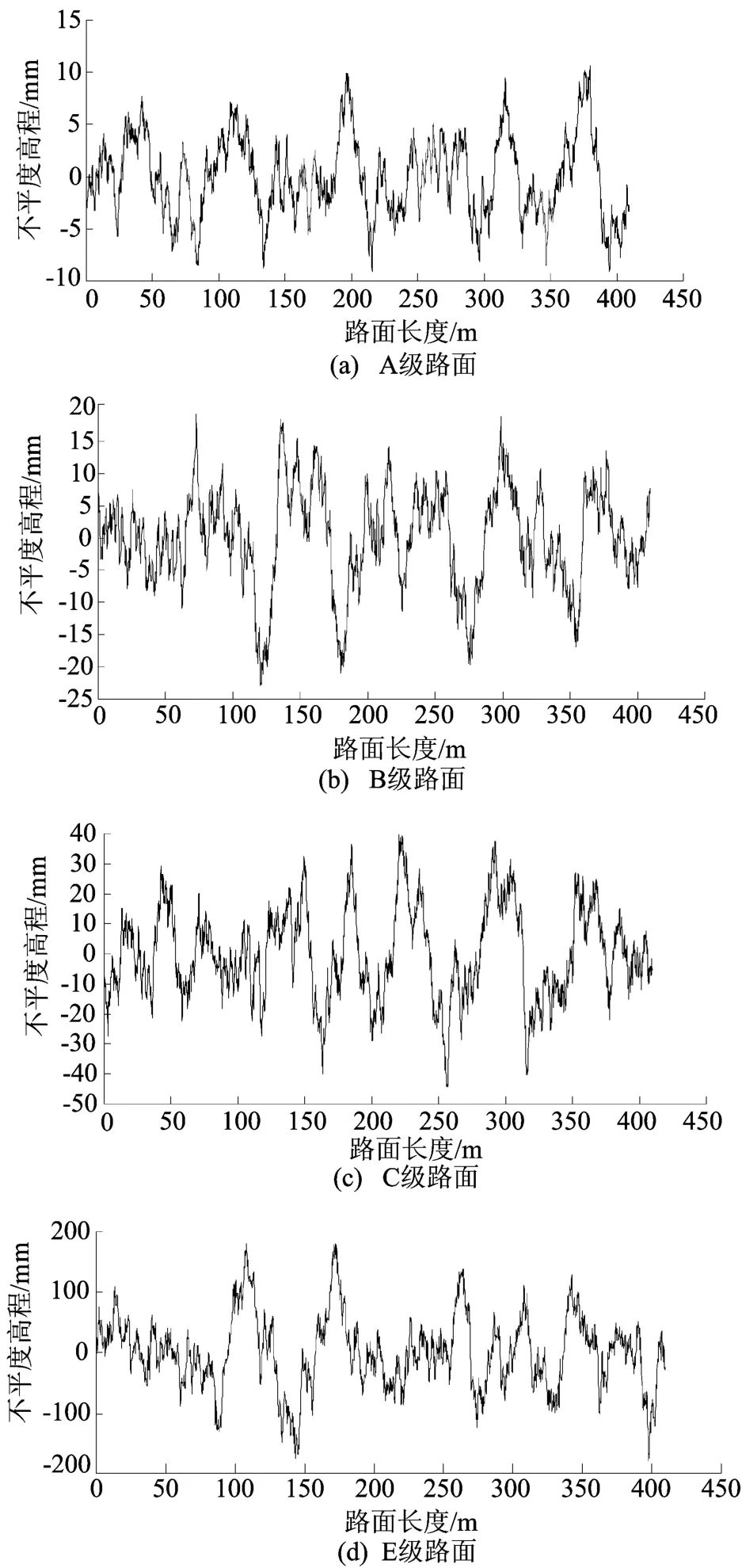
图2 车速50km／h时不同路面随机激励AR模型结果

双轴车辆在时速50km／h行驶在A、B、C、D 4种等级路面上时，车辆动载对路面永久变形损伤指数如图3所示。

从图3可以看出，路面不平度等级越差，车辆行驶时对路面的永久变形损伤越严重，因此，需要对路面进行及时养护，增大路面的平整度，以减小车辆动载对路面的永久变形损伤。

图3 不同路面等级永久变形损伤指数

在B级路面时，车辆分别以20、30、40、50、60、70、80km／h的速度行驶时，双轴重车车辆动载对路面永久变形损伤指数如图4所示。

图4 不同车速下永久变形损伤指数

从图4可以看出，随着车速的增加，车辆动载对路面永久变形损伤指数也在增加，即车辆动载对路面永久变形损伤在增大，因此，在路面不平度等级较差时应控制车速，以减小车辆动载对路面的永久变形损伤。

6 结束语

本文在时域模型内研究了双轴重型汽车对路面的永久变形损伤，利用AR模型得到了路面随机激励功率谱密度和车辆动载谱密度，得到了双轴重型汽车在时域模型下对路面的永久变形损伤指数，并且损伤指数随着路面不平度的增加而增大；在同一路面等级时，损伤指数随着车速的增加而增大。

本文所分析的车辆动载对路面的永久变形损伤只考虑了路面等级和车速的影响，因此有必要对其他因素的作用做进一步分析。且本文所采用的1／2车辆模型，与整车模型相比有较大差距，因此用整车模型评价车辆动载对沥青路面永久变形损伤将是下一阶段研究的重点。

［1］ 李 强，佘小红，邱延峻.沥青混凝土路面永久变形预测研究综述［J］.公路，2004（5）：1－5.

［2］ 何振亚.现代谱估计［M］.南京：东南大学出版社，1990：32－44.

［3］ 李 勇，徐 震.MATLAB辅助现代工程数字信号处理［M］.西安：西安电子科技大学出版社，2002：168－180.

［4］ 赵 旗，李 杰，崔乃栋.路面随机输入下军用汽车振动性能时域仿真［J］.中国科技论文，2012，7（11）：862－865，875.

［5］ 张永林，钟毅芳.车辆路面不平度输入的随机激励时域模型［J］.农业机械学报，2004，35（2）：9－12.

［6］ 彭 佳，何 杰，李旭宏，等.路面不平度随机激励时域模型的仿真比较与评价［J］.解放军理工大学学报：自然科学版，2009，10（1）：77－82.

［7］ 薛念文，赵伟燕，陈 龙，等.基于AR模型对路面不平度的时域模拟［J］.拖拉机与农用运输车，2008，35（2）：87－88，93.

［8］ 朱茂桃，刘 建，王国林.路面不平度重构的AR模型阶数确定方法研究［J］.公路交通科技，2010，27（7）：25－28，51.

［9］ 吕彭民，尤晋敏，和丽梅.路面随机不平度下车辆对路面的动载特性［J］.交通运输工程学报，2007，7（6）：55－58，69.

［10］ 任卫群，张云清，金国栋.动态轮胎力仿真的新方法［J］.系统仿真学报，2003，15（5）：628－630.

［11］ 任卫群，张云清，金国栋.公路车辆对道路破坏性研究的系统化方法［J］.中国公路学报，2005，18（4）：110－114.

［12］ Sweatman P F.A study of dynamic wheel forces in axle group suspensions of heavy vehicles，Australian Road Research Board Special Report［R］.ARRB Group Limited，1983.

［13］ Eisenmann J.Dynamic wheel load fluctuations：road stress［J］.Strasse und Autobahn，1975，4（2）：127－128.

［14］ Cole D J，Cebon D.Assessing the road－damaging potential of heavy vehicles［J］.Proceedings of the Institution of Mechanical Engineers，Part D：Journal of Automobile Engineering，1991，205：223.

［15］ 刘大维，陈焕明，刘 伟，等.基于整车多体模型的重型车辆对路面的损伤评价［J］.振动与冲击，2010，29（4）：92－96.

［16］ 张洪信，陈秉聪，张铁柱.车辆对路面损伤的全概率评价［J］.青岛大学学报，2002，17（1）：60－63.

［17］ GB 7301－86，车辆振动输入：路面平度表示方法［S］.