液力变矩器机构变量交互作用研究

王安麟,孟庆华,李文嘉,韩继斌



液力变矩器机构变量交互作用研究

王安麟1,孟庆华1,李文嘉1,韩继斌2

液力变矩器以良好的自适应性、低速稳定性等优越性被广泛应用于车辆和工程机械。提高液力变矩器性能一直是学者研究的重要课题,而改进液力变矩器机构参数是提高性能的主要措施。

Ejiri等对液力变矩器的扁平化进行了研究并取得了一定的成果[1-2]。雷雨龙等研究了液力变矩器叶片的成型方法,并对叶型设计方法进行了改进,以有效指导液力变矩器叶栅系统的设计[3-4]。Wu等借助一体化平台对液力变矩器叶栅系统进行了设计、分析[5]。韩克非等基于正交试验法研究了泵轮叶片角对液力变矩器性能的影响,并对泵轮叶片角进行了优化[6]。范春顺基于三维流体仿真分析了叶片数对液力变矩器性能的影响[7]。刘城等研究了叶片数对液力变矩器性能影响的显著性,并对叶片数进行了优化,以提高液力变矩器的综合性能[8]。

综上,对提升液力变矩器性能的研究多为叶型的改进、叶片角的优化及叶片数的优化。液力变矩器属于复杂的流固耦合机构,而机构变量间的交互作用对液力变矩器性能存在影响。现有的对叶片角与叶片数的优化设计采用的分步优化方法割裂了叶片角与叶片数的耦合关系,无法考虑叶片角与叶片数的交互作用。本文运用正交试验法合理安排试验,通过三维全流道仿真得到样本数据,就液力变矩器性能对机构变量的灵敏度进行了分析,着重研究了叶片角与叶片数的交互作用对液力变矩器性能的影响,综合叶片角与叶片数建立了响应曲面模型,采用多目标遗传算法进行了优化。

1 三维流体仿真

1.1 三维流体仿真参数设定

液力变矩器属于流道封闭的复杂流固耦合机构,随着计算流体动力学(CFD)的迅速发展,采用CFD模拟液力变矩器内部流场的真实流动情况日渐成熟[9]。

本文采用全流道模型进行了仿真,以提高CFD仿真的准确度。液力变矩器流道模型网格划分如图1所示。不同叶轮间相对运动的数值解析方法主要有混合界面法、冻结转子法和滑移网格法,对于向心式涡轮液力变矩器采用冻结转子法较为适合[10]。通过文献参考及仿真经验,压力速度耦合算法可采用SIMPLE算法,空间离散格式为一阶上游迎风格式,湍流模型为RNGk-ε湍流模型[11]。

图1 流道模型网格

1.2 三维流体仿真验证

为验证CFD三维仿真结果的准确性,通过台架试验获得试验数据,将试验数据与CFD三维仿真结果进行对比。如图2所示,在不同传动比i下,变矩比K和泵轮扭矩系数λB的相对误差均小于3%,效率η的绝对误差小于5%,表明CFD三维仿真结果精度较高,可以用于研究机构变量对液力变矩器性能的影响。

图2 CFD仿真与试验性能参数对比

2 液力变矩器性能对机构变量的灵敏度分析

2.1 机构变量选择

液力变矩器的机构变量包括叶片角、叶片数、叶片形状和叶片厚度等。传统液力变矩器优化设计过程中普遍认为,叶片进、出口角度对液力变矩器性能影响最为显著[12],忽略了叶片数的影响,而且现有研究均未考虑叶片角与叶片数的交互作用对液力变矩器性能的影响。本文综合叶片角与叶片数对液力变矩器性能影响进行了灵敏度分析,以泵轮作为研究对象,将泵轮入口角βB1、出口角βB2和叶片数nB及与泵轮有直接影响的涡轮入口角βW1和导轮出口角βD2作为变量进行了研究,而涡轮出口角βW2、导轮入口角βD1、涡轮叶片数nW和导轮叶片数nD不作为变量。液力变矩器原始模型的机构变量参数如表1所示。

2.2 正交试验设计

试验设计中对试验指标有影响的变量称为因子,把因子变化的各种状态称为因子水平。正交试验设计是研究多因子、多水平试验的一种高效、快速、经济的试验设计方法[13]。本文液力变矩器的正交试验设计因子有βB1、βB2、nB、βW1和βD2,每个因子取4个水平(水平1～水平4),水平的选取主要参考现有液力变矩器的设计范围[14],如表2所示。由此,选用正交表L32(49)安排试验。

表1 液力变矩器原始模型的机构变量参数

表2 液力变矩器性能影响因子水平表

液力变矩器工作性能的评价主要有变矩性能、经济性能和能容性能,本文研究的性能指标分别是起动变矩比K0、最高效率ηm和最高效率工况下泵轮扭矩系数λBm。根据选用的正交表建模、仿真得到样本数据。

2.3 灵敏度分析

灵敏度分析是研究一个模型的输出响应对输入因子变化的敏感程度的方法。本文通过灵敏度分析确定各因子对液力变矩器性能指标的影响程度,主要包括线性相关程度、二次相关程度和因子间交互作用程度,并通过帕累托(Pareto)图来表征。图中横坐标的贡献率反映因子对性能指标影响程度的百分比,正值表示正效应,负值表示反效应。对于不同性能指标,贡献率排在前10位的因子作用程度如图3所示。

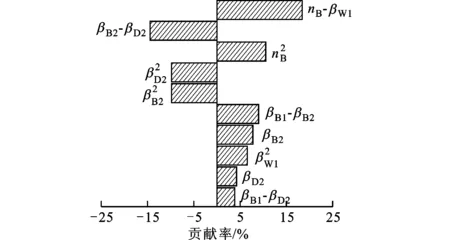
(a)起动变矩比

(b)最高效率

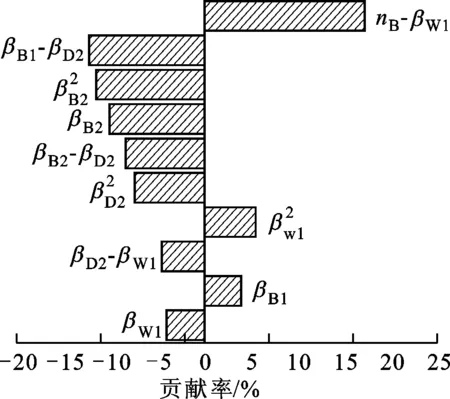
(c)最高效率工况下扭矩系数图3 各性能指标的Pareto图

交互效应图反映了2个因子间的交互作用对性能指标的影响程度和关系,其绘制方式是在一个因子取不同水平的情况下,将另一因子对响应的主效应图进行叠加而成。通过方差分析可以得到交互效应图,如果图中2条线不平行或交叉,则表示存在交互作用,交互作用的强弱由不平行程度反映;如果图中2条线相互平行,则表示不存在交互作用。起动转矩比、最高效率和最高效率工况下扭矩系数的各叶片角与泵轮叶片数交互效应图如图4～图6所示。

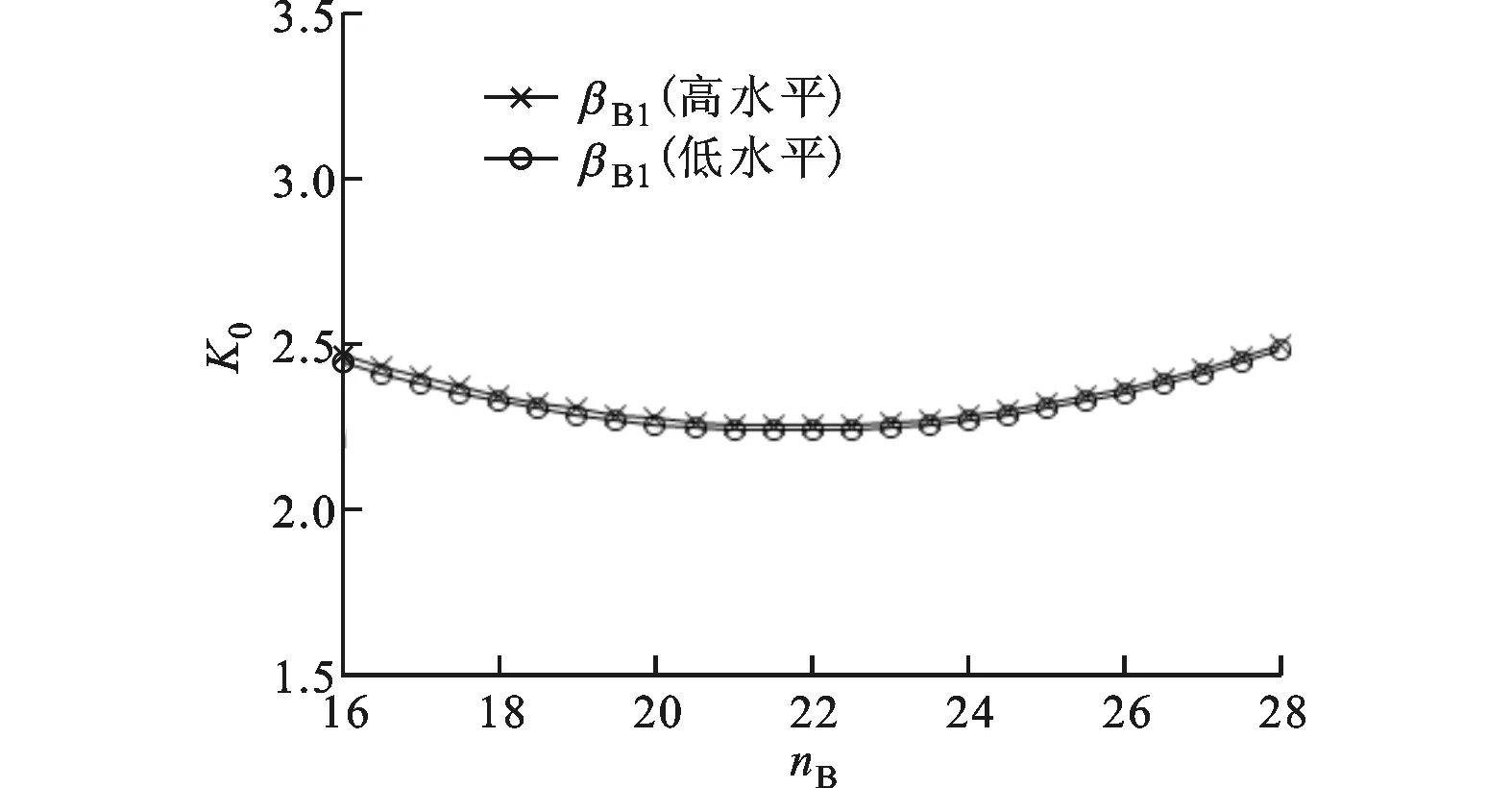
(a)泵轮入口角与泵轮叶片数

(b)泵轮出口角与泵轮叶片数

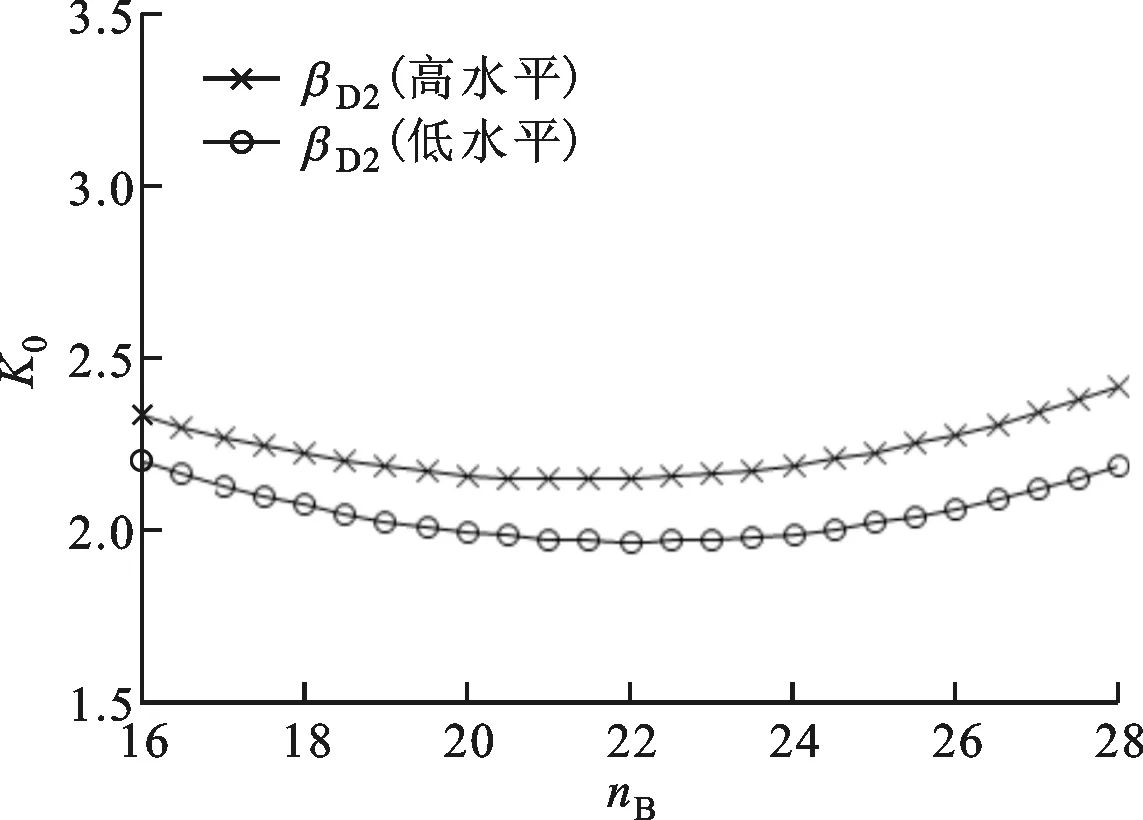
(c)导轮出口角与泵轮叶片数

(d)涡轮入口角与泵轮叶片数图4 起动变矩比的交互效应图

(a)泵轮入口角与泵轮叶片数

(b)泵轮出口角与泵轮叶片数

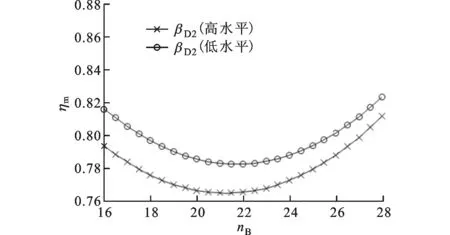
(c)导轮出口角与泵轮叶片数

(d)涡轮入口角与泵轮叶片数图5 最高效率的交互效应图

(a)泵轮入口角与泵轮叶片数

(b)泵轮出口角与泵轮叶片数

(c)导轮出口角与泵轮叶片数

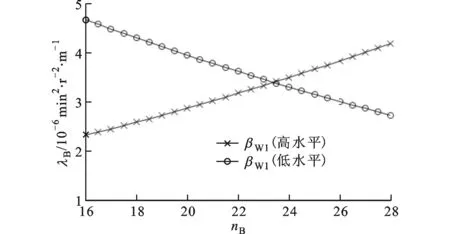
(d)涡轮入口角与泵轮叶片数图6 扭矩系数的交互效应图

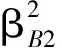
综上可知,泵轮叶片数与涡轮入口角的交互作用对液力变矩器性能的影响相当显著。其原因是工作介质是从泵轮出口流向涡轮入口,而叶片数的改变会使液流偏离发生改变,从而对涡轮入口的冲击损失产生较大影响,而涡轮入口角的改变直接影响涡轮入口处的冲击损失,从而说明泵轮叶片数与涡轮入口角之间存在着较强的耦合关系。由上述分析还可知,相对于叶片角,叶片数对液力变矩器性能也存在显著影响,说明传统优化设计中认为叶片角对液力变矩器性能影响最为显著而低估叶片数的影响是不合理的。

3 基于响应曲面法的机构变量综合优化方法

响应曲面法(RSM)是依据样本数据建立因子与响应的多元回归方程以便进行优化的方法。基于响应曲面法的优化流程如图7所示。样本数据由机构变量参数(因子的水平)和实际响应(性能指标)组成,根据样本数据和响应曲面模型形式可拟合响应曲面各项系数。响应曲面存在拟合误差,如果该误差满足要求,则说明响应曲面模型可以进行优化,然后基于响应曲面模型采用遗传算法寻优,将优化结果通过CFD三维仿真进行验证;如果误差不满足要求,则修改响应曲面模型形式,以保证拟合精度。

图7 基于响应曲面法的优化流程图

3.1 响应曲面模型

响应曲面模型是采用多元回归方程建立的因子与响应之间的函数关系。本文采用五元三次回归方程构造响应曲面,其形式为

根据正交试验仿真得到的样本数据拟合五元三次回归方程的系数。响应曲面模型的拟合误差和拟合度R2如表3所示。

表3 响应曲面法拟合误差分析

由表3可知,响应曲面模型的拟合误差较小,拟合度均在0.9以上,说明利用正交试验设计所得的样本数据对三次响应曲面拟合精度较高,进而说明可以基于响应曲面法对液力变矩器进行优化。

3.2 机构变量综合优化方法

由于响应曲面模型具有非线性性,为避免传统优化方法陷入局部极值点,采用遗传算法对响应曲面进行了优化。本文中液力变矩器性能指标有3个,其优化属于多目标优化问题,故采用多目标遗传算法进行优化[15]。

为比较叶片角与叶片数综合优化和分步优化对液力变矩器性能的提升程度,将泵轮入口角、泵轮出口角、导轮出口角和涡轮入口角作为变量,采用与2.2节相同的水平取值和正交表安排试验来获取仿真样本数据,通过响应曲面模型优化得到最优叶片角组合,然后单独对泵轮叶片数进行优化。将分步优化结果和综合优化结果通过CFD三维仿真进行了验证。基于不同优化方法得到的机构变量参数与性能指标的对比如表4所示。

由表4可知,综合优化方法相比于分步优化方法的起动变矩比提高了0.336,最高效率提高了2.1%,最高效率工况下泵轮扭矩系数提高了0.306×10-6min2·r-2·m-1,各项性能指标均有不同程度的提高,进一步说明了叶片角与叶片数的交互作用对液力变矩器性能影响较为显著。

表4 基于不同优化方法得到的机构变量参数与性能指标的对比

4 结 论

(1)在对比试验数据确认三维流体仿真的基础上,采用正交试验法科学、合理地安排试验,通过全流道流体仿真得到液力变矩器性能指标,即起动变矩比、最高效率和最高效率工况下泵轮扭矩系数,从而保证了研究结果的可靠性。

(2)以泵轮作为研究对象,分析了液力变矩器性能对机构变量的灵敏度,重点研究了机构变量间的交互作用对液力变矩器性能影响的显著性,研究表明:泵轮叶片数对液力变矩器性能的影响较为突出,其显著性要高于某些叶片角;涡轮入口角与泵轮叶片数的交互作用对液力变矩器的性能指标均有较为显著影响。

(3)运用响应曲面法建立了具有较高逼近精度的五元三次响应曲面模型。基于所建响应曲面模型,采用多目标遗传算法进行了优化,并对比了不考虑叶片角与叶片数交互作用的分步优化结果,从而验证了叶片角与叶片数综合优化方法可以提升液力变矩器的性能,进一步说明了机构变量间的交互作用对液力变矩器性能具有显著影响。

[1] EJIRI E, KUBO M. Influence of the flatness ratio of an automotive torque converter on hydrodynamic performance [J]. ASME Journal of Fluids Engineering, 1999, 121(3): 614-620.

[2] KIM G, JANG J. Effects of stator shapes on hydraulic performances of an automotive torque converter with a squashed torus [C]∥SAE 2002 World Congress. Washington, DC, USA: SAE, 2002: 155-160.

[3] 雷雨龙, 王健, 胡廷辉, 等. 液力变矩器叶栅动量矩分配规律 [J]. 吉林大学学报: 工学版, 2009, 39(4): 880-884. LEI Longyu, WANG Jian, HU Tinghui, et al. Angular of momentum distribution on blades of hydraulic torque converter [J]. Journal of Jilin University: Engineering and Technology Edition, 2009, 39(4): 880-884.

[4] 王立军, 吴光强, 王欢. 基于叶片角变化规律的液力变矩器改型设计法 [J]. 同济大学学报: 自然科学版, 2011, 39(11): 1673-1679. WANG Lijun, WU Guangqiang, WANG Huan. Design strategy for modification of torque converters based on variation law of blade angle [J]. Journal of Tongji University: Natural Science Edition, 2011, 39(11): 1673-1679.

[5] WU Guangqiang, YAN Peng. System for torque converter design and analysis based on CAD/CFD integrated platform [J]. Chinese Journal of Mechanical Engineering: English Edition, 2008, 21(4): 35-39.

[6] 韩克非, 吴光强, 王立军. 基于正交设计的泵轮叶栅关键参数对液力变矩器的性能影响优化分析 [J]. 中国电机工程学报, 2010, 30(35): 65-70. HAN Kefei, WU Guangqiang, WANG Lijun. Performance optimization analysis of the effects of pump cascade key parameters on torque converter based on orthogonal design [J]. Proceedings of the CSEE, 2010, 30(35): 65-70.

[7] 范春顺. 液力变矩器叶片数对其性能影响的研究 [D]. 长春: 吉林大学, 2007.

[8] 刘城, 潘鑫, 闫清东, 等. 基于DOE及RSM的液力变矩器叶片数对性能的影响及优化 [J]. 北京理工大学学报, 2012, 32(7): 689-693. LIU Cheng, PAN Xin, YAN Qingdong, et al. Effect of blade number on performance of torque converter and its optimization based on DOE and response surface methodology [J]. Transactions of Beijing Institute of Technology, 2012, 32(7): 689-693.

[9] 方杰, 齐迎春, 马文星, 等. 液力变矩器流场的数值模拟与分析 [J]. 同济大学学报: 工学版, 2005, 33(5): 673-677. FANG Jie, QI Yingchun, MA Wenxing, et al. Simulation and analysis of flow field in hydrodynamic torque converter [J]. Journal of Tongji University: Natural Science Edition, 2005, 33(5): 673-677.

[10]JUNG J H, KANG S, HUR N. A numerical study of a torque converter with various methods for the accuracy improvement of performance prediction [J]. Progress in Computational Fluid Dynamics, 2011, 11(3): 261-268.

[11]刘春宝, 马文星, 朱喜林. 液力变矩器三维瞬态流场计算 [J]. 机械工程学报, 2010, 46(14): 161-166. LIU Chunbao, MA Wenxing, ZHU Xilin. 3D transient calculation of internal flow field for hydrodynamic torque converter [J]. Chinese Journal of Mechanical Engineering, 2010, 46(14): 161-166.

[12]马文星. 液力传动与设计 [M]. 北京: 化学工业出版社, 2004: 182-184.

[13]田中玄一. 实验设计法概论 [M]. 北京: 兵器工业出版社, 1990: 9-12.

[14]朱经昌. 液力变矩器的设计与计算 [M]. 北京: 国防工业出版社, 1991: 74-75.

[15]YADAV O P, RATHOD V, RATHORE A, et al. Optimizing reliability-based robust design model using multi-objective genetic algorithm [J]. Computers & Industrial Engineering, 2013, 66(2): 301-310.

[本刊相关文献链接]

王安麟,孟庆华,曹岩,等.液力变矩器的叶片数神经网络模型.2015,49(7):11-16.[doi:10.7652/xjtuxb201507003]

李大海,李天石.非均匀采样系统的支持向量回归建模与控制.2011,45(3):65-69.[doi:10.7652/xjtuxb201103012]

宫武旗,伍儒康.求解流线曲率法反命题的一种新型有限差分方法.2015,49(3):11-13.[doi:10.7652/xjtuxb201503002]

燕浩,刘梅清,梁兴,等.大型轴流泵空化特性的数值模拟.2014,48(11):44-50.[doi:10.7652/xjtuxb201411008]

张明宇,王永生,靳栓宝,等.喷水推进泵压力脉动特性数值计算及分析.2014,48(11):51-57.[doi:10.7652/xjtuxb2014 11009]

李学臣,席光.离心叶轮出口流动分离区影响因素的数值研究.2013,47(9):16-22.[doi:10.7652/xjtuxb201309003]

(编辑 苗凌)

(1.同济大学机械与能源工程学院,201804,上海;2.山推工程机械股份有限公司,272073,山东济宁)

为解决现有液力变矩器机构变量优化设计中采用分步优化方法存在的问题,通过对比台架试验数据确认了三维流体仿真结果的准确性,运用正交试验、通过全流道流体仿真得到了起动变矩比、最高效率和最高效率工况下泵轮扭矩系数;采用方差分析法研究了机构变量间的交互作用对液力变矩器性能影响的显著性,在考虑交互作用的基础上建立了五元三次响应曲面模型且应用多目标遗传算法进行了优化。研究表明:机构变量间交互作用显著影响着液力变矩器的性能,采用机构变量综合优化方法优化后,起动变矩比提高了0.336,最高效率提高了2.1%,最高效率工况下泵轮扭矩系数提高了0.306×10-6min2·r-2·m-1。

液力变矩器;机构变量;交互作用;显著性;响应曲面模型

Study on Mechanism Variables Interaction of Torque Converter

WANG Anlin1,MENG Qinghua1,LI Wenjia1,HAN Jibin2

(1. School of Mechanical Engineering, Tongji University, Shanghai 201804, China;2. Shantui Construction Machinery Co., Ltd., Jining, Shandong 272073, China)

In order to solve the problem caused by the separated step optimization for the design of the mechanism variables of torque converter, the significance of mechanism variables interaction was studied. Firstly, the accuracy of three dimensional fluid simulation results was confirmed in comparison with the bench test data. Secondly, starting torque ratio, highest efficiency and pump wheel torque coefficient at the transmission ratio of highest efficiency were obtained through full flow passages simulation based on the orthogonal experiments, and the significance of mechanism variables interaction was discussed through analysis of variance. Finally, the ternary quintic response surface model was established and optimized by using multi-objective genetic algorithm. The experiment results showed that mechanism variables interaction significantly affected torque converter performance and after optimization using the integrated optimization method of mechanism variables, starting torque ratio increased by 0.336, highest efficiency increased by 2.1%, and pump wheel torque coefficient at the transmission ratio of highest efficiency increased by 0.306×10-6min2·r-2·m-1.

torque converter; mechanism variables; interaction; significance; response surface model

2014-12-23。 作者简介:王安麟(1954—),男,教授,博士生导师。 基金项目:2012年国家重大科技成果转化资助项目(〔2012〕258号)。

时间:2015-06-17

http:∥www.cnki.net/kcms/detail/61.1069.T.20150617.0902.008.html

10.7652/xjtuxb201509001

TH137.332

A

0253-987X(2015)09-0001-07