固定翼电磁数据双分量联合电导率深度成像

朱凯光，李冰冰，王凌群，谢 宾，王 琦，程宇奇

吉林大学仪器科学与电气工程学院，长春 130026



固定翼电磁数据双分量联合电导率深度成像

朱凯光，李冰冰，王凌群，谢 宾，王 琦，程宇奇

吉林大学仪器科学与电气工程学院，长春 130026

传统固定翼航空电磁探测采用总场dB/dt进行电导率深度成像，不仅损失多分量测量信息，dB/dt与电导率的非唯一性也影响数据的成像精度。笔者提出了一种基于磁场双分量(Bx,Bz)查表的联合电导率深度成像算法，根据固定翼电磁响应的正演计算，建立按时间道划分的Bx-Bz-电导率-飞行高度数据表，利用磁场双分量联合查表与插值算法确定视电导率，避免了由于电磁数据二值性引起的视导率不确定性问题；根据扩散深度公式得到视深度，并计算成像深度，从而得到双分量联合电导率深度成像结果。基于一维大地模型正演数据与准二维大地模型正演加噪数据，分别采用磁场双分量联合查表法、总场查表法和单分量查表法对仿真数据进行电导率深度成像，结果表明磁场双分量联合查表法优于单分量与总场查表法，较单分量电导率深成像精度提高了7%。

固定翼航空电磁；磁场双分量查表法；联合电导率深度成像；扩散深度

0 引言

固定翼航空电磁探测系统以固定翼飞机为载体，采用偶极-偶极收发装置，发射线圈安置于飞机周围，接收线圈由电缆线拖拽悬挂于飞机下方，可测量三分量电磁响应，具有勘探效率高、探测深度大、勘探面积广等优势，广泛应用于地质勘查中[1-3]。固定翼航空电磁数据量庞大，反演解释耗时费力，一般采用电导率深度成像 ( conductivity-depth imaging，CDI) 技术快速处理海量航空电磁数据，得到地下电导率分布图，从而确定地下异常分布[4-5]。

目前国内外航空电磁探测的电导率深度成像方法很多，如Liu等[6]提出了基于薄板模型的成像方法，其视电导率及视深度由最小二乘迭代法导出；Wolfgram等[7]采用解卷积算法将任意波形的电磁响应转换为阶跃响应，通过τ域分解，得到地下电导率分布；Huang等[8]提出了基于假层-半空间查表的电导率深度成像方法，引入电导率为0的假想层代表人文圈；朱凯光等[9]利用神经网络获得更为准确的视电导率；陈小红等[10]采用改进后的一阶、二阶电导率深度成像算法，提高了对地层电导率的灵敏性；毛立峰[11]建立了σ-β数据表查询视电导率，消除了电磁响应的二值性。

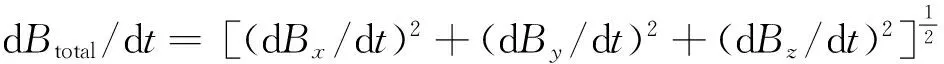
笔者根据磁场对导电异常体探测与单调性的优势[16]提出了一种基于B场响应的双分量联合电导率深度成像算法。该算法基于固定翼时间域航空电磁正演理论，采用层状大地模型，推导出固定翼航空电磁系统x与z分量的B场响应，建立水平分量磁场(即Bx)-垂直分量磁场(即Bz)-电导率-飞行高度数据表，给出双分量Bx-Bz联合查表算法，最后通过理论仿真验证双分量查表法联合电导率深度成像算法的有效性。

1 正演算法

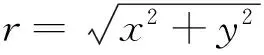
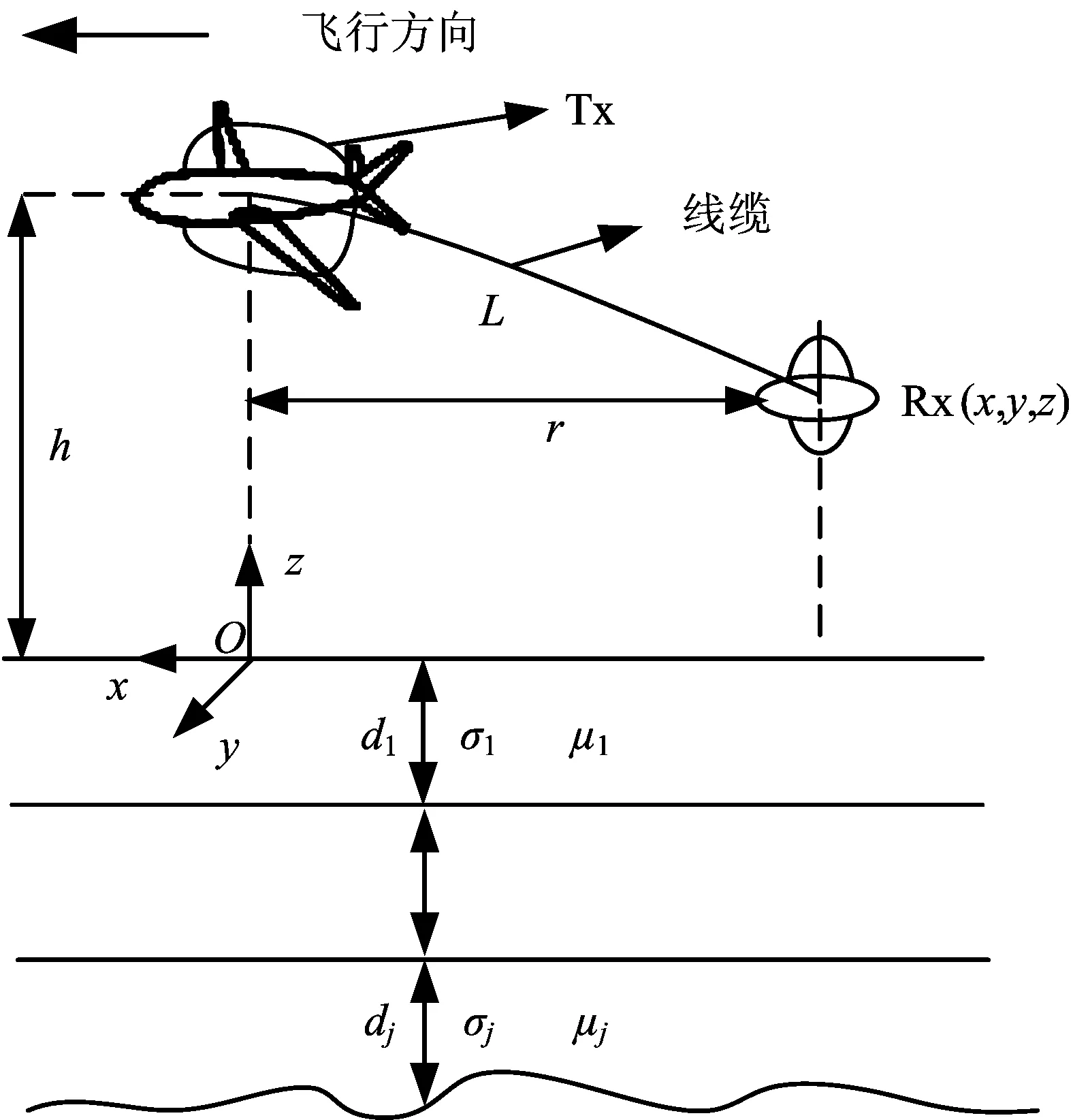
图1 固定翼时间域航空电磁系统坐标系Fig.1 Coordinate of the fixed-wing time-domain electromagnetic system

根据电磁计算理论[17]，接收线圈处的二次场频率域水平分量磁场响应Bx(w)和垂直分量磁场响应Bz(w)的表达式分别为

(1)

(2)

其中：J0和J1分别为零阶和一阶贝塞尔函数；w为角频率；λ为积分变量；μ0为空气中的磁导率，μ0=4×10-7π H/m；反射系数rTE为

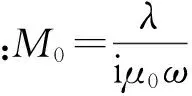
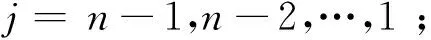
其中:μj=μ0。分别将式(1)、式(2)变换到s(复频率)域中，并除以s得到x分量和z分量的磁场瞬态响应表达式：

(3)

(4)

分别对式(3)、(4)做拉氏逆变换(L-1)得到系统双分量B场响应，作为电导率深度成像的数据表来源：

(5)

(6)

式中，零阶和一阶贝塞尔函数的无限积分(汉克尔变换)利用数值滤波算法(Guptasarma120点和140点)[18-19]计算。

2 Bx-Bz分量查表法联合电导率深度成像

2.1 电磁响应样本集的建立

设定固定翼航空电磁探测系统保持平稳飞行状态，飞行高度 在80～180 m等间隔选取101个，半空间模型的电导率在0.001～20.000 s/m按等对数间隔选取55个，形成101×55组半空间探测模型。利用上述正演算法，计算14个时间道(0.01～10.00 ms)各模型对应的双分量B场响应。按时间道划分，建立14个Bx-Bz-电导率-飞行高度数据表，表中任一点为由对应飞行高度及半空间模型确定的x和z分量B场响应，记为(Bx,Bz,σ,h)。图2给出了第k(1≤k≤14)道的部分Bx-Bz-电导率-飞行高度数据表示意图，其中电导率σ1<σ2<σ3，飞行高度h1>h2>h3>h4>h5>h6>h7>h8>h9。

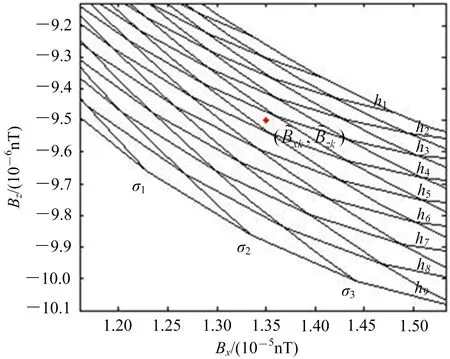
xk和zk为实际飞行测量的第k道x和z分量的B场响应。图2 第k道Bx-Bz-电导率-飞行高度数据表示意图Fig.2 Diagram of Bx-Bz-conductivity-altitude for channel k

2.2Bx-Bz分量联合查表算法

传统的总场查表法与单分量查表法电导率深度成像[20-22]采用总场响应或单分量响应进行匹配搜索查询视电导率，在搜索过程中需要提供实际的飞行高度以选择所需的数据表，而实际飞行探测过程中很难获取准确的飞行高度，给电导率的查询带来一定困难。

Bx-Bz分量联合查表法建立了Bx-Bz-电导率-飞行高度数据表，将飞行高度引入数据表中，在无法准确提供高度信息时不但可以快速获得视电导率，还可以得到对应的高度信息。同时采用x和z两个分量的电磁响应进行匹配搜索，不但增加了搜索时的约束条件，而且综合利用了x和z两个分量电磁响应的特性，从而提高成像的精确度。总场查表虽然也综合利用了多分量的响应，但对于两组不同的Bx、By和Bz分量，只要满足

就会得到相同的电导率查询结果。因此，总场查表虽然利用了多个分量，但由于进行了二对一的转换，损失了多分量测量信息。

(7)

(8)

其中：q1--q4为线段长度。

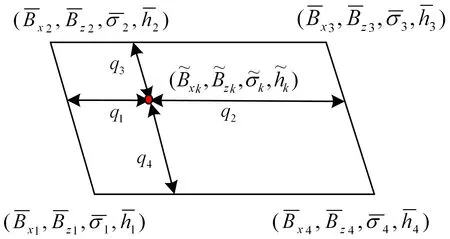
图3 插值算法示意图Fig.3 Diagram of interpolation algorithm

利用扩散深度公式计算得到第k个时间道对应的视深度dk：

式中，tk为第k个时间道对应的时间。在相邻2个时间道深度变化的基础上定义成像深度，即第k个时间道的成像深度是由上一时间道的成像深度加上利用趋肤深度公式计算得到的相邻两个时间道深度变化值的绝对值，从而获得第k个时间道对应的成像深度Dk[11]：

(9)

综上，Bx-Bz分量查表法联合电导率深度成像的步骤如下：

1)利用正演算法，建立Bx-Bz-电导率-飞行高度数据表表格；

2)通过磁场双分量联合查表与插值算法，确定视电导率；

3)利用扩散深度公式得到视深度，并计算成像深度，最终导出双分量联合电导率深度成像结果。

3 仿真结果

3.1 一维大地模型的电导率深度成像结果

设定固定翼航空电磁系统的z分量发射线圈高度为h=120 m，三分量接收线圈位于(-70,0,70) m处，系统参数同前。针对不同层状大地模型对Bx-Bz分量联合查表法、总场查表法与单分量查表法CDI进行对比研究。

以三层大地模型为例，选取了K型、H型典型地电模型作为参考模型对算法进行对比分析。表1为K、H型大地模型参数。

表1 K、H型大地模型参数表

Table 1 Parameter table of K and H style of geoelectric models

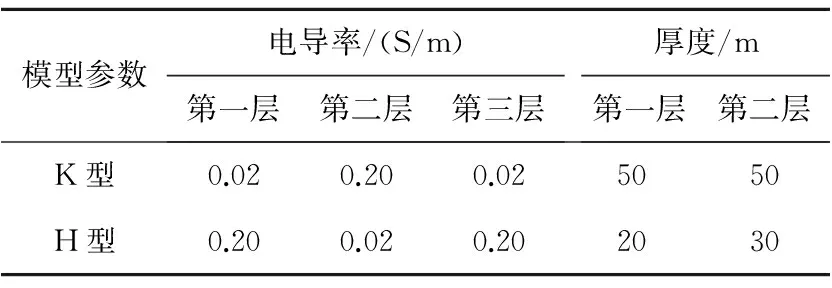
模型参数电导率/(S/m)第一层第二层第三层厚度/m第一层第二层K型0.020.200.025050H型0.200.020.202030

图4给出了K、H型两种三层大地模型采用Bx-Bz分量联合查表法、总场查表法与单分量查表法的CDI结果。可以看到，总场查表法成像结果与Bx和Bz单分量的查表结果一致，大致给出了三层大地模型的变化趋势，而Bx-Bz分量联合查表算法对K型大地模型(图4a)中间高导层的电导率和深度的成像结果与理论模型接近，即使H型大地的高阻层(图4b)，Bx-Bz分量联合查表算法也获得了优于总场与单分量查表法的成像结果。而由于查表算法是利用半空间大地模型的电磁响应作为数据表，而观测响应是含有异常体的三维大地模型;因此，利用观测值在半空间模型表中查询时，可能会出现部分点不在数据表中，使得成像结果不太光滑。

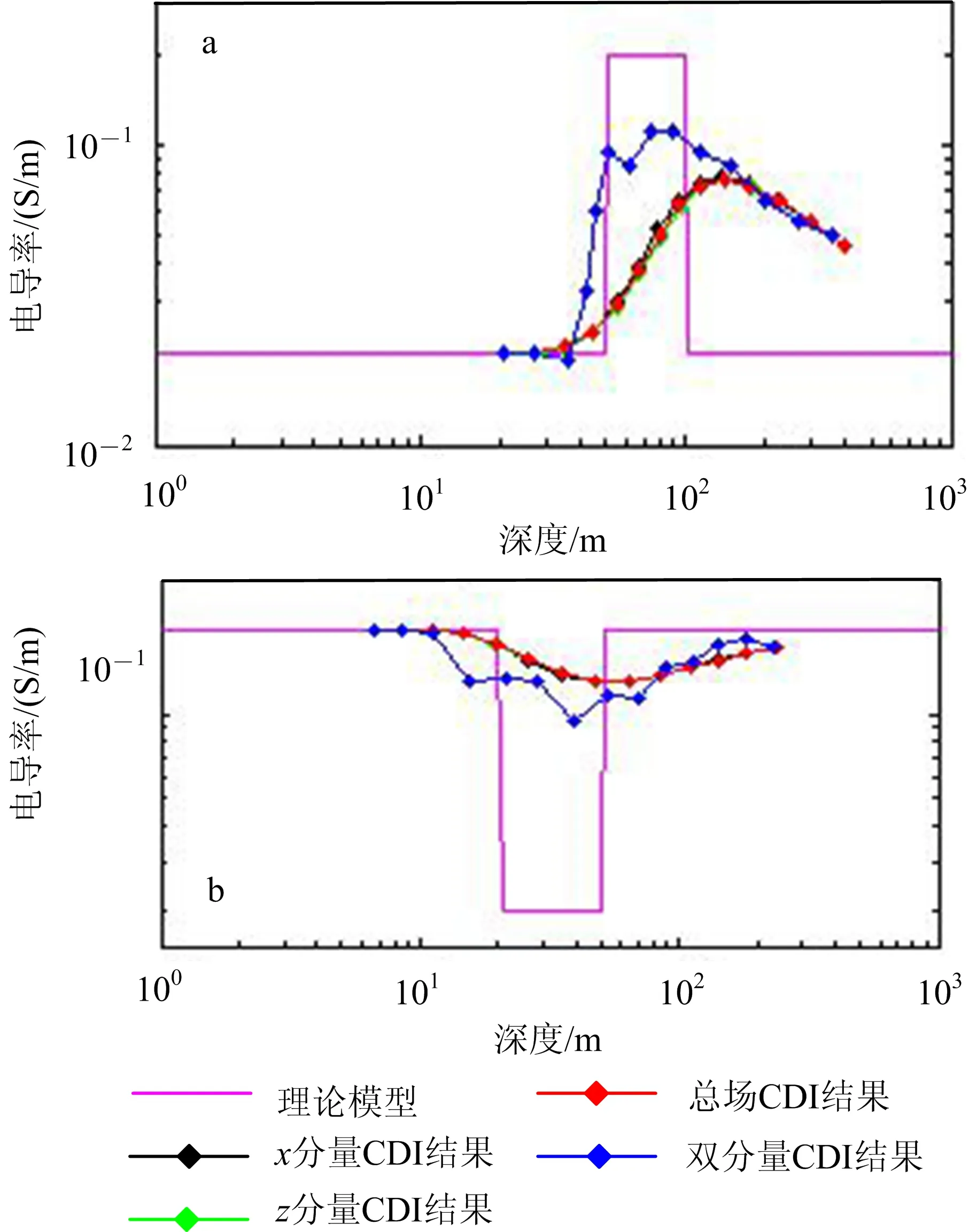
a．K型地电模型；b．H型地电模型。图4 三层典型大地模型CDI结果Fig.4 Results of four CDI methods on three-layer models

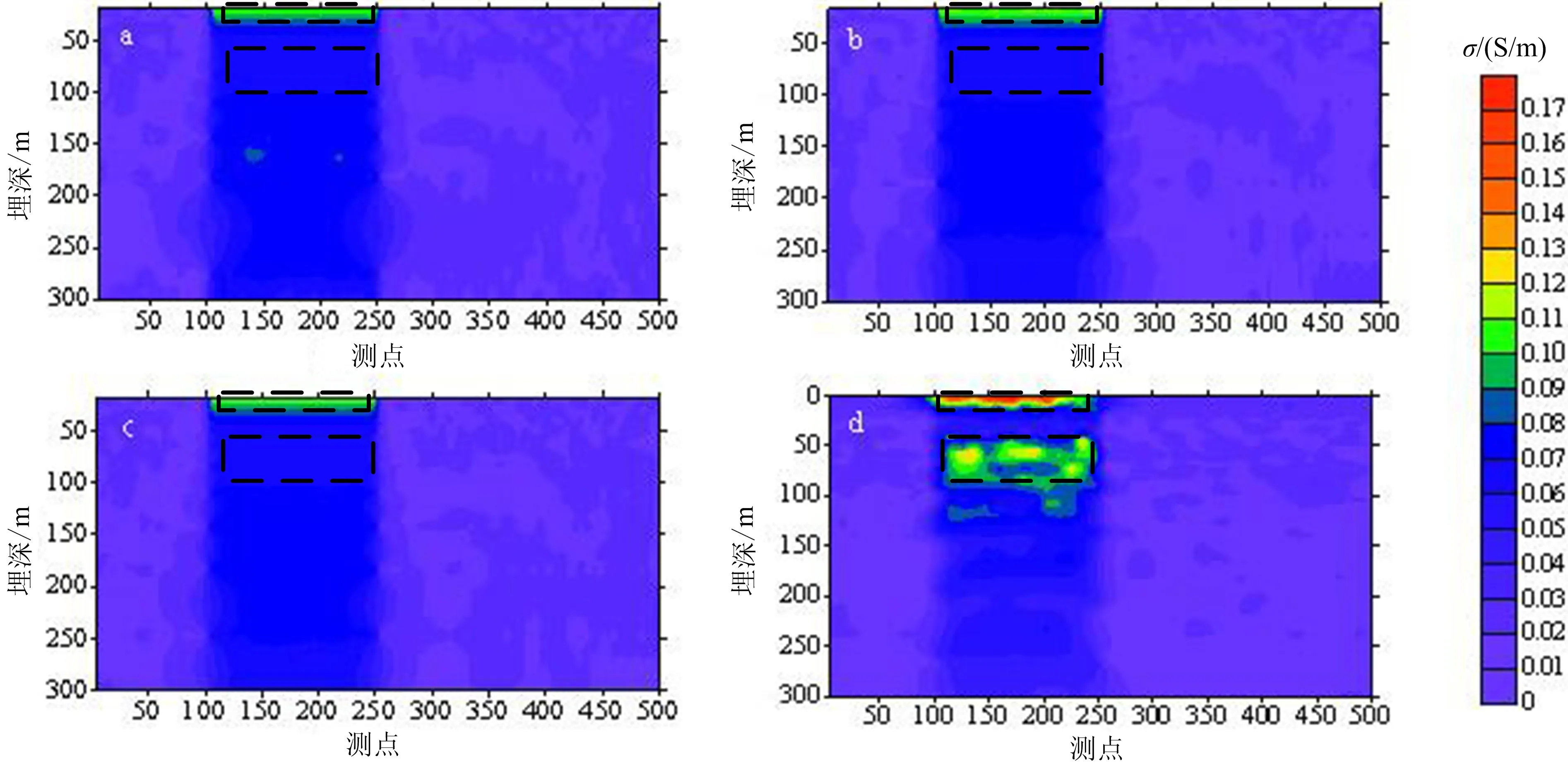
a.Bx分量查表法;b. Bz分量查表法;c. 总场响应查表法;d. Bx-Bz联合查表法。图6 四种方法的电导率深度成像结果对比图Fig.6 Results of four CDI methods on Pseudo-2D model

综上，总场查表法虽然利用了Bx和Bz两个分量进行电导率深度成像，但是由于进行了二对一的转换，仅获得了与单分量查表法近似的成像结果，损失了多分量测量获取地下信息的能力。而Bx-Bz分量联合查表算法充分利用Bx和Bz两个分量的信息，进行联合查表，获得了与真实大地模型更为接近的地下信息，提高了成像精度。

3.2 准二维大地模型的电导率深度成像结果

为评价Bx-Bz分量查表法联合电导率深度成像算法在实际中的应用，仿真构建了准二维大地模型，由500个5层大地模型相互连接构成。如图5所示，在测点100～250处的地下埋深2 m有一个厚度为5 m、电导率为0.2 s/m的异常，同时在埋深57 m处有一个厚度40 m、电导率0.2 s/m的异常，周围基岩的电导率为0.02 s/m。对上述大地模型进行正演计算获得其电磁响应剖面数据，并加入均方根相对误差为5%的白噪声，仿真野外实测数据。

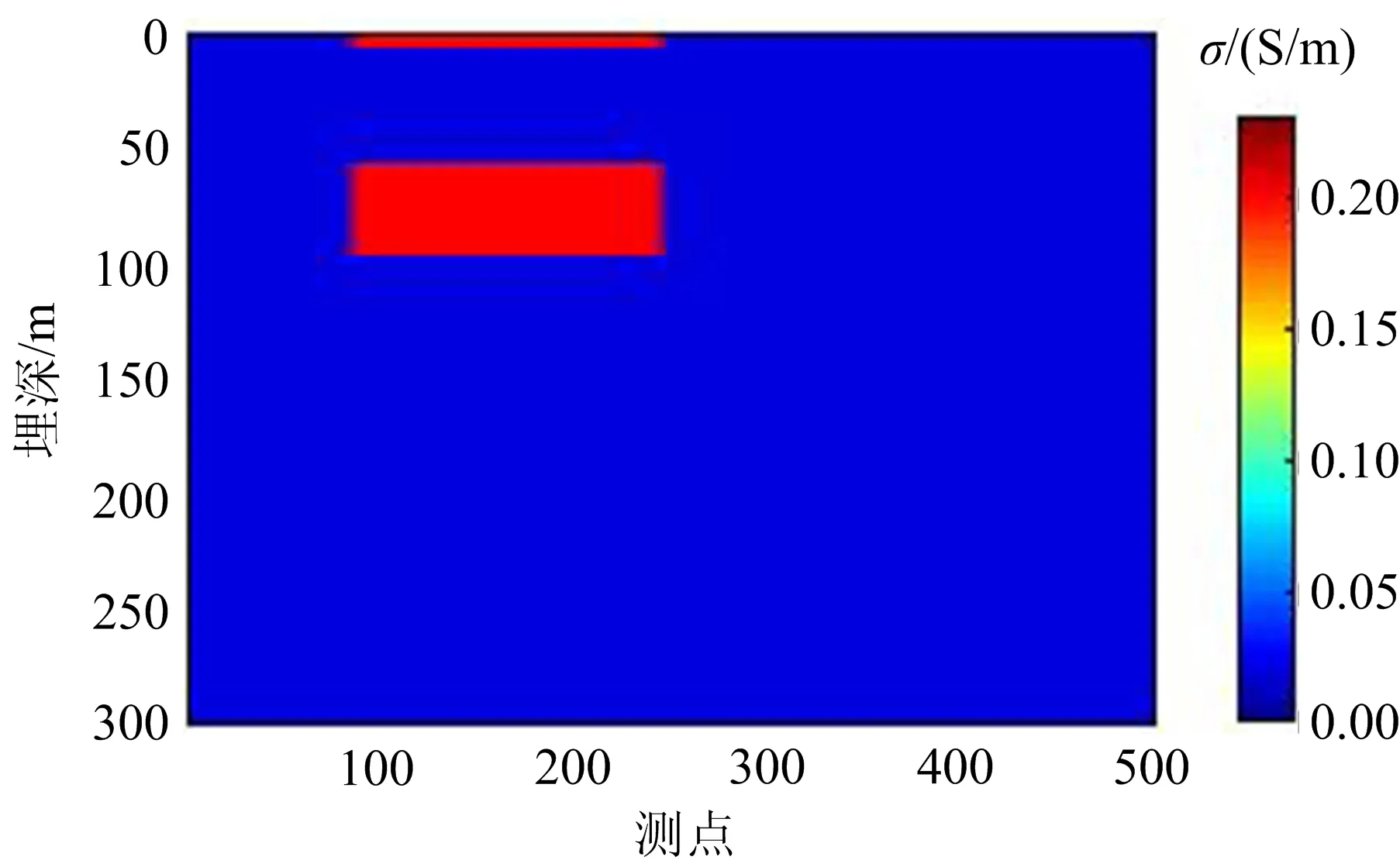
图5 理论大地模型Fig.5 Pseudo-2D theoretical model

为进一步对比成像效果，分别采用Bx分量查表法、Bz分量查表法、总场响应查表法及Bx-Bz分量联合查表法对数据进行电导率深度成像。图6分别展示了上述四种方法对于含噪准二维数据的CDI结果。

可以看到，Bx分量查表法(图6a)、Bz分量查表法(图6b)与总场查表法(图6c)的准二维含噪数据的CDI结果都较好地反映了埋深2 m的导电异常体，屏蔽了其下埋深57 m处的导电异常体，而图6d给出的Bx-Bz分量联合CDI结果却较为清晰地揭示了导电薄层下的低阻异常体，与理论模型一致。笔者计算了测点175处电导率深度成像结果的相对误差平均值得知，Bx分量查表、Bz分量查表、总场查表法以及Bx-Bz分量联合查表法的相对误差分别为22.07%、21.65%、21.84%、14.72%，即本文研究算法的成像精度较单分量电导率深度成像提高了7%左右。

4 结论

1)本文研究的基于磁场双分量的联合电导率深度成像算法，充分利用了多分量电磁探测数据，取得了优于总场与单分量查表法的成像结果。

2)一维大地模型的仿真结果表明该算法提高了对导电薄层的识别能力；准二维大地模型加噪数据的成像结果进一步证明在低阻覆盖层存在的情况下，联合电导率深度成像算法能够增强对其下导电异常体的识别能力，综合成像精度较单分量电导率深度成像提高了7%左右，为固定翼航空瞬变电磁资料解释提供了新思路。

吉林大学地球信息探测仪器教育部重点实验室航空电磁组的全体成员对此文进行了帮助和指导，在此表示衷心的感谢！

[1] Fountain D. Airborne Electromagnetic Systems:50 Years of Development[J]. Exploration Geophysics, 1998, 29(2): 1-11.

[2] Annan A P.Effect of Differential Transmitter/Receiver Motion on Airborne Transient EM Interpretation[J]. Geophysics, 1999, 49(1): 670-670.

[3] 胡平, 李文杰, 李军峰, 等.固定翼时间域航空电磁勘查系统研发进展[J]. 地球学报,2012, 33(1): 7-12. Hu Ping, Li Wenjie, Li Junfeng, et al. The Advances in the Development of Fixed-Wing Airborne Time-Domain Electromagnetic System[J]. Acta Geoscientica Sinica, 2012, 33(1): 7-12.

[4] Macnae J C, Smith R, Polzer B D, et al. Conductivity-Depth Imaging of Airborne Electromagnetic Step-Response Data[J]. Geophysics, 1991, 56(1): 102-114.

[5] 嵇艳鞠, 冯雪, 于明媚, 等.基于多元线性回归的HTEM三维异常体电导率-深度识别[J]. 吉林大学学报：地球科学版，2014, 44(5), 1687-1694. Ji Yanju, Feng Xue, Yu Mingmei, et al. Conductivity-Depth Identification of HTEM 3D Anomalies Based on Multiple Linear Regression[J]. Journal of Jilin University: Earth Science Edition, 2014, 44(5), 1687-1694.

[6] Liu G, Asten M. Conductance-Depth Imaging of Airborne TEM data[J]. Exploration Geophysics,1994, 24(4): 655-662.

[7] Wolfgram P, Karlik G. Conductivity-Depth Transform of GEOTEM Data[J]. Exploration Geophysics, 1995, 26(2/3): 179-185.

[8] Huang H, Rudd J. Conductivity-Depth Imaging of Helicopter-Borne TEM Data Based on a Pseudolayer Half-Space Model[J]. Geophysics, 2008,73(3): 115-120.

[9] 朱凯光, 林君, 韩悦慧, 等.基于神经网络的时间域直升机电磁数据电导率深度成像[J]. 地球物理学报，2010, 53(3): 743-750. Zhu Kaiguang, Lin Jun, Han Yuehui, et al. Research on Conductivity Depth Imaging of Time Domain Helicopter-Borne Electromagnetic Data Based on Neural Network[J]. Chinese Journal of Geophysics, 2010, 53(3): 743-750.

[10] 陈小红, 段奶军.时间域航空电磁快速成像研究[J]. 地球物理学进展, 2012,27(5): 2123-2127. Chen Xiaohong, Duan Naijun. Study on Fast Imaging of Airborne Time-Domain Electromagnetic Data[J]. Progress in Geophys., 2012, 27(5): 2123-2127.

[11] 毛立峰.中心回线式直升机TEM资料的电导率-深度成像方法[J]. CT 理论与应用研究, 2013,22(3): 429-437. Mao Lifeng. Conductivity-Depth Imaging Algorithm for Central-Loop Helicopter TEM[J]. CT Theory and Applications, 2013, 22(3): 429-437.

[12] Smith R S, Keating P B. The Usefulness of Multicomponent, Time-Domain Airborne Electromagnetic Measurements[J]. Geophysics, 1996, 61(1): 74-81.

[13] 席振铢, 刘剑, 龙霞, 等.瞬变电磁法三分量测量方法研究[J]. 中南大学学报：自然科学版，2010,41(1):272-276. Xi Zhenzhu, Liu Jian, Long Xia, et al.Three-Component Measurement in Transient Electromagnetic Method[J]. Journal of Central South University: Science and Technology, 2010, 41(1): 272-276.

[14] 张莹莹.水平电偶源地空系统瞬变电磁法多分量解释技术及全域视电阻率定义研究[D]. 西安: 长安大学，2013. Zhang Yingying. Study on Multi-Component Interpretation and Full Field Apparat Resistivity Definition of Semi-Airborne Transient Electromagnetic Method with Electric Dipole on the Surface[D]. Xi’an: Chang’an University, 2013.

[15] 王琦, 林君, 于生宝, 等. 固定翼航空电磁系统的线圈姿态及吊舱摆动影响研究与校正[J]. 地球物理学报，2013，56(11)：3741-3750. Wang Qi, Lin Jun, Yu Shengbao, et al. Study on Influence and Correction of Coil Attitude and Bird Swing for Fixed-Wing Time-Domain Electromagnetic System[J]. Chinese Journal of Geophysics, 2013, 56(11)：3741-3750.

[16] Huang H. Locating Good Conductors by Using the B-Field Integrated From Partial dB/dtWaveforms of Time-Domain EM Systems[C]. SEG/San Antonio Annual Meeting. San Antonio: SEG, 2007: 688-692.

[17] Wait J R. Geo-Electromagnetism[M]. [S.l.]: Academic Press Inc,1982.

[18] Guptasarma D, Singh B. New Digital Linear Filters for Hankel J0and J1Transforms[J]. Geophysical Prospecting, 1997, 45(5): 745-762.

[19] Guptasarma D, Singh B. Computation of the Time-Domain Response of a Polarizable Ground[J]. Geophysics, 1982, 47(11): 953-963.

[20] Wolfgram P, Karlik G. Conductivity-Depth Transform of GEOTEM Data[J].Exploration Geophysics, 1995, 26(3): 179-185.

[21] Vrbancich J, Fullagar P K, Macnae J. Bathymetry and Seafloor Mapping via One Dimensional Inversion and Conductivity Depth Imaging of AEM[J]. Exploration Geophysics, 2000,31(4): 603-610.

[22] 马铭遥.时间域航空电磁数据全波成像与处理技术研究[D]. 长春: 吉林大学,2013. Ma Mingyao. Study on Full-Waveform Imaging and Processing of Time-Domain Airborne Electromagnetic Data[D]. Changchun: Jilin University, 2013.

Conductivity-Depth Imaging of Fixed-Wing Airborne Electromagnetic Data

Zhu Kaiguang，Li Bingbing，Wang Lingqun，Xie Bin，Wang Qi，Cheng Yuqi

CollegeofInstrumentationandElectricalEngineering,JilinUniversity，Changchun130026，China

The traditional fixed-wing airborne electromagnetic survey lost multi-component measurement information for the reason of using the total field as the data base for the conductivity depth imaging. The imaging precision is decreased due to the non-uniqueness of the dB/dt. A joint conductivity depth imaging approach based on the lookup method of two-componentBfield response is proposed. Based on the fixed-wing electromagnetic forward calculation, this paper establishes a table ofBx-Bz-conductivity-altitude, usesBfield to avoid the uncertainty of conductivity due to the binary value of electromagnetic data, uses the joint lookup method of two-componentBfield and interpolation algorithm to determine the conductivity, and then takes the advantage of the diffusion depth formula to obtain the depth, and finally to process the joint conductivity depth imaging. Compared to the total field and simple component lookup method applied in the one-dimensional and quasi-two-dimensional forward simulation, the CDI of two-componentBfield gets more ideal fitting effects; and the imaging precision is improved by 7%.

fixed-wing airborne electromagnetic；lookup method of two-component magnetic field；joint conductivity-depth imaging；diffusion depth

10.13278/j.cnki.jjuese.201506301.

2015-02-08

国家自然科学基金项目(41274076)；国家高技术研究发展计划项目(2013AA063904)；国家重大科研装备研制项目(ZDYZ2012-1-03)

朱凯光(1970--)，女，教授，主要从事地球物理电磁探测及随机信号处理研究，E-mail:zhukaiguang@jlu.edu.cn。

10.13278/j.cnki.jjuese.201506301

P631.3

A

朱凯光，李冰冰，王凌群，等. 固定翼电磁数据双分量联合电导率深度成像.吉林大学学报:地球科学版,2015,45(6):1839-1845.

Zhu Kaiguang，Li Bingbing，Wang Lingqun, et al. Conductivity-Depth Imaging of Fixed-Wing Airborne Electromagnetic Data.Journal of Jilin University:Earth Science Edition,2015,45(6):1839-1845.doi:10.13278/j.cnki.jjuese.201506301.