一种可存储路径的三维非均质空间最短距离场生成算法

2015-03-06王丽芳吴湘滨张宝一李小丽

吉林大学学报（地球科学版） 2015年4期

王丽芳，吴湘滨，张宝一,2，李小丽，杨莉

1.中南大学有色金属成矿预测与地质环境监测教育部重点实验室/地球科学与信息物理学院,长沙 410083 2.中国地质大学地质过程与矿产资源国家重点实验室，武汉 430074

王丽芳1，吴湘滨1，张宝一1,2，李小丽1，杨莉1

针对成矿定量预测强调三维空间信息综合研究的特殊需求和地质要素定量表达难、深层次信息挖掘难等关键问题，笔者提出了一种基于三维非均质地质空间的最短距离场算法，并且可回溯出目标体元到源体元的最短路径。应用该方法实现了对某铜矿区三维地质实体模型深层次和组合信息的挖掘，在反映断层对地质空间分划作用的基础上，建立了侵入岩体的最短距离场，可用于对侵入岩体热力场和围岩蚀变等问题的分析。

距离场；三维；非均质；路径；成矿预测

0 引言

随着现代成矿理论的发展、强穿透物化探技术的革新和地质勘查程度的深入，二维空间地质信息表达方式的局限性愈来愈明显，需要从真三维空间角度来分析和解决矿产资源定量预测问题，发展综合地质数据的深层次三维空间分析手段，从而提升对矿化空间分布规律性的认识来指导找矿，解决隐伏找矿工作中直接指示信息少、干扰大、三维展布复杂、数据挖掘难等问题。近年来，三维地质建模已成为三维地理信息系统(3D GIS)、地球科学、三维计算机图形学等各相关领域的研究热点和前缘，一大批三维地质建模软件在地质、石油、采矿等行业得到推广使用，如GoCAD、Lynx、Surpac、Landmark、Mincom、EarthVision、Vulcan、Micromine、Datamine等。所谓三维地质建模，即采用适当的数据结构在计算机中建立起能反映地质构造形态和各要素之间关系，以及地质体物理、化学属性空间分布等地质特征的数学模型。Houlding[1]最早阐述了地下三维可视化技术的核心理论和基本方法，Lynx软件系统就是基于该理论和方法体系实现的；Mallet[2]也提出了一种新的地质目标计算机辅助设计方法以适应地质、地球物理和油藏工程的需要，其理论和方法体系已经成为GoCAD 软件系统的主要技术支撑；武强等[3]提出了一种“逐步优化”(stepwise refinement)的多源数据整合三维地质建模方法，来渐进、有效地提高三维模型的精度；吴立新等[4]将三维地质建模的应用分为三维可视化、三维查询、三维分析、工程应用4个目标层次；潘懋等[5]概括了三维地质建模“多源数据-多方法集成-多层次干预”的“三多”建模思路。三维地质建模是将不同专业、期次、来源、类型的数据在统一环境下进行集成，建设多源地学数据仓库的有效途径，为后续三维可视化的数值分析提供了数据和技术支撑[6-7]，可以在工程勘察[8]、矿产勘查[9-10]和地下水调查[11]等领域开展更深入的研究。

建立起囊括地层、构造、物化探等要素的区域三维地质空间数据模型是开展三维地学模拟的前提条件[11]。三维地质空间数据模型可以分为基于实体的模型和基于场的模型两类[12-13]：前者将三维地质空间表示为离散的点、线、面、体四类几何实体的组合，侧重于表达地质构造形态和各要素之间的关系，也称为三维几何模型；后者则将三维地学空间剖分为规则的或不规则的体元(voxel)构成的连续场，侧重于表达三维地质空间内物理、化学属性的空间分布特征，也称为三维属性模型。三维地质建模的位势场方法(potential-field method)就采用了协同克里格方法将地质接触面的位置数据和构造场的产状数据插值成一个连续的三维位势场标量函数来表达地质实体的几何形状，将地质接触位置集合作为等值面的参考点，而产状数据为标量函数的梯度，将断层表示为位势场中的不连续[14-16]。在进行三维空间分析时，由于场数据便于空间叠加、空间相关和空间模拟等空间分析，因而通常使用三维场数据进行三维空间分析和工程应用。

三维栅格(3D-raster)模型是一种有代表性的规则数据场表示方法，它是一种无采样约束的面向场物质(如重力场、磁场、矿化品位)的连续空间标准分割方法，一般用八叉树(octree)模型对其进行数据压缩及空间索引[17]，广泛应用于资源、水体、污染和环境等问题的建模。三维栅格地质模型可以看作为一幅含有空间目标(如地质体、构造、矿体等)的三维图像，这幅三维图像中不仅有空间目标的分布范围，还可利用GIS三维空间分析方法对其进行深加工，从而衍生新的数据场来开展统计分析。

在地质研究中，经常需要对地表或地下的某些地质体(如断层、岩体等)进行距离分析，因而距离场的提取及其形态特征的表达对于众多地质问题的解决具有特殊的意义。例如，在研究地下成矿元素运移时，一个重要的问题就是分析成矿元素运移到达的空间区域，这就需要考虑最短距离和运移路径。Payne和Toga[18]提出了一个从完整的封闭表面来计算距离场的算法，并检验了距离场在表面移动、内插和缝合中的应用；李芳玉[19]在Dijkstra算法与距离变换的基础上，提出了一种基于三维栅格的最短距离算法，并将其应用于非均质的三维缓冲体的生成；李莹等[20]以立方体品位模型为基础，提出了一种按同级品位提取三维矿体轮廓的算法，从三维的角度分析矿体品位分布的不均匀性；陈建平等[21]以Micromine软件为平台建立了新疆阿勒泰地区可可托海3号伟晶岩脉9个共生结构带的三维实体模型和钻孔三维品位模型，并利用钻孔数据开展隐伏矿体的定位和储量估算；安聪荣等[22]提出了一种可应用于非均质三维地质空间中、允许存在多个源点的栅格模型最短距离等值面算法；毛先成等[23]以安徽铜陵凤凰山矿田为例，采用8个模板进行三维欧氏距离变换生成了栅格欧氏距离场，并利用开闭滤波或闭开滤波的数学形态学分析提取了地质体表面的形态趋势。

三维距离分析常用于构建三维地质变量，是矿体与控矿要素间关联关系提取及成矿三维定量预测模型建立的基础。毛先成等[24-25]分别以广西大厂锡矿和安徽铜陵凤凰山矿田为例，按照“地质数据集成--成矿信息定量提取--立体定量预测”的流程，从场分析的观点建立控矿地质因素的场模型以及矿化分布场模型，制作统计数据散点图得到控矿地质因素与矿化指标的关联关系，建立了反映这种关联关系的矿体立体定量预测模型；张宝一等[10]以辽宁红透山铜矿为例，建立了成矿信息场、地层形态场、断裂影响场、地球物理场等多源地学空间数据场，并提取了三维定量预测的地质控矿指标集和建立了预测模型。

为了满足成矿定量预测强调三维空间信息综合研究的特殊需求，解决地质要素定量表达难、深层次信息挖掘难等关键问题，笔者提出了一种基于三维非均质地质空间的最短距离场算法，其可回溯出目标体元到源体元的最短路径；应用该方法建立了某铜矿区侵入岩体的最短距离场，可用于对侵入岩体的热力场和围岩蚀变等问题的分析，场的非均质性可反映出断层对热力场的分划作用。

1 三维地质空间场的建立

以面向成矿预测应用为例，利用矿区构造或矿体的总体趋势来确定体元的三轴方向u、v、w(默认分别与坐标轴x、y、z平行)，每个体元i用其在3个轴向上的序号组合(ui,vi,wi)来唯一标识，三维地质空间场定义为按规则格网阵列记录的三维数组。三维地质空间场的结构特征(如格网起始点、分辨率及方向等)直接影响着地质空间数据场的构建和空间相关场的计算精度。按照一定体元大小(格网分辨率)对所描述的地质对象进行重建时，格网分辨率直接确定了数据量和计算精度，一般通过计算矿化品位各方向的变差函数，根据变程值、矿体形态及误差范围综合确定格网分辨率。

笔者使用SURPAC软件建立了某铜矿区地质体三维实体模型(图1a)，该模型是仅以不规则三角网(TIN)面表示的空间闭合实体。在进行地质控矿指标、矿化分布指标提取时，按照单元尺寸为10 m×10 m×10 m的体元将建模范围内的三维地质空间剖分为规则场，并结合矿区的数字高程模型(DEM)剔除地表以上的体元(见附录A1)，如图1b所示。三维地质空间场涵盖了从矿山收集到的地质、物化探、勘探资料的三维空间范围，统一的三维空间场结构便于地、物、化、遥等各专业信息的综合分析。

2 三维地质空间场的赋值

三维地质空间场的结构确定以后，首要任务就是结合三维地质实体模型，对三维场体元进行多源地学信息属性赋值，主要包括：将三维地质实体模型转换为体元模型，这一过程可看作是对地质体的三维栅格化，图2a和图2b分别为将三维侵入岩体和断层体元实体模型作为约束条件进行栅格化得到的体元模型；将三维地质实体模型转换为三维位势场的标量场，整合及假整合地层界面表示为等值面，断层及其他不整合面作为不连续面；利用勘探工程(槽、井、坑、钻)采样数据进行重采样和空间插值(如地质统计学方法、距离反比加权法等)，对三维地质空间场开展主要成矿元素的属性估值，对三维物化、钻井化探等数据进行场属性赋值，其他二维物、化探及遥感数据只进行地表体元赋值。接下来需设计三维最短距离场算法，计算非均质地质空间中任意体元相对于多个“地质源实体”的最短距离，将地质源实体(如断裂、侵入岩体等)的影响也表示为标量场。

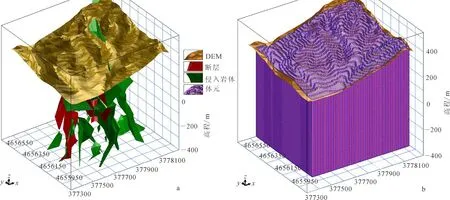
图1 某铜矿区三维地质实体模型(a)与三维地质空间场(b)Fig.1 3D geological entity model (a) and 3D geological spatial field (b) of a copper deposit area

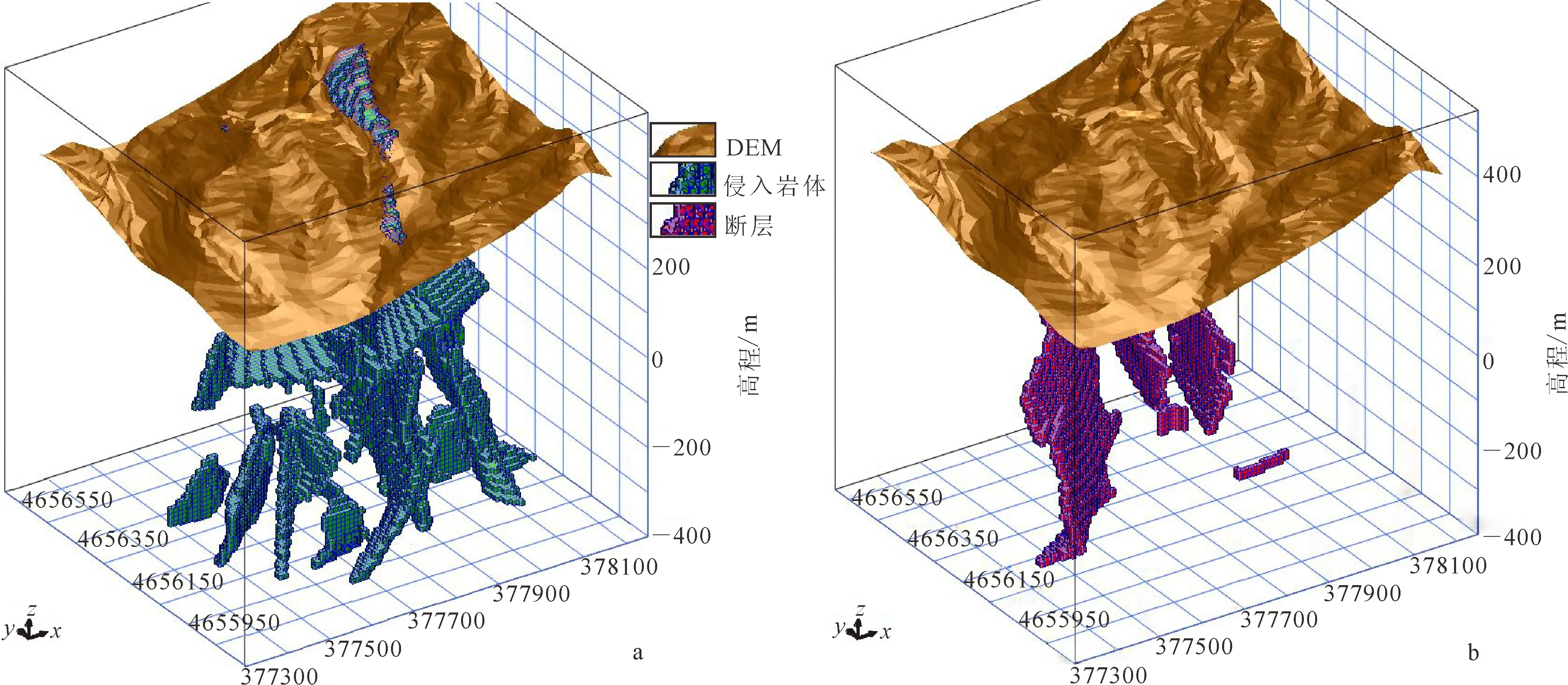
a.侵入岩体；b.断层。图2 某铜矿区三维地质体元模型Fig. 2 3D geological voxel model of a copper deposit area

3 加权最短距离场的生成算法

3.1 最短距离场的定义

最短距离场可表示为每个体元k到含有m个“源实体”(可以是地质界面或感兴趣区域)的集合S中所有实体的距离中的最小值的集合：

(1)

式中：Fd为最短距离场的场值；d(,)为距离计算函数。

定义出发点所在的体元为源体元，目标点所在的体元为目标体元，它们处在同一格网中。距离量算就是要计算目标体元与源体元的距离。设体元的大小为1单元，任意两个体元之间的距离可以有多种定义方式，最常用的一种是明考夫斯基(Minkowsky)距离：

(2)

式中：(ui,vi,wi)和(uj,vj,wj)表示任意两个体元在3个轴向上的序号；当q=2时，d2(i,j)表示的就是欧氏距离；当q=1时，d1(i,j)表示的是绝对值距离；当q→∞时，d∞(i,j)表示的是切比雪夫距离。

在实际应用中，为了精确表达地质体及地质现象、满足大比例尺定量预测需求，格网的分辨率一般要非常精细，一个矿区的体元数量甚至可以达到上百万个。如果对每个体元求取其中心点到一个或多个三维表面的距离，计算量很大，因此通常采用近似的场模型的距离量算来替代。本文设计了一种“种子生长算法”，可同时实现最短距离场的生成及路径搜索，并允许在三维地质空间中存在多个“源实体”，以及体元可加载“费用”权值(默认等于1)来表达距离场的非均质性。

3.2 邻接体元的编码

三维场模型的距离是以各体元的中心点为节点、以体元的邻接关系作为连接进行计算的。三维场中对每个体元有一个3×3×3的以该体元为中心的邻域，用0--26对其邻域内的体元进行编码，该编码也用来表示从源体元指向邻接体元的方向，方向编码(Dir)为0则指向自身。每个体元最多与26个体元相邻，体元之间的邻接形式有3种：面邻接6个(编码1--6)，与源体元共用一个面，距离源体元1单元；边邻接12个(编码7--18)，与源体元共用一条边，距离源体元2(1/q)单元；点邻接8个(编码19--26)，与源体元共用一个顶点，距离源体元3(1/q)单元，如图3所示。

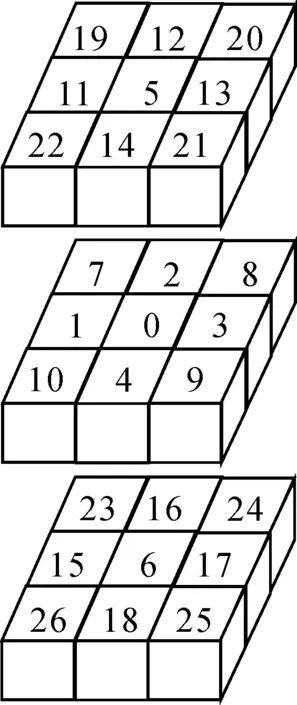
图3 26个邻接体元的编码Fig.3 Coding of 26 adjacent voxels

3.3 加权最短距离场的生成

设源体元k和邻接体元k′加载的“费用”权值分别为Ck和Ck′，则源体元k到其目标体元k′的加权距离为

(3)

应用“种子生长算法”同时生成最短距离场及最短路径搜索的具体步骤(图4)如下：

第一步，将离散的体元分成2个集合，特征体元集合S和目标体元集合S′。集合S为“源实体”占据的体元，其距离场值为0(近似值)，其向量的Dir为0；集合S′为三维场中其他体元集合，其距离场值默认为∞，其向量的Dir为无效值-1。

第二步，以集合S中的每个体元o为“种子”，向其26个相邻体元“生长”，按公式(3)计算相邻体元o′的加权距离场值：

(4)

如果FdC(o′)小于o′原距离场值，则用FdC(o′)替换原距离场值(反之，沿用原距离场值)，并将向量o′o(从体元o′中心节点指向体元o中心节点的向量)的Dir存储在体元o′中。

第三步，从集合S′中选取距离场值最小的体元k作为“种子”，向体元k的26个相邻体元“生长”，按公式(3)计算相邻体元k′的加权距离场值：

(5)

如果FdC(k′)小于k′原距离场值，则替换之(反之，沿用原距离场值)，并将向量k′k的Dir存储在体元k′中，然后将体元k从集合S′移动到集合S中。

第四步，循环执行第三步，直至集合S′为空时停止，成功生成最短距离场。

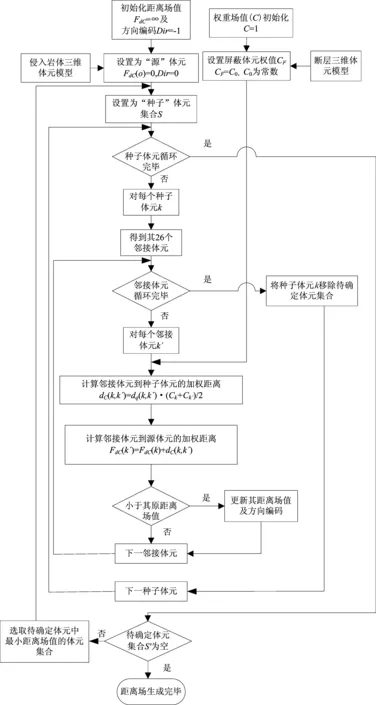
图4 “种子生长法”加权最短距离场生成算法流程图Fig. 4 Flowchart of ‘seed-growing’ weighted shortest distance field generation

第五步，对任意体元t′执行路径搜索时，只需读取其向量方向编码，获取指向的体元t；再读取体元t的向量方向编码，获取其指向的体元。循环调用该过程，直至最终体元的Dir为0(源实体所占据的体元)，就得到了体元t′到达“源实体”的一条最短路径。

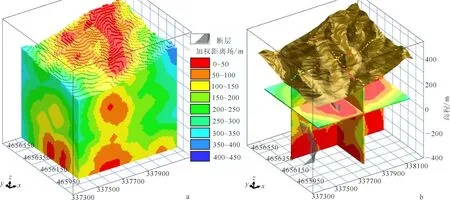
a.全局图；b.栅状图。图5 某铜矿区侵入岩体的最短距离场Fig.5 Intrusive rocks’ shortest distance field of a copper deposit area

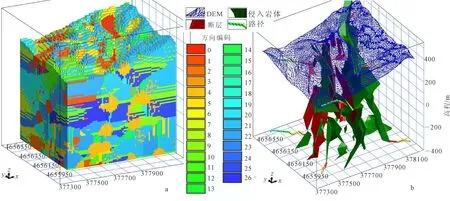
a.方向编码；b.路径回溯。图6 根据方向编码进行路径回溯Fig.6 Tracing back a path according to direction code

4 计算结果

为了分析研究区内与成矿作用有关的侵入岩体的热力场分布和围岩蚀变情况，采用文中的“种子生长算法”对三维地质模型中的侵入岩体计算了最短距离场，将定性数据转变为定量数据，实现对空间数据的深加工，见附录A2和附录A3。最短距离场可克服三维GIS缓冲区分析只能识别出距离侵入岩体某一范围内的邻域(且该邻域是均质的)、且无法反映出侵入岩体热力场依距离渐变性的缺陷(图5a)；设置断层对应体元的“费用”权值为10(其他体元费用权值默认为1)，使断层所在单元在距离场计算中起到了屏蔽作用，以模拟断层对热力场的空间分划作用(图5b)。

每个体元除存储其到最近的源体元的距离值外，还存储有用于追踪距离变换的上一级体元的方向向量编码，如图6a所示；通过逐级追踪直至源为止，可以得到一条体元到源体元的最短路径(见附录A4)，如图6b所示。

5 结论

本文提出对与成矿作用有关的侵入岩体计算最短距离场，能够表达断层对地质空间分划作用的非均质性；在生成距离场的同时通过记录上级体元方向编码，使每个单元均可回溯出一条到最近源体元的最短路径。进一步研究将包括提取地质空间场内岩体封闭边界通过的体元，从而支持同时计算岩体内部和外部的距离场值(内部场值设置为负值，外部场值设置为正值，边界处场值为零值)，为更精细地分析侵入岩体的热力场分布提供支撑。利用场分析技术对三维地质实体模型进行深层次和组合信息挖掘，既能借助三维可视化仿真环境，将地、物、化、遥等多源地学空间数据集成在统一的三维空间数据场构架下，又为成矿定量预测模型中三维地质变量的构造和选择提供了支持。

红透山矿业有限公司石长岩副总经理、辽宁有色地质局101队地勘院杨铁军副院长在资料收集、坑道调查工作中给予了细致周密的安排和热情协助，国家地理信息系统工程技术研究中心与中南大学共建“MAPGIS实验室”为本研究工作提供了MAPGIS软件，在此一并表示感谢！

附录：Microsoft SQL Server 2012源代码

A1 建立初始三维空间数据场

--建立地质空间数据场表格HTS101010F

CREATE TABLE HTS101010F(

ID INT NOT NULL UNIQUE,--唯一的ID

IX INT NOT NULL,--X方向序号

IY INT NOT NULL,--Y方向序号

IZ INT NOT NULL,--Z方向序号

X INT NOT NULL,--X坐标，m

Y INT NOT NULL,--Y坐标，m

Z INT NOT NULL,--Z坐标，m

TO_SOURCE CHAR(1),--是否是源体元，1-源体元/0-其他体元

WEIGHTNESS SMALLINT,--权重值，默认值为1，断层体元为10

PATH_TO SMALLINT,--到上一级体元的方向编码

DISTANCE DECIMAL(9,3),--最短距离场值，m

CUR_STATE CHAR(1)--是否计算距离场，1-已计算/0-未计算

);

--对唯一的ID建立索引

CREATE UNIQUE INDEX HTS101010FID ON HTS101010F(ID);

--对Z方向序号建立索引

CREATE INDEX HTS10101FIZ ON HTS101010F(IZ);

--对Y方向序号建立索引

CREATE INDEX HTS10101FIY ON HTS101010F(IY);

--对X方向序号建立索引

CREATE INDEX HTS10101FIX ON HTS101010F(IX);

--向地质空间数据场表格中插入记录的存储过程

CREATE PROCEDURE [dbo].[InsertAllReords]

@minx int, --X坐标最小值

@miny int, --Y坐标最小值

@minz int, --Z坐标最小值

@maxx int, --X坐标最大值

@maxy int, --Y坐标最大值

@maxz int, --Z坐标最大值

@minix int,--X方向序号最小值

@miniy int,--Y方向序号最小值

@miniz int,--Z方向序号最小值

@maxix int,--X方向序号最大值

@maxiy int,--Y方向序号最大值

@maxiz int,--Z方向序号最大值

@nx int,--X方向单元数

@ny int,--Y方向单元数

@step int--单元尺寸，步长

BEGIN

Declare @ix int = @minix, @iy int = @miniy, @iz int = @miniz

Declare @id int, @x int, @y int, @z int

Declare @dem float

-- 删除三维地质空间数据场表格中的记录

DELETE FROM HTS101010F

set @iy = @miniy

While (@iy <= @maxiy)

Begin --开始Y方向循环

set @y = @miny + (@iy-@miniy)*@step

set @ix = @minix

While (@ix <= @maxix)

Begin --开始X方向循环

set @x = @minx + (@ix-@minix)*@step

--根据X、Y坐标从DEM数据表DZT5KL01E中获取地表高程值

select @dem = (Select dem from DZT5KL01E WHERE X=@x and Y=@y)

set @iz= @miniz

While (@iz <= @maxiz)

Begin --开始Z方向循环

set @id = (@iz-1)*@nx*@ny + (@iy-1)*@nx + @ix

set @z = @minz + (@iz-@miniz)*@step

if(@z > @dem) break --如果高于地表高程，不插入表记录

--向三维地质空间数据场表格HTS101010F中插入记录

Insert into HTS101010F

values(@id, @ix, @iy, @iz, @x, @y, @z, 0,1,null,null,0)

set @iz = @iz+1

END --结束Z方向循环

set @ix = @ix+1

END --结束X方向循环

set @iy = @iy+1

END --结束Y方向循环

END

A2 设置源体元和距离场权值

-- 将侵入岩体通过的体元设置为源体元

update HTS101010f

set to_source = '1', PATH_TO = 0, Distance = 0, CUR_STATE = 0

where hts101010f.id in

(select hts101010.id from HTS101010 where HTS101010.xp > 0);

-- 设置其他体元的的距离场值为初始值99999

update HTS101010f

set DISTANCE = 99999

where DISTANCE IS NULL

-- 将断层通过的体元的权值设置为10

update HTS101010f

set weightness = 10

where hts101010f.id in

(select hts101010.id from HTS101010 where HTS101010.f > 0);

A3 建立非均质的最短距离场

-- 生成最短距离场的存储过程

CREATE PROCEDURE[dbo].[DistanceFields]

BEGIN

DECLARE @MINDIST REAL = 0

WHILE @MINDIST!=-999 --返回距离值无效时结束循环

BEGIN

SET @MINDIST = -999

--对当前最小距离的体元运行生长算法

EXEC MinDistanceGrowth @MINDIST OUTPUT --返回当前最小距离

END

-- 当前最小距离值体元生长的存储过程

CREATE PROCEDURE [dbo].[MinDistanceGrowth]

@mindist real = -9999 out --返回当前最小距离

BEGIN

-- 获取距离场计算状态未知的最小距离值的体元

set @mindist = (select min(distance) from HTS101010F where distance is not null and CUR_STATE=0) --获得当前的最小距离值

-- 更新当前最小距离值的体元的距离场计算状态为完成

UPDATE HTS101010F SET CUR_STATE =1 WHERE DISTANCE = @mindist

-- 定义光标获取当前最小距离值的所有体元的ID和权值

DECLARE pIDs CURSOR FOR select ID,WEIGHTNESS from HTS101010F where distance= @mindist order by ID

OPEN pIDs --打开光标

DECLARE @ID INT= 0, @WEIGHT SMALLINT = 0

fetch next from pIDs into @ID, @WEIGHT--读取第一个体元的ID和权值

while @@fetch_status = 0 --如果当前光标无效，结束循环

BEGIN

-- 更新该体元邻近26个体元的距离场值

EXEC UpdateNeighborDistance @ID,@mindist,@WEIGHT

fetch next from pIDs into @ID, @WEIGHT --读取下一个体元的ID和权值

END

CLOSE pIDs --关闭光标

Deallocate pIDs --销毁光标

END

-- 根据当前体元距离值更新邻近体元的值

CREATE PROCEDURE [dbo].[UpdateNeighborDistance]

@ID INT = 0,--当前体元ID

@DIST real = -999,--当前体元距离场值

@WEIGHT SMALLINT = -1--当前体元费用权值

BEGIN

DECLARE @IX INT=0, @IY INT=0, @IZ INT=0

-- 根据ID获取X、Y、Z方向上的序号

EXEC GetXYZfromID @ID,@IX OUTPUT,@IY OUTPUT,@IZ OUTPUT

-- 定义光标选取当前体元邻近的26个体元

DECLARE pNeighbors CURSOR FOR SELECT

ID,IX,IY,IZ,CUR_STATE,DISTANCE,WEIGHTNESS,PATH_TO

FROM HTS101010F

WHERE IX >=@IX-1 AND IX <=@IX+1

AND IY>=@IY-1 AND IY <=@IY+1

AND IZ>=@IZ-1 AND IZ <=@IZ+1

AND CUR_STATE = 0

AND DISTANCE > @Dist -- 大于当前体元距离

ORDER BY ID

OPEN pNeighbors --打开光标

DECLARE @NID INT = 0, @NIX INT=0, @NIY INT=0, @NIZ INT=0,

@NSTATE SMALLINT=0, @NDIST REAL = 0,@NWEIGHT SMALLINT =0, @NPATH SMALLINT =0

fetch next from pNeighbors into --读取第一个邻近体元

@NID,@NIX,@NIY,@NIZ,@NSTATE,@NDIST,@NWEIGHT,@NPATH

while @@fetch_status = 0 --如果当前光标无效结束循环

BEGIN

DECLARE @TEMPDIST REAL = 99999

IF @NSTATE = 0 --如果该邻近体元未完成距离场计算

BEGIN

-- 根据邻近体元的位置设置其距离场值@TEMPDIST(略)

-- 根据邻近体元的位置设置其方向编码@NPATH(略)

IF @TEMPDIST < @NDIST --小于原距离值

BEGIN

-- 更新邻近体元的距离场值和方向编码

UPDATE HTS101010F SET

PATH_TO = @NPATH,

DISTANCE = @TEMPDIST

WHERE ID = @NID

END

--读取下一个邻近体元

fetch next from pNeighbors into

@NID, @NIX,@NIY,@NIZ,@NSTATE,@NDIST,@NWEIGHT,@NPATH

END

CLOSE pNeighbors --关闭光标

Deallocate pNeighbors --销毁光标

END

A4 到源体元的最短路径回溯

-- 获得当前体元到源体元的最短路径

CREATE PROCEDURE GetPathByID

@id int

BEGIN

DECLARE @code int = 0

--获取当前体元的方向编码

SET @code = (select PATH_TO from HTS101010F where ID = @id)

--建立临时表用于存储路径所经体元的ID和方向编码

DECLARE @PathTable TABLE(ID int,SrcCode int)

--将当前体元添加到临时表

INSERT INTO @PathTable VALUES (@id,@code)

WHILE @CODE !=0 --如果当前体元是源体元，结束循环

BEGIN

declare @nid int = 0

-- 获得上一级体元的ID

exec GetNeighborByCode @id,@code,@nid output

-- 获取上一级体元的的方向代码

SET @code = (select PATH_TO from HTS101010F where ID = @nid)

-- 将上一级体元添加到临时表

INSERT INTO @PathTable VALUES (@nid,@code)

set @id = @nid -- 设置上一级体元为当前体元

END

-- 将路径经过的体元从三维数据场表格中选择出来

select * from HTS101010F where ID in ( select ID from @PathTable )

ORDER BY DISTANCE DESC

END

[1] Houlding S W. 3D Geoscience Modeling: Computer Techniques for Geological Characterization[M]. Berlin: Springer-Verlag, 1994.

[2] Mallet J L. Geomodeling[M]. New York: Oxford University Press, 2002.

[3] Wu Q, Xu H, Zou X K. An Effective Method for 3D Geological Modeling with Multi-Source Data Integration[J]. Computers and Geosciences, 2005, 31(1): 35-43.

[4] 吴立新, 车德福,郭甲腾. 面向地上下无缝集成建模的新一代三维地理信息系统[J]. 测绘工程, 2006, 15(5): 1-6. Wu Lixin, Che Defu, Guo Jiateng. The New 3DGIS for Seamless Integration of Terrain Overground and Underground Entities[J]. Engineering of Surveying and Mapping, 2006, 15(5): 1-6.

[5] 潘懋, 方裕,屈红刚. 三维地质建模若干基本问题探讨[J]. 地理与地理信息科学, 2007, 23(3): 1-5. Pan Mao, Fang Yu, Qu Honggang. Discussion on Several Foundational Issues in Three-Dimensional Geological Modeling[J]. Geography and Geo-Information Science, 2007, 23(3): 1-5.

[6] Zhang B Y, Wu X B, Wang L F, et al. The Preliminary Research of Feature-Based 3D Geological Modeling[C]//2nd Conference on Environmental Science and Information Application Technology (ESIAT’2010). Wuhan: IEEE Computer Society, 2010: 321-325.

[7] Zu X F, Hou W S, Zhang B Y, et al. Overview of Three-Dimensional Geological Modeling Technology[C]//Lee G. International Conference on Future Computer Supported Education (FCSE). Seoul: IERI Procedia, 2012: 921-927.

[8] Zu X F, Zhang B Y, Luo J, et al. 3D Modeling of Tunnel Engineering Based on Geological Body[C]//Lee G. International Conference on Future Computer Supported Education (FCSE). Seoul: IERI Procedia, 2012: 928-934.

[9] 张宝一, 尚建嘎, 吴鸿敏, 等. 三维地质建模及可视化技术在固体矿产储量估算中的应用[J]. 地质与勘探, 2007, 43(2): 76-81. Zhang Baoyi, Shang Jianga, Wu Hongmin, et al. Application of 3D Geological Modeling and Visualization in Solid Mineral Resource Estimation[J]. Geology and Prospecting, 2007, 43(2): 76-81.

[10] 张宝一, 吴湘滨, 王丽芳, 等. 红透山铜矿外围隐伏矿体三维定量预测[J]. 中国有色金属学报, 2012, 22(3): 863-871. Zhang Baoyi, Wu Xiangbin, Wang Lifang, et al. 3D Quantitative Prediction of Concealed Ore-Body in Surrounding Areas of Hongtoushan Copper Deposit[J]. The Chinese Journal of Nonferrous Metals, 2012, 22(3): 863-871.

[11] 张宝一, 吴湘滨, 王丽芳, 等. 三维地质建模及应用实例[J]. 地质找矿论丛, 2013, 28(3): 328-336. Zhang Baoyi, Wu Xiangbin, Wang Lifang, et al. Three-Dimensional Geological Modeling and the Application Cases[J]. Contributions to Geology and Mineral Resources Research, 2013, 28(3): 328-336.

[12] 程朋根, 刘少华, 王伟, 等. 三维地质模型构建方法的研究及应用[J]. 吉林大学学报:地球科学版, 2004, 34(2): 309-313. Cheng Penggen, Liu Shaohua, Wang Wei, et al. Study and Application of a New 3D Geological Model Construction Method[J]. Journal of Jilin University: Earth Science Edition, 2004, 34(2): 309-313.

[13] 程朋根, 王承瑞, 甘卫军, 等. 基于多层DEM与QTPV的混合数据模型及其在地质建模中的应用[J]. 吉林大学学报:地球科学版, 2005, 35(6): 806-811. Cheng Penggen, Wang Chengrui, Gan Weijun, et al. A Hybrid 3D Data Model Based on Multi-DEMs and QTPVs and Its Application in Geological Modeling[J]. Journal of Jilin University:Earth Science Edition, 2005, 35(6): 806-811.

[14] Calcagno P, Chilès J P, Courrioux G, et al. Geological Modelling from Field Data and Geological Knowledge: Part I: Modelling Method Coupling 3D Potential-Field Interpolation and Geological Rules[J]. Physics of the Earth and Planetary Interiors, 2008, 171(1/2/3/4): 147-157.

[15] De Kemp E A. 3-D Visualization of Structural Field Data: Examples from the Archean Caopatina Formation, Abitibi Greenstone Belt, Quebec, Canada[J]. Computers and Geosciences, 2000, 26(5): 509-530.

[16] Jessell M. Three-Dimensional Geological Modelling of Potential-Field Data[J]. Computers and Geosciences, 2001, 27(4): 455-465.

[17] Shi W. Development of A Hybrid Model for 3D GIS[J]. Geo-Spatial Information Science, 2000, 3(2): 6-12.

[18] Payne B A,Toga A W. Distance Field Manipulation of Surface Models[J]. Computer Graphics and Applications, IEEE, 1992, 12(1): 65-71.

[19] 李芳玉. 基于三维栅格的GIS距离分析算法研究与应用[J]. 计算机工程与应用, 2008, 44(15): 246-248. Li Fangyu. Research and Application of Distance Analysis Based on 3D Raster GIS[J]. Computer Engineering and Applications, 2008, 44(15): 246-248.

[20] 李莹, 肖克炎,陈建平. 基于立方体模型的三维矿体模拟与资源评估[J]. 地质通报, 2010, 29(10): 1547-1553. Li Ying, Xiao Keyan, Chen Jianping. Ore Body Simulation and Resource Assessment Based on Three-Dimensional Cube Model[J]. Geological Bulletin of China, 2010, 29(10): 1547-1553.

[21] 陈建平, 陈勇, 朱鹏飞, 等. 数字矿床模型及其应用:以新疆阿勒泰地区可可托海3号伟晶岩脉稀有金属隐伏矿预测为例[J]. 地质通报, 2011, 30(6): 630-641. Chen Jianping, Chen Yong, Zhu Pengfei, et al. Digital Ore Deposit Model and Its Application: A Case Study of the Prognosis of the Koktokay No.3 Pegmatite Dike Concealed Rare Metal Deposit in Altay Area of Xinjiang[J]. Geological Bulletin of China, 2011, 30(6): 630-641.

[22] 安聪荣, 刘展, 黄荣刚, 等. 基于三维栅格模型的最短距离等值面提取[J]. 计算机工程, 2011, 37(8): 7-9. An Congrong, Liu Zhan, Huang Ronggang, et al. Shortest Distance Isosurface Extraction Based on Three-Dimensional Raster Model[J]. Computer Engineering, 2011, 37(8): 7-9.

[23] 毛先成, 唐艳华,邓浩. 地质体的三维形态分析方法与应用[J]. 中南大学学报:自然科学版, 2012, 43(2): 588-595. Mao Xiancheng, Tang Yanhua, Deng Hao. Three-Dimensional Morphological Analysis Method for Geologic Bodies and Its Application[J]. Journal of Central South University:Science and Technology, 2012, 43(2): 588-595.

[24] 毛先成, 戴塔根, 吴湘滨, 等. 危机矿山深边部隐伏矿体立体定量预测研究:以广西大厂锡多金属矿床为例[J]. 中国地质, 2009, 36(2): 424-435. Mao Xiancheng, Dai Tagen, Wu Xiangbin, et al. The Stereoscopic Quantitative Prediction of Concealed Ore Bodies in the Deep and Marginal Parts of Crisis Mines: A Case Study of the Dachang Tin Polymetallic Ore Deposit in Guangxi[J]. Geology in China, 2009, 36(2): 424-435.

[25] 毛先成, 邹艳红, 陈进, 等. 危机矿山深部、边部隐伏矿体的三维可视化预测:以安徽铜陵凤凰山矿田为例[J]. 地质通报, 2010, 29(2/3): 401-413. Mao Xiancheng, Zou Yanhong, Chen Jin, et al. Three-Dimensional Visual Prediction of Concealed Ore Bodies in the Deep and Marginal Parts of Crisis Mines: A Case Study of the Fenghuangshan Ore Field in Tongling, Anhui, China[J]. Geological Bulletin of China, 2010, 29(2/3): 401-413.

A Path-Savable Shortest-Distance Field Generating Algorithm in Three-Dimensional Heterogenetic Space

Wang Lifang1, Wu Xiangbin1, Zhang Baoyi1,2, Li Xiaoli1, Yang Li1

1.MOEKeyLaboratoryofMetallogenicPredictionofNonferrousMetalsandGeologicalEnvironmentMonitoring/SchoolofGeosciencesandInfo-Physics,CentralSouthUniversity,Changsha410083,China2.StateKeyLaboratoryofGeologicalProcessesandMineralResources,ChinaUniversityofGeosciences,Wuhan430074,China

A comprehensive study on three-dimensional (3D) spatial information is highly demanded for a quantitive prediction of mineralization. The difficulties are often confronted in geological feature quantitive expression and deep-seated information extraction. A shortest-distance field generating algorithm in 3D heterogenetic space is developed, which can track back to the shortest path from an object voxel to the source voxel. The algorithm has been used to a copper mine district for its deeper and comprehensive information based on the 3D geological entity model. A shortest-distance field to the intrusive rocks is calculated to analyze the geological problems, such as thermodynamic field and the alteration of surrounding rock in consideration of the roles played by the faults in dividing 3D geological space.

distance field; three-dimensional; heterogenetic; path；metallogenic prediction

10.13278/j.cnki.jjuese.201504305.

2014-10-29

国家自然科学基金项目(41302259)；“十一五”国家科技支撑计划项目(2008BAB34B02)

王丽芳(1979--)，女，博士研究生，工程师，主要从事三维地质建模研究，E-mail:csuwlf@139.com

张宝一(1979--)，男，在站博士后，副教授，主要从事地理信息科学研究，E-mail:zhangbaoyi@csu.edu.cn。

10.13278/j.cnki.jjuese.201504305

P628.3

王丽芳，吴湘滨，张宝一，等. 一种可存储路径的三维非均质空间最短距离场生成算法.吉林大学学报:地球科学版,2015,45(4):1257-1268.

Wang Lifang, Wu Xiangbin, Zhang Baoyi, et al. A Path-Savable Shortest-Distance Field Generating Algorithm in Three-Dimensional Heterogenetic Space.Journal of Jilin University:Earth Science Edition,2015,45(4):1257-1268.doi:10.13278/j.cnki.jjuese.201504305.