基于节点密度的改进型DV－Hop 算法

黄俊杰，刘士兴，干小宇，尹 坤

(合肥工业大学 电子科学与应用物理学院，安徽 合肥 230009)

无线传感器网络是由部署在一定区域内的许多具有采集数据、处理数据和传输数据功能的传感器节点组成，节点之间通过无线通信的方式构成一个多跳的自组织网络。无线传感器网络中有很多特定的应用需要获取节点的地理位置信息，且较多网络的运行与管理需节点位置信息的辅助。因此，对无线传感器网络中节点定位机制以及定位算法的研究有着重要意义［1］。

根据定位机制，将现有的定位算法分为两种，即基于测距的定位算法(Range－based)和与距离无关(Range－free)的定位算法［2］。前者需额外增加硬件来测量相邻节点间的绝对距离或者方位，并利用节点间的实际距离来计算未知节点的位置;后者无需额外硬件测量节点间的绝对距离或方位，而是利用节点间的估计距离计算未知节点的位置。常用的与距离相关的定位技术有RSSI、TOA、TDOA 和AOA。这类算法定位精度相对较高，但是成本与能耗开销也较大。与距离无关的定位算法利用网络的连通性进行定位，常用的有质心算法、DV－Hop［3］、Amorphous［4］、APIT［5］等，这类算法成本和功耗较低，应用更加广泛。

DV－Hop 算法是目前应用最为广泛的定位算法之一，针对DV－Hop 算法改进研究，本文提出了提高节点定位精度的加权DV－Hop 算法和降低功耗的基于节点密度的定位算法。

1 DV－HOP 算法

DV－Hop 定位算法是由Niculescud 等人提出的一种基于距离矢量计算跳数的算法。其基本思想是将未知节点到信标节点之间的距离用平均跳距和两者之间跳数的乘积表示，具体步骤如下［6］:

(1)信标节点信息泛洪广播和所有节点获取距离信标节点的最小跳数。信标节点采用泛洪广播方式将其位置信息采用分组形式传递给其邻居节点，广播的信息包格式为:{Idi，xi，yi，Hopsi}，其中包含了该节点的标识Idi、位置坐标(xi，yi)以及跳数信息Hopsi，初始Hopsi的值为0。接收到此数据的每个节点将此信息记录下来，然后继续向其邻居节点广播，每广播一次就将Hopsi加1，并将分组信息以{Idi，xi，yi，Hopsi}的格式存储到自身的数据表中。当节点接收到有相同Id的数据包时，对两个数据包中的Hopsi进行比较，如果新的跳数小于原表中保存的跳数，则用新跳数替换节点中的信息，这就意味着找到了一条更短的到达该信标节点的路径。如果新的跳数大于节点中的跳数，则丢弃该数据包，也不再进行转发。

(2)计算未知节点与信标节点的估计距离。经第一步后，每个信标节点获得了其他信标节点的位置和最小跳数。此时通过式(1)计算网络中平均每跳的距离

式(1)中，(xi，yi)，(xj，yj)为信标节点i，j 的坐标;hi为信标节点i 与j(i ≠j)之间的跳段数;HopSize 为求出的平均跳距。

(3)信标节点将平均跳距广播到网络，通过式(2)计算未知节点到信标节点的估计距离du，i

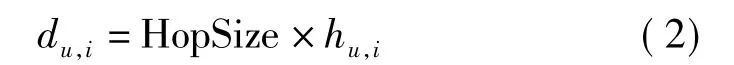
当未知节点得到3 个或更多节点之间的距离后，再通过3 边测量法［7］或极大似然估计等数学方法计算未知节点的坐标。

2 加权DV－Hop 算法

在实际使用中，DV－Hop 算法的定位精度受到节点密度及其分布情况影响。网络中信标节点的密度越大，分布越合理，则定位精度越高，反之则定位误差大。

2.1 DV－Hop 算法误差分析

在实际使用中，部署信标节点的成本较高，因而信号节点的总数不会很多。另外，节点通常是随机放置在探测环境中，难以保证信标节点分布的合理性［8－9］。综上，实际使用中，DV－Hop 定位算法会有较大的定位误差。

DV－Hop 定位算法使用跳段数与平均每跳距离的乘积来得到未知节点与信标节点的估计距离。该种估算方法时会有较大误差，如图1 所示对应的网络拓扑结构。

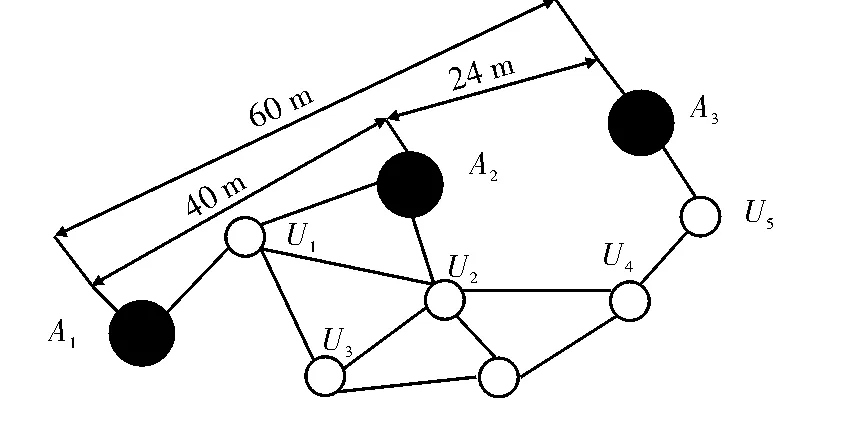
图1 DV－Hop 误差分析

其中A1，A2和A3为信标节点，U1，U2，U3，U4，U5和A为未知节点。对于未知节点A，由于A2离其最近，所以A 应从A2获取HopSize 值。由式(1)得HopSize=(40+25)/(2+5) =10.7，那么3 个信标节点与A 之间的距离分别为A1:10.7×3，A2:10.7×2，A3:10.7×3。但A 与3 个信标节点的真实距离分别为:50 m，40 m，50 m，这使得定位误差较大。在该网络中，A2与A3真实距离很小，仅略大于通信半径，用A2与A3来估算每跳距离，所得的误差就较大。

2.2 加权DV－Hop 算法

针对上文所提关于DV－Hop 定位算法中使用相同的平均跳距来计算未知节点到信标节点间距离的定位误差问题，有学者提出了加权DV－Hop 定位算法［10－11］。该算法的基本思想是在DV－Hop 定位算法中，通过加权系数的大小体现不同信标节点对未知节点位置坐标运算中的影响力大小，然后通过加权平均跳距估算未知节点的位置。实际使用中，不同信标节点的加权系数Wi通过式(3)确定

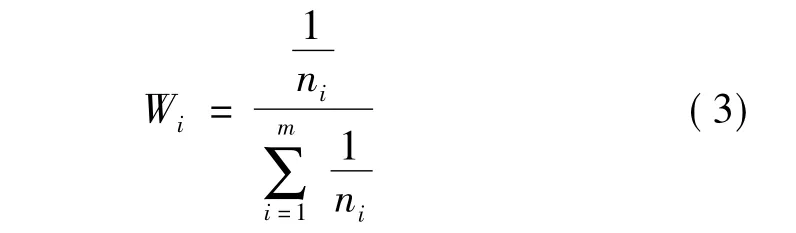
其中，ni表示信标节点i 与未知节点之间的跳数。

根据式(4)，得未知节点的加权平均跳距为

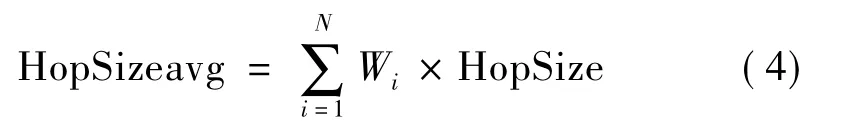
使用加权后的平均跳距，代入DV－Hop 定位算法的第三步，计算出未知节点到信标节点之间的距离，再通过3 边测量法或者极大似然估计等数学方法计算出未知节点的坐标。

3 基于节点密度的定位算法

加权DV－Hop 定位算法改进了DV－Hop 定位算法中对平均跳距的计算，但在该算法的执行过程中仍然需进行两次泛洪广播，需要较大的通信开销，也增加了节点的能耗。Amorphous 定位算法使用节点通信半径代替DV－Hop 定位算法中的平均跳距，该方法只需一次泛洪广播，但定位误差较大。为此，本文提出了基于节点密度的定位算法。

假设二维平面中节点信息的传播是以节点为中心，节点通信半径为半径的圆形区域，且节点之间的信息传播是相互的。若一个面积为S 的仿真区域中有n个节点，则此仿真区域的节点密度为

仿真区域内某一个节点的邻居节点数为N，计算方法如下

由Kleinrock－Silvester 式［12－13］可知节点的每跳距离与节点的通信半径和节点的邻居节点数存在一定的关系

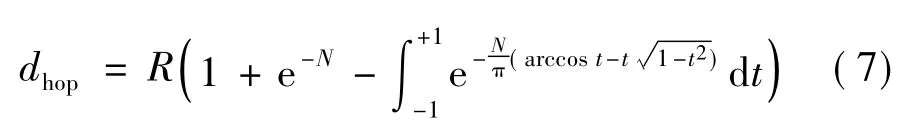
式中，dhop为计算出的跳距;R 为节点通信半径;N 为邻居节点数目。当N 已知时，dhop便可用R 表示，如图2所示。

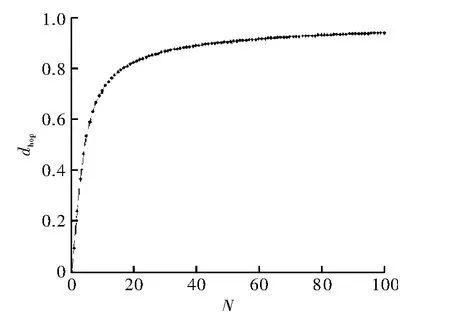
图2 邻居节点数与每跳平均距离关系

若直接使用该跳距乘以最小跳距计算未知节点到信标节点之间的距离，将会出现较大误差，因而参考加权DV－Hop 定位算法的思想，在信标节点和未知节点之间的计算进行加权处理，得出加权跳距

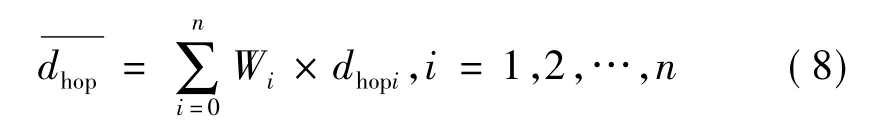
通过式(8)，计算出的加权平均跳距乘以跳数，就可得到未知节点到信标节点i 的距离。当获得3 个或以上距离信标节点的距离后，就可用3 边测量法或者极大似然估计等数学方法计算出未知节点的坐标。

4 算法仿真验证

采用Matlab 对上述算法进行仿真，并对仿真数据进行分析。仿真环境为100 m×100 m 的正方形区域，未知节点和锚节点随机分布。下面对DV－Hop算法和改进算法的定位误差和通信开销在不同锚节点数目下进行评估。针对固定的锚节点数目，重复做50 次仿真，取平均值。假设未知节点的估算位置为(xc，yc)，节点的实际位置为(xi，yi)，则未知节点的定位误差为

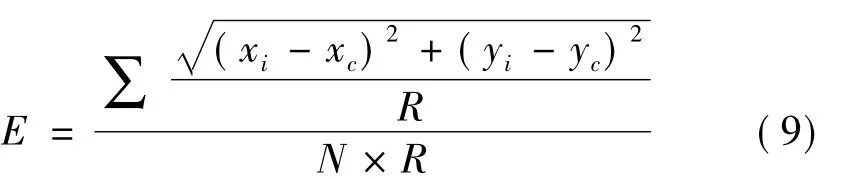
式中，R 为节点的通信半径;N 为未知节点的个数。

仿真得到的定位误差如图3 和图4 所示，采用加权DV－Hop 定位算法得到的定位误差最小，基于节点密度的定位算法次之，两种改进型算法的定位精度都优于DV－Hop 定位算法。以图3 为例，在通信半径为20 m，信标节点个数为12 的条件下，DV－Hop 定位算法的误差为45.47%，基于节点密度定位算法的误差为43.09%，而加权DV－Hop 算法的定位误差为42.16%。

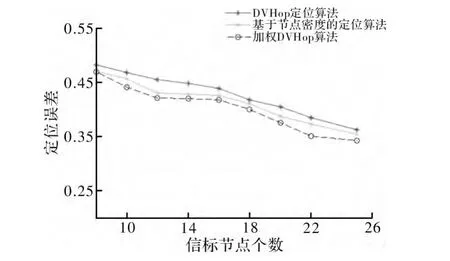
图3 节点个数与定位误差的关系(R=20 m)

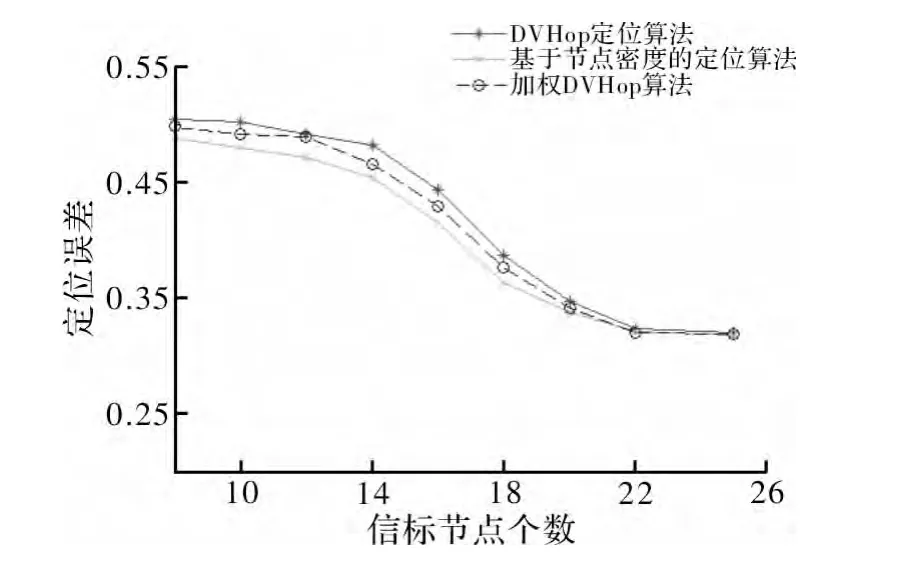
图4 节点个数与定位误差的关系(R=25 m)

通信开销是节点在定位过程中主要的能耗，为评估不同算法的通信开销，假设节点的通信半径为20 m，分别对包含不同节点数目的区域进行算法仿真，最后收集定位过程中的数据包数来体现节点的能耗，仿真过程中不考虑信息包之间的冲突与丢失。仿真结果如图5 所示，基于节点密度的定位算法比DV－Hop 定位算法和加权DV－Hop 算法功耗低。

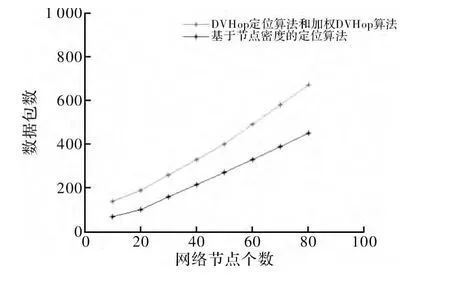
图5 算法通信开销

5 结束语

介绍了现有DV－Hop 定位算法，分析了该算法存在定位精度低和通信开销大的缺陷。加权DV－Hop定位算法有效提高了定位精度，但不能降低通信开销。通过Matlab 仿真结果表明，基于节点密度的改进型定位算法，在节点定位误差与节点的通信开销上均有明显的改善，适合于对节点能耗要求严格的场合。

本文讨论的算法均是在理想状态下进行的仿真，但现实环境中通常会因温度、湿度以及大气压强等因素对节点定位造成影响。如何在考虑这些影响因素的前提下来提高节点的定位精度还有待进一步研究。

［1］ Bulusu N，Heidemann J，Estrin D.GPS－less low cost outdoor localization for very small devices［J］.IEEE Personal Communication，2000，7(5):28－34.

［2］ 孙利民，李建中，陈渝.无线传感器网络［M］.北京:清华大学出版社，2005.

［3］ Lin Jinchao，Chen Xiaobing，Liu Haibo.Iterative algorithm for locating nodes in WSN based on modifying average hopping distances［J］.Journal on Communications，2009，30(10):107－113.

［4］ Nagpal R.Organizing a global coordinate system from local information on an amorphous computer［D］.MA USA:MIT AI Laboratory，1999.

［5］ He Tian，Huang Chengdu，Blum B M，et al.Range－free localization schemes in large scale sensor networks［C］.San Diego，USA:Proceedings of the 9th Annual International Conference on Mobile Computing and Networking，MOBICOM'2003，2003:81－95.

［6］ 李晓维，徐勇军，任丰原.无线传感器网络技术［M］.北京:北京理工大学出版社，2007.

［7］ Cao Yu，Chen Xiupeng，Yu Yang，et al.Range－free distance estimate methods using neighbor information in wireless sensor networks［C］.Proc IEEE 70th Vehicular Technology conference Fall，2009:1－5.

［8］ Tian Shuang，Zhang Xinming，Wang Xinguo，et al.A selective anchor node localization algorithm for wireless sensor networks［C］.International Conference on Convergence Information Technology(ICCIT)，2007:358－362.

［9］ Liu Shaoqiang，Pang Xinmiao，Fan Xiaoping.Improved DVHop algorithm for higher positioning accuracy［J］.Chinese Journal of Sensors and Actuators，2010，23:1179－1183.

［10］冯江，朱强，吴春春.改进的DV－Hop 定位算法研究［J］.计算机工程，2012，38(19):74－77.

［11］Chen Hongyang，Sezaki K，Deng Ping，et al.An improved DV－HOP localization algorithm for wireless sensor networks［C］.Industrial Electronics and Applications，ICIEA 3rd IEEE Conference，2008:1557－1561.

［12］Nagpal R，Shrobe H，Bachrach J.Organizing a global coordinate system from local information on an Ad Hoc sensor network［C］.Palo Alto，CA，USA:Second International Workshop，IPSN 2003，2003.

［13］Erchin Serpe Din，Qasim M Chaudhari.Synchronization in wireless sensor networks ［M］.CA USA: Science Press，2011.