基于输出反馈的建筑结构闭开环次优控制①

宋　刚， 谭　川， 陈　果

(招商局重庆交通科研设计院有限公司桥梁工程结构动力学国家重点实验室，重庆 400067)



基于输出反馈的建筑结构闭开环次优控制①

宋刚， 谭川， 陈果

(招商局重庆交通科研设计院有限公司桥梁工程结构动力学国家重点实验室，重庆 400067)

摘要：对传统的结构抗震闭开环控制算法进行改进。基于地面运动自回归模型，采用Kalman滤波利用可以量测到的地面加速度激励对未来时段即将发生的地面加速度激励进行预估，并在微分方程的求解中引入精确高效的精细积分算法。考虑到实际控制中量测全部状态变量的困难，改进算法仅需量测部分状态变量。数值仿真表明，基于输出反馈的闭开环次优控制策略能大大降低结构的地震响应。

关键词：地震激励； 输出反馈； 闭开环控制； Kalman滤波； 精细积分

0引言

近几十年来控制在理论和实际工程中都获得了很大进展[1-3]，其中线性二次型调节器(LQR)在很多工程中得到了应用[4-5]。在传统的二次型调节器问题中，目标函数定义为由结构状态和控制力向量组成的二次表达式在一定时间区段上的积分，通过庞德里亚金极大值原理或贝尔曼动态规划等方法可推导出相应的最优控制器。然而，在公式推导过程中Riccati方程是通过忽略外激励项而得出的。因此从这种意义上说，传统的二次型闭环最优控制只是一种近似的最优控制，在公式推导过程中保留外激励项的闭开环控制比闭环控制有一定的优越性。但是传统的闭开环控制需要预先知道整个控制时间区段上的外激励，这对结构抗震等工程问题来说是无法实现的。地震激励是随机的，人们无法事先知道作用在结构上的确切地震激励。相应地不需要事先知道作用在结构上的确切外激励的闭开环次优控制方法应运而生。文献[6]基于地震自回归模型，通过Kalman滤波预测一步或多步的地震动输入，采用Taylor级数进行数值积分，提出一种次优的结构抗震闭开环控制策略，并通过数值算例验证了该闭开环次优控制方法相对于其他控制方法的优点。文献[7]进一步提出具有指定稳定度的结构闭开环次优控制算法。除此之外，为了避免Riccati方程的求解和确定未来时段的地震激励，文献[8]提出一种基于多点瞬态激励的闭环控制。为了提高控制精度，文献[9]在结构瞬态闭环及瞬态闭开环控制中采用了精细积分算法。

然而，以上文献[6-9]都假定结构的全部状态可以量测，这在实际控制中往往是难以做到的。钟万勰近年来提出的精细积分法求解常微分方程精度之高[10-12]，是其他时域积分法无法比拟的。本文在文献[6-9]的基础上，提出基于输出反馈的结构抗震闭开环次优控制策略，对微分方程的求解采用精细积分法来代替文献[6]和[7]中所采用的Taylor级数展开法。

1问题描述

以单维地震动输入下的n自由度线性结构为例。假定地面均匀一致运动，结构的运动方程可写为：

(1)

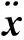
(2)

其中:

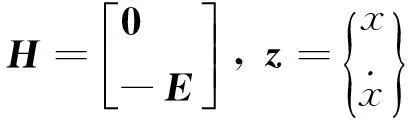
1.1基于状态反馈的闭环控制

采用性能指标

(3)

其中:tf表示地震激励持续时间。引入哈密顿函数

(4)

由方程

(5)

(6)

(7)

(8)

假定

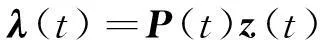
(9)

联立式(5)～式(9)，可得

(10)

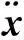
(11)

联立式(7)和(9)，可得

(12)

由式(11)解得P(t)，代入式(12)，便得到t时刻作用器应输出的控制力。

1.2基于状态反馈的闭开环控制

(13)

联立式(5)、(6)、(7)和(13)，可得

(14)

式(14)在任何时刻均成立。联立式(8)和式(14)，可得

(15)

(16)

联立式(7)和(13)，可得

(17)

2基于输出反馈的闭开环次优控制

式(15)为微分Riccati方程，借助于钟万勰近年来提出的精细算法[10-12]，微分Riccati方程可以得到简便地解决。然而在除临近tf的时间段外，P(t)在大部分时间段都近似保持为常数矩阵，把式(15)简化为代数Riccati方程来处理，见下式：

(18)

式(16)的求解需要从终端时刻进行后向积分，这需要事先知道整个控制时间区段作用在结构上的地面加速度激励。虽然地面加速度激励可以在线量测，但却无法事先知道。采用地面运动自回归模型利用Kalman滤波技术对未来时段即将发生的地面加速度激励进行预估[6]。

对于每一时间步[tk-1,tk]，式(16)的解可表示为

(19)

其中:

(20)

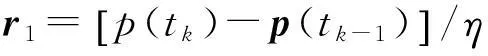
(21)

记从初始时刻到终端时刻tf的积分步数为m，由q(tf)=0，可得

(22)

(23)

利用地面运动自回归模型和Kalman滤波技术进行地面加速度激励l步预估，即在tk时刻利用过去时段(包括现在时刻)量测到的地面加速度激励估计未来时段tk+1,tk+2,…,tk+l(1≤l≤m-k)时刻的地面加速度激励。将式(23)截取前l项，可得

(24)

关于截断所带来的误差的讨论，可见文献[6-7]。式(17)需要量测结构全部状态变量，对于高阶系统，这在很多情况下是不可实现的。这里假定只有部分状态变量可测，记为y(t)：

(25)

假定

(26)

定义目标函数

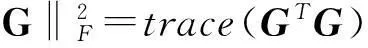
(27)

(28)

将式(24)和(28)代入式(26)中，就可得到基于输出反馈的结构闭开环次优控制。相应地忽略式(26)中的R-1BTq(t)，将式(28)代入式(26)，即得到基于输出反馈的结构闭环次优控制。

3算例

一个三层无阻尼结构受水平方向地面加速度激励，相邻层间安装主动作用器，如图1所示[6]。各层质量均为48×103kg，层间刚度分别为k1=46 420 kN/m,k2=41 780 kN/m,k3=23 210 kN/m。地面加速度激励采用El Centro地震波南北分量，地震加速度峰值为3.417 m/s2，时程记录间距为0.02 s。假定结构速度可测，即Cy=[0I] 。对未来时段地面加速度激励进行3步预估，采用基于输出反馈的闭开环控制策略对结构进行控制。取加权矩阵为

(29)

其中:μ为可调参数。不同的μ值对应不同的控制力和控制效果，经试算，取μ=1.0×108。

图1　结构模型Fig.1　Structural model

这里仅给出闭开环控制和无控时结构峰值响应对比，见表1。关于闭开环控制和闭环控制控制效果的详细比较，可见文献[6-7]。从表1可以看出，施加控制力后，结构顶层的位移、速度、加速度峰值响应和2～3层层间相对位移峰值响应都大大降低。无控时，结构顶层位移峰值为12.7 cm，施加控制力后结构顶层位移峰值降为1.1 cm。

表 1　控制前后结构响应对比

4结论

针对实际控制中量测全部状态的困难，提出一种基于输出反馈的结构闭开环次优控制算法，并对一个地震激励下的三层无阻尼结构进行数值仿真。结果表明，输出反馈闭开环次优控制可以很好地实现控制效果。

参考文献(References)

[1]Housner G W,Bergman L A,Caughey T K,et al.Structural Control:Past,Present and Future[J].Journal of Engineering Mechanics (ASCE),1997,123(9):897-958.

[2]李慧,王亚楠,杜永峰.近场脉冲型地震动作用下TMD-基础隔震混合控制结构的减震效果分析[J].地震工程学报,2013,35(2):208-212.

LI Hui,WANG Ya-nan,Du Yongfeng.An Effectiveness Analysis on Hybrid Control System of Tuned Mass Damper-base Isolation under Near-fault Pulse-like Ground Motion[J].China Earthquake Engineering Journal,2013,35(2):208-212.(in Chinese)

[3]贾斌,罗晓群,张其林,等.粘滞阻尼器对空间结构的振动控制效应[J].地震工程学报,2014,36(1):39-46.

JIA Bin,LUO Xiao-qun,ZHANG Qi-lin,et al.Vibration Control Effect of Viscous Damper on Space Structure[J].China Earthquake Engineering Journal,2014,36(1):39-46.(in Chinese)

[4]Chandak A S,Patil A J.Robust LQR Control Design of Gyroscope[J].International Journal of Advanced Computer Research,2013,3(9):7-12.

[5]Kim Y M,You K P,You J Y.Active Control of Along-wind Response of a Tall Building with AMD Using LQR Controller[J].Applied Mechanics and Materials,2014,491: 1063-1067.

[6]Bakioglu M,Aldemir U.A new Numerical Algorithm for Sub-optimal Control of Earthquake Excited Linear Structures[J].International Journal for Numerical Methods in Engineering,2001,50(12):2601-2616.

[7]Aldemir U,Bakioglu M.Active Structural Control Based on the Prediction and Degree of Stability[J].Journal of Sound and Vibration,2001,247(4):561-576.

[8]Akhiev S S,Aldemir U,Bakioglu M.Multipoint Instantaneous Optimal Control of Structures[J].Computers and Structures,2002,80(11):909-917.

[9]李金桥,于建华.基于精细积分的结构主动最优控制算法[J].西南交通大学学报, 2004,39(1):77-81.

LI Jin-qiao,YU Jian-hua.Algorithm of Optimal Active Structural Control Based on Precise Integration[J].Journal of Southwest Jiao Tong University,2004,39(1):77-81.(in Chinese)

[10]钟万勰.线性二次最优控制的精细积分法[J].自动化学报,2001,27(2):166-173.

ZHONG Wan-xie.The Precision Integration of LQ Control Problems[J].Acta Automatica Sinica,2001,27(2):166-173.(in Chinese)

[11]钟万勰.卡尔曼-布西滤波的精细积分[J].大连理工大学学报,1999,39(2):504-513.

ZHONG Wan-xie.Precise Integration of Kalman-Bucy Filtering Problems[J].Journal of Dalian University of Technology,1999,39(2):504-513.(in Chinese)

[12]ZHONG Wan-xie.On Precise Integration Method[J].Journal of Computational and Applied Mathematics,2004,163(1):59-78.

Closed/Open-loop Sub-optimal Control of Structures Based

on Output Feedbacks

SONG Gang, TAN Chuan, CHEN Guo

(StateKeyLaboratoryofBridgeEngineeringStructuralDynamics,ChinaMerchantsChongqingCommunications

Research&DesignInstituteCo.Ltd.,Chongqing400067,China)

Abstract：Most recent studies have been based on the application of linear quadratic regulator control to earthquake-excited structures. In linear quadratic regulator control problems, the objective function is defined as the integral of a quadratic expression in the control interval with respect to structural states and control vectors, and the optimal regulator can be derived using Pontryagin’s maximum principle or Bellman’s method of dynamic programming. In traditional linear quadratic regulator control problems, the Riccati equation is obtained without considering the earthquake excitation term. To optimize control and satisfy the optimality condition, in this study, we propose a new closed/open-loop control strategy for structures under earthquake excitation. We derive an analytical solution to a linear regulator problem for structural control without neglecting unknown disturbances. The optimal regulator depends on both the state and disturbances. The solution for this closed/open-loop control requires the knowledge of the earthquake in the control interval, which is approximated based on the real-time prediction of near-future earthquake excitation using the Kalman filtering technique. Earthquake excitation is modeled as an autoregressive process. The prediction algorithm can predict seismic excitation in the near future with high accuracy, although it lacks prediction accuracy for more distant future events. Considering the measurement difficulty of all state variables, especially for some high-order systems, the proposed control strategy only requires the measurement of a partial state. In the calculation of a state transition matrix, which is required to solve a differential equation, large rounding errors may occur when the time-step size is excessively small. To overcome this limitation, we introduce a precise integration algorithm to solve the differential equation. This algorithm is always numerically stable and yields very high precision solutions for numerical integration problems. To demonstrate the effectiveness of the proposed control strategy, we investigated the undamped vibration of a three-story building subjected to horizontal seismic forces. We assumed that the columns of the building are massless and that the mass of the structure is concentrated at floor levels. We implemented control using actuators exerting forces on each story. We also assumed that floor velocities can be measured in real time by sensors installed in every story unit. We used the NS component of the 1940 El Centro earthquake ground acceleration record as the excitation source and performed calculations for its entire duration. We modeled the columns of the building as linear elastic springs and assumed the response mitigation effect of the actuators to be sufficient for the building to behave in a linear elastic manner during earthquake excitation. We did not consider the soil-structure interaction or the dynamic characteristics of the actuators. We investigated the controlled and uncontrolled behavior of the three-story undamped building and compared the relative displacement, velocity, acceleration, and inter-story displacement responses. Our numerical simulation results show that the proposed closed/open-loop sub-optimal output feedback control strategy can significantly reduce structural earthquake responses.

Key words：earthquake excitation; output feedback; close/open-loop control; Kalman filter; precise integration

DOI:10.3969/j.issn.1000-0844.2015.04.0933

中图分类号:TU352.1

文献标志码：A

文章编号:1000-0844(2015)04-0933-05

作者简介：宋刚(1980-)，男，河南镇平人，博士，副研究员，主要从事结构振动控制及安全监测研究。E-mail: gangsong2008@163.com。

基金项目：交通运输部应用基础研究项目(2013319740080, 2014319740160)；交通运输部信息化技术研究项目(2013364740600)；重庆市科技人才培养计划项目(cstc2013kjrc-qnrc30001)

收稿日期：①2014-08-20