树枝形铁路专用线取送车作业模型及启发式算法



树枝形铁路专用线取送车作业模型及启发式算法

郭垂江，雷定猷

(中南大学 交通运输工程学院，湖南 长沙 410075)

摘要:合理安排铁路专用线取送车顺序，有利于提高调车机车作业效率、加速货车周转。以调车机车完成一批调车作业任务后所走行路程最短为优化目标；为便于区分，增设虚拟车站，并以各装卸作业点和车站为顶点；以根据作业情况不同调整后的作业点间距离为线段权，建立树枝形专用线取送车作业的哈密尔顿图模型，指出合理的取送车顺序为满足所有优先权关系的哈密尔顿回路。设计启发式算法进行求解，以不同作业的起点为始点，顺或逆时针确定机车下一访问作业点，从而形成不同的初始解，采用局部交换作业顺序规则对目前解进行改进，选择机车走行路程最短的路径为满意解。其他作业形式可认为是送调取结合作业形式的简化形式，所提出的模型及算法同样适用。

关键词：铁路；树枝形专用线；取送车；启发式算法

合理安排铁路专用线取送车顺序，有利于提高调车机车作业效率、加速货车周转。专用线按其线路的布置形式不同通常可分为放射形和树枝形两大类。放射形专用线取送车作业时向一作业点取送完车组后必须返回车站才能再去另一作业点取送车，各线车辆入线时刻不同，取回站内时刻也不同。树枝形专用线在一批作业中间不必返回车站，各线车辆入线时刻不同，但取回站内时刻相同。

1问题描述

取送车作业模式有单一送车、单一取车、送取结合、送兼调移、取兼调移和送调取结合。单一送车是指调车机车将需装卸的车组逐一送到相应的作业点，然后返回车站。单一取车是指调车机车将装卸完毕的车组逐一取回车站。送取结合简称“连送带取”，指在向各作业点送车的同时取回装卸完毕车辆。送兼调移是指将需装卸的车组送到相应地装卸地点，同时完成车组在作业点间的调移。取兼调移机车去专用线作业点取出装卸完毕的车组，同时完成车辆调移任务。送调取结合作业比较复杂，是指需送车的车组送到相应的装卸点、取出装卸完毕的车组，在取送车的同时完成车组在作业点间的调移。相关学者对铁路专用线取送车问题进行了一定的研究。石红国等[1-3]以机车在作业点间走行时间最小为优化目标，建立了树枝形铁路专用线取送车问题的哈密尔顿图模型，应用2-交换、最小生成树算法进行求解。雷友诚等[4-9]以完成一批作业任务的机车走行时间最小为优化目标，建立了相应的数学模型，采用遗传算法、蚁群算法进行求解。以上研究只适应于单一取车、单一取出等简单作业形式，难以适应铁路现场复杂的组合作业形式。郭垂江等[11]把树枝形专用线取(送)车作业优化问题转换成哈密尔顿图最短路问题，并松弛为指派问题，采用匈牙利算法得到最短回路路长的下界或最优解。若未得到最优解，再利用破圈连接法求出满意的取(送)车顺序，然后将模型扩展到其他作业形式。另外封全喜等[12]对物流配送车辆径路问题进行了深入研究，为本文研究提供了很好的借鉴。

本文讨论铁路车站树枝形专用线的取送车问题：即如何优化调车机车运用，使其在完成一批专用线的取送作业后所走行的路程最短。主要研究送调取结合作业形式，其他作业形式可认为是送调取结合作业形式的简化形式。下面结合一个典型案例说明整个模型建立及求解过程。

2模型建立

图1为一车站专用线布置图，v1为车站，v2，v3，…，v11为货物装卸作业点，数字为道岔岔心与作业点(车站)间实际路程。车站配备1台调车机车负责专用线的取送车作业，一批调车作业的作业任务如表1第1和第2列所示。

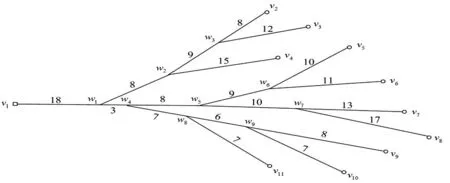
图1　树枝形专用线布置图Fig.1 Layout of branch-shaped railway siding

把问题构造成完备图G=[V,A,C]，如图2，V={v0,v1,...,v11}，v0为增设的虚拟车站，v1为铁路车站，vi(i=2,3,...,11)为货物作业点；A={(vi,vj)|vi,vj∈V}，(vi,vj)为连接作业点(车站)间的边；C={lij|i,j=0,1,2,...,11}，lij为机车在作业点(车站)间的机车走行距离, 规定l01=l10=0。

图2　哈密尔顿图Fig.2 Hamilton graph

若调车机车把车站v1的车组送往作业点vk，则调车机车必须先在车站v1连挂车组，然后才能送往作业点vk，即机车访问优先权为v1φvk(φ表示优先于)。

若作业点vi至作业点vj调移车组，则调车机车必须先在作业点vi连挂车组，然后才能送往作业点vj，即机车访问优先权为viφvj。

考虑作业点需同时取送的特殊情况，即假设需往把车站v1向作业点vi送车进行装(卸)，同时需把作业点vi装(卸)完毕的车辆取回车站v1。即存在优先关系为：v1φvi，viφv1。为避免以上矛盾，增加虚拟车站v0，则以上必须满足的优先关系为：v1φvi，viφv0。

若调车机车把作业点vl的车组取回车站v1，则调车机车必须先在作业点vl连挂车组，然后才能送往车站v1，即机车访问优先权为vlφv1。为与作业点需同时取送的分析统一，机车访问优先权记为vlφv0。

通过以上分析，调车机车要完成所有的取送车及调移任务，必须满足相应的优先关系。上例作业任务必须满足的优先关系如表1中的第4列。

将车站v1视作哈密尔顿图的出发顶点，每1个作业点看作1个需要经过1次的哈密尔顿图顶点，如果找到恰好经过各点并满足以上所有优先关系并回到车站v1的1条回路，就得到1个可行的取送车作业方案。哈密尔顿回路的路长为机车在各线段上机车走行距离lij的加总，总走行距离最短的可行哈密尔顿回路即为最优的取送车顺序。

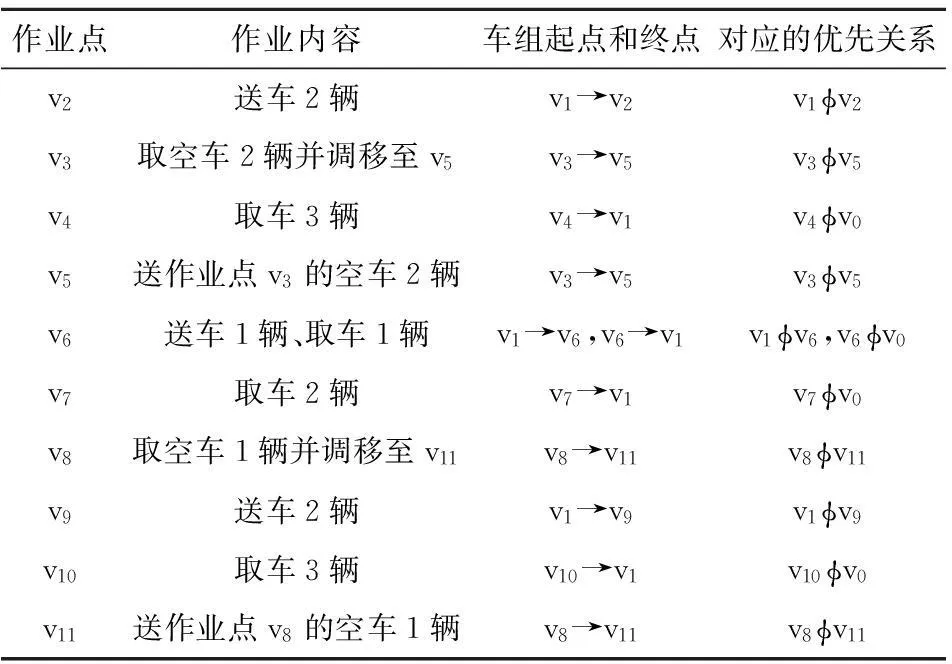
表1　取送调车作业任务

3机车走行路程的讨论

因为树枝形专用线所有的装卸线为尽头线，摘下连挂在机车上的车组时，必须保证所摘下的车组处在最外方位置。在取送车作业过程中，需进行调整车组的顺序，以便能摘下车组，因此机车在两作业点的距离lij不能简单地认为是线段之间的实际距离之和，可能因实际作业情况不同而需进行调整。下面对取送车作业存在的作业情况进行分析。

3.1取后送(送后取)

如图3，现假设调车机车需连挂若干车组从作业点vk将一车组取出后，再将另一车组送往作业点vi。

第1种作业情况机车的作业过程为：调车机车推送车组至作业点vk，连挂需取出的车组，牵出至点a，推进运行至作业点vj所在的装卸线，在警冲标e处停车，在需摘下的车组前摘钩后，牵引运行至点c，推送进入作业点vi所在的装卸线，至vi处摘下车组，牵引剩余的车辆至点c，转线至e处连接已停放的车辆，牵出过点a。

第2种作业情况机车的作业过程为：调车机车推送车组在警冲标b处停车，单机(也可能连挂着若干车辆)去作业点vk取出车组后，返回b处连挂原来放置的车辆，推送至作业点vi，摘下相应的车组后返回点a。

虽然调车机车需在两道岔区往返走行，但其走行距离相对货物线长度是很短的，所以完成该作业任务的机车走行距离可近似为2(l1+l2+l3)。相应地，图3中vi至点vk的机车走行距离可认为是l2+l1+l3。

按以上方法对先送后取作业进行分析，可得出同样的结论。

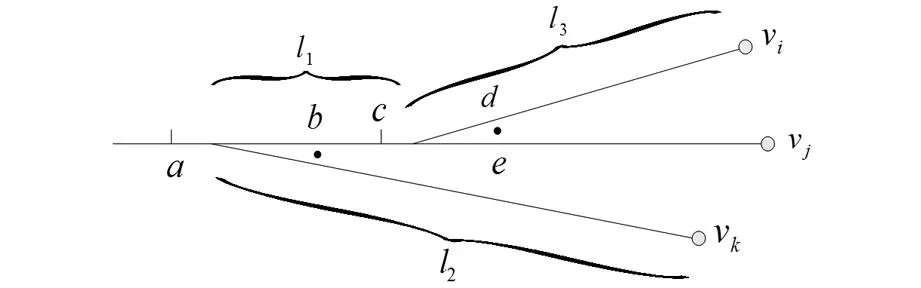
图3　取后送(送后取)作业过程分析图Fig.3 Process analysis of wagons’ placing-in after it’s taking-out (taking-out after it’s placing-in)

3.2调移

调移车辆就是调机往一个作业点的取出卸空的车组，然后送往另一作业点进行装车。一次调移作业可认为是一次取车作业和一次送车作业的结合。如图4，假设调车机车需从作业点vi调移空车至作业点vk，不失一般性，调移过程中还要执行其它作业任务(假设是向vj点送车)。机车的作业过程为：调车机车推送车辆过警冲标处e点后停轮，选择合适的车辆位置摘钩，牵引车组(或单机)至点a，然后推送至点vi连挂需调移的空车，牵引返回至点a转线至点e连挂原来放置的车辆，执行vj点送车任务，完成后牵引至点c，送作业点vi的空车至作业点vk，然后牵引返回点a。可以看出，由于需保证车组能顺利摘下，机车走行过程中须在道岔周围折返，但机车在岔区的走行距离相对货物线长度是比较短的，所以调车机车执行此次调移任务的走行路程可近似为2(l1+l2+l3+l4)。相应地，图4中vi至点vk的机车走行距离可认为是l2+l1+l4。

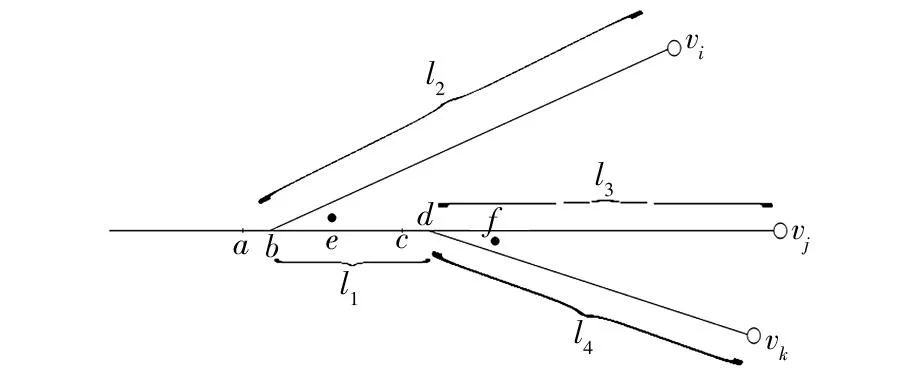
图4　调移作业过程分析图Fig.4 Process analysis graph of transferring operation

3.3作业点连送带取

现假设在向作业点vi送车的同时，取出已经装卸完毕的车组如图5所示。作业点连送带取在实际工作中存在2种情况：一是机车将车组送到作业点vi后，等待车组装(卸)完后再将其取出，机车需在作业点vi前等待；二是机车将车组送到作业点vi后，取出其他已装(卸)完毕的车组，此种情况机车需越线调车。显然，第1种情况不会增加机车的走行路程，只会增加机车的作业时间。下面对第2种作业情况进行深入分析。

机车的作业过程为：首先机车推送车辆过警冲标c，在合适的位置摘钩后，牵引部分车辆至点a，转线去作业点vi连挂装卸完毕的车组，返回点a，推送至点c与原来摘下的车辆连挂，在合适的位置摘钩(使要送的车组露出)，牵引运行至点a，推送运行至作业点vi，摘下车组后返回点a，推送运行至点c与原来摘下的车辆连挂。由于要保证车组能顺利摘下，机车须在道岔区折返，但其走行距离相对货物线长度是很短的，所以机车完成该作业任务的走行距离可近似为4l1。因此在构造机车走行

距离矩阵时，须相应地在点vi所在行、列中增加长度l1。如表1作业任务中因作业点v6需连送带取作业，本案例认为机车连送带取属于第2种情况，因此构造机车走行距离矩阵时，需在v6所在的行和列上分别增加11。

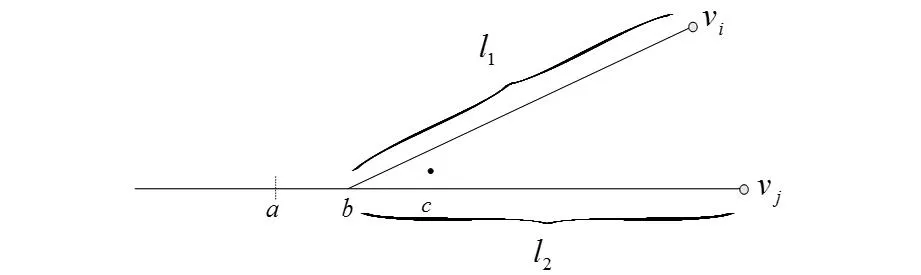
图5　作业点连取带送作业过程分析图Fig.5 Operation process analysis graph of wagons’ placing-in combined with taking-out in the same site

因为哈密尔顿图所有顶点没有环，最短路径问题为极小化问题，所以可令机车点间走行距离lii=M(i=0,1,…,11，M是足够大的正数)。表1案例设置M=80。

综上，得到表1案例的作业点间机车走行路程系数如表2。

表2　车站作业点(车站、虚车站)间机车走行路程

4启发式算法

为得到满意的取送车方案，设计以下启发式算法对模型进行求解[13-16]，计算步骤如下：

Step1 不区分作业任务的始点和终点，通过最小生成树的方法(MST)构造一个通过n+1个顶点的最小生成树T0；

Step2 选择任何一个作业任务的起点作为出发点，顺时针访问所有的作业点，最后返回v0。访问时按以下两个原则选择即将访问点。①以前访问过的作业点不访问；②任何起点还未访问的终点不访问。可得到的路径T1；

Step3 按下文所述的方法进行局部交换作业顺序，改进路径T1；

Step4 逆时针重复Step2和Step3,选择最短距离的路径T1；

局部交换作业顺序规则如图6，i，j，k，m为相邻作业点，在满足dij+dkm-dik-djm>0且点k不是一个起点为j的作业任务终点的条件下，图6(b)要优于图6(a)。需要说明的是，必须以上条件都满足的条件下才能交换，第1个条件能使机车走行距离缩短；第2个条件能保证路径的合法性。

图6　局部位置交换图Fig.6 Local position exchange graph

在计算表1案例时，首先利用避圈法得到图2的最小生成树如图7。

图7　最小生成树Fig.7 Minimum spanning tree

执行步骤2。如选择作业任务v3→v5的起点v3作为出发点，顺时针访问所有的作业点，最后返回点v0，得到可行的取送车顺序T1为：v1→v3→v4→v5→v6→v7→v8→v9→v10→v11→v2→v0，路程长为428。执行Step3局部交换作业顺序，如交换T1中的v6，v7位置，l56+l78-l57-l68=-38<0，说明交换不能改进路径。同样地交换T1其它所有相邻作业点，均不能改进径路。其他的方案计算可借助计算机进行。

利用MATLAB 7.0 编制程序，利用本文提出的启发式算法得到的满意解为：v1→v4→v2→v3→v8→v7→v5→v6→v11→v10→v9→v0，路长为：396。另利用穷举法得到最优解为：v1→v4→v2→v3→v5→v6→v7→v8→v9→v10→v11→v0，路长为：394。本文的案例与参考文献[11]的案例是相同的，文献[11]得到的满意解为：v1→v10→v7→v8→v3→v2→v11→v5→v6→v9→v4→v0(因标号不同，表达方式与原文有差异)，总路长为472。可见，本文所设计的启发式算法是比较优越的。

5结论

1)若要以机车走行时间最少为优化目标，因机车在调车过程中要进行转线、对位等作业，需多次在线路上加减速，因此计算时要对各项作业时间进行严格查定，方可适应要求。

2)本文的启发式算法中的局部交换是采用2-交换的方法进行的，还可以采用3-交换、k-交换等方法，但一定要保证交换后取送车顺序的有效性。

参考文献：

[1] 石红国，彭其渊，郭寒英.树枝型专用线取送车问题的哈密尔顿图解法[J].中国铁道科学，2005，26(2):132-135.

SHI Hongguo, PENG Qiyuan, GUO Hanying. An algorithm by using Hamilton graph to resolve wagons placing-in and taking-out on branch-shaped sidings[J]. Chian Railway Science,2005,26(2):132-135.

[2] 王慈光.运输模型及优化[M].1版.北京:中国铁道出版社,2004.

WANG Ciguang. Transport model and optimization[M].1st Edition. Beijing:China Railway Publishing House,2004.

[3] 黄向荣.树枝形专用线取送车的模型及算法研究[J].兰州交通大学学报，2007，26(3): 51-54.

HUANG Xiangrong. Model of wagons placing-in and taking-out on branch-shaped sidings and the calculating method [J].Journal of Lanzhou Jiaotong University(Natural Sciences),2007,26(3): 51-54.

[4] 雷友诚,涂祖耀,桂卫华，等.基于遗传蚁群算法的树枝型铁路取送车问题优化[J].中南大学学报(自然科学版)，2011，48(2):2356-2361.

LEI Youcheng, TU Zuyao, GUI Weihua, et al. Optimization of placing-in and taking-out wagons on branch-shaped railway lines based on genetic and ant colony algorithm[J].Journal of Central South University(Science and Technology) ,2011,48(2):2356-2361.

[5] 杨运贵,王慈光,薛锋.树枝形铁路专用线取送车问题的遗传算法研究[J].计算机工程与应用，2008，44(12):210-211.

YAN Yungui, WANG Ciguang, XUE Feng. Study on genetic algorithm for railway placing-in and taking-out of wagons in branch-shaped private siding[J].Computer Engineering and Applications,2008,44(12):210-211．

[6] 李海军，朱昌锋.放射形铁路专用线直达车流取送车问题的单亲遗传算法研究[J].铁道科学与工程学报，2011,8(6)：114-117.

LI Haijun, ZHU Changfeng. Study of through wagon flow on single-parent genetic algorithm for railway placing-in and taking-out of wagons in atinoid private line[J].Journal of Railway Science and Engineering，2011,8(6)：114-117.

[7] 王雅琳，李开峰，马杰，等．遗传算法在企业铁路取送调车作业优化中的应用[J]．系统工程．2007，25(3)：94-99.

WANG Yalin, LI Kaifeng, MA Jie, et al. Application of genetic algorithm to optimal for placing-in and taking-out of wagons at enterprise[J]. Systems Engineering, 2007，25(3)：94-99.

[8] 李智.基于改进型蚁群算法的货物作业车取送模型优化[J].铁道运输与经济，2004，26(4)：73-76.

LI Zhi．Optimization of placing-in apd taking-out wagon operation model based on enhanced ant colony algorithm[J]．Railway Transport and Economy，2004，26(4)：73-76．

[9] 李斌，董昱，孙云霞.树枝形专用线取送车优化问题的研究[J].郑州大学学报(工学版)，2014，35(1):20-24.

LI Bin, DONG Yu, SUN Yun-xia. Research on PTW on branch-shaped sidings[J].Journal of Zhengzhou University (Engineering Science), 2014，35(1):20-24.

[10] 邓连波，史峰，莫辉辉.物流配送车辆路径问题多代竞争遗传算法[J].铁道科学与工程学报，2005,2(5)：75-79.

DENG Lianbo, SHI Feng, MO Huihui. Multi-generation compete genetic algorithms for logistics distribution vehicle routing problem. [J].Journal of Railway Science and Engineering，2005,2(5)：75-79.

[11] 郭垂江，雷定猷.树枝形专用线取送车问题哈密尔顿图模型及算法[J].交通运输系统工程与信息，2014,14(3)：105-109.

GUO Chuijiang, LEI Dingyou. Hamilton model and algorithm for placing-in and taking-out wagon problem on branch-shaped siding[J].Journal of Transportation Systems Engineering and Information Technology, 2014,14(3):105-109.

[12] 封全喜，刘诚.物流配送车辆路径问题的并行遗传算法研究[J].铁道科学与工程学报，2005,2(4)：88-91.

FENG Quanxi, LIU Cheng. The study of parallel genetic algorithm for vehicle routing problem of logistic distribution[J].Journal of Railway Science and Engineering，2005,2(4):88-91.

[13] Renaud M, Stefan R, Fabien L, et al. A branch-and-cut-and-price approach for the pickup and delivery problem with shuttle routes[J]. European Journal of Operational Research, 2014(236):849-862.

[14] Rais A, Alvelos F, Carvalho S M. New mixed integer-programming model for the pickup-and-delivery problem with transshipment[J]. European Journal of Operational Research, 2014,235(3):530-539.

[15] Rego C, Gamboa D, Glover F, et al. Traveling salesman problem heuristics: Leading methods, implementations and latest advances[J]. European Journal of Operational Research, 2011,211(3):427-441.

[16] Jacques R. A heuristic for the pickup and delivery traveling salesman problem[J]. Computers & Operations Research, 2000(27)：905-916.

Wagons' placing-in and taking-out model in branch-shaped

railway and its heuristic algorithm

GUO Chuijiang, LEI Dingyou

(School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China)

Abstract:Reasonable arrangement on sequence of wagons' placing-in and taking-out in railway siding is beneficial to improve the efficiency of shunting locomotive, and is conductive to accelerate wagons turnover. It was taken as an objective to minimize the locomotive's running distance after completing a series of shunting operations. In order to distinguish them with ease, virtual stations were added. Taking loading and unloading sites and stations as vertices, and considering the adjusted distance between operation sites according to different operation situations as weights, the graph model of wagons' placing-in and taking-out in branch-shaped railway siding was formulated. Rational placing-in and taking-out sequences were Hamilton loops which satisfy all priorities. A heuristic algorithm was designed to solve it. Taking origination of different operation as the starting point, different initial solutions were formulated through determining the next operating point according to clockwise or counterclockwise direction. The current solutions were improved with local exchange rules, and the route with shortest distance was selected as the satisfied solution. Other forms could be considered as simplified forms of wagons' placing-in, taking-out and transferring combination. The model and algorithm proposed in this paper are also applicable for them.

Key words:railway; branch-shaped railway siding; wagons' placing-in and taking-out; heuristic algorithm

中图分类号：U292.13

文献标志码：A

文章编号：1672-7029(2015)01-0208-06

通讯作者：郭垂江(1980-)，湖南武冈人，博士研究生，从事车站运输组织优化研究；E-mail: guochuijiang@sina.com

*收稿日期：2014-07-25