GPS高程异常拟合粗差剔除以及精度评价方法研究



GPS高程异常拟合粗差剔除以及精度评价方法研究

李浩，吴祖海

(中南大学 土木工程学院，湖南 长沙 410075)

摘要:提出一种GPS高程拟合公共点粗差定位的新方法，即利用最小二乘法平差所得方差，采用假设检验法，完成GPS高程异常拟合模型参数计算过程中的粗差定位与剔除。对多种高程拟合模型的拟合精度进行评价，引入均方误差、信噪比和互相关系数评价指标，提出一种多指标融合评价方法，实现对GPS高程异常拟合精度的评价。结合实例分析，证明所提方法的有效性。

关键词：GPS高程异常；拟合模型；粗差定位；精度评价

GPS测量参照的坐标系是WGS-84地心坐标系，其测得高程是相对于WGS-84椭球的大地高，记为H。它是一个几何量，没有物理意义[1]。我国在实际工程中应用的坐标系统一般采用似大地水准面为基准，其高程称为正常高h。这两者存在高程异常ξ，可以用式ξ=H-h来表达这两者之间的关系。由此式可以得出，若某点的高程异常值已知，那么可以将该点的GPS高程转换成实际工程中所需要的正常高。目前计算高程异常的方法主要有重力测量法[2]、数值逼近法[3]、联合平差法[4]和神经网络法[5]等，在实际工程中运用最多的是数值逼近法，其中二次曲面拟合法[6]最普及。运用该法求解转换系数时，若没有考虑所给公共点自身的误差，强制进行转换，会产生错误的拟合结果。对于含有粗差的数据处理一般分为2种方法：将粗差归入函数模型或将粗差归入随机模型[7]。选择适当的权函数，消除或者削弱粗差对参数估计的影响，这一类方法的困难在于合理权函数的选择，抗差的严密精度有待进一步研究。上述方法主要通过最小二乘计算得到的改正数V来判定粗差，但根据理论含有粗差的公共点改正数不一定会大，所以会造成粗差误判的情形。本文提出一种新方法，利用最小二乘平差后的方差构建统计量，克服了常规粗差定位中使用改正数V容易掩盖粗差的缺点，实现了GPS高程拟合参数计算过程中已知点的粗差定位和剔除。GPS高程拟合可以通过2方面来评定其精度。一方面是内符合精度，另一方面是外符合精度[8]。以上这2个指标虽然能得到正确的结论，但在具体选择某一种高程拟合方法时，还必须考虑更多的评价指标，让模型选择更加可靠。为了使GPS高程拟合模型更具有说服力，本文将均方根误差、信噪比、互相关系数[9]纳入GPS高程拟合精度评价，并提出一种多指标融合评价方法。最后结合实例证明所提方法的有效性。

1粗差探测F检验法

1.1二次曲面拟合模型

二次曲面拟合法在GPS高程异常拟合中应用非常广泛，其主要原理是建立GPS高程异常的数学模型，利用已知点(同时具有大地高H和正常高h)进行参数拟合，再利用拟合好的数学模型求解其他GPS点的水准高程。在平坦地区，GPS高程异常值的拟合采用二次曲面拟合模型效果较好。二次曲面拟合的数学模型[6]为

ξ(x,y)=a0+a1x+a2y+a3x2+a4xy+a5y2

式中，x和y为GPS点的点位坐标。

上式模型可以简化成矩阵形式：

设V为高程异常的改正数，ξ0为二等水准联测已知点高程异常的理论值。则高程异常数学模型的误差方程为

其中V=ξ-ξ0。

则拟合参数的估值为

式中：n为已知点的个数，t为必要观测数。

1.2F检验法原理

下面以二次曲面拟合为例，说明拟合模型正确性的统计检验方法，流程如下。

(1)利用所有的已知点，构成误差方程：

(3)原假设和备用假设为

统计量为

该统计量服从F分布[11]，即Fi～F1-α(r1,r2)，故采用F检验法。选取α，以自由度r1,r2查得F1-α(r1,r2)，得到区间[0,F1-α(r1,r2)]，若统计量不在此区间内，则拒绝H0，认为该点存在粗差。若数据含有多个粗差，这些粗差会相互影响，造成粗差误判的情况。针对这种情况，可以采取每一轮只剔除粗差最明显的那个点，然后开始下一轮的检验，直到所有粗差被剔除。

2GPS高程异常值拟合精度多指标融合评价方法

2.1传统精度分析方法

2.1.1内符精度[8]

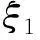
式中：n为参与计算的已知点数。

2.1.2外符精度[8]

外符合精度和内符合精度的原理是一样的，只不过是用于计算异常值差值的已知数据不同，外符合精度通过计算检测点的观测高程异常值和用于拟合之外检核点的高程异常值之间的差值获得。GPS高程拟合的外符合精度M的计算公式如下所示：

式中：n为参与检核的点数。

内符合精度以及外符合精度从某种意义上来讲其实是一种相对意义上的绝对精度评定。

2.2多指标引入精度分析

2.2.1均方根误差

均方根误差[12]是指拟合后的高程异常值ξ1与二等水准联测所得到的高程异常值ξ0的均方误差，简称RMSE。

均方根误差体现了拟合高程异常值与观测高程异常值之间的差异，在实际应用中，均方误差越小表示该模型拟合效果越好。

2.2.2信噪比

信噪比[12]是指原始观测高程异常信号能量与噪声能量的比值，简称SNR。

一般认为，信噪比越高，表示该模型拟合效果越好。

2.2.3互相关系数

互相关系数[13]指拟合后的高程异常值ξ1(i)与原始观测高程异常值ξ0(i)的相似度，记为R。

R越接近1，表示该模型拟合效果越好。

2.3多指标融合评价方法

多指标融合评价法综合考虑均方根误差、信噪比以及互相关系数等度量指标，将所有指标归化到[0,1]区间并求和，记为H，则：

H(M)=Pυ(M)+PSNR(M)+PR(M)

Pυ(M)，PSNR(M)和PR(M)分别表示均方根误差、信噪比和互相关系数的归一化值。在实际应用中，多指标融合评价值H越大，则认为拟合效果越好。

3实例分析

3.1工程简介

某市区B级GPS网(平缓区域，区域面积约为10km2)共布设19个点,如图 1所示。GPS观测采用4台中纬ZGP800接收机进行，采用静态相对定位模式。出于研究目的，对各点均施测了二等水准，观测仪器为天宝DINI03电子水准仪。GPS网总共19个点的平差结果以及二等水准观测结果见表1。

图1　某市区B级GPS控制网Fig.1 B-order GPS network

3.2利用F检验法剔除粗差

根据前面的理论知识进行粗差探测，选取α=0.25[10]，求得的统计量见表2。

从表2中可以得出，第1轮检验时取F0.75(13,12)=1.486 2，可以探测到14号点为粗差点；第2轮检验时取F0.75(12,11)=1.514 0，可以探测到18号点是粗差点；第3轮检验时取F0.75(12,11)=1.546 9，发现所有检验量都在接受域之内，表明不存在粗差。

3.3多指标融合评价高程异常拟合效果

实际工程涉及到很多小范围的区域，而这些区域内存在河流、建筑物等等妨碍水准测量的障碍物，出于经济、效率、工期等因素的考虑，运用GPS测水准高程将变得非常有利。在拟合高程模型时往往需要很多已知点，但很多工程不可能提供非常详尽的数据，本文出于实际考虑，选取了某GPS试验网的高程拟合数据，分别用多面函数法、移动法、二次曲面拟合法对该控制网高程异常进行拟合，拟合结果见表3。

表1　B级GPS和二等水准观测结果

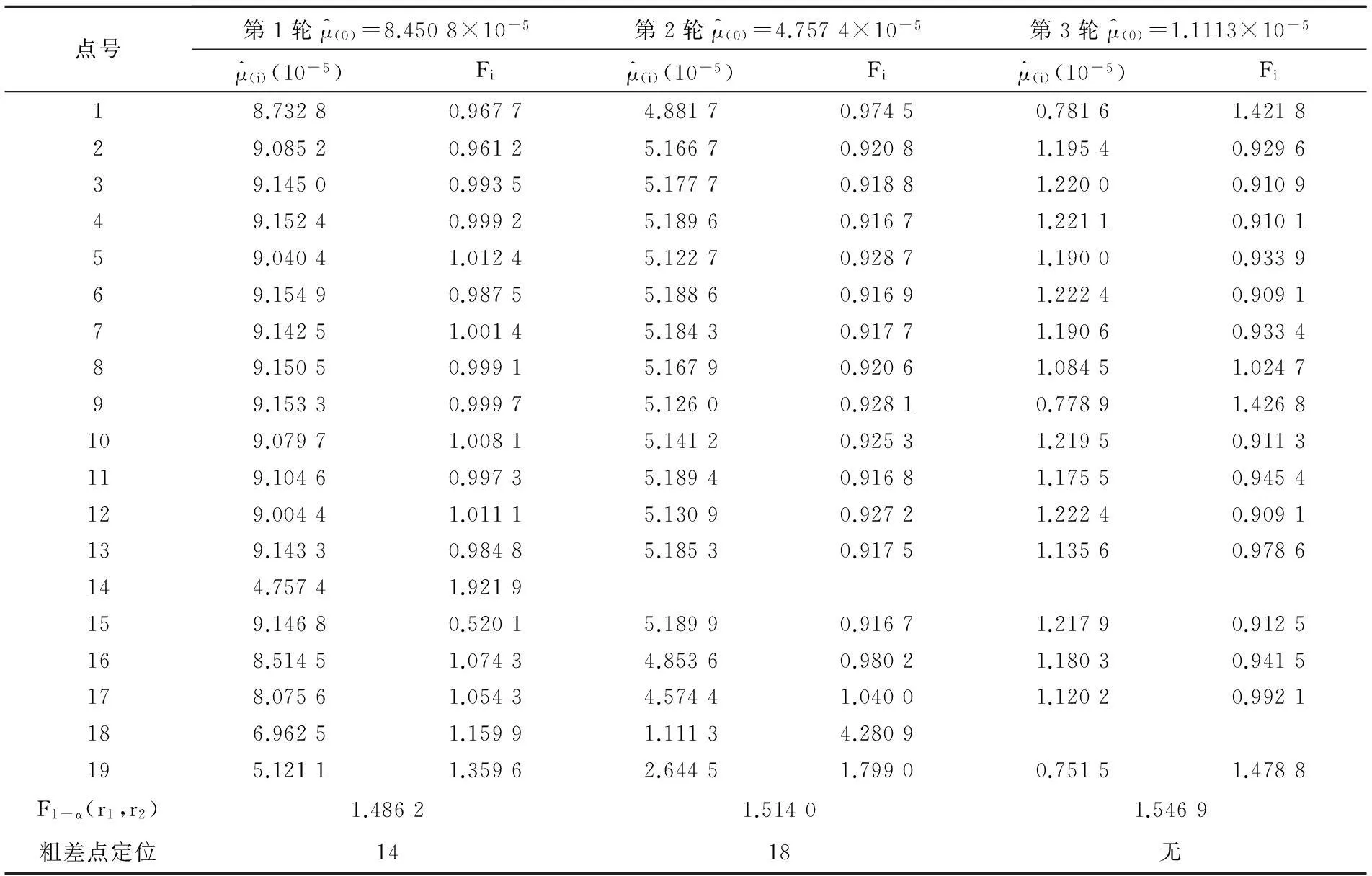
表2　粗差探测F检验法数据统计

表3　高程异常拟合结果

利用多指标融合评价方法，分别计算已知高程异常与拟合高程异常的均方误差、信噪比、互相关系数。然后根据计算数据比较内符精度、外符精度以及多指标融合精度的大小，依据计算结果选择最合适的拟合方法，计算结果见表4。

表4　不同指标下不同拟合方法拟合效果的评价结果

从表4可以得出，内符精度和外符精度都表明二次曲面拟合法拟合效果较好，而多指标融合评价法也得出了相同的结论，说明该评价方法是有效的。与此同时，多指标融合评价方法给出了具体的量化数值比较，更具有说服力和可靠性。

4结语

1)针对GPS高程异常二次曲面拟合法的粗差定位与剔除，提出了一种简单、可操作的F检验法，其能够准确定位原始数据中的粗差，能提高高程异常拟合精度；

2)研究了现有的GPS高程拟合精度评价方法，结合具体工程实例，将均方误差、信噪比、互相关系数引入高程异常拟合精度评价，提出多指标融合评价方法，使被选择的高程拟合方法更具有可靠性；

3)本文所提出的粗差探测方法是针对二次曲面拟合法，其他拟合方法的粗差剔除能否运用此检验法有待进一步的研究。同时，本文针对GPS高程拟合精度所提出的多指标融合评价方法不局限于此，在其他方面的运用更值得深入探讨。

参考文献：

[1] 徐绍铨，李振洪，吴云孙. GPS高程拟合系统的研究[J]. 武汉测绘科技大学学报,1999,24(4):336-340.

XU Shaoquan, LI Zhenhong, WU Yunsun. Research of GPS abnormal height interpolation system[J].Journal of Wuhan Technical University of Surveying and Mapping,1999,24(4): 336-340.

[2] 陆彩萍，伍吉仓，王解先.顾及EGM96模型的GPS水准高程拟合[J]. 测绘工程,2002,11(3):31-34.

LU Caiping,WU Jicang,WANG Jiexian.The GPS/level height fitting considering of EGM96[J].Engineering of Surveying and Mapping,2002,11(3):31-34.

[3] 金时华.多面函数拟合法转换GPS高程[J]. 测绘与空间地理信息,2005,28(6):44-47.

JIN Shihua. GPS height transformation using hardy function interpolation method[J].Geomatics & Spatial Information Technology,2005,28(6):44-47.

[4] Mikhail E M, Ackermann F. Observations and least squares[M].New York,1973.

[5] 杨明清，靳蕃，朱达成，等.用神经网络方法转换GPS高程[J]. 测绘学报,1999,28(4):301-307.

YANG Mingqing, JIN Fan, ZHU Dacheng, et al. Conversion of GPS height by artificial neural network method[J]. Acta Geodaetica et Cartographica Sinica,1999,28(4):301-307.

[6] 王解先.工业测量中一种二次曲面的拟合方法[J]. 武汉大学学报(信息科学版),2007,32(1):47-50.

WANG Jiexian. A method for fitting of conicoid in industrial measurement[J]. Geomatics and Information Science of Wuhan University,2007,32(1):47-50.

[7] Huber P J.Robust statistics[M].New York:Wiley,1981.

[8] CHEN Junping, WANG Jiexian. The conic fitting in engineering surveying[J].Geotechnical Investigation and Surveying,2003(5):59-61.

[9] 陶珂，朱建军.小波去噪质量评价方法的对比研究[J]. 大地测量与地球动力学,2012,32(2):128-133.

TAO Ke, ZHU Jianjun. A comparative study on validity assessment of wavelet de-noising[J].Journal of Geodesy and Geodynamics,2012,32(2):128-133.

[10] 吴祖海，罗伟钊，李军.坐标转换中公共点粗差定位与降低粗差点影响方法研究[J]. 大地测量与地球动力学,2014,34(1):118-122.

WU Zuhai, LUO Weizhao, LI Jun. On position of gross errors of common points in coordinate transformation and reducing influence of gross errors[J]. Journal of Geodesy and Geodynamics,2014,34(1):118-122.

[11] 陶本藻.测量数据处理的统计理论和方法[M].北京:测绘出版社,2007.

TAO Benzao. Statistic theory and method of surveying data processing[M].Beijing: Surveying and Mapping Press,2007.

[12] 文鸿雁.基于小波理论的变形分析模型研究[D].武汉：武汉大学，2004.

WEN Hongyan. A study of deformation analysis model based on wavelet theory[D].Wuhan:Wuhan University,2004.

[13] 陈强，黄声享，王韦. 小波去噪效果评价的另一指标[J]. 测绘信息与工程,2008,33(5):13-14.

CHEN Qiang, HUANG Shengxiang, WANG Wei. an evaluation indicator of wavelet de-noising[J].Journal of Geomatics,2008,33(5):13-14.

Research on removed GPS elevation based on abnormal fitting

gross errors and accuracy evaluation methods

LI Hao, WU Zuhai

(School of Civil Engineering, Central South University, Changsha 410075, China)

Abstract:A novel method was presented in this paper where variance after least square adjustment was used to locate the gross errors in the calculation of GPS elevation fitting model parameters using hypothesis testing. The accuracy of different elevation fitting models was evaluated by introducing evaluation index of mean square error, signal-to-noise ratio, mutual correlation coefficient, and a hybrid evaluation method was proposed to assess the accuracy of GPS elevation anomaly fitting. Combined with some practical projects, the results calculated in this literature prove that these methods are valid.

Key words:GPS height anomaly; fitting model; gross error locating; accuracy evaluation

中图分类号：P228

文献标志码：A

文章编号：1672-7029(2015)01-0099-06

通讯作者：吴祖海(1956-)，男，湖南长沙人，副教授，从事精密工程测量教学与科研工作；E-mail：xic18@163.com

基金项目：国家自然科学基金资助项目(41171326)

*收稿日期：2014-07-08