基于遗传单纯形算法与RBF网络的地应力场反演方法



基于遗传单纯形算法与RBF网络的地应力场反演方法

谢学斌1，罗海霞1，杨承祥2，李欣1

(1. 中南大学 资源与安全工程学院，湖南 长沙410083；

2. 安徽铜冠(庐江)矿业有限公司，安徽 铜陵 231561)

摘要:为提升RBF神经网络性能，采用遗传单纯形算法优化RBF神经网络隐含层节点中心值，利用FLAC3D软件建立区域的数值计算模型来进行正分析计算，以若干测点的正应力值作为训练样本，用优化的RBF网络反演模型区域的岩体力学参数及初始地应力场。依据沙溪铜矿区的地质资料进行算例分析，该方法的反演计算值、实测值及其他RBF网络反演计算值对比表明：所采用的遗传单纯形算法优化RBF网络的反演方法是可行的，改善了计算精度，对类似工程有一定的参考价值。

关键词：初始地应力场；反演；FLAC3D；遗传算法；单纯形算法；RBF神经网络

初始地应力场是岩石力学研究的重要内容，能确定工程岩体力学属性，当岩体所在环境条件改变时，也是导致变形及破坏的关键力源之一。工程设计与施工的可靠性与安全性研究往往取决于初始地应力场与岩体参数选取的合理程度。因此，初始地应力场和岩体力学参数的反演历来是岩石力学的重要课题之一[1-7]。地应力场反演主要有2种方法：一是根据现场实测的开挖位移资料进行反演[8]；二是根据工程区域某些实测地应力点，考虑地质、地形、岩性等，做相应的假定和简化，对初始地应力场进行反演。根据少数实测地应力点进行初始地应力反演的一般方法有：边界荷载调整法、应力函数趋势分析法、多元回归分析法[9]和现代智能方法等。其中，现代智能方法里应用最广的遗传算法和人工神经网络因其固有的鲁棒性、学习联想及推广能力和全局搜索能力等优点，成为解决极其复杂的岩土工程问题的有效方法。例如，夏江等[10-11]采用遗传算法对软土地基沉降进行预测，王树栋[12]利用进化的神经网络算法进行软岩位移反分析计算，张乐文等[13]利用径向基函数(Radial Basis Function，RBF)神经网络来反演初始地应力和岩体参数。

RBF神经网络是一种新型的局部逼近神经网络，与BP网络[14]相比较，该网络结构简单、非线性逼近能力强、训练简洁且学习时间短。但至今没有系统的方法来确定RBF网络的结构及参数(隐含层节点数、隐含层中心值、宽度及隐层至输出层的连接权值)。隐含层中心值的选取对RBF网络的函数逼近能力有很大的影响，不恰当地选取会引发网络收敛慢，甚至网络发散等情况。遗传单纯形算法是遗传算法与单纯形算法结合而成的混合算法，同时具备遗传算法简单通用、全局随机搜索及单纯形算法快速寻优、收敛的优点。因此，为进一步提升RBF网络性能，本文利用遗传单纯形算法对RBF网络隐含层中心值的选取进行优化，进而将基于遗传单纯形算法优化的RBF网络应用到地应力反演研究中。

1遗传单纯形算法优化RBF网络算法

1.1RBF网络的拓扑结构

RBF网络是一种3层前馈反向传播网络，拓扑结构为：第1层—输入层、第2层—隐含层和第3层—输出层(如图1)。

图1　RBF神经网络拓扑结构Fig.1 RBF neural network topology

将 RBF网络应用于地应力场反演中，则输入层单元Xi(i=1,2,3)代表测点的三大主应力值，隐层执行的非线性变换是固定不变的，输出层yi(i=1-5)则表示岩体力学参数及侧压力系数，其输出节点的计算是根据隐节点的径向基函数的线性组合。用实测点的主应力数据作为反馈信号，并按一定的学习算法，利用三维地质模型计算出的数据样本训练RBF网络，让不同的输入向量得出不同的输出向量，若某时计算输出值和反馈信号的误差小于一定的允许值，则训练结束。

RBF网络中最常用的非线性函数是高斯函数

(1)

1.2遗传单纯形算法的原理

遗传算法是一种求解问题的高效并行全局搜索方法，它通过对当前群体施加随机选择、交叉、变异等遗传操作，产生新一代的群体，并且逐步使群体进化到包含或者接近最优的状态。群体搜索策略及群体个体间的信息互换是遗传算法的主要特点。但其存在局部寻优能力较弱，易出现早熟收敛现象，搜索效率低等缺陷。

单纯形算法(Simplex Algorithm，SA)[15]，亦称为可变多面体搜索算法，是确定性下降方法，有很强的局部寻优能力。遗传单纯形算法(Genetic-Simplex Algorithm，GSA)[16]将2种算法有效地结合，利用遗传算法的基本框架做基础，遗传算法的交叉操作及变异操作替换为单纯形算法，提高了全局搜索和局部搜索的能力、效率，改善了遗传算法的缺陷。

1.3遗传单纯形算法优化RBF网络算法步骤

RBF网络隐含层中心值应能描述输入空间的分布性质，即在输入空间内中心值应均匀分布。中心值的选取适当是RBF网络发挥良好性能的前提。目前常用的RBF网络隐含层中心值确定方法都存在缺陷，最多只能得到中心值的次优解，如K-均值聚类法，受初始聚类中心值的影响，而遗传单纯形算法采用群体搜索策略，初始聚类中心对其影响不大，能达到全局最优，进而提高RBF网络性能。

遗传单纯形算法优化RBF网络隐层中心值的主要流程如下：

(1)编码。常用的编码方式有二进制编码和实数编码。实数编码可使问题表述更自然直观，简化了编码、解码过程，较易引入相关领域的启发信息，提高了算法的速度及精度。本文主要利用遗传单纯形算法优化径向基函数的中心值，涉及连续变量设计，且中心值的取值比较大，故采用实数编码方式。

(2)初始化种群。种群大小是遗传算法的一个重要参数。种群规模选择过大会增加计算的负担，收敛时间会大幅度增加；过小会降低个体多样性，易早熟，可能导致全局最优解搜索困难。

(3)适应度函数的构造。适应度函数作为遗传算法指导寻优搜索的关键指标之一。均方误差是衡量RBF网络性能的指标，结合网络复杂程度，本文选择基于AIC(Akaike’s information criterion)准则[17]的适应度函数：

f=-[Nlog(mse)+4k]+b

(2)

其中：mse为均方误差，表达式为：

(3)

式(2)～(3)中：N是输入向量样本个数；K是隐含层神经元个数；ti是神经网络的输出向量；ei是目标输出向量；b是待定系数(为保证f大于0，一般取较大的值)。

(4)遗传算法利用选择算子对群体中的个体进行优胜劣汰操作。

(5)选择个体构造单纯形，执行单纯形进化算子。

(6)找到最优种群，即RBF神经网络隐含层中心值。

遗传单纯形算法优化RBF网络的流程如图2所示。

2基于遗传单纯形算法优化的RBF网络的地应力反演步骤

利用遗传单纯形算法优化的RBF网络，进行地应力场的反演，主要步骤如下：

(1)确定待反演参数，并利用FLAC3D软件建立三维地质模型，获取训练样本。

(2)将训练样本进行归一化处理。

(3)构建RBF网络结构，确定RBF网络的目标函数及相关运行参数。

(4)确定遗传单纯形算法的遗传操作方法、适应度函数、遗传单纯形算子及相关运行参数。

(5)利用遗传单纯形算法进行搜索，寻优RBF网络隐层中心值，得到多个最优解。

(6)将最优解输入RBF网络，利用适应度值进行测评，筛选最优良的中心值，从而获得中心值最优解。

(7)优化后的RBF网络进行隐含层的无导师训练及输出层的有导师训练，建立地应力反演计算的非线性映射模式。

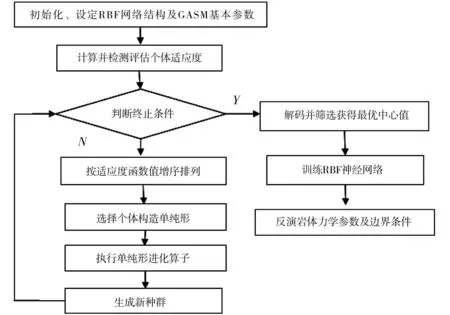
图2　遗传单纯形算法优化RBF神经网络的流程图Fig.2 Flow chart of RBF neural network optimized by GSA

(8)重新把检验样本作为输入样本代入优化的RBF网络，验证输出向量与工程实际是否相符。若不相符，则重复执行5-7步骤直至满足要求。

(9)将测点的地应力实测值作为输入样本代入第8步结果验证为符合的GSA—RBF网络模型，输出向量即是第1步确定的待反演参数。

(10)把第9步的反演参数代入FLAC3D地质模型进行正分析计算，可得到三维计算模型中任意点的地应力值。

3算例分析

3.1三维地质力学模型的建立

沙溪铜矿区为铜陵有色金属控股有限公司拟建矿山，由铜泉山矿段和凤台山矿段组成。在矿山开采设计进行岩石力学研究阶段，结合地质勘探钻孔工程取样，利用声发射进行了原岩应力场测量。本文以沙溪铜矿区实测地应力资料为基础，利用GSA—RBF网络，进行地应力场的反演。正分析过程中利用FLAC3D进行建模，最大程度地依据工程实际情况模拟地表，并适当简化断层破碎带及蚀变带。模型选取较大的模拟范围来减小“边界效应”的影响：X轴方向为近东西方向，模拟长度为2 000 m;Y轴方向与X轴方向垂直，模拟长度为2 000 m;Z轴正方向为铅直向上，模拟范围为0～1 230 m。三维地质力学模型的网格划分如图3所示，划分四面体和六面体等参单元总共17 277个。沙溪铜矿区岩性随深度变化，在模型模拟范围内从下至上大致分为A，B和C 3组，A组为石英闪长斑岩，B组为石英闪长玢岩，C组为泥质粉沙岩。

图3　三维地质模型Fig.3 3D geological model

3.2反演参数选取

FLAC3D正分析模型采用Mohr-Coulomb破坏准则，需要反演的岩体物理力学参数主要有：体积模量、泊松比、密度、剪切模量、凝聚力、内摩擦角、膨胀角和抗拉强度。普遍情况下，体积模量K，泊松比μ和密度ρ对初始地应力场影响较大。初始地应力场主要由自重应力场和构造应力场组成，而对于沙溪铜矿区这种深埋地质条件，构造应力场占很大比例，侧压力系数用λ表示。因此，待反演量主要有体积模量K，泊松比μ，密度ρ及侧压力系数λ。

3.3反演过程

第1步:正分析计算。

根据沙溪铜矿区情况，选取铜泉山矿段编号为TQ2和TQ3，凤台山矿段编号为FT1-1，FT1-2，FT2-1的5个测点，并沿用基于声发射方法的这5个点的实测地应力值。在正分析计算中，调整这5个点的18组不同的岩体力学参数及侧压力系数，将其代入已建好的地质力学模型进行相应正分析计算，得到对应的18组“实际测点”的主应力值。将获得的18组主应力值作为GSA—RBF网络的输入样本，18组岩体力学参数及侧压力系数作为GSA—RBF网络的输出样本。

第2步:归一化处理。

把学习样本按下式进行归一化处理，使样本数据位于区间[0,1]，如表1所示。限于篇幅，在此仅列出输出样本中地质力学模型第1，6，12，18和19组岩体力学参数中的体积模量K，泊松比μ，密度ρ及侧压力系数λ。

(4)

第3步：GSA—RBF网络模型构建。

将作为输入样本的主应力值按一定顺序排列、编码，选择初始种群规模为40，遗传进化的最大代数取150，选择操作按照随机遍历抽样法；子种群个数为3，单纯形顶点数为16，单纯形内循环次数为30；隐层神经元个数根据moody准则取为20个，权值采用伪逆法，中心基函数的宽度取相同的值。根据数据样本，按照式(1)求得对象函数值，再按照式(2)得到适应值，并作为网络性能评价的依据，得到的值输出给网络，网络依据新值前向计算得到新的输出，作用于反演系统。优化过程中群体目标函数的变化过程如图4所示。

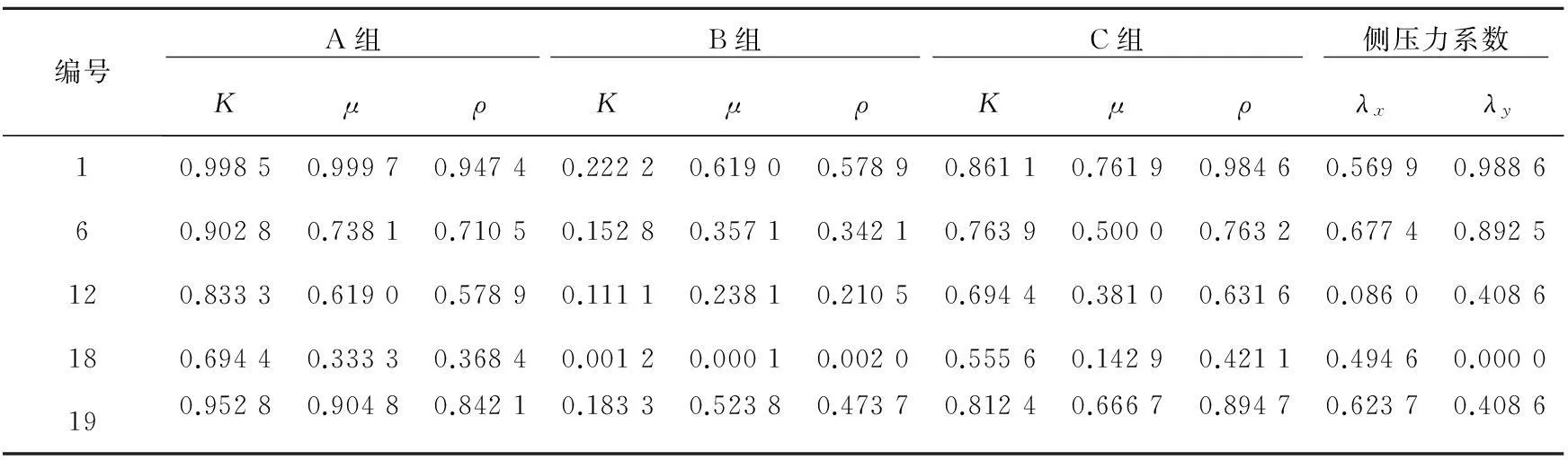
表1　反演参数归一化

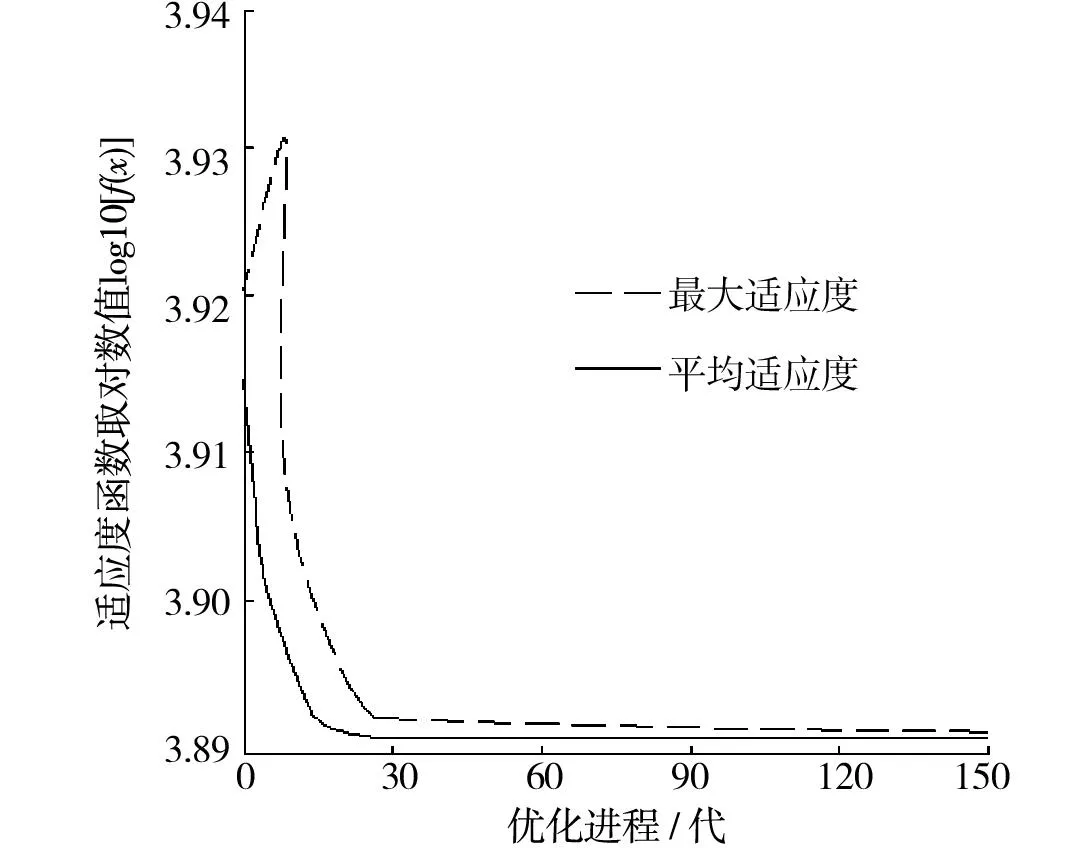
图4　优化过程中目标函数值变化曲线Fig.4 Variation of the fitness value in optimization process

图4显示，遗传单纯元算法融合了GA的全局搜索能力和SA的局部搜索能力，进化速率很快，目标值稳定下降，当优化过程进行到28代之后，最大适应度值和平均适应度值趋于稳定，隐含层最优中心值已获得，采用遗传单纯元算法很大程度地提高了中心值最优的获取速率。并通过GSA—RBF网络隐含层的无导师训练及输出层的有导师训练，建立输入样本-输出样本两者的非线性映射关系。

第4步: GSA—RBF网络模型检验。

将第19组通过FLAC3D模型正分析计算所得的5个测点的地应力值归一化后作为输入样本，代入前面训练好的GSA—RBF网络进行反演，并将反演得到的岩体力学参数及侧压力系数代入FLAC3D模型进行计算，把结果与本步前面正分析计算所得的地应力值进行对比，若结果相符，说明第3步建立的输入样本-输出样本两者的映射关系满足要求；如果不符合，则需重新训练GSA—RBF网络，直至映射关系满足要求。

第5步:实测点地应力值反演。

将5个测点的地应力实测值作为输入向量代入第3步中检验好的GSA—RBF网络，得到相应的岩体力学参数及侧压力系数，再将得到的参数代入FLAC3D模型进行计算，进而得到该5个测点初始地应力的反演结果(见表2)，其与实测值的相对误差在初始地应力值测量的允许误差内，表明本文使用的GSA—RBF网络进行初始地应力反演是合理有效的。

为了突出GSA—RBF网络性能的提升，本文同时采用GA—RBF网络和标准RBF网络进行反演计算，反演过程和GSA—RBF网络反演过程大致相同，在此不再赘述。为了有效地分析，将3种算法的反演结果与实测值比较，见表2。

表2显示，利用GSA—RBF网络进行反演的相对误差最大值为5.38，最小值为0.09；利用GA—RBF网络进行反演的相对误差最大值为11.22，最小值为0.27；利用标准RBF网络进行反演的相对误差最大值为20.58，最小值为0.79。国内外统计的资料表明，初始地应力值测量的允许误差达到25%～30%[18]。虽然3种方法的计算精度都能够较好的满足工程要求，但GSA—RBF网络总体的相对误差最小，精度最高，计算收敛代数少，网络性能得到很大程度的提高。

表2　地应力实测值与反演值的比较

注：表中相对误差1,2和3列数据分别表示GSA—RBF网络、GA—RBF网络、标准RBF网络与实测值之间的相对误差。

5结论

1)本文的GSA—RBF网络与GA-RBF网络与标准RBF网络相比，其突出的优点是利用遗传单纯元算法融合的2种搜索机制搜索最优的径向基函数中心值，不被聚类中心影响，提高了利用RBF网络反演初始地应力的精度，且由算例分析的反演结果证明了该方法的可行性。

2)RBF网络的结构及参数包括隐层节点数、隐层中心值、宽度及隐层至输出层的连接权值，而本文仅优化了隐层中心值，条件允许下，可进一步利用遗传算法或其他方法优化网络其他参数(如利用自适应梯度下降法选择宽度、使用递推的最小二乘法优化权值)来反演初始地应力。

参考文献：

[1] 孙均,蒋树屏,袁勇,等.岩石力学反演问题的随机理论与方法[M].汕头:汕头大学出版社,1996.

SUN Jun, JIANG Shuping, YUAN Yong, et al. Random theory and method of feedback analysis in geotechnical mechanics.[M].Shantou :Shantou University Press,1996.

[2] 杨林德,冯紫良,朱合华,等.岩土工程问题的反演理论与工程实践[M].北京:科学出版社,1996.

YANG Linde, FENG Ziliang, ZHU Hehua, et al. Back analysis theories and applications to geotechnical engineering[M]. Beijing：Science Press,1996.

[3] 王金安,黄琨,张然.高陡复杂露天矿边坡地应力场分区非线性反演分析[J]. 岩土力学,2013,34(增刊2):214-221.

WANG Jinan, HUANG Kun, ZHANG Ran. Sub-regional nonlinear in-situ stress inversion analysis of complex high steep slope of open pit[J]．Rock and Soil Mechanics,2013,34(Suup 2)：214-221．

[4] 裴启涛,李海波,刘亚群.南水北调西线工程坝区初始地应力场反演分析[J].岩土力学,2012,33(增2):338-344.

PEI Qitao, LI Haibo, LIU Yaqun. Back analysis of initial geostress field of dam site in west route of South-to-North water transfer project.[J]．Rock and Soil Mechanics,2012,33(Suup 2)：338-344．

[5] 张延新,宋常胜,蔡美峰,等.深孔水压致裂地应力测量及应力场反演分析[J].岩石力学与工程学报,2010,29(4):779-785.

ZHANG Yanxin, SONG Changsheng, CAI Meifeng,et al. Geostress measurements by hydraulic fracturing method at great depth of boreholes and numerical modeling predictions of stress field[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(4):779-785.

[6] 陈章华,陈磊,纪洪广.基于偏最小二乘法的地应力场拟合[J]. 北京科技大学学报,2013,35(1):1-7.

CHEN Zhanghua,CHEN Lei,JI Hongguang.Geo-stress field fitting based on the Partia l least square method[J]. Journal of University of Science and Technology Beijing,2013,35(1):1-7.

[7] 景锋,盛谦,张勇慧,等．我国原位地应力测量与地应力场分析研究进展[J]．岩土力学,2011,32(增刊2):51-58.

JING Feng, SHENG Qian, ZHANG Yonghui, et al． Study advance on in-site geostress measurement and analysis of initial geostress field in China[J]． Rock and Soil Mechanics,2011,32 (Supp2): 51-58.

[8] 周家文, 杨兴国, 吴震宇,等.浅埋岩体隧洞初始地应力场位移反分析方法研究[J].四川大学学报,2010,9(1): 48-56.

ZHOU Jiawen, YANG Xingguo, WU Zhenyu, et al.Displacement back analysis of initial stresses filed of shallow rock masses tunnel[J]. Journal of Sichuan University, 2010, 9(6): 48-56.

[9] 赵德安,李国良,陈志敏,等．乌鞘岭隧道三维地应力场多元有限元回归拓展分析[J]．岩石力学与工程学报,2009,28 (增刊1):2687-2694．

ZHAO Dean, LI Guoliang, CHEN Zhimin, et al. Three-dimensional FE regression analysis of multivariate geostress field of Wushaoling tunnel[J]. Chinese Journal of Rock Mechanics and Engineering,2009,28(Supp1): 2687-2694．

[10] 夏江, 严平, 庄一舟,等.基于遗传算法的软土地基沉降预测[J].岩土力学, 2004, 25(7): 1131-1134.

XIA Jiang, YAN Ping, ZHUANG Yizhou, et al. Prediction of soft soil foundations settlements based on genetic algorithm[J]. Rock and Soil Mechanics,2004,25(7): 1131-1134.

[11] 张航, 高正夏.遗传退火算法在木兰溪防洪工程软基沉降预测中的应用研究[J].路基工程, 2012(6):99-105.

ZHANG Hang, GAO Zhengxia. Application of genetic annealing algorithm in flood control projects Mulan soft ground settlement prediction[J]. Subgrade Engineering, 2012(6):99-105.

[12] 王树栋．基于进化神经元算法的堡镇隧道软弱围岩施工弹塑性智能位移反分析[J].北京交通大学学报,2010,34(3):112-116．

WANG Shudong． Elasto-plastic intelligence displacement back analysis of Softock construction in Baozhen tunnel based on evolutionary-neuron algorithm[J]. Journal of Beijing Jiaotong University,2010,34(3):112-116．

[13] 张乐文,张德永,邱道宏.径向基函数神经网络在地应力场反演中的应用[J].岩土力学,2012,33(3)：799-804．

ZHANG Lewen, ZHANG Deyong, QIU Daohong.Application of radial basis function neural network to geostress field back analysis[J]．Rock and Soil Mechanics,2012,33(3)：799-804．

[14] JING G L, DU W T, GUO Y Y. Studies on prediction of separation percent in electro dialysis process via BP neural networks and improved BP algorithms[J].Desalination,2012,291(1):78-93.

[15] Nelder J A , Mead R. A simplex method for function minimization [J] . Computer J,1965,7(2):308-313.

[16] 张建文，王煜薇，郑小平，等.基于混合遗传-Nelder Mead单纯形算法的源强及位置反算[J].系统工程理论与实践，2011,31(8):1581-1586.

ZHANG Jianwen, WANG Yuwei, ZHENG Xiaoping,et al.Back-calculation of source strength and position by a hybrid genetic-nelder mead simplex algorithm[J].Systems Engineering-Theory & Practice,2011,31(8):1581-1586.

[17] Tuan L A, Bhattacharya K. Competitive framework for procurement of interruptible load services[C]//IEEE Trans on Power Systems,2003,18(2):8892012,33(3)：799-804．897.

[18] 蒋中明,徐卫亚,邵建富.基于人工神经网络的初始地应力场三维反分析[J].河海大学学报,2002, 30(3): 52-56.

JIANG Zhongming,XU Weiya,SHAO Jianfu. ANN-based 3-D back analysis of initial stress in rock masses[J].Journal of Hohai University,2002,30(3):52-56.

Back analysis of geostress field with RBF

neural network and genetic-simplex algorithm

XIE Xuebin1，LUO Haixia1，YNAG Chengxiang2，LI Xin1

(1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China；

2. Anhui Tongguan (Lujiang) Mining Co., Ltd, Tongling 231561, China)

Abstract:To enhance the performance of RBF neural network, genetic- simplex algorithm(GSA) is used to optimize the central value in the hidden layer of RBF neural network. A numerical model of the area is established by FLAC3Dto conduct positive analysis. taken measured normal stresses of some specific points as the training sample, the optimized RBF neural network (GSA-RBF) was utilized to conduct back analyses for rock mechanical parameters and initial stress field. Based on geological data of Shaxi copper mine, the results obtained from back analysis were compared with those by GSA-RBF and the measured ones, and the comparison results show that the back analysis method of GSA-RBF is feasible, and improves the calculation accuracy, which provides certain reference value to the similar engineering projects.

Key words:initial stress field; back analysis; FLAC3D; genetic algorithm; simplex algorithm; RBF neural network

中图分类号：TU443

文献标志码：A

文章编号：1672-7029(2015)01-0072-07

通讯作者：谢学斌(1968-)，男，湖南祁东人，教授，博士，从事岩土工程的科研和教学工作;E-mail:xbxie@csu.edu.cn

基金项目：安徽省科技攻关计划资助项目(12010402148)

*收稿日期：2014-06-06