基于粒子群BP网络混合算法的边坡稳定性评价



基于粒子群BP网络混合算法的边坡稳定性评价

胡卫东1，2，曹文贵1

(1. 湖南大学 岩土工程研究所，湖南 长沙 410082；

2. 湖南理工学院 土木建筑工程学院，湖南 岳阳 414000)

摘要:边坡稳定性评价与预测具有高度非线性和不确定性特征，难以用准确的数学模型表达。选取多个边坡工程实例构成学习样本集，以土体重度、内摩擦角、黏聚力、坡角、坡高、孔隙压力比6个主要影响因素作为土坡稳定性的评价判别指标；然后采用粒子群算法优化BP神经网络模型，实现混合算法，在保持BP网络算法误差反向传播修正权值特点的同时，将网络权值和阈值粒子化，利用粒子群算法的全局搜索性实现网络权值和阈值的更新，从而加快收敛速度和提高收敛精度，避免传统粒子群结合BP网络算法的“早熟”现象；通过与其他算法进行边坡稳定性评价的比较分析，表明了本文研究算法的可行性与合理性。

关键词：边坡稳定性；粒子群算法；BP神经网络；混合算法；优化

边坡稳定性分析与评价是边坡工程的核心内容，由于对边坡破坏机理的研究不够完善，影响边坡工程稳定性的因素存在随机性、模糊性和可变性及岩土参数选择的主观性[1]，边坡稳定性评价存在很大程度的不确定性，给边坡稳定性评价与预测带来了困难，因此，建立一种能考虑众多非线性因素共同作用的边坡稳定性评价与预测方法成为本文的出发点。目前，边坡稳定性评价与预测方法主要有回归分析模型、模糊数学方法、灰色预测方法和人工神经网络模型等[2]。现有研究人工神经网络方法中普遍采用的BP神经网络模型，由于能够充分考虑众多非线性因素对边坡稳定性的影响,实现对任意函数的逼近，已经得到了较为广泛的应用,但是，BP神经网络模型基于梯度下降算法由于存在易陷入局部极小、算法收敛速度慢和泛化能力弱等难以避免的问题[3]，在运用到实际工程当中仍然需要加以改进，于是，出现了采用遗传算法、蚁群算法和粒子群算法等算法与BP神经网络相结合的方法[4]，以弥补神经网络模型的不足，改善神经网络模型的结构，加速算法的收敛，提高预测分析的精度。

根据现有传统的基于粒子群算法优化BP神经网络模型的研究方法，将网络的权值和阈值粒子化，利用粒子位置的更新实现网络权值和阈值的更新，能够加快网络训练收敛速度，提高误差精度[5-6]，但粒子群中的粒子经常会出现“早熟”收敛现象，粒子群出现趋同性而使得算法陷入局部极小值，并且忽略了BP网络模型的误差反向传播修正权值算法的优点。基于以上问题，本文考虑采用粒子群与BP神经网络的混合算法，粒子利用适应度值进行网络最优权值的搜索过程中，对粒子群的个体最优值和全局最优值按照BP网络误差反向传播算法不断进行更新，在保持BP网络算法反向传播特点的同时来实现粒子群算法的全局搜索，抑制粒子“早熟”的产生。

1BP神经网络算法

BP(Back Propagation)网络[1]是一种按误差反向传播算法训练的多层前馈型神经网络，是最为广泛的人工神经网络之一，典型BP网络包含输入层、输出层和至少1个隐含层。学习过程分为正向传播和逆向传播2个阶段，第1个阶段正向传播，输入信号从输入层到隐含层再到输出层逐层处理，每个神经元均由输入、激活函数和阈值来决定活化程度；第2个阶段，计算输出误差，并进行反方向传播，不断修正各层神经元间的权值和阈值，使得误差的目标函数最小。

BP网络前向传播输出节点的传递函数通常采用Sigmoid函数

(1)

BP神经网络算法应用梯度下降法加快收敛速度，调整和修正权值使得误差最小，其权值调整公式为

(2)

(3)

式中：η为学习率；Ek为BP网络算法批处理方式下所有样本第k次输入后的整体均方差，即目标优化函数，其具体表达式为：

(4)

式中：m为训练样本集的样本个数；q为网络输出神经元个数；Yij为第i个样本第j个期望输出值，tij为第i个样本第j个实际输出值。

BP网络算法能够实现从输入空间到输出空间的非线性映射，是一个非线性优化问题，仍不可避免地存在局部极小值问题，容易陷入局部极值且收敛速度较慢。本文针对上述问题，将粒子群算法和BP网络算法相结合，用粒子群算法代替BP网络算法中的梯度下降法，改善BP网络算法性能。

2粒子群优化算法

粒子群优化算法是由Kennedy和Eberhart最早提出的群体智能优化算法[7-8]，该方法模拟鸟群觅食过程，通过群体迭代，在群体粒子中寻找目标解空间中的最优粒子。在粒子群算法中，每个优化问题的解都是一个粒子，被看成是一只空间飞行的鸟，在解空间中搜索个体最优解和全局最优解。

粒子群算法首先初始化一群随机粒子，粒子向量的维数n由实际优化问题决定，每个粒子的位置向量表示n维搜索空间中的一点，也就是n维优化空间的一个解。Xj表示第j个粒子当前位置向量：

Xj=Xj1,Xj2,…Xjn

(5)

Vj表示第j个粒子的当前速度向量:

Vj=Vj1,Vj2,…Vjn

(6)

在每次迭代过程中，首先将粒子位置向量代入粒子群算法的适应度函数，即目标优化函数Ek，求出的目标函数值也就是粒子的适应度值，然后通过比较最优适应度值搜索粒子群历代自身的最佳位置Pj和全局最佳位置Gj，即

Pj=Pj1,Pj2,…Pjn

(7)

Gj=Gj1,Gj2,…Gjn

(8)

式中：Pj为历代搜索过程中每个粒子自身所达到的个体最优解，Gj为历代搜索过程中所有粒子所达到的全局最优解，也就是粒子群算法的最优解，粒子群根据这两个值Pj与Gj及当前位置Xj与速度Vj来进行粒子的更新优化，得到迭代后的位置与速度向量，粒子群算法的进化方程可描述为：

Vj(k+1)=w·Vj(k)+c1·r1·(Pj(k)-

Xj(k))+c2·r2·(Gj(k)-Xj(k))

(9)

Xj(k+1)=Xj(k)+Vj(k+1)

(10)

式中：w表示惯性权重；c1和c2表示学习因子，一般在0-2之间取值，通常取2；r1和r2是介于[0,1]间的两个独立随机数，一般采用均匀分布；k和k+1分别表示第k代与第k+1代；j表示第j个粒子。粒子在更新优化过程中还应受到最大速度vmax的限制以避免盲目搜索，通常Vi在[-vmax,vmax]范围内。

惯性权重w对粒子群优化算法的性能影响较大，w较大时，有利于全局优化搜索，w变小具有较强局部搜索优化能力，根据已有研究采用自适应调整惯性权重，随着算法迭代次数增加而线性减小，其表达式为

(11)

其中，k为当前迭代步数;kmax为最大迭代步数;wmax和wmin分别为w的最大值与最小值，一般取为wmax=0.9，wmin=0.4。

传统基于粒子群优化算法的BP神经网络在训练参数过程中，将网络权值和阈值粒子化，每个粒子能够唯一确定网络的权值和阈值，对粒子群中粒子的位置向量不断更新优化就是对神经网络的权值和阈值进行不断地更新，从而达到优化网络的目的。

3粒子群与BP神经网络混合算法

已有研究表明，传统的粒子群算法与BP网络算法相结合方法直接利用粒子群算法对BP网络的权值和阈值进行更新优化，会使得粒子出现“早熟”收敛现象，粒子群中的粒子出现“聚集”，表现出强烈趋同性而陷入局部极小值[9-10]。为此，本文对传统的粒子群BP网络算法进行改进，引入2种算法的混合算法，以解决优化算法中“早熟”收敛问题，实现全局优化。

为了避免“早熟”，通过在优化过程中不断调整粒子最佳位置和群体最佳位置使得粒子从“聚集”到“飞散”，可使得传统粒子群算法跳出局部最优，从而提高粒子群求得全局最优解的能力，并改善神经网络的收敛精度。算法具体步骤如下：

(1)初始化BP神经网络，确定网络结构，设定输入层、隐含层、输出层的神经元个数。

(2)确定粒子群规模M、维数n，初始化粒子群中每个粒子的位置向量Xj和速度向量Vj。粒子群的规模即粒子的个数，一般在几十至上百个，视具体情况而定，粒子维数的具体表达式为

n=n1+n2+n3+n4

(12)

式中：n1表示输入层与隐含层间的连接权值个数；n2表示隐含层与输出层间的连接权值个数；n3表示隐含层的阈值个数；n4表示输出层的阈值个数。

(3)计算粒子适应度值。按批处理方式，对每个粒子输入所有样本的数据，进行网络的前向传播计算，产生训练误差，然后依据公式(4)逐个计算粒子的样本集均方差Ek，即粒子的适应度值。

(4)比较适应度值，确定每个粒子的个体最优解和所有粒子的全局最优解。在迭代过程中，如粒子的当前适应度值小于粒子历代个体最优解的适应度值，则取粒子的最优解Pj为当前的粒子位置向量，否则不变；在当前一轮迭代过程中，如有粒子的当前适应度值小于粒子群历代全局最优解的适应度值，则取粒子群的最优解Gj为当前的粒子位置向量，否则不变。

(5)根据BP网络算法公式(2)和(3)，对每个粒子的最优解向量Pj和粒子群的全局最优解向量Gj进行更新。

(6)更新粒子群每个粒子的位置和速度向量。首先，确定最大迭代次数kmax,惯性权重w,学习因子c1和c2；然后，根据粒子群算法公式(9)和(10)更新粒子的速度和位置向量，并要求更新后的速度和位置限定在相应范围内。

(7)结束条件的判断。比较迭代次数是否达到设定最大迭代次数，如果满足则迭代结束；或者目标优化函数式(4)即整体均方差是否达到设定精度要求，若算法收敛，满足精度要求则退出迭代过程，此时，最后一次迭代的全局最优解也就是问题的解，全局最优解向量中的每一维也就是网络结构的权值与阈值。如果不满足上述迭代次数和精度要求，则算法继续迭代，返回第(3)步骤。

粒子群BP神经网络混合学习算法的具体实现流程如图1所示，上述算法能够实现粒子群算法与BP网络算法的充分融合，既充分体现了BP网络算法误差反向传播特点，又很好利用了粒子群算法全局搜索的能力。

图1　粒子群BP网络混合算法流程图Fig.1 The BP neural network with particle swarmhybrid algorithm process

4边坡稳定性评价模型

4.1样本训练参数选取

以文献[11]中的20个土质边坡工程为例[11]，如表1所示，以土体重度γ,内摩擦角φ,黏聚力c,坡角η,坡高H和孔隙压力比μ等6个主要影响因素作为评价指标和网络输入[12-13]；以边坡的稳定系数作为网络输出。将总体样本分为2组，样本库的前15个样本作为学习样本组，用来训练网络；样本库的后5个样本作为检验样本组，用以检验建立的网络模型准确性。

4.2网络结构及算法参数确定

本文BP网络采用3层结构模型，包括6个输入节点，1个输出节点，13个中间隐含层节点,于是确定网络结构为6-13-1,神经网络训练时采用Sigmoid函数为传递函数。同时，为了消除各判别因素的量纲和数量级不同所带来的影响，防止某些数值低的特征被淹没，需要在训练前统一对训练样本进行归一化处理，使其成为相同数量级，其具体计算表达式为

(13)

式中：xmax和xmin分别为每组样本的最大值和最小值；x和x'分别表示原始样本归一化处理前后的数据；考虑到Sigmoid函数在[0,0.1]与[0.9,1.0]区域内曲线变化非常平坦，于是将经过归一化之后样本数据取值范围限制在[0.1，0.9]之间。

为了提高学习速度和增加BP网络算法的可靠性，采用有动量项的梯度下降法，可以有效减小学习过程的振荡趋势，从而改善算法收敛性。

规定粒子群规模为M=20，粒子的维数n=105，最大迭代次数为kmax=200，惯性权重w随迭代次数增加而线性减小，范围为[wmin,wmax]=[0.4,0.9]，学习因子c1=c2=2，粒子飞行最大速度为vmax=0.5。

4.3网络优化训练

采用粒子群优化BP神经网络混合算法，在Matlab环境中编程，并将土坡稳定工程的学习样本数据代入对网络进行训练。算法在迭代次数达到340步时，粒子群全局最优解与粒子个体最优解趋于稳定，适应度值满足要求(Ek<0.001)，网络达到设定的误差精度，优化过程结束。优化算法的粒子群全局适应度值随迭代次数的变化过程如图2所示，从图中可以看出，算法收敛很快，经过较少迭代次数就可满足精度要求。

表1　学习样本的实际输出与期望输出

4.4网络训练结果对比分析

利用训练好的混合算法网络模型对预测样本进行预测，并与采用BP神经网络模型预测的结果进行比较，如表2所示，可以看出本文研究方法的误差较小，达到预期的目标，通过误差对比表明通过基于粒子群算法优化BP网络模型所建立的非线性映射关系是准确的，其相对误差更小，训练效果更好，网络具有较好的泛化性能。

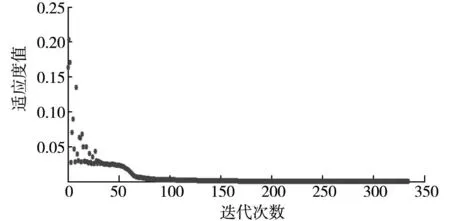
图2　粒子群适应度值变化曲线Fig.2 Fitness curve of particle swarm

样本编号重度γ/KN·(m3)-1黏聚力c/KPa内摩擦角φ/(°)坡角η/(°)坡高H/m孔隙压力比μ理想输出FLBP网络输出混合算法输出1625.0046.0035.0046.00393.000.251.311.3871.3671725.0048.0040.0049.00330.000.251.491.4661.5011831.3068.6037.0047.00305.000.251.201.2041.2011925.0055.0036.0045.50299.000.251.521.4981.5222031.3068.0037.0047.00213.000.251.201.1291.199

5结论

1)采用利用粒子群算法优化BP神经网络计算不需要事先建立任何理论模型，避开了不知道滑移面和岩体破坏机制等不确定因素，具有自动学习、收敛速度快、容错能力较强和高度的非线性等特征，克服了传统方法非线性数学建模的困难。

2)提出基于粒子群与BP神经网络混合优化算法对边坡稳定性评价与预测，将网络权值和阈值粒子化，以样本的误差均方差为粒子的适应度值，利用粒子群优化方法和BP网络算法进行网络最优权值的混合搜索，能够保持BP网络算法固有的误差反向传播修正权值特点的同时，避免传统的粒子群BP网络算法容易陷入局部极值等现象，提高求解全局最优解的能力，从而改善神经网络的性能。

3)通过与其他边坡稳定性评价算法进行比较分析，表明了本文研究算法的可行性与合理性。

参考文献：

[1] 冯夏庭,王泳嘉，卢世宗，等.边坡稳定性的神经网络估计[J].工程地质学报,1995,3(4):54-61.

FENG Xiating, WANG Yongjia, LU Shizong, et al.Neural network estimation of slope stability[J].Journal of Engineering Geology,1995, 3(4):54-61.

[2] 胡卫东,陈积光.边坡稳定分析的神经网络方法[J].建筑技术开发, 2011,38(1): 7-10.

HU Weidong,CHEN Jiguang.Slope stability analysis with artifical neural network method[J].Building Technique Development, 2011,38(1): 7-10.

[3] 徐以山,曾 碧,尹秀文,等.基于改进粒子群算法的 BP 神经网络及其应用[J].计算机工程与应用,2009, 45 (35):233-235.

XU Yishan,ZENG Bi,YIN Xiuwen,et al.BP neural network and its applications based on improved PSO[J].Computer Engineering and Applications,2009,45(35):233-235.

[4] 江丽,王爱平.基于粒子群与 BP 混合算法的神经网络学习方法[J].计算机应用, 2012,32( S2) :13-15.

JIANG Li,WANG Aiping.Hybrid neural network algorithm method based on particle swarm optimization and BP neural network algorithm[J].Journal of Computer Applications, 2012,32( S2) :13-15.

[5] McCombie P,Wilkinson P.The use of the simple genetic algorithm in finding the critical factor of safety in slope stability analysis[J].Computers and Geotechnics,2002,29(8):699-714.

[6] 朱珍德,杨喜庆,郝振群,等.基于粒子群优化BP神经网络的隧道围岩位移反演分析[J].水利与建筑工程学报, 2010,8(4):16-20.

ZHU Zhende,YANG Xiqing,HAO Zhenqun,et al. Research on displacement back-analysis of tunnel surrounding rock based on BP neural network optimized by particle swarm[J].Journal of Water Resources and Architectural Engineering, 2010,8(4):16-20.

[7] Kannana S,Mary S,Slochanal R,et al.Application of particle swarm optimization technique and its variants to generation expansion planning problem[J].Electric Power Systems Research,2004,70(8):203-210.

[8] Kennedy J, Eberhart R C. Particle swarm optimization [C]//Proc IEEE int Conf on Networks Vol. IEEE Service Center,Piscataway,NJ,1995:1942-1948.

[9] 刘坤,谭营,何新贵.基于粒子群优化的过程神经网络学习算法[J].北京大学学报(自然科学版),2011,47(2):238 -244．

LIU Kun,TAN Yin,HE Xingui.Particle swarm optimization based learning algorithm for process neural networks[J].Acta Scientiarum Naturalium Universitatis Pekinensis,2011,47(2):238 -244．

[10] 江龙艳.基于PSO-BP神经网络的边坡稳定性模型研究[J].有色金属, 2013,65(6): 53-57.

JIANG Longyan.Study on slope stability model by PSO-BP neural network[J].Nonferrous Metals(Mining Section), 2013,65(6): 53-57.

[11] 何锋,吴树仁,张怡权,等. 圆弧形公路边坡稳定性分析的神经网络法[J].地球学报, 2004,25(1): 95-98.

HE Feng,WU Shuren,ZHANG Yiquan,et al.A neural network method for analyzing compass slope stability[J]. Acta Geoscientica Sinica, 2004,25(1): 95-98.

[12] 汤祖平,李亮,赵炼恒,等.含软弱夹层边坡稳定性的极限分析上限解析[J].铁道科学与工程学报, 2014,11(2): 60-64.

TANG Zuping,LI Liang,ZHAO Lianhen,et al.Stability analysis of slopes with weak interlayer based on upper bound limit analysis[J].Journal of Railway Science and Engineering, 2014,11(2): 60-64.

[13] 王路路,潘秋景,杨小礼.三级台阶边坡稳定性分析的上限解研究[J].铁道科学与工程学报, 2013,10(3): 43-46.

WANG Lulu,PAN Qiujing,YANG Xiaoli.Upper bound solution for stability analysis of tri-beaches slope[J]. Journal of Railway Science and Engineering, 2013,10(3): 43-46.

Slope stability evaluation based on hybrid algorithm of

particle swarm optimization and BP neural network

HU Weidong1, 2，CAO Wengui1

(1. Institute of Geotechnical Engineering, Hunan University, Changsha 410082, China;

2. School of Civil and Architectural Engineering, Hunan Institute of Science and Technology, Yueyang 414000, China)

Abstract:It is highly nonlinear and uncertain to evaluate and predict slope stability, and also difficult to express using accurate mathematical model. Firstly, the multiple slope engineering instances were adopted to constitute a learning sample set. The six main influence factors, including soil density, internal friction angle, cohesion, slope angle, slope height, void ratio, composed slope stability evaluation index. Then BP neural network model was optimized using particle swarm optimization algorithm to realize the hybrid algorithm. When maintaining the BP network algorithm of error back propagation correction weight, the network weights and threshold values were particles and updated using particle swarm algorithm global searching. At the same time the convergence speed was accelerated and the convergence precision was improved. The “premature” phenomenon for the BP network algorithm combining with traditional particle swarm was avoided. Finally, the feasibility and rationality of the proposed approach in the paper were verified in comparison with other slope stability evaluation algorithms.

Key words:slope stability; particle swarm algorithm; BP neural network; hybrid algorithm; optimization

中图分类号：TP183

文献标志码：A

文章编号：1672-7029(2015)01-0066-06

通讯作者：胡卫东(1976-)，男，湖南岳阳人，副教授，博士研究生，从事边坡稳定与边坡地基承载力研究；E-mail: huweidong506@163.com

基金项目：国家自然科学基金资助项目(51378198)；高等学校博士学科点专项科研基金资助项目(20130161110017)；湖南省教育厅资助项目(11C0618)

*收稿日期：2014-07-09