高速铁路复线隧道内压力波特性的数值模拟研究



高速铁路复线隧道内压力波特性的数值模拟研究

刘希贤，郭安宁，梅元贵，许建林，李士安，周朝晖

(兰州交通大学 机电工程学院，甘肃 兰州 730070)

摘要:采用有限体积方法和任意滑移界面动网格技术的CFD方法，对我国高速列车和复线隧道条件下的压力波基本特性进行数值模拟研究。为避免数值计算产生不合理的物理现象，应用光滑启动技术。在验证本文数值方法正确性的基础上，采用三维非定常可压缩湍流流动模型方法，研究高速列车驶入单洞复线隧道时的压力波基本特征，揭示隧道内压力波的形成过程，得到不同断面上不同测点的压力变化及分布规律；研究结果表明：在初始压缩波三维效应的影响下，近隧道入口断面不同测点压力差异较大，且随着列车速度的增加，正压最大值也越大；在距离出口较近的断面上，当列车速度增加到一定范围，正压最大值反而减小；隧道衬砌上的正压最大值多出现在距离隧道入口较近处，而负压最大值则出现在隧道的中央断面上。

关键词：高速列车；复线隧道；压力波；数值模拟

隧道压力波是高速铁路隧道空气动力学中的一个重要现象，会产生乘客舒适性、列车车体及部件和隧道内固定设备等疲劳强度设计问题[1-4]。随着我国高速铁路的发展，国内开展了实车和动模型试验，揭示了压力波的形成和变化特性[5-10]。隧道压力波的数值模拟方法有一维流动模型和三维流动模型方法。一维流动模型方法能合理地提供隧道断面上的平均压力波特性，并取得了试验验证[1-2,11]。三维流动模型能给出较详细的洞内压力和流速特性，为洞口和列车外形设计等提供依据[5,10,12-14]，并用于列车运行、洞内辅助结构等方面的空气动力特性分析[15-17]。同时，还出现了一维和三维流动模型耦合方法，用于分析长大隧道及隧道群的空气动力效应[18]。高速铁路隧道大多采用单洞复线的形式。列车和隧道形成的几何空间为非对称空间，引起的流动也是非对称的，作用于不同隧道衬砌表面的压力特性也不同，这就提出了合理确定其气动载荷的问题。对于此类问题，目前公开的研究文献尚没有见到报道。因此，本文基于我国高速列车CRH380A，采用基于CFD软件的三维非定常可压缩湍流流动模型，在与发展成熟可靠的一维可压缩非定常模型的特征线求解结果比较基础上，进行隧道压力波的形成机理、隧道断面上压力分布特性等方面的研究，期望为今后的研究提供一定的基础。

1问题描述和数值计算方法

1.1几何模型和计算区域

本文将单洞复线隧道简化为光滑半圆管模型，忽略隧道内的建构造物，同时不考虑隧道外的地形环境，隧道的横断面直径D=13.3 m，横截面面积FTU=100 m2，长LTU=58.6D，线间距0.38D；列车模型采用光滑表面的CRH380A高速列车简化气动模型，忽略转向架和受电弓等部件，轨面以上车高ht=0.28D，长LTR=7.74D；车/隧模型的阻塞比为0.108。本文采用1∶10的缩尺模型。计算区域由隧道空间及其端口外的开阔空间构成，两者横截面为同心圆弧，开阔空间半径15D。以隧道入口平面内隧道中心线与轨面的交点为坐标原点，列车前进方向为x正方向，铅垂向上为z正方向，按右手准则建立直角坐标系。图1为计算区域和简化的列车模型。图2为隧道内含测点的断面位置和测点布置示意图。在结果分析中，定义高速列车到达隧道入口端的时刻为t=0。

1.2流动模型及定解条件

高速列车通过隧道引起的空气流动是三维非定常可压缩湍流流动。流动控制方程有连续性方程、动量方程和能量方程。本文采用的湍流模型和壁面处理模型分别为SST k-ω高雷诺数湍流模型和非平衡壁面函数法[19]。高速列车通过隧道时的边界区域如图3所示，其中隧道表面和地面为无滑移静止壁面，伸入计算区域流体的隧道部分为无滑移挡板边界，两侧均为无滑移静止壁面，高速列车表面为无滑移运动壁面。这些固体壁面均为绝热边界。隧道外开阔空间的各表面为常温常压的黎曼边界。为避免列车模型突然启动产生的不合理物理现象，应用了光滑启动技术。在求解初始时刻，高速列车处于静止状态，其周围流场也静止，按海平面国际标准大气条件确定参考压力和温度状态，湍流物理量处处为0。

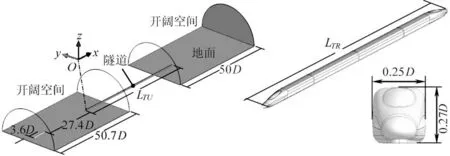
图1　计算区域和高速列车几何模型Fig.1 Sketch of computational domain and train model

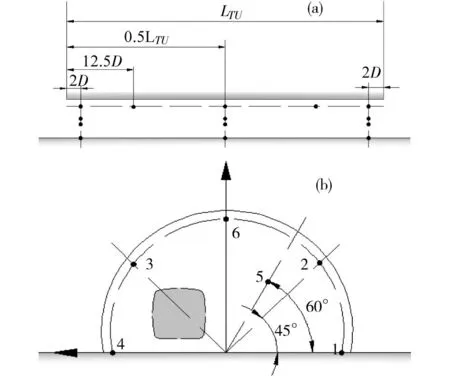
(a)纵断面测点位置;(b)横断面测点位置图2　隧道内典型断面测点位置示意图Fig.2 Sketch of pressure monitors in tunnel

1.3网格划分策略

应用STAR-CD软件的ASI技术求解高速列车通过隧道的问题，将整个计算区域分为静止和运动两大部分，两者之间的交界面构成滑移界面，动静网格通过“耦合—求解—解耦—运动—再耦合，实现滑移网格的计算。在网格划分中，将动、静2部分作为2个单独的“体(Body)”处理，同时将列车周围区域的网格从运动网格中单独分出来作为一个“体(Body)”，以进行适度加密。这样形成3个体的多块网格划分方法，其中列车周围区域完全包含于运动部分之中，两者之间的交界面用网格耦合处理。网格划分采用软件ICEM-CFD，网格总数约为420万。其中，高速列车表面法向第1层网格的厚度按照y+=50取定，流向的网格尺度为Dx+=9～152y+，展向的网格尺度为Dz+=5～52y+。计算区域体网格的尺度依照光顺过渡原则向四周延伸，拉伸比为1.2～2。图4为列车在隧道内运行的面网格划分结果示意图。

图3　网格分布规划与多体网格划分策略Fig.3 Layout of grid distribution and the strategy of multi-body grid generation

图4　列车和隧道表面网格示意图Fig.4 Surface mesh of the train and the tunnel

1.4数值计算方法

采用压力修正算法中的PISO算法求解列车通过隧道引起的流动控制方程。各方程时间项的离散格式为欧拉隐格式，扩散项的离散格式采用中心差分格式，对流项的离散格式采用MARS格式。代数方程组的求解方法为代数多重网格法(AMG)。

在非定常问题的求解中，尽管隐式时间离散格式是无条件稳定的，但实际计算中为减小误差累积，应满足稳定性条件，即

式中:Co为Courant数;|U|=ucell+a，ucell为某点速度,a为当地声速；l为网格特征尺度。用列车表面最小网格尺度和固体壁面法向第1层网格厚度估算时间步长Dt，其典型值为0.018LTR/Vtr。

2计算结果和讨论

2.1数值方法验证

这里采用已发展成熟可靠的一维可压缩非定常不等熵广义黎曼变量特征线方法的计算结果[12]，验证本文三维流动模型方法的正确性和合理性。隧道和列车模型与图1保持一致，一维流动模型计算参数采用原型尺度。列车长度为114 m，速度为350 km/ h，隧道长度为1 140 m。

(a)距隧道入口570 m处的测点压力时间历程曲线;(b)头车车身测点的压力时间历程曲线图5　列车过隧道产生的压力波Fig.5 Pressure wave generated by train passing through the tunnel

图5为本文三维流动模型与一维流动模型计算结果的对比。由图5可见，2种流动模型的计算结果吻合较好，说明本文基于软件的三维流动模型和数值模拟方法能够较好地模拟隧道压力波问题。

2.2压力波的形成

根据图2选取的测点断面获取压力波数据，研究列车过复线隧道的压力波特性。图6～图8分别为距隧道入口2D断面、距隧道入口12.5D断面和距出口2D断面的中央顶部测点“6”的压力和相应断面上平均压力的时间历程曲线。其中，对于图7，t=0.157 2 s为列车车头鼻尖到达x=12.5D断面时刻。由图可见：这3个断面的平均压力和测点“6”的时间历程曲线基本重合，单点测得的压力和断面上平均压力基本相同。同时，从图7得出：当压缩波达到该断面时，测点上压力及断面平均压力均升高，膨胀波经过时，测点压力及断面平均压力均降低。

图6　隧道内距离入口2D处测点及断面平均压力的比较Fig.6 Comparison of presssure change at section 2D from the entry portal and their average pressure

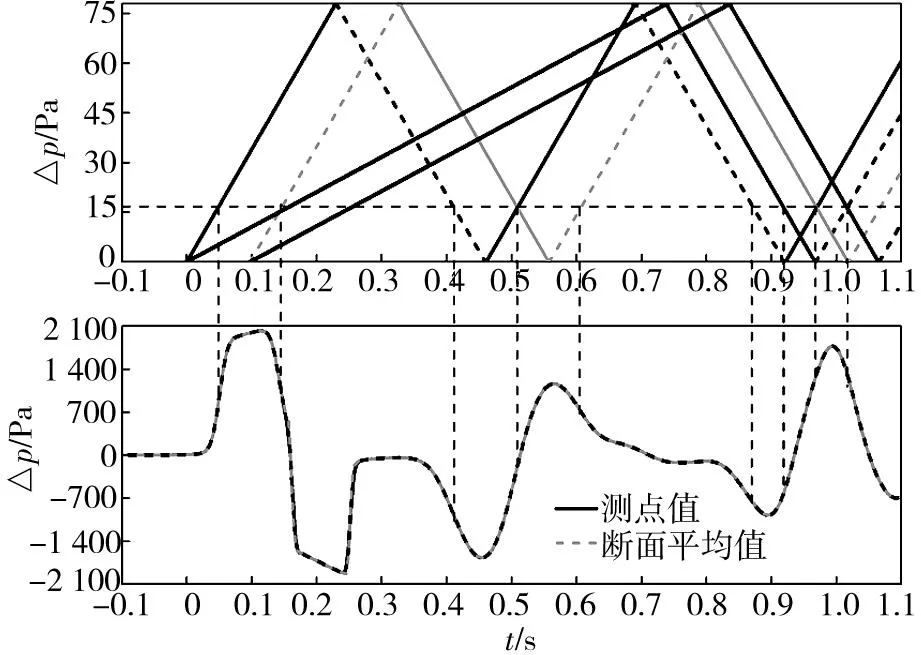
图7　隧道内距离入口12.5D处测点及断面平均压力的比较Fig.7 Comparison of presssure change at section 12.5D from the entry portal and their average pressure

图9为列车通过隧道全过程的压力云图。从图中可以清晰看出：压缩波和膨胀波的产生及传播过程，以及在隧道端口的反射，波系强度的衰减变化的特性。

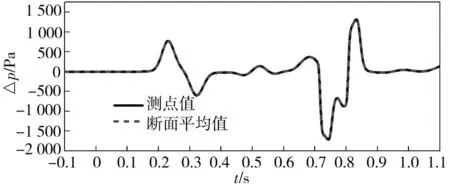
图8　隧道内距离出口2D处测点及断面平均压力的比较Fig.8 Comparison of presssure change at section 2D from the exit portal and their average pressure

图9　列车通过隧道全过程的压力云图Fig.9 Pressure contour of the whole process the train passing through tunnel

2.3不同断面上测点压力差异的比较

图10为隧道内3个不同断面上不同测点的压力时间历程曲线。表1～表3分别统计了3个断面上的压力峰值，表中以远离运行列车的隧道地面测点“1”的压力峰值为基准，得出其他测点与其差值的百分比。其中，列车车头在t=0.025 2 s到达距入口x=2D断面，t=0.369 s到达中央断面，t=0.712 8 s到达距隧道出口x=2D断面。由图表可见：当列车车头、车尾经过测点断面时，断面上不同位置测点的压力不同。

特别是距入口x=2D断面，由于其距隧道入口较近，当t=0.025 2 s，列车头部鼻尖通过时，断面上测点的压力仅受到列车进入隧道产生的初始压缩波影响，在此处这一期间压缩波具有三维效应，导致不同测点压力差异较大；当t=0.034 9 s，列车头部肩部通过;t=0.113 s，列车尾部肩部过;t=0.122 7 s，列车尾部鼻尖通过，由于端部曲线几何变化，也导致了不同测点的压力差异。而在其他时刻，不同测点的压力值几乎一样，并且同一断面不同测点的压力变化趋势基本一致。

(a)距离隧道入口2D断面上不同测点的压力时间历程曲线;(b)隧道中央断面上不同测点的压力时间历程曲线;(c)距离隧道出口2D断面上不同测点的压力时间历程曲线图10　隧道内不同断面上测点的压力时间历程曲线Fig.10 Pressure history on different cross-sections of the tunnel measuring points

对于其他2个断面上不同测点的压力差异，也主要体现在列车头部鼻尖与肩部、列车尾部肩部与鼻尖通过时带来的差异。列车端部通过测点断面带来的压力差异主要原因是：列车和复线隧道形成的几何空间为非对称空间，导致列车与隧道之间的空气流动不对称，加之列车端部曲线几何形状的变化导致流动更为复杂；由于测点“3”和“4”位于靠近车体的隧道一侧，所以这2个测点的正压最大值和负压最大值均要大于其他位置的测点，测点“4”更是受到地面、隧道壁面和列车效应的多重影响，所以使得其正压最大值和负压最大值均要大于其他测点。

2.4隧道内压力分布特征

由图10及表1～表3中还可看出：对于距入口端较近的断面上，不同测点的压力峰值差异较大，三维效应明显。而对于距隧道入口较远的断面和距出口较近的断面，各断面不同测点的压力峰值基本相同。图11和图12分别为列车车头、车尾通过距隧道入口2D断面和中央断面处列车表面和隧道表面的压力分布特征。由图可见：列车车头通过距隧道入口2D的断面时，隧道壁面的压力差异较大，靠近车体一侧的压力明显高于远离车体一侧的压力，三维效应明显，车尾通过隧道入口2D的断面时，隧道壁面的压力差异较小，而列车通过隧道中央断面时，中央断面处的隧道壁面压力相差也较小。

表1隧道入口2D断面上不同测点的压力对比

Table 1 Comparison of the pressure change at different monitors 2D from the entry portal

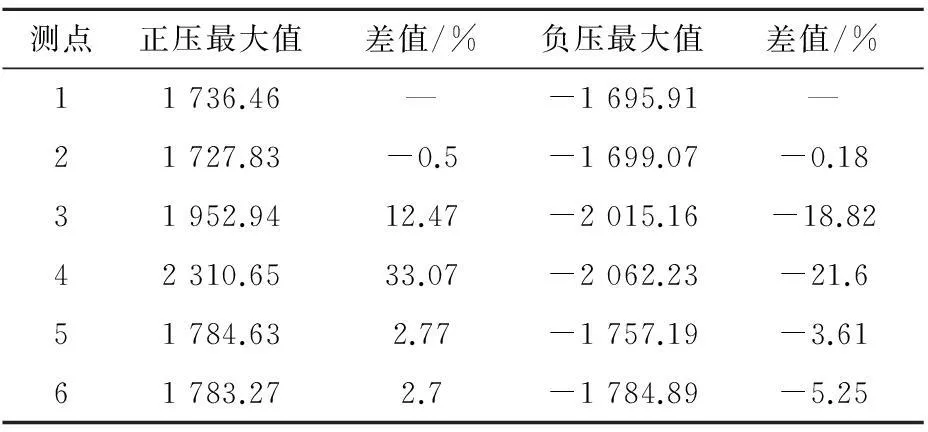
Pa

表2中央断面上不同测点的压力对比

Table 2 Comparison of the pressure change at different monitors at the central cross-section of tunnel

Pa

表3隧道出口2D断面上不同测点的压力对比

Table 3 Compression of the pressure change at different monitors 2D from the exit portal

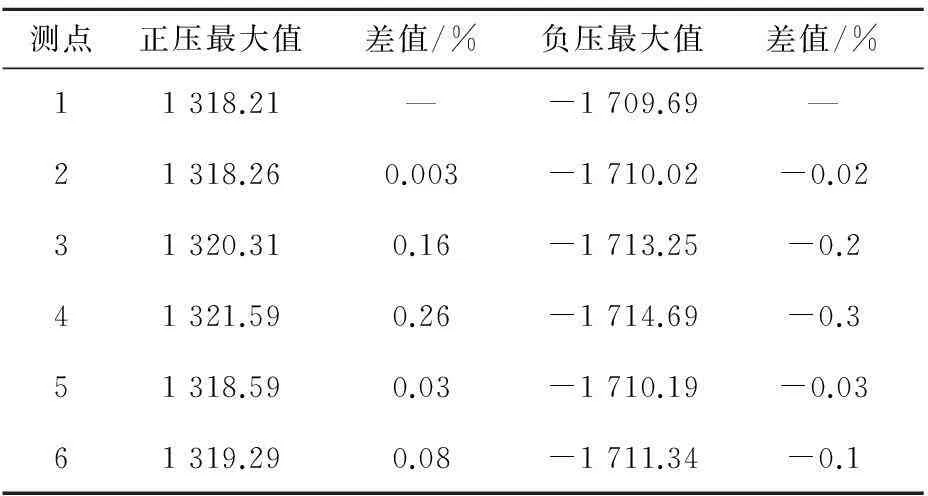
Pa

(a)车头通过;(b)车尾通过图11　隧道入口附近的压力分布Fig.11 Pressure distribution near to the tunnel entrance

(a)车头通过;(b)车尾通过图12　隧道中央处的压力分布Fig.12 Pressure distribution near to the central cross-section of tunnel

2.5列车速度的影响特性

图13为列车速度对距隧道入口2D断面上不同测点正压最大值和负压最大值的影响特性。由图可见：随着车速的增加，各个测点的正压最大值和负压最大值也越来越大。在不同列车速度时，由于上述所分析的原因，距隧道入口2D断面处的正压最大值和负压最大值均出现在近车体隧道一侧的近地测点“4”上。

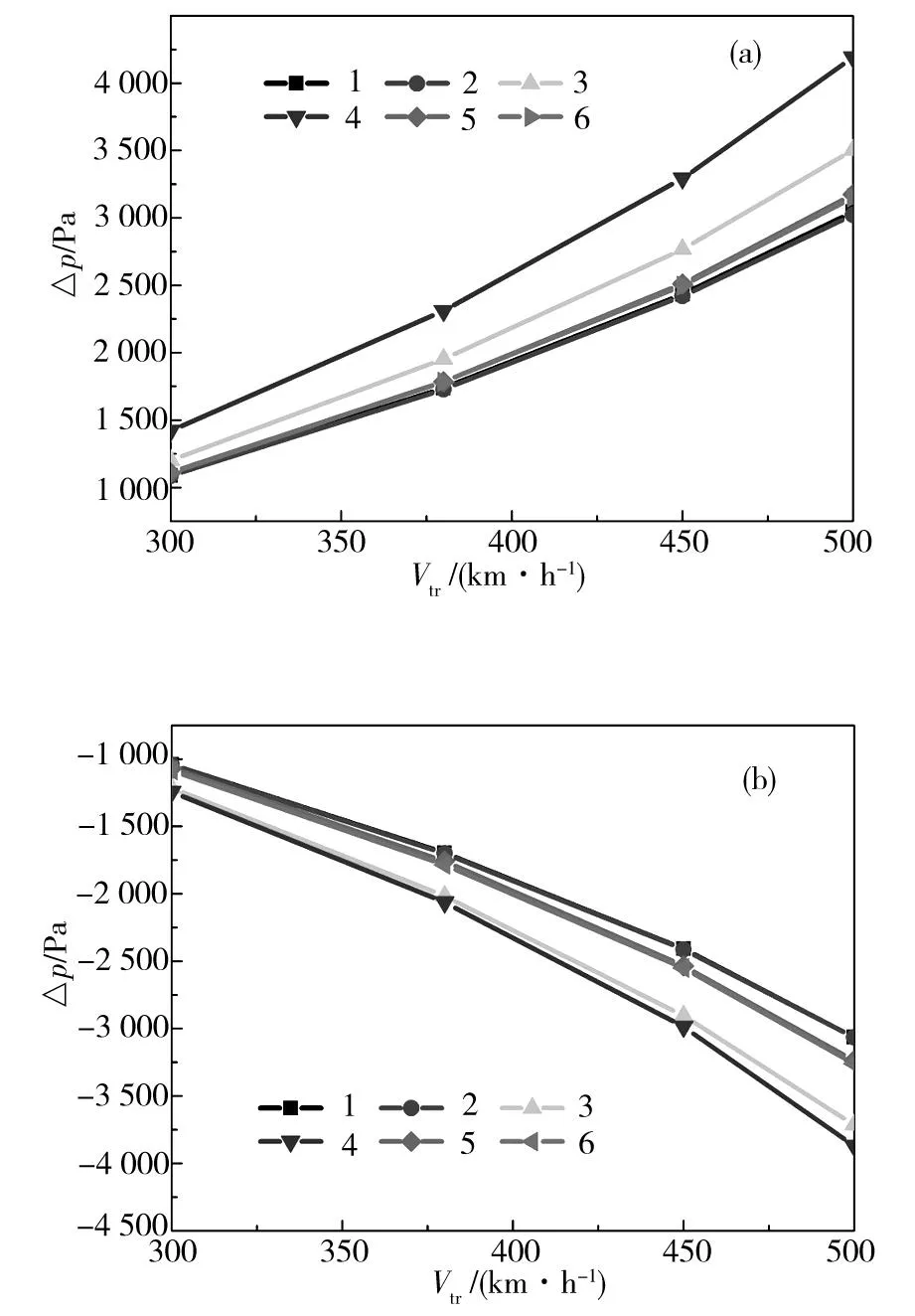
(a)正压最大值；(b)负压最大值图13　列车速度对正压最大值和负压最大值的影响特性Fig.13 Effect of the train velocity on the maximum positive pressure value and the negative pressure value in tunnel

图14为列车速度对不同断面上近车体隧道一侧的近地测点“4”的压力峰值影响。由图可见：随着车速的增加，距离隧道入口2D断面和中央断面的正压最大值也随之增加，而在距隧道出口2D处的断面上，当速度增加到一定程度，正压最大值反而下降；负压最大值随着车速的增加而增加。当列车速度为300 km/h时，正压最大值出现在隧道中央断面处，而在速度为380，450及500 km/h时，正压最大值均出现在隧道内距离隧道入口2D处，负压最大值则均出现在隧道的中央断面处。

(a)正压最大值；(b)负压最大值图14　列车速度对正压最大值和负压最大值的影响特性Fig.14 Effect of the train velocity on the maximum positive pressure and the negative pressure in tunnel of different cross-sections

3结论

1)揭示了隧道内压力波形成的过程。在复线隧道内同一断面上，隧道中央顶部的压力与其断面平均压力的变化基本相同，压力值也基本相同。

2)对于距隧道入口较近的断面上，当列车通过时，不同测点间的压力差异较大，三维流动效应明显；而在距离隧道入口较远的断面和距离出口较近的断面上，不同测点间的压力差异不大，差异主要是由列车头部和尾部通过带来的。并且根据每个断面上测点的压力值对比发现，由于受到列车周围流场和隧道壁面、地面效应的多重影响，其正压最大值和负压最大值均出现在靠近车体的地面附近。

3)车速越高，距离隧道入口较近断面上的正压最大值也越大，而在距离出口较近的断面上，当列车速度增加到一定程度上，正压最大值反而减小。

4)随着车速的增加，正压最大值多出现在距离隧道入口较近处，而负压最大值则出现在隧道的中央处。

参考文献:

[1] Ahmed S R, Gawthorpe R G. Aerodynamics of road and rail vehicles[J]. Vehicle System Dynamics, 1985(14):319-392.

[2] Raghunathan R S, Kim H D, Setoguchi T. Aerodynamics of high -speed railway train [J]. Progress in Aerospace Sciences, 2002(38):469-514.

[3] 王建宇. 列车通过隧道时诱发的空气动力学问题和高速铁路隧道设计参数[J]. 世界隧道, 1995(1): 3-13.

WANG Jianyu. Train induced by tunnel aerodynamic problems and high-speed railway tunnel design parameters[J]. World Tunnel, 1995(1): 3-13.

[4] Gawthorpe R G. Pressure effects in railway tunnels[J]. Rail International, 2000(4):10-17.

[5] 田红旗. 列车空气动力学[M]. 北京: 中国铁道出版社, 2007.

TIAN Hongqi. Train Aerodynamics[M]. Beijing: China Railway Press, 2007.

[6] 刘堂红, 田红旗. 不同外形列车过隧道实车试验的比较分析[J]. 中国铁道科学, 2008, 29(1)：51-55.

LIU Tanghong, TIAN Hongqi. Comparison analysis of the fullscale train tests for trains with different shapes passing tunnel[J]. China Railway Science, 2008，29(1)：51-55.

[7] 周亚宇. 高速列车通过合武铁路湖北段隧道空气动力性能测试[J]. 铁道建筑,2011(4):73-76.

ZHOU Yayu. Aerodynamic test of high-speed railway tunnels in Hubei section of Hefei Wuhan railway[J]. Railway Engineering, 2011(4):73-76.

[8] 赵有明, 马伟斌, 程爱君,等. 高速铁路隧道气动效应[M]. 北京：中国铁道出版社, 2012.

ZHAO Youming, MA Weibin, CHENG Aijun, et al. High-speed railway tunnel aerodynamic effect[M]. Beijing: China Railway Press, 2012.

[9] 余南阳. 高速铁路隧道压力波数值模拟和模型试验研究[D]. 成都: 西南交通大学, 2004.

YU Nanyang. Study on numerical simulation of high-speed railway tunnel pressure wave and the model test[D]. Chengdu: Southwest Jiaotong University, 2004.

[10] 王英学, 高波, 朱丹,等. 高速铁路隧道空气动力效应控制技术[M].北京：科学出版社，2012.

WANG Yingxue, GAO Bo, ZHU Dan, et al. The control technology on aerodynamics effect of high-speed railway tunnel[M]. Beijing: Science Press,2012.

[11] 梅元贵, 周朝晖, 许建林. 高速铁路隧道空气动力学[M]. 北京: 科学出版社, 2009.

MEI Yuangui, ZHOU Chaohui, XU Jianlin. Aerodynamics of high-speed railway tunnel[M]. Beijing: Science Press, 2009.

[12] Ogawa T, Fuji K. Numerical investigation of three-dimensional compressible flows induced by a train moving into a tunnel[J]. Computers and Fluids, 1997, 26(6): 565-585.

[13] Chang-Hoon Shin, Warn-Gyn Park. Numerical study of flow characteristics of the high speed train entering into a tunnel[J]. Mechanics Research Communications,2003(30): 287-296.

[14] 张雷, 杨明智, 张辉,等.高速铁路隧道洞门对隧道空气动力效应的影响[J]. 铁道学报,2013,35(11):92-97.

ZHANG Lei, YANG Mingzhi, ZHANG Hui, et al. Influence of tunnel portals on tunnel aerodynamic effects in operation of high-speed railways[J]. Journal of the China Railway Society, 2013,35(11):92-97.

[15] 王一伟, 杨国伟, 黄晨光. 高速列车通过隧道时气动阻力特性的CFD仿真分析[J]. 中国铁道科学,2012,33(增刊):33-38.

WANG Yiwei, YANG Guowei, HUANG Chenguang. CFD simulation analysis on the aerodynamic drag characteristics of high-speed train running through tunnel[J]. China Railway Science, 2012,33(Supplement):33-38.

[16] 赵晶, 李人宪, 刘杰.高速列车隧道内等速会车时气动作用力的数值模拟[J]．铁道学报，2010，32(4)：27-32．

ZHAO Jing, LI Renxian, LIU Jie. Numerical simulation of aerodynamic forces of high-speed trains passing each other at the same speed through a tunnel[J]. Journal of the China Railway Society, 2010，32(4)：27-32．

[17] 施成华, 杨伟超, 彭立敏,等.高速铁路隧道空气动力效应对水沟盖板稳定性的影响研究[J]. 铁道学报,2012,34(1):103-108.

SHI Chenghua, YANG Weichao, PENG Limin, et al. Study on aerodynamic influence on stability of ditch covers in high-speed railway tunnels[J]. Journal of the China Railway Society, 2012,34(1):103-108.

[18] 周丹. 长大隧道、隧道群空气动力效应算法研究及应用[D]. 长沙: 中南大学, 2007.

ZHOU Dan. Research on the long tunnel and tunnel groups aerodynamic alogorithm and its application[D]. Changsha: Central South University, 2007.

[19] CD-adapco Group. STAR-CD version 4.08 methodology[M]. Computational Dynamics Limited, 2008.

Numerical simulation of pressure wave characteristics generated

by a high-speed train passing through a double-track tunnel

LIU Xixian, GUO Anning, MEI Yuangui, XU Jianlin, LI Shian, ZHOU Chaohui

(College of Mechanical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

Abstract：The CFD method with finite volume method and arbitrary sliding interface moving mesh technology employed was utilized to conduct numerical investigation of the tunnel pressure waves induced by a high-speed train passing through a tunnel. In order to avoid unreasonable numerical physical phenomena, smooth start technology was used. After the validation, three-dimensional unsteady compressible turbulent flow model was adopted to study the formation of the pressure wave in tunnels. The formation process of the pressure wave was revealed, and its characteristics in different cross sections and measuring points were obtained. It shows that the pressure excursion is different in different cross sections near the portals of the tunnel yield by the three-dimensional effect of the initial compression wave. And the maximum positive pressure value also increases with the increase of train velocity. But the maximum positive pressure value decreases near the exit portal of the tunnels when the train velocity increases to a certain range. The maximum positive pressure value always appears near the entry portal of the tunnel, while the maximum negative pressure value occurs near the central section along with the tunnel.

Key words：high-speed railway; double-track tunnel; pressure wave; numerical simulation

中图分类号：U298.1

文献标志码：A

文章编号：1672-7029(2015)01-0020-08

通讯作者：梅元贵(1964-)，男，河南荥阳人，教授，博士，从事列车空气动力学研究；E-mail：meiyuangui@163.com

基金项目：国家自然科学基金资助项目(51065013)；国家重点基础研究发展规划(“973计划”)项目(2011CB711101)

*收稿日期：2014-07-24