计及风电不确定性的配电网无功模糊优化

王 进，刘 娇，陈加飞，许一帆，唐 浩，杨芳华

（1.长沙理工大学电气与信息工程学院，长沙410114；2.湖南省电力公司凤滩水力发电厂，怀化419699）

随着全球能源危机的日渐严重以及生态环境的日益恶化，风能作为最具发展潜力的可再生清洁能源，其发电技术得到了快速发展。风电机组并网后，由于其输出功率具有很强的随机性和间歇性，增加了配电网中的不确定性[1]，导致传统无功优化在考虑风电的配电网中具有一定局限性，从而对传统无功优化技术提出了新的挑战。如何解决风电并网带来的不确定性是配电网无功优化的核心问题。目前国内外学者已针对此问题进行了一定的研究。

文献[2-3]假设风电机组输出功率为一确定值，并将风电机组并网节点作为一个PQ（V）节点参与无功优化，但没有考虑风电机组输出功率的随机性；文献[4]根据配电网某日的负荷变化曲线和分布式发电容量系数特性曲线，选取了其中有代表性的3 个时间点进行分析，但每个时间点分布式发电的输出功率也为一确定值；文献[5-6]根据风电机组的功率特性曲线求出在一定风速条件下风电机组的输出功率，将风电的不确定性量化成确定性问题处理，但此方法建立的无功优化模型无法反映风电机组输出功率变化的快速性，适应性不强；文献[7-8]采用场景分析法来描述风电机组输出功率的随机性，利用风速的威布尔分布计算各典型场景发生的概率，建立全场景下的无功优化模型，仿真结果验证了该模型能够较好地适应风电机组输出功率的随机变化。但都采用威布尔分布近似描述风速的概率分布，而威布尔分布通常适用于描述风速的年平均分布情况，不适合用于描述风速的日平均分布。

考虑到风电机组输出功率的随机性以及风速概率分布的时变特性，本文利用风速预测值和预测误差估计实际风速的概率分布，并结合风电机组功率特性计算各典型场景的功率和概率，建立全场景下的以有功网损最小和静态电压稳定裕度最大为目标函数的无功优化模型。引入模糊集理论将确定性问题模糊化，进而利用最大满意度法将多目标模型转换成单目标模型。并采用量子行为粒子群优化QPSO（quantum-behaved particle swarm optimization）算法[9]对模型进行求解，该算法具有控制参数少、全局收敛性好的特点。最后，采用IEEE69 节点系统进行了仿真，验证了模型和算法的有效性。

1 风电机组的场景选取

风速的波动性使得风电场输出功率具有不确定性，风电机组功率特性（风速和风电功率的函数关系）可近似由以下分段函数表示为

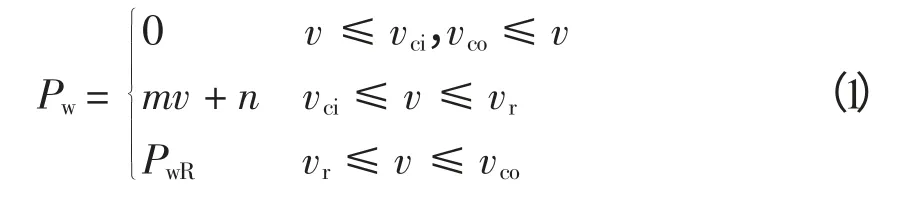
从式（1）可以得出：①当风速低于切入风速或者高于切出风速时，风机输出功率为0；②当风速高于切入风速且低于额定风速时，风机输出功率与风速的大小有关系；③当风速高于额定风速且低于切出风速时，风机以额定功率输出；因此，可将风电机组输出功率分为3 种典型场景：零输出场景、欠额定输出场景和额定输出场景。

由于场景的选取和当地风速的分布密切相关，所以计算场景概率的前提是已知当地风速的概率分布。通常的做法是根据风速的统计特性假设风速服从威布尔分布，结合风电机组的功率特性计算出各个场景的概率。威布尔分布通常只适用于描述年平均风速的分布情况，而无功优化方案的制定需利用风速/风电的预测估计出未来具体某一时刻或某一天的风电出力参考值，所以在无功优化问题中，利用风速预测值和预测误差估计的风速概率分布计算场景概率更合理些。

由于风速的随机性，风速预测总会存在误差，因此，可根据风速预测值和预测误差来估计实际风速的概率分布情况。文献[10]表示可以将风速预测误差Δv 看作一个随机变量，且服从均值为0、标准差为σv的正态分布。因此，在有风速预测的基础上，实际风速的概率密度函数为

结合式（1）和式（2）可推导出3 种典型场景的概率计算公式。零输出场景的概率λ1为

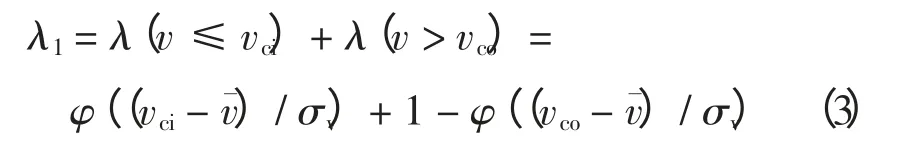
欠额定输出场景的概率λ2为

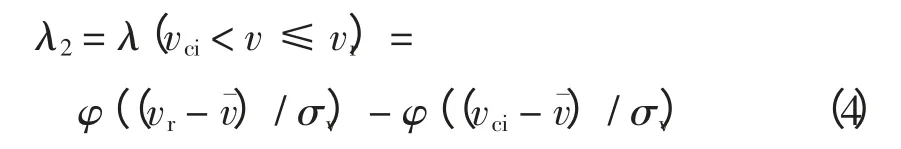
额定输出场景的概率λ3为

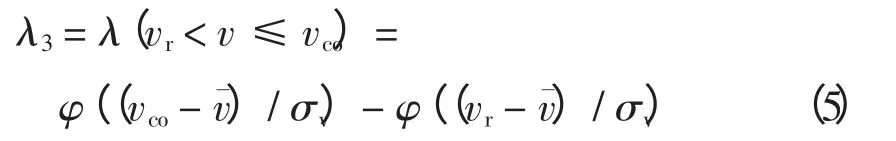
式中，φ（x）为标准正态分布的概率密函数。此处可以使用标准正态分布进行查表计算。

零输出场景和额定输出场景的风机输出功率分别为0、额定功率，欠额定输出场景的功率则为相应风速范围内风机功率的期望值。

2 含风电机组的配电网双目标无功优化模型及其模糊化

2.1 目标函数

本文建立的无功优化模型同时考虑了电网运行的经济性和稳定性，以有功网损Ploss最小和静态电压稳定裕度K 最大为目标函数，并选择无功补偿设备的投入组数NC 为控制变量，负荷节点电压U 作为状态变量。

（1）电网有功功率损耗Ploss为

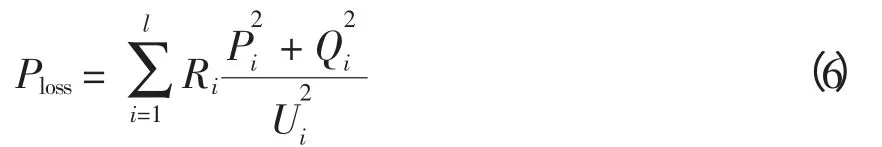
式中：l 为配电网支路数；Ri为支路i 的电阻；Ui、Pi和Qi分别为支路i 的末端节点电压、注入的有功功率和无功功率。

（2）衡量配电系统静态电压稳定裕度K 的指标有很多，本文选择基于潮流计算的稳定性指标[11]来表示K，其表达式为

式中：Lij为支路ij（i 和j 分别为首端和末端节点）的电压稳定性指标；L 为所有支路中Lij的最大值；Rij和Xij分别为支路ij 的电阻和电抗；Pj和Qj分别为注入支路末端节点j 的有功和无功功率；Ui为首端节点i 的电压。

由式（7）可知，静态电压稳定裕度最大等价于电压稳定性指标最小。所以建立的多目标无功优化目标函数为

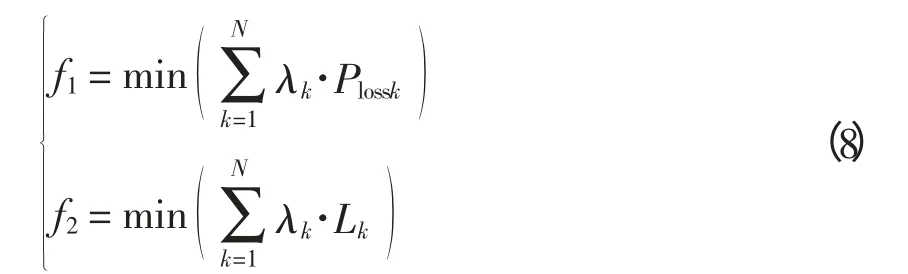
式中：N 为风机输出功率的场景数；λk为第k 个场景的场景概率；Plossk和Lk分别为电网在第k 个场景下的有功功率损耗和电压稳定指标。

2.2 约束条件

各个节点功率等式约束条件为

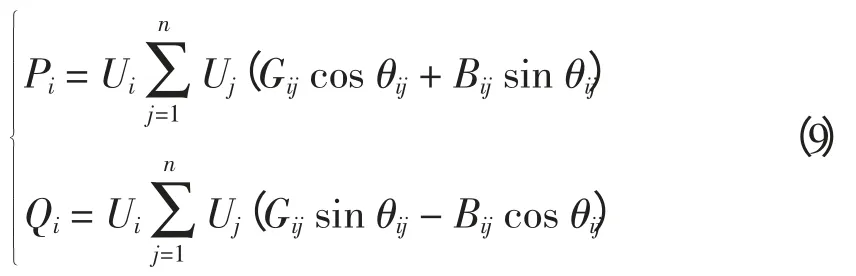
式中：Pi和Qi分别为注入节点i 的有功和无功功率；Gij和Bij分别为支路电导和电纳；θij为节点i 与节点j 电压相位差。

不等式约束条件为

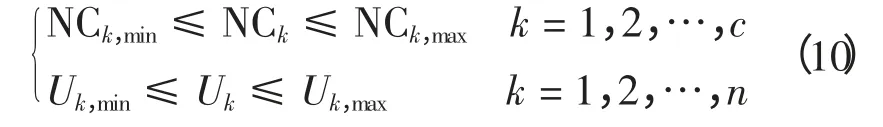
式中：c 为无功补偿节点数；NCk，max和NCk，min分别为补偿电容器组数的上、下限；n 为节点数；Uk，max和Uk，min分别为节点k 的电压上、下限。

2.3 双目标配电网无功优化模型的模糊化

由于有功网损和电压稳定性指标两个单目标的量纲不一致，并且相互之间可能存在矛盾，为协调不同目标之间的关系，可以采用最大满意度法将两个优化子目标转化为单一目标，转换的关键是隶属度函数的确定。网损和电压稳定性指标越小越好，有上限而无下限，因此选择降半形的隶属度函数。而降半矩形分布是二点分布，不适合求解连续性的优化问题，故选择降半г 形分布为隶属度函数。各子目标的隶属度函数[12]为

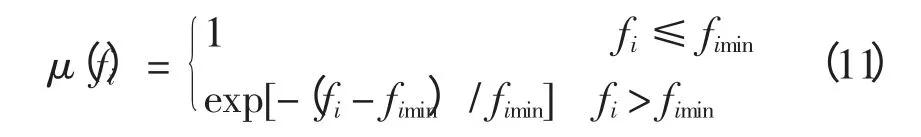
式中：fimin为单目标函数fi在约束条件下的最小值；i=1，2；0〈μ（fi）≤1。

引入模糊隶属度函数后，根据最大满意度准则，将模糊的多目标优化问题转化为单目标优化问题，则配电网的无功优化模型可描述为

式中：μ 为总体满意度，μ = min{μ（f1），μ（f2）}；网损越小（μ（f1）越接近于1），电压稳定性指标越小（μ（f2）越接近于1），则总体满意度μ 值越接近于1。表示优化方案的效果就越好。

模型具体的转换过程为：输入系统数据，分别求解以网损期望值和电压稳定性指标期望值最小为目标函数的单目标优化模型，得到最优网损期望值f1min和最优电压稳定性指标期望值f2min；将f1min和f2min分别代入式（11），得到两个子目标的隶属函数表达式，按照最大满意度准则将原始模型转换成式（12）的单目标模型。

3 基于QPSO 算法的含风电机组配电网无功优化

3.1 QPSO 算法的基本原理

针对粒子群算法不能保证全局收敛[13]的缺点，孙俊等人以量子力学为背景，提出了一种基于δ 势阱的QPSO 算法。该算法中每一个粒子都具有量子行为且只有位置向量，粒子的状态用波函数（其物理意义为：波函数的平方是粒子在搜索区域某一位置出现的概率密度）来描述；粒子在迭代过程中没有确定的轨迹，能够以某一概率出现在整个可行的搜索区域中任何一个位置。所以QPSO 算法是全局收敛的。

为了保证算法的收敛性，每一个粒子必须收敛于各自的局部吸引因子。为了保证粒子的聚集性，在局部吸引粒子的每一维上建立一个一维δ 势阱模型。求解粒子在δ 势阱的定态薛定谔方程得到粒子的波函数，从而得出粒子在搜索区域某一位置的概率密度函数，然后采用蒙特卡罗模拟的方法得到粒子位置X 的进化公式为

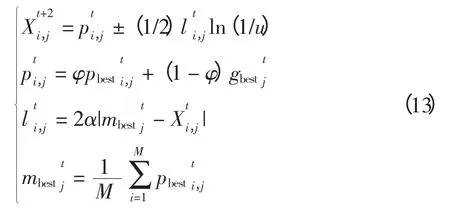
式中：i，j 表示粒子i 的第j 维；t 为当前迭代次数为粒子的吸引粒子为δ 势阱的特征长度分别为全局最好位置和个体最好位置；α 为收缩扩张系数；φ 和u 均为区间[0，1]上均匀分布的随机数；mbest为所有粒子个体最好位置的平均值。

参数α 采取线性减少策略（在算法迭代过程中线性地减少参数α 的值）。α 的确定公式为

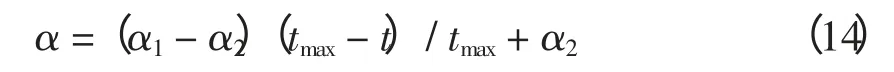
式中：α1和α2分别为参数α 在整个迭代过程中的初始值和最终值；tmax为允许最大迭代次数。

3.2 粒子个体状态向量的编码

无功补偿设备的投入组数为离散型整数控制变量，采用十进制编码方式，粒子长度即为控制变量的个数，则粒子群中粒子i 的编码格式为

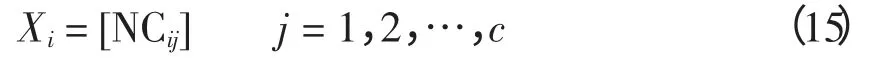
式中：NCij为第j 个无功补偿点无功补偿设备投入的组数；c 为无功补偿节点数。

在实际的配电网中，投入补偿节点的无功补偿设备组数是一个整数型变量，但是Xi在每次优化更新后都不能保证其整数特性，本文通过映射编码和取整方法对其进行处理。已知每组无功补偿设备的容量为Qav，控制变量Xij的取值范围为[0，NCmax]，粒子在该范围内初始化、位置更新后，按式（16）所示，将Xij转化为相应的无功补偿容量值代入目标函数进行计算（round（）为取整函数）：

3.3 算法流程

基于QPSO 算法的含风电机组的配电网无功模糊优化流程如图2 所示。

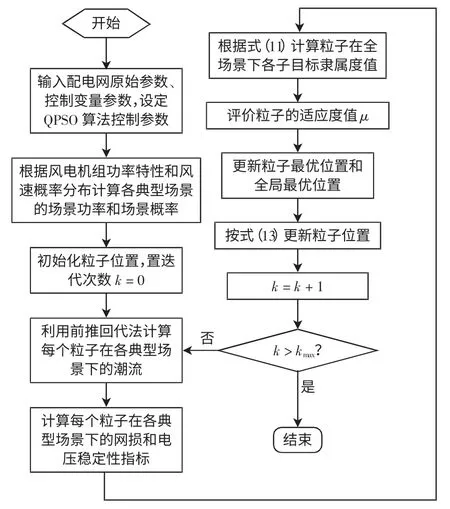
图1 基于QPSO 算法的计算流程Fig.1 Flow chart based on QPSO algorithm

4 算例分析

4.1 仿真系统及数据

以图2 所示的IEEE69 节点辐射状配电系统为算例，支路参数和节点数据见文献[14]。系统功率基准值为1 MVA，电压基准值为12.66 kV。通过潮流计算得出各个节点的无功裕度[15]，选取节点12、20、27、42、50 和54 为无功补偿点，每处安装有可投切电容器组，单组电容器容量均为50 kvar，各处可投切电容器组最多为10 组。节点54 接入一台额定容量为600 kW 的异步风电机组，切入风速、额定风速和切出风速分别为5 m/s、8 m/s 和22 m/s。系统节点电压取值范围为0.95～1.05。量子行为粒子群算法的控制参数为：种群规模为40；最大迭代次数为100；α1=0.5；α2=1.0。

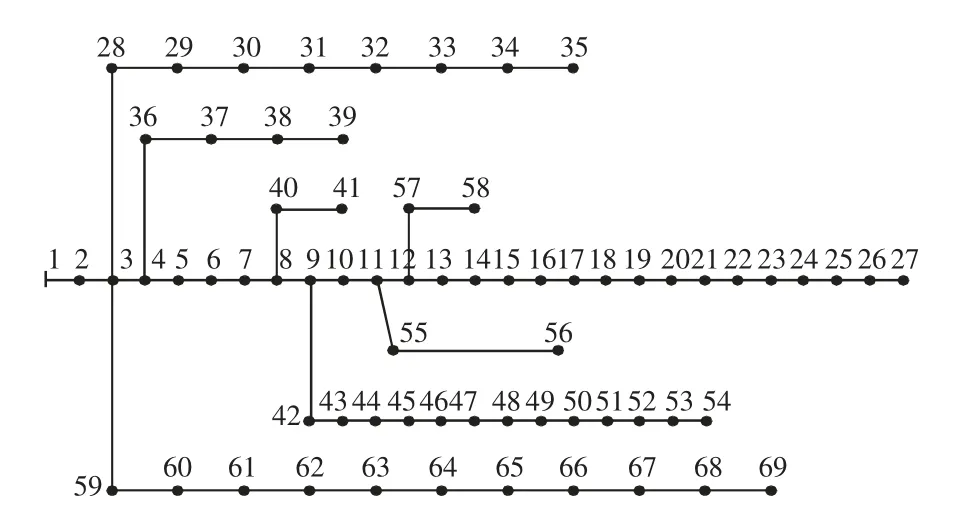
图2 IEEE69 节点配电系统Fig.2 Configuration of IEEE 69-bus distribution system

采用支持向量机法对该地区某日的风速进行短期预测，平均相对误差为10%。选取5 个典型的时刻进行分析，其对应的预测误差及其概率分布如表1 所示。

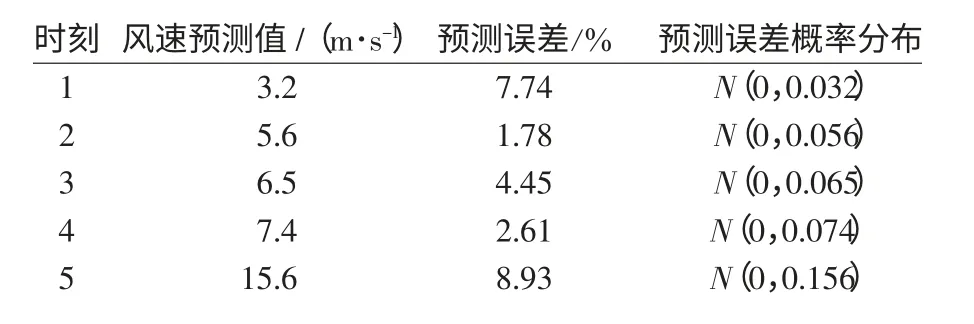
表1 风速预测数据Tab.1 Predicted data of wind speed

4.2 仿真结果

采用论文提出的模型和算法对表1 中5 个典型时刻分别进行无功优化，各个时刻无功优化方案和无功优化结果分别如表2 和表3 所示。

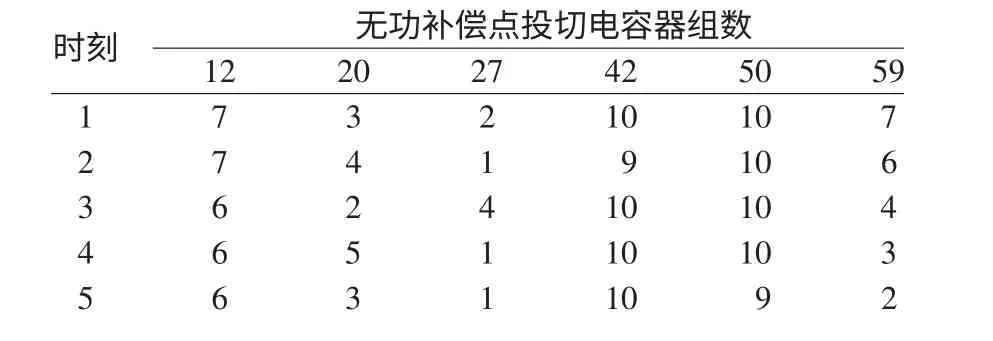
表2 各典型时刻无功优化方案Tab.2 Schemes of reactive power optimization in typical moment

表3 各典型时刻无功优化结果Tab.3 Results of reactive power optimization in typical moment

对典型时刻4 进行进一步测试，测试分为3个典型场景：零场景、欠额定场景和额定场景，各场景的功率分别为：0、215.3 kW 和600 kW，按式（3）～（5）计算出各场景的概率分别为：0.139、0.466和0.395。测试考虑了以下3 种情况：方案1、2 和3分别是以网损期望隶属度值最大、电压稳定指标期望隶属度值最大和总体满意度最大为目标时，在全场景下的最优无功优化方案。详细优化方案和结果分别见表4 和表5。

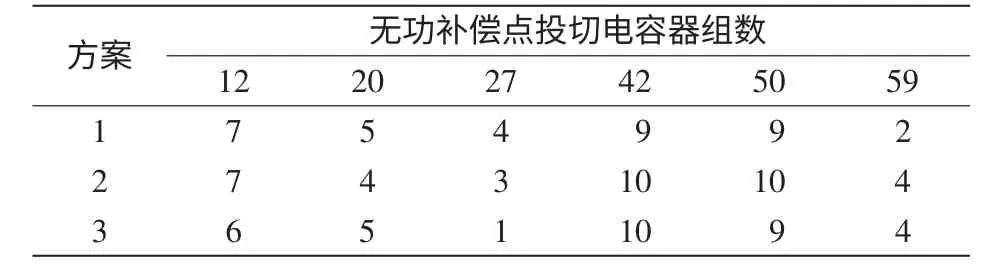
表4 预测风速为7.4 m/s 时的无功优化方案Tab.4 Scheme of reactive power optimization with the predicted wind speed 7.4 m/s

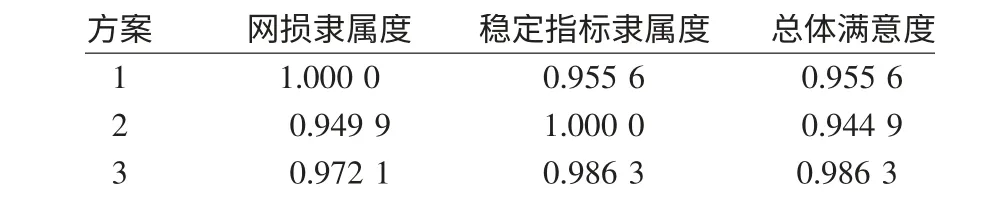
表5 预测风速为7.4 m/s 时的无功优化结果Tab.5 Result of reactive power optimization with the predicted wind speed 7.4 m/s

4.3 分析讨论

从表2 可看出，各典型时刻的无功优化方案区别较大，若不考虑风速概率分布的时变特性，而只采用威布尔分布近似描述一天中各时刻风速的概率分布，则风电机组运行在时刻1 和时刻5 时会出现节点电压最小值越限的情况，可见在制定无功优化方案的过程中，不适合采用威布尔分布近似描述风速的日平均分布或者某个时刻的概率分布。因此本文建立的场景模型对一天中风机输出功率的随机变化具有更好的适应性。

从表3 可以看出，风电机组的接入对网损和电压稳定性指标都具有一定程度的改善作用。以时刻5 为例，初始网络（未接入风电机组，未进行无功补偿）的网损为227.837 8 kW，电压稳定性指标为0.091 6，最低电压为0.908 p.u.，接入风电机组且安装无功补偿设备之后网络的网损为77.401 5 kW，电压稳定性指标为0.038 2，最低电压为0.952 p.u.。可见风电机组的接入和充足的无功补偿容量能大大地降低配电网网损和电压稳定性指标，提高电压水平和电能质量。

从表5 可以看出，进行单目标优化时（方案1和方案2），每次优化都能使优化子目标的隶属度达到1，但另外一个子目标的隶属度则相对较低，从而总体满意度不是很好。比如方案1，虽然决策者对配电网网损优化结果完全满意，然而此时电压稳定指标相对较大，可能达不到决策者的要求。当进行多目标优化时（方案3），虽然各子目标不是最优，但每个子目标都有相对较高的隶属度，很好地协调了各子目标之间的关系，总体满意度比较高，达到了整体优化的效果。

综合上述结果可得出，本文建立的模型计及了风电机组输出功率的不确定性和风速概率分布的时变特性，兼顾了系统的经济性和安全性，更符合系统实际应用情况。仿真结果表明该模型对一天中风机输出功率的随机变化具有更好的适应性，且能很好地协调系统经济性和安全性之间的关系。因此该模型在解决含风电机组的配电网无功优化问题中具有一定的实用性。

5 结语

本文针对风电并网给配网无功优化带来的不确定性，提出了基于风速预测的场景分析法，更好地反映了风电机组输出功率的随机性。

综合考虑配电网运行的经济性和安全性，根据模糊集理论和最大满意度准则将多目标优化问题转换成单目标优化问题，并用QPSO 算法进行求解。多目标转换很好地协调各子目标之间的关系，实现过程简单，且避免了对决策者经验的依赖，从而减少了因决策者经验不足而造成的损失，更加符合无功优化的实际应用；QPSO 算法全局收敛性好，并且控制参数调节简单，提高了优化效率。

该模型及方法适用于日前调度计划安排，对配电网未来一天24 时段动态无功优化方案的制定具有一定的参考价值和实际指导意义。

[1]白鸿斌，王瑞红（Bai Hongbin，Wang Ruihong）. 风电场并网对电网电能质量的影响分析（Influence of the gridconnected wind farm on power quality）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2012，24（1）：120-124.

[2]魏希文，邱晓燕，李兴源，等（Wei Xiwen，Qiu Xiaoyan，Li Xingyuan，et al）. 含风电场的电网多目标无功优化（Multi-objective reactive power optimization in power system with wind farm）[J]. 电力系统保护与控制（Power System Protection and Control），2010，38（17）：107-111.

[3]Niknam T.A new approach based on ant colony opti-mization for daily volt/var control in distribution networks considering distributed generators[J].Energy Conversion and Management，2008，49（12）：3417-3424.

[4]杨广杰，郑华（Yang Guangjie，Zheng Hua）.含分布式电源的配电网电压无功优化问题研究（Research on the voltage and reactive power optimization control of distribution system with distributed generations）[J]. 现 代 电 力（Modern Electric Power），2012，29（2）：27-31.

[5]赵晶晶，符杨，李东东（Zhao Jingjing，Fu Yang，Li Dongdong）.考虑双馈电机风电场无功调节能力的配电网无功优化（Reactive power optimization in distribution network considering reactive power regulation capacity of DFIG wind farm）[J]. 电力系统自动化（Automation of Electric Power Systems），2011，35（11）：33-38.

[6]陈琳，钟金，倪以信，等（Chen Lin，Zhong Jin，Ni Yixin，et al）.含分布式发电的配电网无功优化（Optimal reactive power planning of radial distribution systems with distributed generation）[J].电力系统自动化（Automation of Electric Power Systems），2006，30（14）：20-24.

[7]陈海焱，陈金富，段献忠（Chen Haiyan，Chen Jinfu，Duan Xianzhong）. 含风电机组的配网无功优化（Reactive power optimization in distribution system with wind power generators）[J]. 中国电机工程学报（Proceedings of the CSEE），2008，28（7）：40-45.

[8]何禹清，彭建春，毛丽林，等（He Yuqing，Peng Jianchun，Mao Lilin，et al）. 含多个风电机组的配电网无功优化（Reactive power optimization in distribution system with multiple wind power generators）[J]. 电 力 系 统 自 动 化（Automation of Electric Power Systems），2010，34（19）：37-41.

[9]Sun Jun，Fang Wei，Wang Daojun，et al. Solving the economic dispatch problem with a modified quantum-behaved particle swarm optimization method[J]. Energy Conversion and Management，2009，50（12）：2967-2975.

[10]Lange M. On the uncertainty of wind power predictionsanalysis of the forecast accuracy and statistical distribution of errors[J]. Journal of Solar Energy Engineering，2005，127（2）：177-184.

[11]刘学平，刘天琪，王剑（Liu Xueping，Liu Tianqi，Wang Jian）. 基于小生境的配电网多目标分布式电源规划（Niche-based multi-objective distributed generators planning in distribution network）[J].电网技术（Power System Technology），2010，34（10）：126-130.

[12]丘文千（Qiu Wenqian）.多目标电力系统无功优化及其方法（Multi-objective reactive power optimization and its approaches）[J].南方电网技术（Southern Power System Technology），2010，4（5）：66-70，78.

[13]张斌（Zhang Bin）.基于粒子群算法的配电网无功补偿优化规划（Reactive power compensation of distribution network based on particle swarm optimization）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2010，22（2）：157-160.

[14]刘健，毕鹏翔，董海鹏，等.复杂配电网简化分析与优化[M].北京：中国电力出版社，2002.

[15]刘传铨，张焰（Liu Chuanquan，Zhang Yan）.电力系统无功补偿点及其补偿容量的确定（Confirmation of reactive power compensation node and its optimal compensation capacity）[J].电网技术（Power System Technology），2007，31（12）：78-81.