上海某220 kV地下变电站基坑工程优化设计

刘 漾姜 波马晓元霍晓波

（1同济大学地下建筑与工程系，上海200092；2上海电力设计院有限公司，上海200025）

上海某220 kV地下变电站基坑工程优化设计

刘 漾1，姜 波2马晓元2霍晓波1

（1同济大学地下建筑与工程系，上海200092；2上海电力设计院有限公司，上海200025）

摘 要以上海地区某220 kV地下变电站基坑工程为基础，采用启明星及Plaxis进行数值模拟，结合与已建基坑工程进行类比的方法，分析了地下连续墙的插入比、坑内加固参数（加固深度、宽度、厚度及抽条加固置换率）对基坑稳定性、安全系数、墙体位移及墙体内力等的影响，得到如下结论：①基坑的最优插入比可选定在0．75～0．8之间；②基坑坑内被动区土体加固优化方案为加固深度17．1 m，加固厚度11 m，加固宽度3 m，抽条加固置换率0．3。

关键词基坑，地下变电站，优化设计，数值分析，工程类比

Optim ization Design of a 220 kV Underground Substation Excavation in Shanghai

LIU Yang1，JIANG Bo2MA Xiaoyuan2HUO Xiaobo
（1 Department of Geotechnical Engineering，Tongji University，Shanghai 200092，China；2 Shanghai Electric Power Design Institute，CO．，Ltd．，Shanghai 200025，China）

Abstract A series of parametric studies for a 220 kV underground substation excavation in Shanghai area were performed with the two-dimensional finite element code Qimstar and Plaxis．The results were compared with the local historical cases to investigate the effects of the penetration ratios and the reinforcement parameters（i．e．，reinforcement depth，width，thickness and replacement ratio of strip strengthening soil）on the stability of excavations，safety factors，displacements and internal forces of diaphragm walls．On the basis of the numerical analysis results，some major findings were obtained：（1）the optimization penetration ratio was between 0．75 to 0．8；（2）the optimization strengthening scheme of soil was that the strengthening depth，strengthening thickness and the width of strengthening soil，and the replacement ratio of strip strengthening soil were 17．1 m，11 m，3 m and 0．3，respectively．

Keywords excavation，underground substation，optimization design，numerical analysis，engineering analogy

1 引 言

随着城市的发展，对电力需求的持续增长，在城区建设地下变电站而带来的基坑支护工程也越来越多。基坑支护工程是集岩土工程与结构工程为一体的系统工程，涉及的影响因素多，而且各种因素之间的相互作用比较复杂［1］。在设计基坑工程时，应满足安全可靠、经济合理、技术可行、施工便利和可持续发展等技术要求［2］。为满足这些要求需要对多种方案进行力学分析，综合比较，以获得最优设计方案。

以弹性地基梁法为代表的传统基坑分析方法虽在设计中普遍应用，但不能完全、准确反映基坑工程中的力学行为，比如弹性地基梁法通常只能分析支护结构的变形，无法分析墙后土体的沉降和坑底土体的隆起变形。随着近年来有限元数值方法在岩土工程领域取得了长足的进步，连续介质模型也成功应用在基坑优化设计中，解决了传统基坑分析方法中不能反映土体与围岩相互作用以及基坑开挖空间效应的问题。

本文主要采用连续介质模型，利用启明星和Plaxis［3］进行数值模拟，并结合已建基坑工程类比的方法对上海地区典型变电站基坑的插入深度、加固方案进行优化设计，为今后类似基坑工程提供设计参考。

2 工程概况

上海某220 V地下变电站基坑开挖深度为19 m，采用厚度为1 000 mm的地下连续墙围护结构，连续墙有效长度为36 m，插入比约为0．9，采用四道混凝土围檩＋支撑，墙顶标高为±0．0 m。考虑地面超载20 kPa。

基坑采用了裙边加抽条的加固方案，加固方案如图1、图2所示。

图1　基坑加固平面图（单位：mm）Fig．1 Plan review of strengthening for the excavation（Unit：mm）

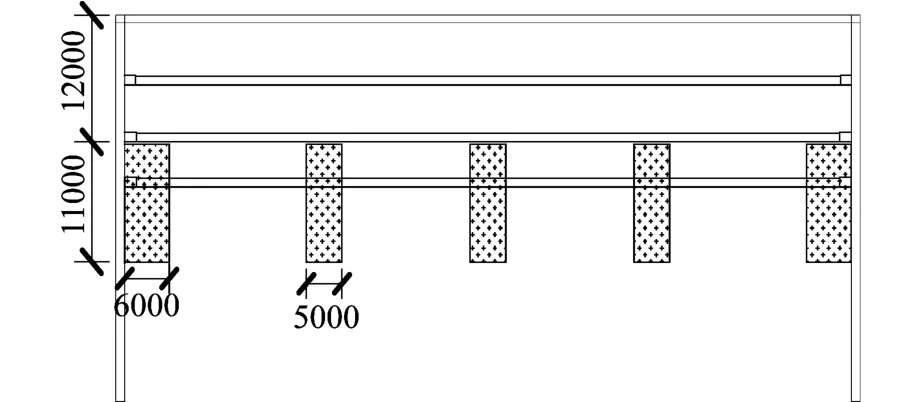
图2　基坑加固剖面图（单位：mm）Fig．2 Cross section of strengthening for the excavation（Unit：mm）

3 计算模型

计算模型如图3、图4所示。基坑开挖深度H ＝19 m。Plaxis计算模型模拟一半结构，左边界距离基坑围护结构60 m，模型二维尺寸为80 m×56 m。地表荷载取20 kPa。

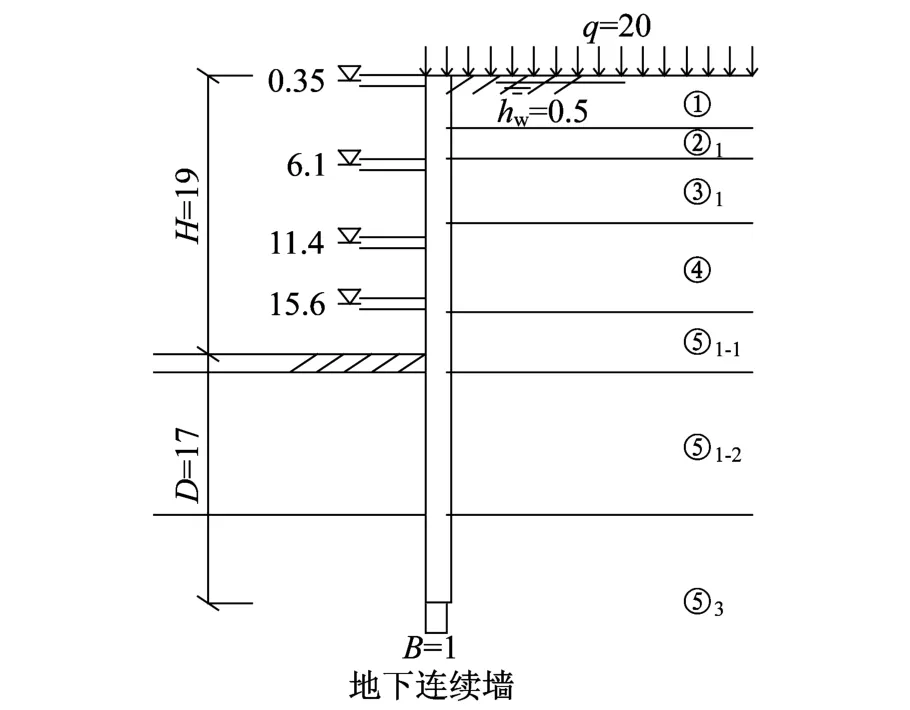
图3　启明星计算模型Fig．3 Analysis model in Qimstar

图4　Plaxis计算模型图Fig．4 Analysis model in Plaxis

模型侧面为位移边界，限制水平移动；底部为固定边界，限制水平移动和垂直移动；模型顶面为地表，取为自由边界。基坑的围护结构（地下连续墙）采用Plate单元模拟，基坑支撑采用Anchor单元模拟，土体采用HS模型。

岩土工程一般依照摩尔－库仑破坏准则来判别基坑失稳，因此，本文这样定义基坑的安全系数：

式中，c，φ为土体的强度系数；cr，φr为土体破坏的临界强度系数；Fs为基坑的安全系数。

4 计算结果分析

采用变量控制法，即在其他参数不变的情况下，改变某个设计参数研究其敏感性，获取最优值，并通过与已建基坑工程类比获取相关经验，结果如下。

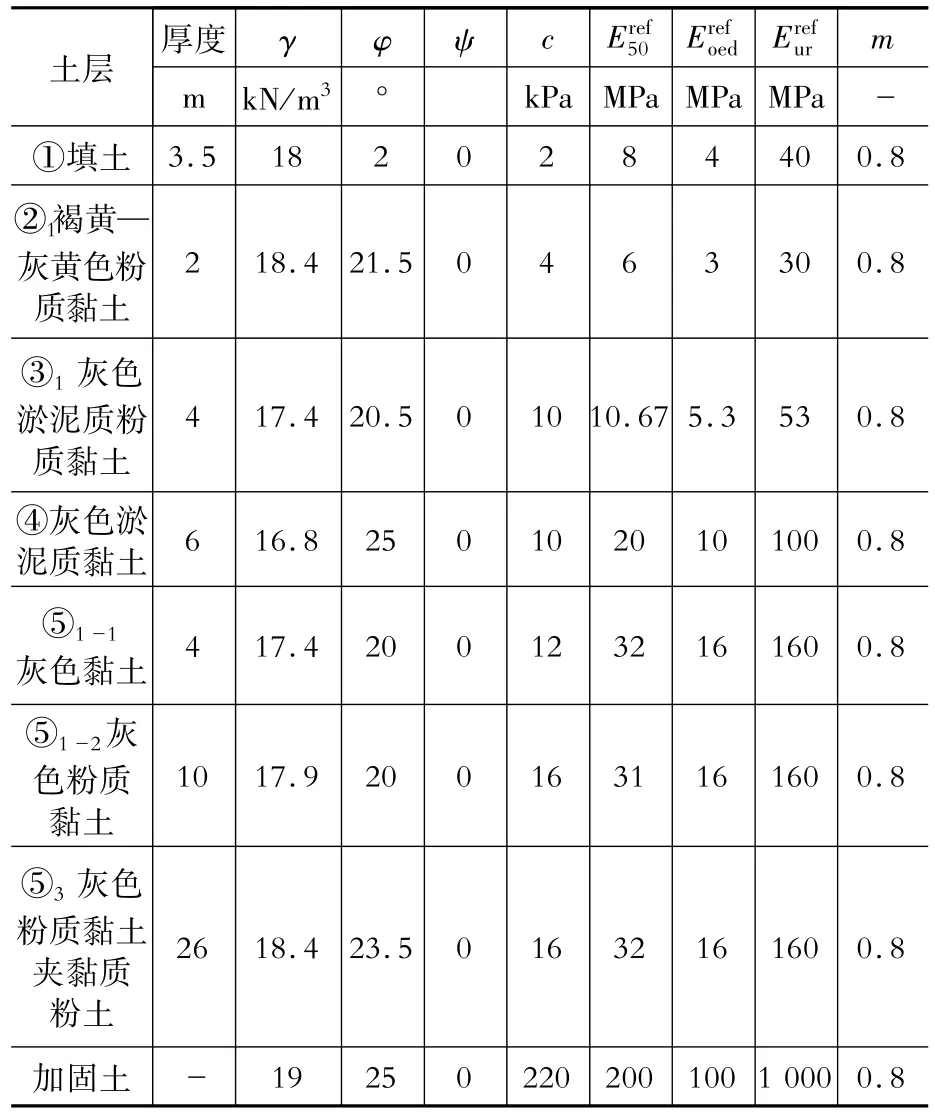
表1　模型参数取值表Table 1 Physical and mechanical parameters of soils

4．1 地下连续墙插入比的优化

选取插入比为0．4、0．5、0．6、0．7、0．8、0．9、1．0的七种情况，分别对基坑稳定性、安全系数、墙体最大位移、墙底位移、墙体最大弯矩及最大剪力进行分析比较。

不同插入比条件下基坑的稳定性如图5所示。

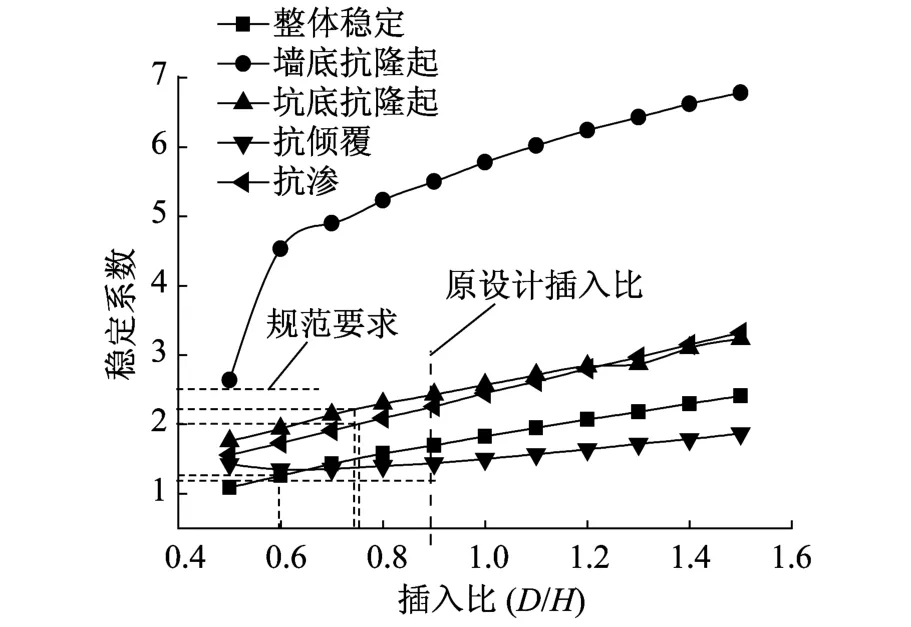
图5　不同插入比条件下稳定性校核Fig．5 Relationship between the excavation stability and the penetration ratio

由图可知，基坑的整体稳定性随插入比的增大呈线性增长趋势，而墙底抗隆起（即地基承载力）在插入比为0．6的位置发生突变，原因是此时墙底正处于两层土的交界处。依据规范［4］要求选取满足所有稳定性要求的最小插入比大约在0．75，而原设计的插入比约为0．89（17／19）。理论上，原设计可以减少围护墙插入深度达0．12 H（2．3 m），但由于墙体受力、变形以及环境保护等原因使得设计插入比取值较为保守。

不同插入比条件下基坑安全系数如图6所示，由图可知，基坑安全系数随着插入比增大呈线性增长关系，曲线没有明显的拐点出现，这一规律与启明星软件的计算结果一致，因此可以得到以下结论：从稳定性的角度分析，满足最小稳定性要求的插入比即为最佳插入比。

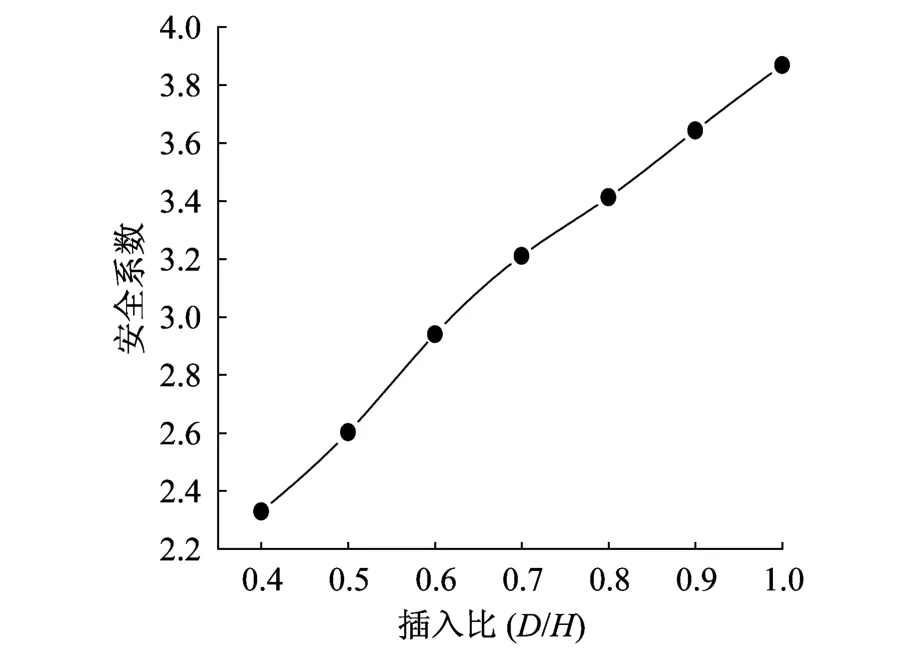
图6　不同插入比条件下安全系数Fig．6 Relationship between the safety factor and the penetration ratio

不同插入比条件下墙体最大位移如图7所示。

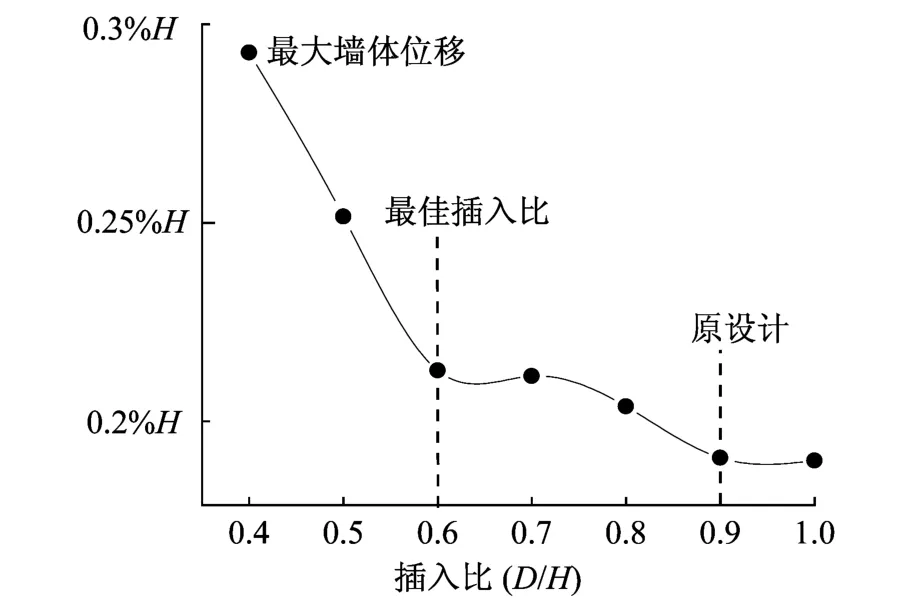
图7　不同插入比条件下墙体最大位移Fig．7 Relationship between the maximum displacement of the wall and the penetration ratios

曲线中可以很明显地看到在插入比为0．6处有一个拐点，即对于插入坑底以下0．6 H深度的墙体对围护结构自身的位移控制起很大的作用，而再深的墙体虽然对抑制墙体最大位移有一定的帮助，但其“性价比”不如前者高。因此，仅从墙体最大位移这一指标来看，0．6为最佳插入比。不同插入比条件下墙底位移如图8所示。

图8　不同插入比条件下墙底位移Fig．8 Relationship between displacement of the wall tip and the penetration ratio

由图可知，D／H＝0．7为曲线拐点。因此仅从墙底位移这一指标来看，0．7为最佳插入比。

不同插入比条件下围护墙体的最大弯矩、剪力曲线如图9所示。

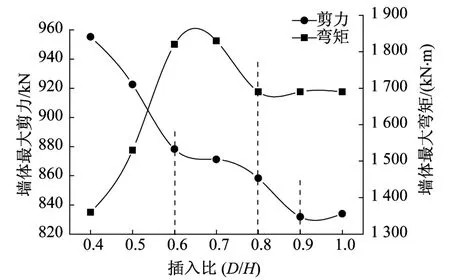
图9　不同插入比条件下墙体内力Fig．9 Relationship between internal force of the diaphragm wall and the penetration ratio

从最大弯矩控制的角度看，墙体在较小插入比的条件下弯矩水平较小，随着插入比的增大，墙体位移形态发生变化，从踢脚形态转变为中间大两边小的形态，这使得墙中（接近坑底）位置的弯矩较大，而随着插入比的继续增加，大约到0．8之后，墙体最大弯矩开始稳定。因此，从这一结论可以认为插入比为0．8时较为合适。墙体最大剪力的变化出现两个拐点，其中插入比为0．9为极小值点，考虑到控制弯矩的要求，将0．9作为剪力控制的最佳插入比。综合而言，在位移的控制条件下，0．8～0．9为比较合适的插入比范围。

以上分别从基坑稳定性、安全性、墙体位移与内力四个角度对基坑插入比进行重新优化设计，其优化结果如表2所示，墙体位移给出的建议插入比偏小，安全性没有明确的拐点及建议值，墙体最大剪力指标相比而言占最后的决策权重较轻，仅作为参考，稳定性与墙体最大弯矩作为比较重要的衡量指标最后决定了综合的插入比，最后选取0．75～0．8作为该地下变电站基坑的最优插入比，相比原设计节约了0．95～2．85 m的墙体长度。

表2　基坑建议插入比汇总Table 2 Summary of the proposed penetration ratio

通过统计上海地区类似深度的地连墙围护结构的插入比可以从经验的角度对上海地区220 kV变电站基坑的插入比进行优化，同时对上述理论分析的合理性加以评判。通过查询上海地区基坑数据库［5］，上海地区部分开挖深度在15～25 m地下连续墙围护结构的插入比信息如图10所示。

图10　不同开挖深度条件下插入比统计Fig．10 Statistics for penetration ratios of excavations with different depths

选定开挖深度（19 m）±1 m范围内1 000 mm厚地连墙的基坑案例作为分析样本（虚线划定的范围内），共有六例满足要求，其中，最大插入比为0．875而最小的则为0．66，样本均小于本工程插入比（0．9），证明原方案确实存在优化的空间。此外，在建议插入比范围内（0．75～0．8）有一例样本，另有一例样本远小于建议范围的下限，有四例样本落在0．8～0．85的区间内。

综上所述，可以得出结论：原方案插入比的确过于保守，存在优化的空间；其次，当前开挖深度在18～20 m间的民用基坑工程插入比多定为0．8～0．85间；相较于理论分析得出的结论（0．75～0．8），实际工程要相对保守一些，考虑到工程中安全储备的影响，理论分析所得出的结论是值得参考的。

4．2 基坑坑内被动区土体加固优化

在不改变加固形式的条件下对已有的加固方案细节进行优化，取长边中间位置作为计算剖面，理论上这个位置最符合平面应变状态。优化参数选取如图12所示。

4．2．1 加固深度优化

对初始加固深度h1进行优化（h1参数定义见图12，表示地面到加固区中心的距离），分别取0．61 H（11．5 m）、0．71 H（13．5 m）、0．82 H（15．5 m）、0．92 H（17．5 m）、1．03 H（19．5 m）、1．13 H（21．5 m）进行计算，并监测不同h1时最大地表沉降及最大墙体位移情况，其结果如图11所示。

图11　不同加固深度下最大坑外地表沉降及墙体位移Fig．11 Relationship between the maximum ground settlement behind the diaphragm wall and the strengthening depth

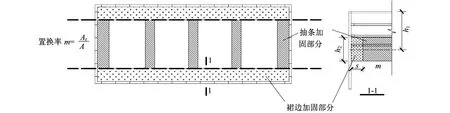
图12　基坑加固优化参数选取Fig．12 Optimization parameters of excavation strengthening

从图中可以很直观地发现当加固深度为0．9H时曲线（最大坑外沉降）出现了一个明显的拐点，加固深度为H～1．1H时的加固效果与之相比没有明显的增加，且有弱化的趋势。因此，建议将加固深度选为0．9H，这一结论与原设计十分接近。从控制墙体位移的角度看，加固深度没有明显的最优值，但在1．1 H加固深度前后墙体最大位移已有没有明显的差别，据此建议最优加固深度为1．1 H左右。在实际工程中，由于工程建设条件的区别，工程人员应根据工程主控要素来选择最优加固深度，但总体建议控制在0．95 H～1．1 H之间。

4．2．2 裙边加固宽度优化

对裙边加固宽度s进行优化，s不能单纯地理解为加固宽度的大小，没有裙边加固的区域也会采用抽条加固，因此，裙边加固与抽条加固是相互补的关系。为方便计算将s值取为0 m、2 m、4 m、8 m与10 m，但在分析中将上述数值理解为裙边宽度与抽条宽度的比值，用参数r表示。图13计算结果表明，尽管裙边加固越宽，其对坑外地表沉降及墙体位移的抑制效果越好，但所减小的沉降值相比其加固宽度的增加而言是不经济的，置换率为0．27（原设计）抽条加固已经可以达到裙边加固几乎相同的效果。因此，在原设计抽条加固置换率不降低的条件下，可以将裙边加固完全改为抽条加固。

4．2．3 加固厚度优化

分别采用不同的加固厚度（0．37 H、0．47 H、0．58 H、0．68 H、0．79 H）进行计算分析，计算结果如图14所示。

图13　最大坑外沉降、墙体位移与r的关系Fig．13 Relationship between largest settlement of ground outside the excavation／displacement of the wall and r

图14　最大坑外沉降、墙体位移与加固厚度关系Fig．14 Relationship between the largest settlement of ground outside the excavation／displacement of the wall and the thickness of strengthening

从图中可见，坑外最大沉降与墙体最大位移随坑内加固厚度的增大近似线性减小，因此对于此基坑工程不存在最经济的加固厚度，即需要控制多少位移，就应增加等比例的厚度。

4．2．4 抽条加固部分置换率优化

取不同的置换率进行计算分析，各置换率对应的坑外地表沉降及墙体最大位移见图15。

由图可知，虽然在曲线（坑外最大沉降）拐点位置出现了起伏的形态，但曲线斜率还是有一个比较明显的变化，因此可以据此认为置换率大约在0．2～0．3之间比较经济，原设计的置换率为0．27，是比较合理的。从控制墙体位移的角度看，最优置换率应控制在0．5左右。综合而言，最优置换率在0．3～0．5之间。

4．2．5 加固优化方案比选

综合4．2．1节至4．2．4节的结果，变电站基坑加固方案的参数优化如表3所示，加固深度在两个指标的控制下，最优解分别为0．9 H与1．1 H，若为了保证加固的效果，则取较大的值为最优值，若以经济性为主要考量，则取较小值。加固厚度没有明确的最优解，因此沿用原设计。6 m的裙边加固与置换率为0．3以上的抽条加固效果差不多，但考虑到裙边加固可以起到暗圈梁的作用，因此将原设计6 m的宽度折减一半予以保留。

图15　最大坑外沉降、墙体位移与抽条加固置换率关系Fig．15 Relationship between the largest settlement of ground outside the excavation／displacement of the wall and the replacement ratio

表3　基坑加固方案参数优化Table 3 Optim ization parameters of strengthening

优化方案与原方案的效果对比如表4所示，方案1相比原方案坑外最大沉降减少了4．5%，最大墙体位移减少了12．6%，但加固面积增加了7．6%，且加固深度增加了3．4 m之多。相比原方案，方案2坑外最大沉降减少了0．3%，墙体最大位移减少了4．5%，其加固面积减少了22%之多，且加固深度减少0．4 m。综合来看，优化方案2更具性价比，建议采用优化方案2。

表4　基坑加固方案对比Table 4 Comparison of strengthening schemes

5 结 论

本文采用连续介质模型，通过数值模拟，并结合已建基坑工程类比的方法对上海地区某220 kV典型变电站基坑的插入深度、坑内土体加固方案进行优化设计，得出以下结论：

（1）该地下变电站基坑的最优插入比为0．75～0．8，相比原设计节约了0．95～2．85 m的墙体长度。

（2）对坑内土体加固深度的优化，从控制坑外地表沉降角度看，最优加固深度为0．9H，从控制墙体位移的角度看，最优加固深度为1．1H。综合比较，最优加固深度为（0．95～1．1）H之间。

（3）在原设计抽条加固置换率不降低的条件下，可以将裙边加固完全改为抽条加固。

（4）对抽条加固置换率的优化，从控制坑外地表沉降角度看，置换率宜在0．2～0．3之间，从控制墙体位移的角度看，最优置换率宜取0．5。综合而已，最优值范围为0．3～0．5之间。

（5）不存在最经济加固厚度，需要控制多少位移，就应增加等比例的厚度。

（6）基坑坑内被动区土体加固可采用如下方案：加固深度17．1 m，加固厚度11 m，加固宽度3 m，抽条加固置换率0．3。

参考文献

［1］ 陈仲颐，叶书麟．基础工程学［M］．北京：中国建筑工业出版社，1990．Cheng Zhongyi，Ye Shulin．Foundation engineering ［M］．Beijing：Chinese Construction Industry，1990．（in Chinese）

［2］ 刘建航，侯学渊．基坑工程手册［M］．北京：中国建筑工业出版社，1997．Liu Jianhang，Hou Xueyuan．Excavation engineering handbook［M］．Beijing：Chinese Construction Indus-try，1997．（in Chinese）

［3］ 北京金土木软件技术有限公司．PLAXIS岩土工程软件使用指南［M］．北京：人民交通出版社，2010．Beijing Golden Civil Software Technology Co．，Ltd．PLAXIS geotechnical engineering software user guide ［M］．Beijing：China Communications Press，2010．（in Chinese）

［4］ 上海城乡建设和交通委员会．DG／TJ 08－61－2010基坑工程技术规范［S］．2010．Shangahai Orban-Rural Construction and Traffic Manggement Committee．DG／TJ 08－61－2010 Tech-nical code for excavation engineering［S］．2010．（in Chinese）

［5］ 徐中华．上海地区支护结构域主体地下结构相结合的深基坑变形形状研究［D］．上海：上海交通大学，2007．Xu Zhonghua．Deformation behavior of deep excava-tions supported by permanent structure in Shanghai soft deposit［D］．Shanghai：Shanghai Jiao tong Univer-sity，2007．（in Chinese）

基金项目：国家电网公司科技项目“地下变电站优化设计技术研究”（5150011044）联系作者，Email：329yangliu＠tongji．edu．cn

收稿日期：2014－08－21