船用飞轮电池永磁同步电机的灵敏度分析

郑海娇，Nicolas Bernard, 谢　卫

(1. 上海海事大学 电气自动化系，上海　201306； 2. Laboratory IREENA, Saint Nazaire, France)

船用飞轮电池永磁同步电机的灵敏度分析

郑海娇1，Nicolas Bernard2, 谢卫1

(1. 上海海事大学 电气自动化系，上海201306； 2. Laboratory IREENA, Saint Nazaire, France)

摘要：飞轮电池用于船舶中，因其具有充电快、放电完全的特点，非常适用于混合能量推动系统。选用永磁同步电机作为飞轮电机，首先对其进行基本电磁关系建模分析，并考虑约束条件。分析涡流损耗系数、磁滞损耗系数、附加损耗系数、外绕组半径与外定子半径比，内定子半径与外定子半径比对电机体积的影响灵敏度。结果表明，涡流损耗系数和附加损耗系数对电机体积的影响最大，电机定子半径比的影响较小，为电机的建模、设计、计算和制造提供了重要依据。

关键词：灵敏度分析；永磁同步电机；飞轮电池；船用

0引言

飞轮电池以其储能密度高、电能容易测量、体积小、充电时间短、使用寿命长、无任何废气废料等优点而被国际上认为是目前最有影响力的储能技术之一，具有广阔的发展前景。本文将飞轮电池用于船舶混合动力推动系统，并采用永磁同步电机作为飞轮电池中的能量转换装置。永磁同步电机因具有高功率密度和高转矩惯量比，成本低、结构简单、恒功率调速范围宽等特点，非常适合作为飞轮电池中的双向电机，并实现高效率、低损耗的能量转换。

本文针对船用飞轮电池中的永磁同步电机进行数学建模，在考虑饱和约束和热约束情况下，对涡流损耗系数、磁滞损耗系数、附加损耗系数以及定子半径比等重要损耗和结构参数对电机体积的影响灵敏度进行分析，为高效率、低能耗的电机设计和优化提供参考。

1永磁电机基本电磁关系

为简化问题首先做出以下假设:

1) 忽略所有的邻近边缘效应和泄漏电流的影响。

2) 电机在线性的磁场条件下运行，磁通密度不会超过饱和。

3) 电机的钢性部件假定为无限渗透的，并且只考虑磁场的基波。

4) 转子部分仅考虑气隙磁通密度的最优化。

本文考虑一个表贴式的永磁同步电机，电机模型如图1所示。

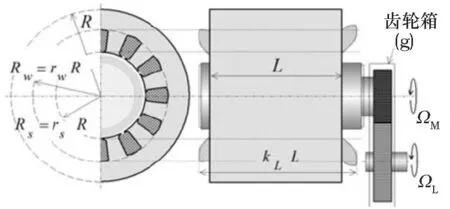
图1　永磁同步电机模型

其中左边为电机横截面示意图，R为外转子半径，RS为内转子半径，Rw为外绕组半径。电机有效长度为L，kL为考虑定子绕组端部影响的系数，本文中为kL=1.2，电机将链接一个齿轮箱g，其中ΩM为电机的机械角速度，ΩL为负载机械角速度。电机的电磁功率的表达式如下[1-3]:

(1)

上式中，Pem为电机的电磁功率，Bfm为磁通密度，Fs为定子磁动势，p为电机极对数。Rs为定子绕组阻抗，在考虑电机每槽导体为2ns，磁场成正弦分布，并且只考虑一次谐波的条件下，定义ρc为定子绕组电阻率，Sc为导线截面积，则定子绕组阻抗可以表示为:

(2)

为了减少电机的铜损耗，引入填充因子，它是通过有效导体的横截面积和电晕面积的比值来计算的，总面积则由定子内半径Rs以及绕组外半径Rw来定义的，如图2所示。此外，电机齿槽的填充系数为0.4，槽开口于齿开口率的比值为kt=0.5，从而填充因子为kf=0.2。这样电机的铜损耗表达为[4]:

(3)

图2　电机定转子模型

永磁同步电机的铁心损耗主要取决于电机的额定转速以及电机的极对数。此外，在电机制造的过程，永磁材料的磁异常以及冶金都会产生额外的铁心损耗，这些损耗可以通过实验测试获得。这里，电机的铁损耗表达式如下[4]：

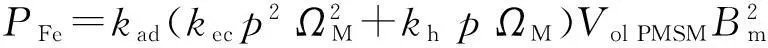
(4)

上式中Vol PMSM为永磁电机体积，Bm为电机磁通密度峰值，kec和kh分别代表涡流损耗和磁滞损耗的参考系数，kad是附加损耗系数，可以通过实验测试得到具体参数。为了获得附加损耗系数，可以令鼠笼式异步电机运行于不同的恒定电压/频率值数值下进行测量。本文中选定附加损耗系数为kad=3。

考虑任意的占空比，假设一个周期为T，在忽略风阻损耗条件下，电机的平均损耗表示为：

(5)

定义转矩随时间变化的函数为Temt=αBfmFs，电机磁动势可以写为：

(6)

其中，

(7)

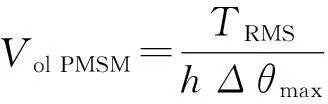
(8)

上式中，h为电机热传递系数，Δθmax为电机表面最高变化温度，取h=10 W/m2K，Δθmax=100℃。

2永磁电机约束分析

2.1饱和约束

电机磁通密度值是电机建模的重要参数，要避免电机定子和转子中的磁通密度超过饱和值而产生负面影响。磁通密度会直接影响电机的铁损耗，在电机高速运转时，电机的铁心损耗较为显著，可以通过减小永磁铁体积及电机磁动势来减小磁通密度，从而避免饱和效应。

将饱和约束定义为：Bym和Btm≤Bsat

其中Bym和Btm分别是电机齿和轭中的磁通密度，Bsat是饱和磁通密度，取Bsat=1.7T。

2.2热约束

永磁同步电机的建模分析中，热约束的分析是必不可少的，它不仅影响电机的磁场性能，同时也影响电机的电气性能。为了避免永磁体退磁、绝缘材料的劣化以及温度过高对机器造成的损害，热约束必须加以考虑。

仅考虑由电机绕组中的铜损耗和铁损耗所产生的热量，热约束则仅限于电机外表面的温度提升，且假设热量通过对流进行散热。假定电机外表面的最高温度为Δθmax=100℃，环境温度为常数θambient=20℃，电机表面温度在一个周期内的变化为[5]：

(9)

其中Plosses为电机总能量损耗，h为电机热传递系数，且h=10 W/m2K,Sth=2πR(R+L) 为电机的外表面积。

3永磁电机灵敏度分析

电机的结构设计和优化中，通常有许多参数可以进行调整，为了建立更准确的数学模型和设计方案，分析重要参数对于电机体积结构变化的灵敏度是非常必要的。灵敏度分析是电机设计优化的基础，通过灵敏度的分析，可以有效避免电机结构修改的盲目性，从而提高设计效率、减少设计成本[5]。本文中的灵敏度分析包括以下五个步骤：

1) 目标函数的选定

本文主要考虑的目标函数为式(8)所示的永磁同步电机的体积。

2) 变量及其变化范围的选定

在已建立的电机模型上，保持其他参数不变，只改变某一参数来分析该参数对电机结构的影响。本文中选取外绕组半径与外定子半径比值、内定子半径与外定子半径比值、附加损耗系数、涡流损耗系数以及磁滞损耗系数五种体积结构因素作为设计变量，进行灵敏度分析，如表1所示。

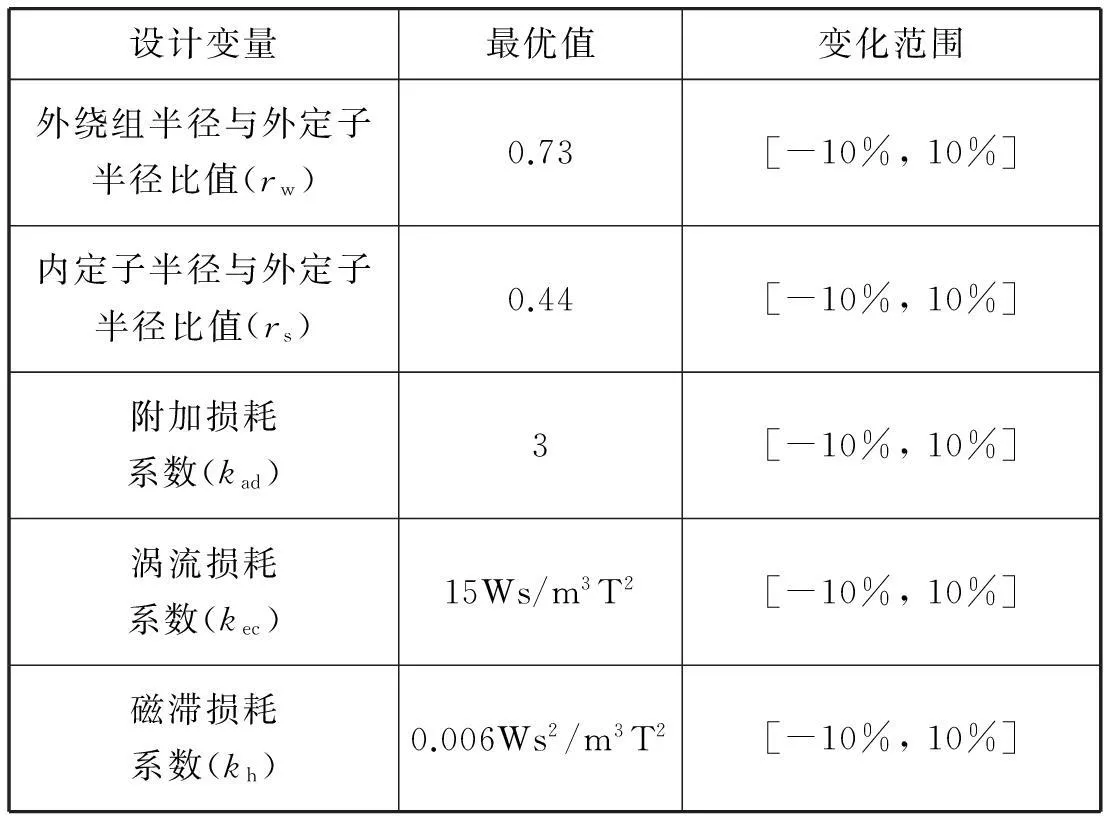
表1　设计变量数值及范围

3) 计算结果

定义相对误差为：

(10)

Xy分别代表rw,rs,kad,kec以及kh

为了得到更加清晰表明各项参数对于电机体积的影响灵敏度，这里定义功率体积比值为：

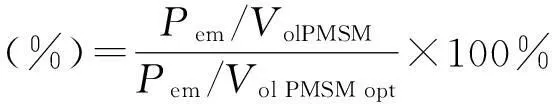
(11)

Vol PMSM opt为各项设计变量为最优值时的永磁电机体积。在不同转速下，各设计变量对于电机功率体积比的灵敏度计算结果如图3-7所示：

图3　外绕组半径与外定子半径比值分析

图4　内定子半径与外定子半径比值分析

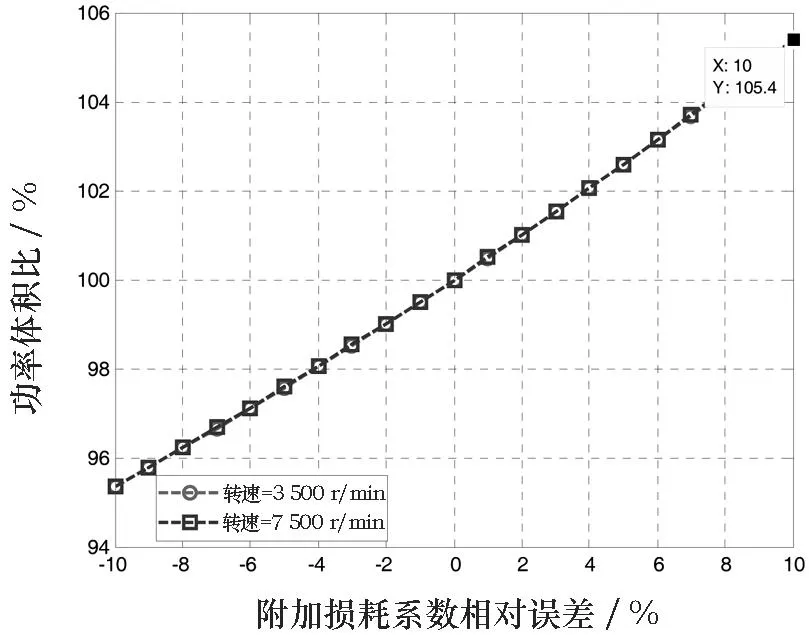
图5　附加损耗系数分析

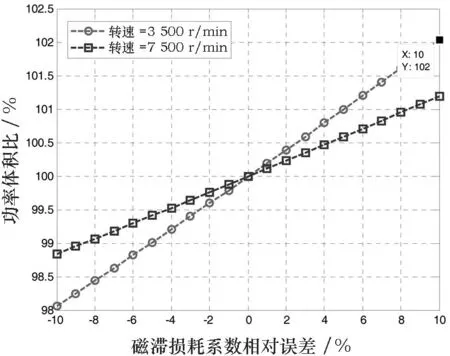
图7　磁滞损耗系数分析

计算结果表示，外绕组半径与外定子半径、内定子半径与外定子半径以及附加损耗系数对功率体积比的影响灵敏度与电机转速无关，而磁滞损耗系数与涡流损耗系数的影响灵敏度与转速密切相关。随着转速的升高，电机的功率体积比对涡流损耗的灵敏度也提高，对磁滞损耗的灵敏度则降低。对于电机的功率体积比，附加损耗系数和涡流损耗系数的影响灵敏度较大，外绕组半径与外定子半径比值和磁滞损耗的影响灵敏度较小，内定子半径与外定子半径比值的影响最小。

定义电机功率与体积的比为：

(12)

磁滞损耗系数与涡流损耗系数对电机结构影响的灵敏度与电机转速相关，在转速为自变量时计算结果如下：

图8　涡流损耗系数影响的灵敏度

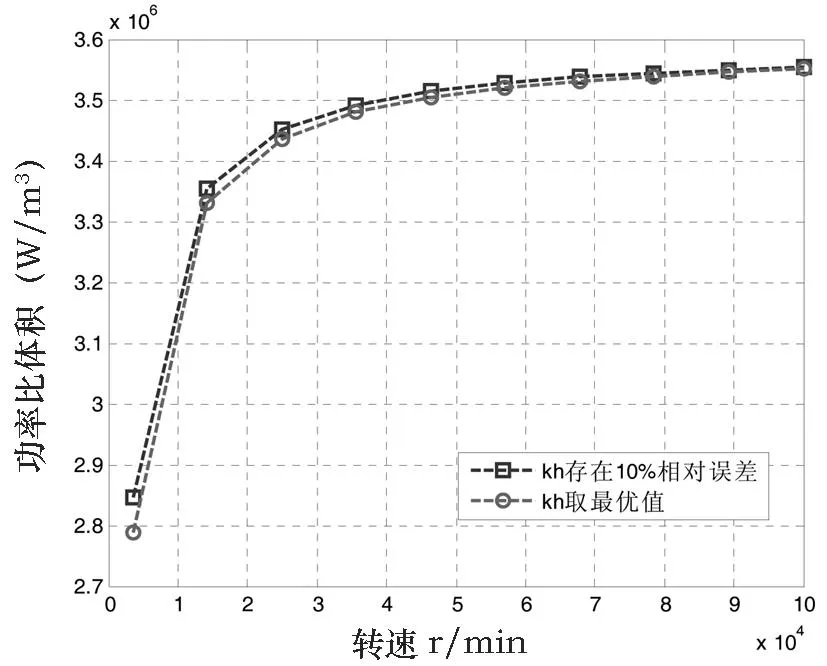
图9　磁滞损耗系数影响的灵敏度

图8和图9可见，电机功率比体积的值在转速低于大约15 000 r/min时随着转速的提升将急速上升，转速的继续升高，曲线上升趋势将逐渐降低最终趋于平行。如图8所示，当转速低于14 220 r/min时，kec存在10%相对误差及取最优值时电机功率比体积的差值相对较小，但当转速高于14 22r/min时，两者之间的差距会明显增大并随着转速的继续升高基本保持不变。如图9所示，两条曲线基本保持重合，即磁滞损耗系数对于电机结构影响的灵敏度较低，在实际应用中需要特别注意。

4结语

本文在建立船用飞轮电池永磁同步电机数学模型的基础上，计算了各项损耗及结构参数对电机体积结构的影响并进行了灵敏度分析。研究表明，附加损耗系数和涡流损耗系数影响的灵敏度较大，而外绕组半径与外定子半径比、内定子半径与外定子半径以及磁滞损耗的影响灵敏度相对较低，为电机的设计优化提供了重要参考。

参考文献

[1] R.Missoum, N. Bernard, E.H. Zaïm, and J. Bonnefous, Optimization of high speed surface mounted permanent magnet synchronous machines, in Proc. Int. Aegean Conf. Elect. Mach. Power Electron., Bodrum, Turkey, Sep. 10-12,2007, pp. 446-451.

[2] 左曙光，马琮淦，何融，孙庆，孟姝，车用永磁同步电机径向力波灵敏度分析和优化，振动、测试与诊断，2013,33(3):357-363.

[3] N. Bianchi, S. Bolognani, and P. Frare, Design criteria for high-efficiency SPM synchronous motors, IEEE Trans. Energy Conversion, vol. 21, no. 2, pp. 396-403, Jun. 2006.

[4] N. Bernard, F. Martin, E.H. Zaïm, Design methodology of a permanent magnet synchronous machine for a screwdriver application, IEEE Trans. on Energy Conversion, vol.27,no.3, pp.624-633, 2012.

[5] 何吕昌，左曙光，马琮淦，文岐华，魏欢，相龙洋，永磁电机定子参数化建模及结构灵敏度分析，微电机，2012,45(9):13-17.