电网连锁故障中的受扰支路及其关联节点分析

邓慧琼，李培强，郑荣进

（福建工程学院信息科学与工程学院，福建福州350118）

电网连锁故障中的受扰支路及其关联节点分析

邓慧琼，李培强，郑荣进

（福建工程学院信息科学与工程学院，福建福州350118）

针对电网的连锁跳闸现象，对受初始故障波及的连锁受扰支路及其与电网节点的关联关系进行分析，并提出一种筛选初始故障、连锁受扰支路以及对连锁受扰支路的关联节点进行划分的算法。首先根据连锁跳闸现象中连锁受扰支路的连锁跳闸表现，以及继电保护的动作行为，给出一种评价连锁受扰支路受扰严重性的表达形式，在此基础上给出根据严重性对连锁受扰进行筛选的原则，然后分析初始故障切除后剩余系统支路的电流和节点注入功率之间关系，进而在综合连锁受扰支路的严重性及其与节点关联作用的基础上，形成筛选初始故障支路及其相应的严重连锁受扰支路以及对严重连锁受扰支路的关联节点进行划分的算法，可为电网分析连锁跳闸现象以及阻断连锁跳闸提供思路和借鉴，算例分析表明该算法的合理性。

电力系统；大停电；连锁故障；连锁跳闸；潮流转移；关联作用

电网的连锁故障问题一直是近些年来比较受到关注的一个热点问题。广大研究工作者从大规模连锁故障发生的自组织临界性［1］，电网拓扑的小世界网络特性［2］，电网连锁故障产生的风险［3］，电网连锁故障引起的脆弱性［4］，连锁故障发展的事故链［5］等多种角度对电网连锁故障现象及相关问题进行了研究，取得了众多的研究成果。

电网连锁故障通常从一个简单的故障开始，其通常的表现是：一条线路故障且被切除后（这是第一级故障），然后因连锁受扰作用使得电网剩余的支路中有部分支路被继电保护或自动装置切除（这是第二级故障），然后进一步引起新的线路或元件跳闸（第三级），依次类推，期间，可能伴随着复杂的动态过程。一般而言，随着连锁故障的发展，动态过程会越来越复杂。

从防御连锁故障的角度来看，显然越早阻断连锁故障的发展越是有利的，从紧急控制的角度来看，显然在第一级故障发生后，就应该采取措施。实际上，在很多的电网连锁故障中，第一级故障发生后往往并没有复杂的动态过程，而只是潮流发生了重新分配，使得电网中其余的支路发生过载进而被继电保护切除。虽然在这一阶段实际的电网中一般有静态安全分析和控制的措施，但实际电网复杂多变，静态安全分析并不一定能够捕捉所有可能引发连锁故障的初始故障，历史上发生的不少大停电事故往往就是因为这种情况的出现而导致的。所以将这一阶段的连锁跳闸现象作为一种特殊的问题加以研究还是很有必要的，对此近年来出现的输电断面保护［6］提供了很好的思路和借鉴，考虑到初始故障切除后电网潮流一般转向与初始故障线路处于相同输电断面的线路上，所以其思路是通过适当的算法快速识别与初始故障线路位于相同输电断面的线路，进而采取措施以避免连锁跳闸事故的发生。

由于连锁跳闸现象与连锁受扰支路在潮流重新分配后的电气量及其所配置的后备保护的动作行为密切相关，因此本文结合这些因素给出了一种评价连锁受扰支路的表达形式，并根据其连锁受扰的严重性给出了筛选连锁受扰支路的原则。同时，考虑电网潮流的重新分配主要决定于节点的注入功率，而且阻断连锁跳闸的主要手段是削减节点的注入功率，本文分析了初始故障支路切除后电网其余支路的电流和节点注入功率之间的关系，然后在综合前面分析的基础上提出了一种筛选初始故障支路、连锁受扰支路并对其关联节点进行划分的算法，最后在IEEE39系统上通过算例给出进一步的分析和验证。

1 连锁受扰支路的严重性评价

设电网某时刻支路Lk发生初始故障，当支路Lk切除且电网的潮流重新分布后，对于剩余系统中的任一支路Li，根据其后备保护的配置情况，可定义如下的变量来衡量该支路是否发生连锁跳闸：

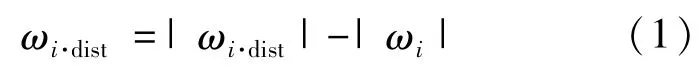
其中，ωi·dist是衡量ωi·lim和ωi之间电气距离的量，其所表示的含义是：当ωi·dist≤0时，支路Li由后备保护予以切除，而当ωi·dist＞0时，支路Li不会被后备保护切除；而ωi·lim和ωi则是由具体的后备保护配置及其动作方程决定的量，可根据具体情况来确定。例如，若保护为电流保护，则ωi·lim为保护的电流定值，而为ωi支路Li的电流；若保护为方向圆特性的距离保护，则ωi·lim可取为Zset／2，而ωi可取为Zm-Zset／2，其中，Zset为距离保护定值，而Zm为测量阻抗。由式（1）可见，在不考虑保护动作的不确定性以及其他闭锁条件的情况下，从连锁跳闸的角度来看，ωi·dist的取值实质上也反映了支路Li在初始故障切除后因连锁作用而受到扰动的严重程度。可利用式（2）来进一步给出连锁受扰支路的严重性。

其中的ε为用于判断的门槛值，可以为很小的正数或负数，可根据经验或实际的需求给出，一旦给定ε，则式（2）实际上也就给出了筛选严重连锁受扰支路的原则，即对任一支路只要满足式（2）即可视为严重连锁受扰支路。下面主要针对电流保护的形式展开进一步的讨论。

2 初始故障切除后节点-支路间关联关系

当电网中的支路Lk因发生初始故障断开后，在近似地只考虑有功功率的情况下，电网剩余系统中的某一支路Li的传输功率将由Pi（0）变为Pi，即：

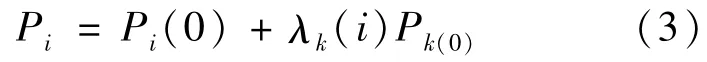
其中，Pk（0）为支路Lk故障前所传输的功率，λk（i）是一个由网络结构和支路电抗参数共同决定的量，反映的是Lk断开后，其原来所传输的功率分配在支路Li中的份额。设电网共有l条支路，n个节点，如果连同支路Lk一并考虑在内，将电网的每一条支路的传输功率按式（3）组合起来，可形成如式（4）所示缩写的矩阵形式：

PL＝PL（0）＋Pk（0）λ（4）

式（4）中PL为支路Lk开断后的支路功率向量，共包含l个元素；PL（0）为支路Lk开断前的支路功率向量；λ是各支路的λk（i）组成的向量。

根据直流潮流法可知，式（4）中的PL（0）与支路Lk开断前电网各节点的电压相角向量θ0具有式（5）所示的关系［9］：

PL（0）＝Sθ0（5）

其中，θ0中的参考节点的电压相角取为0；S为支路-节点关联矩阵，其中的每个元素记为sij（i＝1，2，…，l；j＝1，2，…，n），如果支路Li和节点j不相连，则sij＝0；如果支路Li的功率从节点j流出，则sij＝1／x；如果支路Li的功率注入节点j，则sij＝-1／x。这里，x为支路Li的电抗。

设θ0中除去参考节点以外的其余节点组成的向量为θ0′，由直流潮流法可知，θ0′和节点注入功率向量之间的关系为［7］：

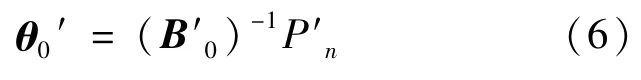
式（6）中B0′为支路开断前对应于不包含参考节点的n-1阶节点电纳矩阵；Pn′为不包含参考节点的节点功率注入向量。对矩阵（B0′）-1进行扩展［8］，也即给（B0′）-1增加一行一列，该行和列的各元素的值都取为“0”，其行号和列号都对应于参考节点的编号，其余各行各列的编号分别和其余各节点的编号对应，并将扩展后的矩阵记为B0。进一步取Ik表示l×l阶单位阵的第k行，则可进一步推得［8］：

PL＝［SB0＋λIkSB0］Pn＝RpPn（7）

其中，Pn为电网中包括参考节点在内的节点注入功率向量。Rp为由SB0＋λIkSB0构成的系数矩阵，其中的每个元素记为rij（i＝1，2，…，l；j＝1，2，…，n），其中的λ的计算可参见文献［9］。

根据直流潮流法的假设条件及支路电流和传输有功之间的关系［8］，可知支路Lk开断后，其余各支路的电流为：

I＝RpPn（8）

这样，式（8）就给出了支路Lk开断后，电网节点注入功率和各支路电流之间的关系。

由式（8）可见，支路Lk开断后，任一支路Li的电流可表示为：

式（9）右侧的任一元素rijPj（j＝1，2，…，n）代表了节点j对支路Li的实际贡献，而rij则代表了节点j对支路Li的灵敏作用。

3 支路的筛选及关联节点的划分算法

由前面的分析可见，对于连锁跳闸事件，在进行预想事故分析时首先应该按照连锁跳闸的实际情形分析连锁受扰支路。其次，初始故障支路断开后，由于受扰支路的电流主要决定于节点的注入功率，而且往往与部分节点之间的关联关系比较大，找出对连锁受扰支路起关键作用的节点，可为分析连锁跳闸以及制定消除连锁跳闸的预案提供依据。为此，本文主要提出以下的算法对初始故障支路和连锁受扰支路进行筛选，并对关键节点进行划分，在算法中，由于考虑到连锁受扰支路首先要涉及到初始故障支路，所以为了给出完整的算法，在重点分析连锁受扰支路的同时，也将初始故障支路的选择一并考虑进来，算法的主要思路如下。

1）对选定的预想初始故障，利用式（8）进行计算，并根据计算的结果依据式（2）判断所分析的预想初始故障是否存在满足式（2）的情况，如果存在，则将所分析的预想初始故障选入初始故障集Sfailure（1）中，从而初步筛选出比较严重的初始故障。由于式（8）是采用直流法进行分析，其误差一般能达到10%［10］，所以在计算式（2）中的ωi·dist时，按式（10）进行计算：

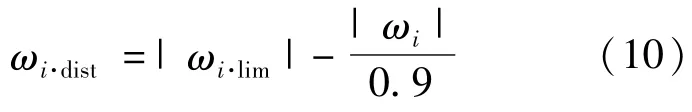
其中的ω均按电流来考虑。

2）根据第一步选到的初始故障集Sfailure（1），利用精细潮流计算进行进一步的分析，并依据式（2）判断所分析的预想初始故障是否存在满足式（2）的情况，如果存在，则将所分析的预想初始故障选入初始故障集Sfailure（2）中，同时，对选入Sfailure（2）中的任一初始故障支路，确定包含严重连锁受扰支路的集合Ssub。Ssub可表示为：

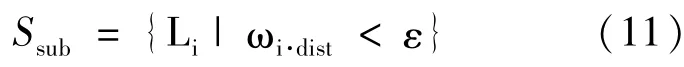
其中的ωi·dist也同样按电流来考虑。

3）针对Sfailure（2）中任一初始故障支路所对应的Ssub中的每一条支路Li根据式（8），提取Rp矩阵中的相应元素rij（j＝1，2，…，n），以及rijPj（j＝1，2，…，n），然后采用聚类分析方法进行划分。分析时以rij和rijPj作为特征输入量，这样做既可以考虑到节点对支路Li的灵敏作用，同时也可以考虑到各节点对支路Li的实际贡献作用。

整个算法的流程如图1所示。算法中第二步主要通过精细潮流计算进行分析，之所以采用这样的方式，主要是考虑到采用精细计算更适合对后备保护的动作进行分析。

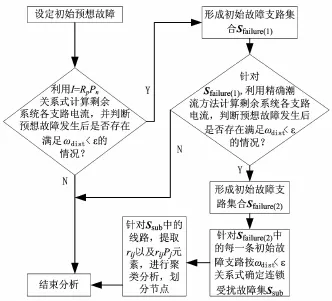
图1 算法流程图Fig．1 Flow chart of the algorithm for selecting disturbed branches and classifying correlational nodes

对于算法中所采用的聚类分析方法，本文将采用FCM算法。在分析中，令输入的第k个样本yk＝（rik，rijPj）（k＝1，2，…，n）。设C为样本的分类数目，而m1，m2，…，mC为每个聚类的中心，μh（yk）为第k个样本对于第h类的隶属度函数。用隶属度函数定义的N个样本的聚类损失函数可写成［11］：

其中，b＞1是一个可以控制聚类结果的模糊程度的常数，其取值通常在2左右［12］。式（12）中各个聚类的隶属度应满足其和为1的条件，即：

在满足式（13）的条件下，式（12）所示的目标函数为最小的必要条件是：

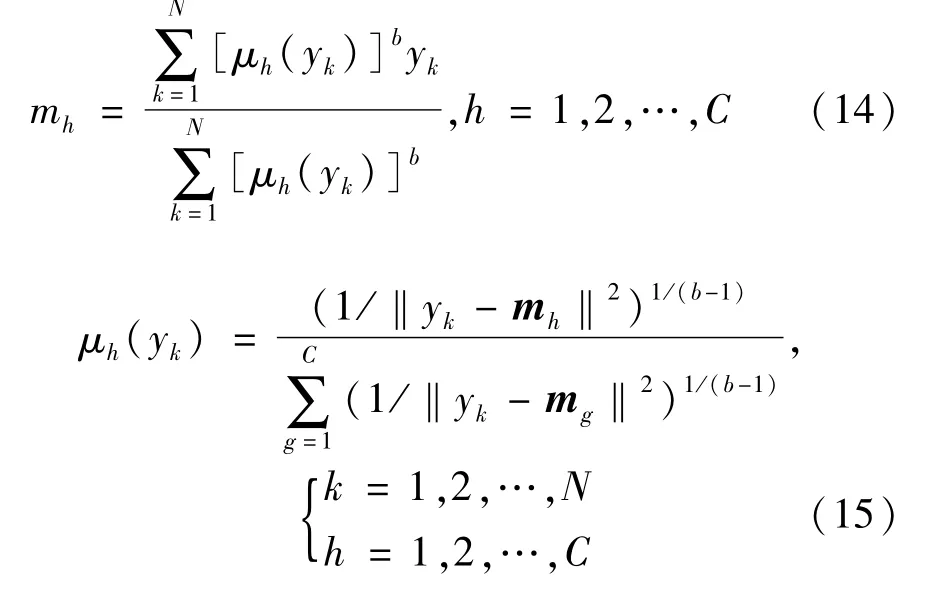
得到了上述的基本条件之后，在对严重连锁受扰支路的关联节点进行划分时可以采用迭代的方法进一步去确定各个聚类中心m和隶属矩阵U［11］：

为了确定最佳分类数，本文采用划分系数来确定。其中划分系数的定义为［13］：

采用划分系数对聚类结果进行有效性判决的标准是：划分系数最小的分类数即为最佳分类数［13］。同时，由于样本数据的数目一般是有限的，分类数按照从2逐步增加的方式，最终再根据划分系数确定最佳分类数。

4 算例分析

以IEEE 39节点系统为例对所提算法给出进一步的说明。算例系统的接线图如图2所示。

图2 算例系统接线图Fig．2 Connection diagram of calculation exam p le system

按照前面给出的算法步骤和给定的算例系统，编制了MATLAB计算程序，按照前述算法进行分析，下面给出详细的算例说明，在分析中系统中各元件的参数以标幺值表示，其中基准容量取为100MVA。

1）设定预想初始故障为算例系统中的所有线路，然后针对每一初始故障，首先按式（8）计算剩余系统中的各支路的电流，然后按式（10）计算各支路的ωi·dist值，再按式（2）判断每一支路是否满足式（2）的条件，其中，ε取为0．01，对于后备保护的电流定值，假定其为基态潮流状态下的电流的2．6倍，这个值主要是为了算例演示，是一个假定的数据。在随后的分析中，针对每一初始故障，只要剩余系统中的任一支路满足式（2）的条件，就将该初始故障线路送入Sfailure（1）集合中。经过分析，共有4条线路进入了Sfailure（1）集，分别为L1-2，L2-3，L21-22，L26-27，其中L1-2表示节点1、2之间的线路，其余类推。

2）针对Sfailure（1）集，利用精细潮流法进行计算，采用基于牛顿法的潮流计算方法进行了详细分析，结果表明上述的4条线路的每一条作为初始故障支路时也满足（2）的条件，所以这4条线路都被选入集合Sfailure（2）当中。在这一步的分析中，对于每一条初始故障线路，一旦判定其连锁受扰支路满足式（2），即对其余剩下的连锁受扰支路进行详细分析，并分析其是否满足式（2）的条件，进而记录详细的结果，给出Ssub集合。

作为例子，这里给出线路L21-22发生初始故障后的连锁受扰支路，分别为：L16-24，L17-27，L22-23，L23-24，一共有4条支路。

3）针对每一个Ssub集合的连锁受扰支路，根据式（8）提取Rp矩阵中相应的对应的rij和rijPj（j＝1，2，…，n）数据，图3给出了连锁受扰支路L16-24，L17-27对应的数据，图4给出了连锁受扰支路L22-23，L23-24对应的数据。其中的横轴代表节点的序号。

按照前述算法，接下来针对每一条连锁受扰支路，根据提取出来的rij和rijPj数据并以其为特征量进行聚类分析，进而实现对所有的节点进行划分，以评估不同的节点对支路L16-24的作用。

图3 支路L16-24，L17-27的rij和rijPj数据Fig．3 The data of variable rijand rijPjcorresponding to branch L16-24and L17-27

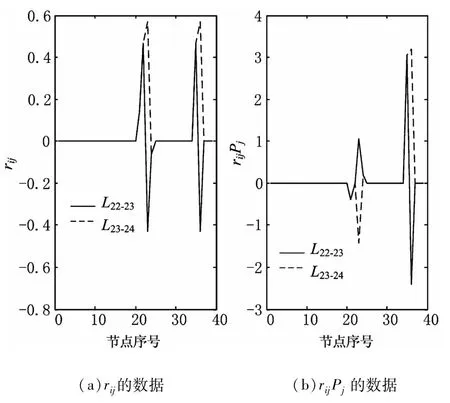
图4 支路L22-23，L23-24的rij和rijPj数据Fig．4 The data of variable rijand rijPjcorresponding to branch L22-23and L23-24

以连锁受扰支路L16-24为例，经过聚类分析后，一共分为6类，第一类相关的节点共有33个，其聚类中心为［0，0］，其中左边的“0”代表的是rij数据，右边的“0”代表的是rijPj数据，后面其余几类的数据也按这种顺序列出，第一类的数据表明其对应的节点对支路L16-24的灵敏作用和实际贡献都不大。第二类相关的节点只有一个，其聚类中心为［-0．468 8，0］，这个节点是节点22，其结果表明，虽然节点22对支路L16-24有一定的灵敏作用，但是实际贡献为零，从网络的接线图来看，由于节点22既非发电节点亦非负荷节点，因而对支路L16-24的实际贡献为零是符合实际的。第三类的聚类中心为［-0．519 3，-3．118 8］，相应的节点共有两个，分别是节点35和节点36，这两个节点都是发电节点，无论是灵敏作用还是实际贡献对支路L16-24的影响都比较大，从网络的接线图来看，支路L21-22也是节点35、36上的发电功率的外送通道，当支路L21-22断开后，节点35、36上发电功率只能通过支路L16-24外送，对支路L16-24的影响自然比较大。第四类的聚类中心为［-0．937 9，2．894 5］，对应的节点为节点24，其对支路L16-24的灵敏作用和实际贡献也都比较大。第五类的聚类中心为［-0．569 8，1．410 1］，对应的节点为23，其对支路L16-24的灵敏作用和实际贡献也都比较大，但要次于节点24。第六类聚类中心［-0．142 0，0．389 1］，对应的节点为节点21，其对支路L16-24也有一定的影响，但要比节点23和节点24的要小很多。结合图2和图3可见，对支路L16-24作用比较大的节点主要是节点23、24以及节点35、36，节点21也有一定的影响，实际上这些节点主要是分布在支路L16-24右侧的一些发电节点和负荷节点，在支路L21-22断开后，由于功率平衡的需要，这些节点对支路L16-24产生了较大的作用。如果支路L16-24发生了连锁跳闸，则系统解列为两部分，所以支路L21-22的运行情况要受到关注，而受到其连锁扰动的支路L16-24则更应受到关注，相应地，与其关联比较强的节点23、24、35、36的注入功率及功率的变化也应适时掌握，当出现紧急情况时，在允许的条件下，若对上述几个节点上的注入功率采取限制措施，由式（8）可见可取得比较快捷有效的结果。

通过上述算例可见，利用本文的算法可根据后备保护的实际动作情况，筛选出初始故障支路，并对受初始故障波及的严重连锁受扰支路进行筛选，同时，通过对严重连锁受扰支路所关联的节点进行划分，可对进一步采取措施或预防连锁跳闸提供帮助。

5 结论

电网的连锁跳闸现象与连锁受扰支路的继电保护的动作密切相关，本文结合继电保护的动作行为，根据连锁受扰支路的后备保护的动作方程给出了连锁受扰支路的评价，可较为真实地反映连锁跳闸行为，所给出的筛选初始故障及连锁受扰支路的算法较为接近连锁跳闸的实际情况。同时在初始故障切除后的初级阶段，连锁跳闸往往是因为电网潮流的重新分配引起的，而潮流的重新分配主要决定于节点的注入功率。研究连锁受扰支路的电气量与节点注入功率之间的关系，并对不同的节点按照其对连锁受扰支路的灵敏关系和实际作用进行分组划分，对于掌握在连锁跳闸中起关键作用的节点，以及在紧急情况下采取防御措施都是有利的。本文所提出的算法，通过算例演示表明是简洁有效的，可为进一步的研究提供借鉴。

［1］曹一家，张宇栋，林辉，等．基于同配性的电力系统自组织临界性识别［J］．电力自动化设备，2013，33（7）：6-11，18．

［2］郑阳，刘文颖，温志伟，等．基于小世界网络的电网连锁故障实时搜索系统［J］．电网技术，2010，34（7）：58-63．

［3］付蓉，蒋国平，王保云．计及系统连锁故障风险的电网预防控制［J］．电力系统保护与控制，2011，39（3）：12-17．

［4］李勇，刘俊勇，刘晓宇，等．基于潮流熵测度的连锁故障脆弱线路评估及其在四川主干电网中的应用［J］．电力自动化设备，2013，33（10）：40-46．

［5］王英英，罗毅，涂光瑜，等．采用图论的电网连锁故障模式搜索方法［J］．高电压技术，2010，36（2）：401-405．

［6］姚峰，张保会，周德才，等．输电断面有功安全性保护及其快速算法［J］．中国电机工程学报，2006，26（13）：31-36．

［7］吴际舜．电力系统静态安全分析［M］．上海：上海交通大学出版社，1985．

［8］徐刚．由潮流转移引起输电网脆弱性的综合评价方法研究［D］．石家庄：河北科技大学，2014．

［9］邓慧琼，李争，杨国福，等．电网连锁故障激发因素研究［J］．河北科技大学学报，2010，31（3）：222-226．

［10］邓慧琼，艾欣，赵亮．电网连锁故障分析方法评述［J］．现代电力，2007，23（6）：10-20．

［11］边肇祺，张学工．模式识别［M］．北京：清华大学出版社，2000．

［12］李洁，高新波，焦李成．一种基于修正划分模糊度的聚类有效性函数［J］．系统工程与电子技术，2005，27（4）：723-726．

［13］范九伦，吴成茂．划分系数和总变差相结合的聚类有效性函数［J］．电子学报，2001，29（11）：1561-1563．

（责任编辑：肖锡湘）

Analysis of disturbed branches and their related nodes in the cascading failures scenario in power network

Deng Huiqiong，Li Peiqiang，Zheng Rongjin
（College of Information Science and Engineering，Fujian University of Technology，Fuzhou 350118，China）

To dealwith cascade tripping in power network，the disturbed branches affected by the initial power cascading failure and the correlation between the disturbed branches and the nodes of power network were analysed．An algorithm for selecting the initial failures and the seriously disturbed branches and classifying the related nodeswas proposed．Firstly，an evaluation expression for evaluating the severity of the disturbed brancheswas presented，which was based on the performance of the cascade tripping of the disturbed branches and the operating action of the relay of disturbed branches．A principle of selecting the disturbed branches in relation to the severity of the disturbance was proposed．The correlation between the currentof the branches in the remaining system after removing the disturbed branches and the injection power of the nodes was analysed．The algorithm was proposed by combining the severity of the cascading disturbed branches and the correlational nodes．A computation example in IEEE39 system proves the rationality of the proposed algorithm．

power system；blackout；cascading failure；cascade tripping；power flow transfer；correlation

TM7

A

1672-4348（2015）03-0223-06

10．3969／j．issn．1672-4348．2015．03．004

2015-04-20

福建省自然科学基金项目（2015J01630）；福建省教育厅项目（JB13143）；福建工程学院科研项目（GYZ13104）

邓慧琼（1972-），男，山西大同人，副教授，博士，研究方向：电网连锁故障。