三自由度平动手控器重力补偿研究

刘世平，余昆，李世其，王博，宋樊

(华中科技大学 机械学院，湖北 武汉 430074)



三自由度平动手控器重力补偿研究

刘世平，余昆，李世其，王博，宋樊

(华中科技大学 机械学院，湖北 武汉 430074)

摘要：设计、加工三自由度平动手控器，通过静力学计算以及ADAMS仿真分析，求解出任意位置平衡手控器运动部件重力所需的电动机驱动力矩，并将计算结果应用于手控器的操作过程中。试验表明，重力补偿能有效地消除手控器运动部件重力对操作者的影响，减轻疲劳感，提高了机构的可操作性与操作效率。

关键词：手控器；重力补偿；静力学分析

0引言

人机交互式机器人作为最具实用价值的特种机器人已成为当前机器人学研究的前沿和热点。临场感技术是人机交互的核心[1]。在遥操作机器人中应用临场感技术，能极大地提高安全性和操作效率、改善机器人作业能力。遥操作技术中临场感主要体现在视觉、听觉、力觉、触觉等方面，手控器是一种用于虚拟现实技术中的力觉人机交互设备[2]，也可拓展为力触觉反馈设备。由于其具有位置输出的交互控制功能与力觉反馈功能，手控器成为近年来遥操作交互技术以及临场感技术中的重要研究课题。按照手控器组合机构的结构形式,可分为串联式,并联式和复合式[5]。并联机构由于具有结构刚度大、承载能力强、运动精度高、惯性小等特点，逐渐成为国际上研究的热点[6,7]。Delta机构[8]就是一种典型的并联机构。由于Delta机构的运动部件的质量不能忽略，而重力始终向下，有必要进行重力补偿以消除运动部件所受重力对操作者的影响。重力补偿的方法一般有三种：弹簧法，配重法，驱动法[9]。文中设计了基于Delta机构的三自由度平动手控器，并基于驱动法运用静力学计算以及ADAMS仿真对手控器进行重力补偿分析，消除手控器在操作过程中的重力影响，结果表明静力学计算结果与仿真结果接近，且能有效消除重力影响，提高手控器的操作性能。

1手控器结构及重力补偿问题描述

1.1　手控器结构及原理

三自由度平动手控器如图1、图2所示，主要结构为静平台、动平台以及三个对称分布的运动支链，运动支链由平行四边形机构与a2杆构成，传递人手的平移运动以及电动机的旋转运动。该手控器有x、y、z三个方向的平动自由度。手控器具有运动控制以及力反馈的功能，其工作原理为：一方面操作者移动把手，通过各支链的光电编码器检测出a2杆转动角度，反解出动平台参考点在x、y、z方向的平移距离，以此平动距离遥操作远端设备，如机械臂末端抓手；另一方面远端设备与环境发生力的作用(如机械手的抓握)，经传感器检测出之后反馈给操作端，电动机输出力学结算得到的力矩，经过运动支链的传递，给操作者以力感。

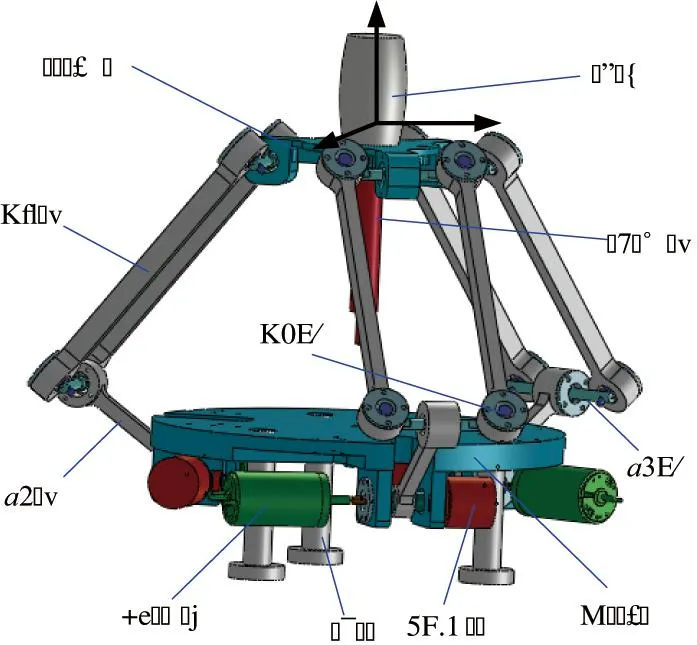
图1　手控器三维模型

图2　手控器机构

1.2　重力补偿问题描述

delta并联机构结构较为复杂，运动部件包含的零件较多，为了减轻运动部件的质量，在设计制造过程中尽可能地优化零件、使用密度较小的材料，但对加工完成的运动零部件加以精确称量得出其总和达到2350.751g。较大的自重导致操作者在操作过程中需克服较为明显的重力作用，长期操作极易形成疲劳感。经实验检测，在无重力补偿情况下操作手控器，运动支链位于一般位置时操作者需要承受12~20N的作用力，操作时间持续一分钟以上就会产生疲劳感；另一方面，手控器在进行力反馈时，无重力补偿时反馈力将和运动部件重力共同作用于人手，造成反馈力不真实，力反馈效果较差，力觉临场感无法实现。所以对手控器进行重力补偿、消除运动部件的重力影响是必要的。

重力补偿即为机构的静平衡问题[10]，采用驱动法对手控器的重力补偿问题进行研究。驱动法需要计算平衡重力所需力矩，然后驱动电动机来产生相等力矩值，以此来平衡机构重力[9]。图3为基于驱动法的重力补偿流程图。

图3　重力补偿流程图

图4　手控器静力学模型

2手控器重力补偿研究

2.1　基于静力学计算的重力补偿研究

delta机构属于杆支撑并联机构，静力学分析是对其进行其他力学分析的基础[11]。手控器在工作过程中处于低速非连续运动状态，所受的载荷主要包括人手作用力，电动机驱动力矩以及机构运动部件的自重。机构在合力作用下取得静力平衡。图4为手控器静力学模型。

对于运动支链中的平行四边形机构，忽略各部件的质量不均匀性，其质心始终位于平行四边形的中心。在建模计算时，通常将平行四边形机构和a2杆组件简化为质量集中于质心点的二力杆。

模型中AiBiCi(i=1,2,3)为运动支链，点O、P为静、动参考平面中心，θi(i=1,2,3)为各运动支链电动机转角，R为静平台半径，r为动平台半径，Δr=R-r为静动平台半径差。忽略杆长在制造中的误差，la为a2杆有效长度，lb为平行四边形机构等效杆件长度。

手控器静力学问题可以描述为：机构自重包括动平台部分的重力G1、平行四边形机构重力G2i(i=1,2,3)、a2杆重力G3i(i=1,2,3)，机构所受外力(人手作用于把手上的力)F=(Fx，Fy，Fz)，各电动机的输出平衡力矩力矩为M1，M2，M3，忽略关节摩擦力，在静力平衡条件下，求取各杆件作用力与反作用力。表1为手控器运动部件的重力表。

表1　手控器三运动支链各运动部件重力　N

操作过程中人手作用于机构上的力F不可知，且重力补偿的目标是在机构的任意运动位置求解出平衡机构运动部件重力所需的电动机输出力矩Mi(i=1,2,3)。在静力学的基础上取外力F=(0，0，0)，求解出电动机需输出的平衡力矩M1，M2，M3，并控制电动机输出相应力矩，消除机构运动部件的重力的影响。图5为手控器重力补偿模型。

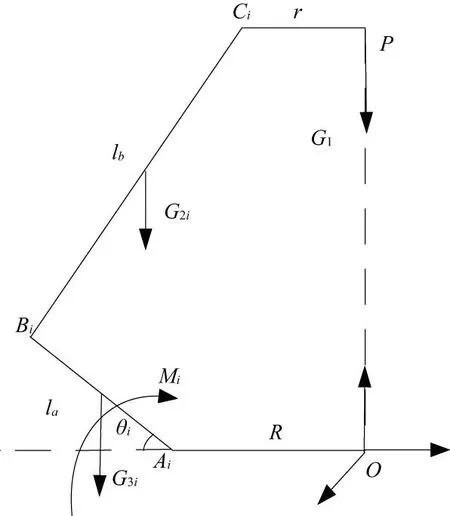
图5　手控器重力补偿模型

根据虚位移原理[12]，手控器在任意运动位置静力平衡的条件为：

M1δθ1+M2δθ2+M3δθ3+FTδX+δP=0

(1)

其中：δθ1,δθ2,δθ3为a2杆在驱动力矩作用下的虚转角位移；δX为机构质心处作用力下的虚位移向量。δX=(δx,δy,δz)T，P为机构的重力势能。以往的文献中，通常将并联机构各支链运动部件的质量当作相同来计算，不考虑实际情况中由于制造存在的误差，本次研究中按各实际质量进行计算，即：

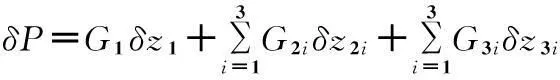
(2)

其中：δz2i、δz3i分别是第i(i=1,2,3)支链的平行四边形机构、a2杆沿z方向运动的虚位移量。

由于重力补偿情况下不考虑静力学中的主动力F，所以式(1)可以转化为运动部件重力与电动机平衡力矩所作的虚功相等：

M1δθ1+M2δθ2+M3δθ3+δP=0

(3)

由于虚位移的的任意性，令(δθ2,δθ3)为(0，0)，得到:

(4)

同理，分别令(δθ1,δθ3)、(δθ1、δθ2)为(0，0)，得到：

(5)

(6)

合并式(4)、式(5)、式(6)可得表达式(7)：

(7)

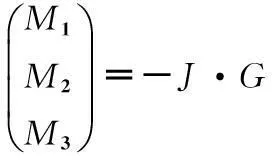
(8)

a) 求解雅克比矩阵J

在手控器的运动学分析中，得到手控器三方向平动距离x、y、z与电动机转角θi(i=1,2,3)的运动关系为：

x2+y2+z2-2xcosi(Δr+lacosθi)-2ysini(Δr+lacosθi)-

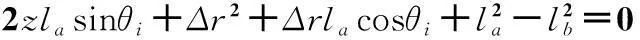
(9)

令:

F(x,y,z,θi)=x2+y2+z2-2xcosi(Δr+lacosθi)-2ysini

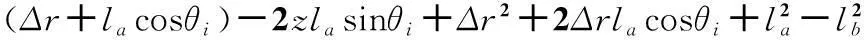
(10)

则:

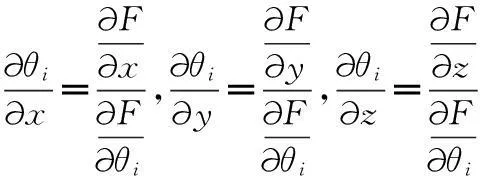
(11)

根据式(10)，可得:

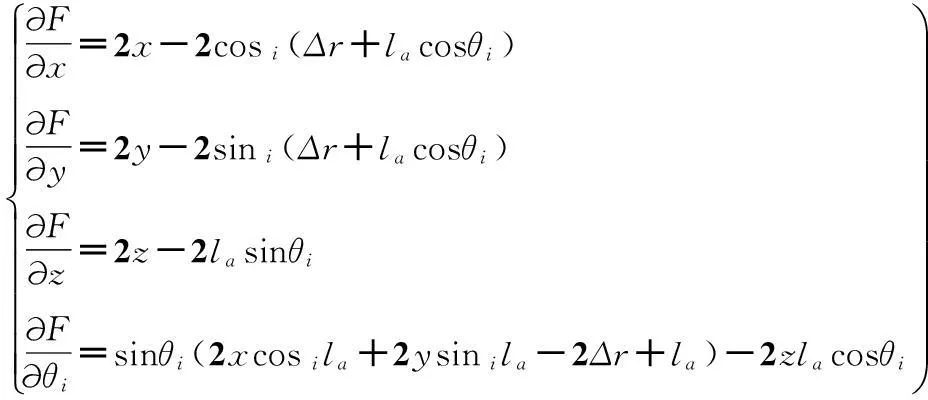
(12)

故可得式(13)：

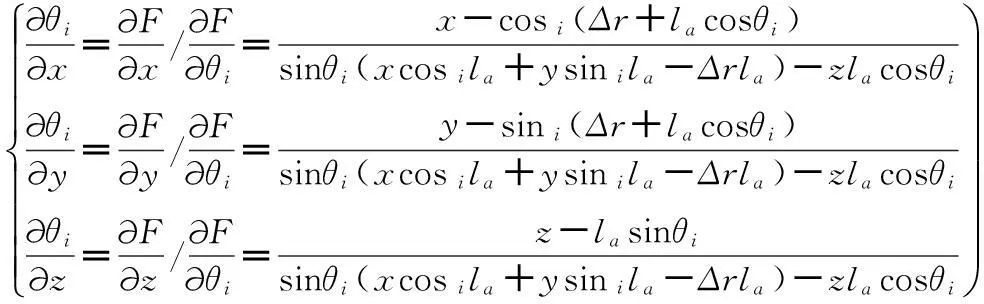
(13)

b) 求解重力参数G

根据手控器各运动部件之间的位置约束关系可得：

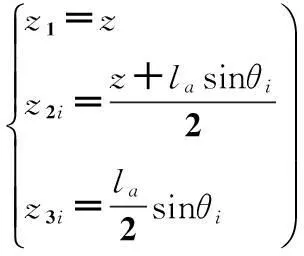
(14)

由以上分析得到的式(2)可求出手控器的重力参数G，式(2)中:

(15)

则:

(16)

将θi看作x,y,z的函数，θi=f(x,y,z)，故:

(17)

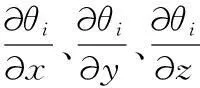
c) 重力补偿计算

根据上面的求解过程，使用VC++进行编程，对重力补偿计算进行程序化，且使用绘图插件实时绘制平衡力矩图。

3.2　基于ADAMS仿真分析的重力补偿研究

在基于静力学的计算过程中，对机构进行了简化处理，且未考虑轴承的摩擦力矩等因素对重力补偿造成的影响，该手控器转动副较多。为增加机构精度，在设计中部分转动副采用双列轴承，所以考虑轴承的摩擦对手控器的重力补偿有重要的意义。而在静力学计算过程中加入轴承的摩擦力会使计算变得极其繁琐，且无法计算。文中采用ADAMS进行仿真计算，研究手控器的重力补偿，并应用ADAMS仿真结果与计算结果进行对比，验证计算结果的正确性与可靠性。

在ADAMS中建立手控器的力学模型，添加质量信息、重力、运动副、驱动，在运动副上添加相应的摩擦力，根据手控器轴承型号61800，查阅相关资料可知，其摩擦系数u=0.0010~0.0015；采用在手控器三运动支链a2杆与电动机输出轴的转动副上添加相应的驱动。在静力学计算与ADAMS仿真过程中将电动机转角赋予同样的运动规律，以绘制平衡力矩曲线，对结果进行对比分析。

在ADAMS仿真分析中，手控器21处转动副均添加摩擦力矩，根据式(1)，手控器静力平衡的条件可以修改为：

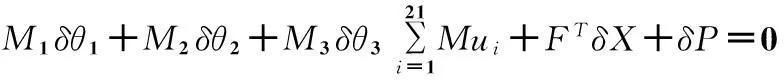
(18)

由式(18)可知，ADAMS仿真结果将小于静力学计算结果。

4结果分析

在静力学计算以及ADAMS仿真中，将三运动支链关节驱动运动规律设置为：θ1=0.01°×time，θ2=0.015°×time，θ3=0.02°×time，设置运动时间为1500s。ADAMS仿真及静力学计算结果分别如图6、图7所示。

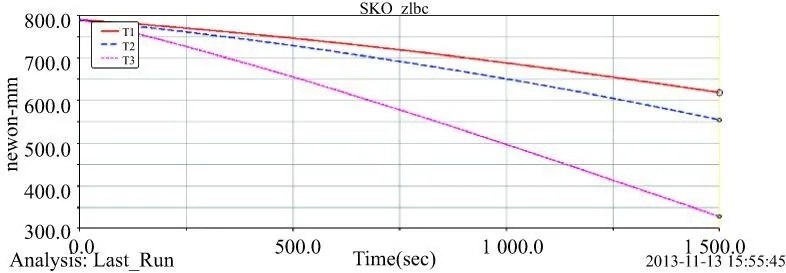
图6　ADAMS仿真结果

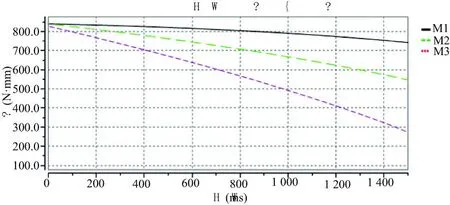
图7　静力学计算结果

对静力学计算与ADAMS仿真中的手控器赋予其他的运动规律，均可得到较为相似的曲线。对比静力学计算与ADAMS仿真分析结果可知其误差较小，且在手控器实际操作中，运用静力学计算结果进行实时补偿效果较好，操作者在操作过程中的疲劳感基本得到消除，试验验证了三自由度平动手控器重力补偿的可行性与有效性，重力补偿提高了手控器的操作性能。

参考文献:

[1] 宋爱国. 力觉临场感遥操作机器人(1):技术发展与现状[J]. 南京信息工程大学学报(自然科学版) , 2013，5(1) : 1-19.

[2] 崔建伟,宋爱国,黄惟一,等. 一种新型六自由度通用型手控器[J]. 中国机械工程，2005,16(4)：320-323.

[3] 崔建伟. 力觉临场感系统中的异构式手控器设计[D]. 南京：东南大学，2004.

[4] Soo S Lee, Jang M Lee. Design of a general purpose 6-DOF haptic interface[J]. Mechatronics 13(2003),2003: 697-722.

[5] 周龙江，宋爱国，曾庆军，等. 遥操作机器人手控器的研究进展[J]. 机器人技术与应用,2002,4:11-15.

[6] 杨强，孙志礼，闫明，等. 改进Delta并联机构运动可靠性分析[J]. 航空学报,2008,29(2):477-491.

[7] 程世利. 并联机构若干基本问题的研究[D]. 南京：南京航空航天大学，2011.

[8] Clavel R. Delta, a fast robot with parallel geometry[C]. Proceedings of the 18th International Symposium on Industrial Robot. 1988:91-100.

[9] 李长军. 面向外科手术的力反馈型遥操作主手研究[D]. 哈尔滨：哈尔滨工业大学，2010.

[10] 吴孟丽. 一种新型三自由度并联机构的设计理论与方法[D]. 天津：天津大学，2007.

[11] 艾青林，黄伟锋，张洪涛，等. 并联机器人刚度与静力学研究现状与进展[J]. 力学进展，2012,42(5)：583-592.

[12] 李俊峰. 理论力学[M]. 北京：清华大学出版社，2001：87-94.

Research on Gravity Compensation of 3-DOF Translation Hand Controller

LIU Shi-ping，YU Kun，LI Shi-qi，WANG Bo，SONG Fan

(School of Mechanical Engineering; Huazhong University of Science and Technology, Wuhan 430074, China)

Abstract:To design and manufacture 3-DOF translation hand controller, through static calculation and ADAMS simulation analysis, this paper finds out the driving torque of every electric motor，which is used to balance the self-gravity of hand controller in any position and applies the computed result to its operating process. The experiment proves that the gravity compensation can effectively eliminate the influence of the gravity of the hand controller on the operatons and their operating fatigue, thus improving its operation and efficiency.

Keywords:robot; man-machine interaction; hand controller; gravity compensation; static analysis; simulation

中图分类号：TH113

文献标志码：A

文章编号：1671-5276(2015)02-0155-04

作者简介：刘世平(1971-)，男，副教授，博士，研究领域：智能机械及仿真、遥操作、空间机械臂视觉测量与视觉伺服。

收稿日期：2014-11-04