多相离散随机介质模型及其探地雷达波场特征研究
2015-03-01郭士礼冀孟恩朱培民李修忠
郭士礼, 冀孟恩, 朱培民, 李修忠
1 河南工程学院资源与环境学院, 郑州 451191 2 河南高速公路试验检测有限公司, 郑州 450121 3 中国地质大学地球物理与空间信息学院, 武汉 430074 4 黄淮学院建筑工程学院, 河南 驻马店 463000
多相离散随机介质模型及其探地雷达波场特征研究
郭士礼1,2,3, 冀孟恩2, 朱培民3, 李修忠4*
1 河南工程学院资源与环境学院, 郑州 451191 2 河南高速公路试验检测有限公司, 郑州 450121 3 中国地质大学地球物理与空间信息学院, 武汉 430074 4 黄淮学院建筑工程学院, 河南 驻马店 463000
沥青混凝土是由骨料、沥青胶浆、空气按照一定的体积百分比混合而成的多相非匀质混合物,其骨料、沥青胶浆和空气的体积不等、形状各异、介电特性不同、空间位置随机分布,具有明显的多相、离散、随机介质特征.本文基于随机介质模型理论,(1)测量与统计了介电常数在典型沥青混凝土芯样空间上的随机分布统计特征;(2)估算了沥青混凝土介质的自相关函数及其特征参数(自相关长度、自相关角度等),确定其随机介质类型;(3)提出了量化约束下的多相离散随机介质建模算法,以混合型椭圆自相关函数为基础,构建了不同粗糙度因子的多相离散随机介质模型;(4)构建了不同空隙率的多相离散随机介质模型,正演模拟与对比分析了探地雷达波在均匀介质、连续型随机介质和多相离散随机介质中的传播特征.结果表明:多相离散随机介质模型不仅描述了沥青混凝土的多相、离散与空间随机分布统计特征,而且进一步描述了其各组成物质体积百分比,能更全面、准确地描述沥青混凝土的介质特征,同时也为描述其他类似材料或介质提供了新的方法和途径;在多相离散随机介质模型中,探地雷达波散射强烈,随机、无序传播的散射波相互叠加干涉,形成了明显的随机扰动和“噪声”,致使异常体反射波扭曲变形、不连续,降低了探地雷达回波的信噪比和分辨率.研究探地雷达波的随机扰动特征与多相离散随机介质模型参数之间的关系,将为定量评价多相离散随机介质的属性参数提供参考和帮助.
随机介质; 多相离散; 特征参数; 重构; 波场特征
1 引言
探地雷达方法具有高分辨率、高效率、连续、无损等优点,已成为浅层结构勘探领域最重要的物探方法之一,尤其是在公路工程、建筑工程等浅层工程质量无损检测工作中发挥了重要作用(Saarenketo and Scullion,2000;Maierhofer,2003;Alani et al., 2013;黄忠来和张建中,2013).我国高速公路结构层通常采用沥青混凝土面层加半刚性基层的形式,当探地雷达应用于公路结构层厚度检测与病害(如裂缝、脱空、不均匀沉降、疏松等)调查时,通常将公路结构层材料简化为均匀介质或层状均匀介质,并由此建立相应的公路工程质量探地雷达检测理论与资料处理解释方法(卢成明等,2007).而实际的公路结构层材料(如沥青混凝土、水泥稳定碎石等)是由多种物质按照一定的体积百分比组合而成的多相非匀质混合物(蔡迎春,2008).以沥青混凝土为例,它是由骨料、沥青胶浆、空气按照一定的体积百分比混合而成的多相非均质混合物,其骨料、沥青胶浆和空气的体积不等、粒径多尺度、几何形状各异、电磁性质不同,位置在空间上随机分布(吴丰收,2009;丁亮等,2012),具有明显的多相、离散、随机介质特性.自然界广泛存在的多孔介质通常也是多相离散随机介质(Cai and Yu, 2011).高频电磁波在多相离散随机介质中传播时,会发生散射,造成大量的不相干波至,致使接收波形也具有相应的随机特征(Jiang et al., 2013;戴前伟和王洪华,2013).尤其是路用探地雷达天线的主频较高,探测波长较短(约为最大粒径的3~5倍),散射相对较大,使得介电特性在介质空间上随机分布引起的波场变化被相对放大,将十分明显地影响高频电磁波的传播.因此,对于高频电磁波来说,沥青混凝土的物性参数变化剧烈,电磁散射严重,无法简化为均匀介质,而应依据电磁参数在沥青混凝土空间上具有多相、离散、随机分布的特征,建立更符合其实际情况的多相离散随机介质模型,数值模拟探地雷达波在其中的传播特征,为提高探地雷达探测分辨率、改进数据处理方法,以及定量解释工程材料介质属性提供理论基础和科学依据,具有重要的科学意义和应用价值.
作者采用钻孔取芯法获取了一些沥青混凝土芯样,利用矢量网络分析仪测量其主要组成物质的介电常数,得到其介电常数空间分布图,研究介电常数在芯样空间上的随机分布统计特征;然后,结合沥青混凝土各组成物质的体积百分比,提出了严格量化约束下的多相离散随机介质模型建模算法,构建与沥青混凝土实际情况更相符的多相离散随机介质模型,正演模拟与对比分析探地雷达波在均匀介质模型、连续型随机介质模型与多相离散随机介质模型中的波场特征.
2 随机介质模型理论
多相离散随机介质可运用随机介质模型理论来刻画.随机介质模型理论将介质的物性参数作为空间随机变量,基于统计学方法描述其空间随机分布特征.随机介质模型大致可分为平稳和非平稳两种类型,平稳随机介质模型由自相关函数、自相关长度、自相关角度、均值、标准差等统计量表征(徐涛等,2007).高斯型(Ergintav and Canitez,1997;赵迎月等,2013)、指数型(Ikelle et al., 1993)和混合型(奚先和姚姚,2002;Jiang et al., 2013)椭圆自相关函数被广泛用于构造随机介质模型,不同的自相关函数适用于不同的地质特征;在随机介质中,自相关长度描述非均匀异常在不同方向上的平均尺度,自相关角度描述非均匀异常的走向,均值描述随机介质的平均特性,标准差描述随机介质的离散程度.
平稳随机介质模型假定介质的统计特征为常量,存在许多局限性,不能完整地描述各种复杂、非平稳的实际介质.奚先和姚姚(2005)提出一种由空间变化的自相关函数(局部自相关函数)构造非平稳随机介质模型的新方法,该方法通过在水平方向和垂直方向上选择局部自相关长度,构建各种不同形式的非平稳随机介质模型.研究表明:非平稳随机介质模型能更加灵活地描述各种复杂、非均匀的实际介质.高斯型、指数型和混合型二维非平稳椭圆自相关函数表达式如下:
高斯型椭圆自相关函数:


(1)
指数型椭圆自相关函数:
(2)
混合型椭圆自相关函数:


上述二维非平稳椭圆自相关函数描述了局部自相关函数R(x′,y′,x1,y1)在大尺度上随空间坐标(x′,y′)缓慢变化.在二维非平稳随机介质中,全局坐标和局部坐标之间的关系如图1所示.

图1 二维非平稳随机介质中全局坐标与局部坐标的关系Fig.1 Relationship between global coordinate and local coordinate
在非平稳随机介质模型中,局部自相关长度a=a(x′,y′)、b=b(x′,y′)和方向角θ=θ(x′,y′)随空间坐标(x′,y′)缓慢变化,a=a(x′,y′)、b=b(x′,y′)和θ=θ(x′,y′)分别表示点(x′,y′)处随机介质在x、y方向上的自相关长度和自相关角度.对比上述公式,可以看出混合型椭圆自相关函数不仅综合了指数型(r=1)与高斯型(r=0)椭圆自相关函数的特点,而且通过粗糙度因子r能进一步拓展其模拟实际随机介质的类型和范围(郭乃川等,2012).
由于平稳和非平稳随机介质模型描述的介质物性参数在空间上连续地随机变化,故又称为连续型随机介质模型.多相离散随机介质的物性参数不仅在空间上具有多相、离散和随机分布特征,而且其各组成物质满足一定的体积百分比,因此上述连续型随机介质模型难以完整地描述多相离散随机介质,必须依据沥青混凝土物性参数的空间随机分布统计特征和各组成物质体积百分比,改进随机介质模型建模算法,才能构建更符合沥青混凝土实际情况的多相离散随机介质模型.
3 沥青混凝土的随机介质特性分析与模型参数估算
3.1 介电常数在沥青混凝土空间上的分布特征
介电常数是分析电磁波与介质相互作用的基础参数,统计、掌握介电常数在沥青混凝土空间上的随机分布统计特征,是重构沥青混凝土介质模型的基础.
作者钻取了豫西某高速公路沥青混凝土中面层芯样,对其进行横向切割,得到7 cm×7 cm的二维横切片,如图2a所示.采用E5071C型矢量网络分析仪(吴俊军等,2011),多次测量其骨料、沥青在0.5~2 GHz频段内的相对介电常数,取其均值,作为骨料和沥青的相对介电常数值,分别为εr=8.2、εr=2.8.由于沥青胶浆在沥青混凝土中的含量较少,分布零散,无法直接测量其介电常数,因此,本文依据沥青胶浆中沥青和矿粉的体积百分比及其介电常数,采用复折射率模型(Birchak et al., 1974)估算其等效介电常数为εr=5.44.
依据沥青混凝土的骨料、沥青胶浆和空气在照片中灰度级的不同,应用图像阈值分割技术将骨料、沥青胶浆与空气分割出来,赋予其相应的介电常数,得到沥青混凝土的介电常数空间分布图εr(x,y),如图2b所示.
基于介电常数空间分布图εr(x,y),可以统计出各组成物质的体积百分比(如骨料率Pg=77.86%、沥青胶浆率Pj=21.70%、空隙率Pk=0.43%),统计出相对介电常数的均值εmv=7.5694、标准差σ=1.2175等空间随机分布统计特征.
3.2 自相关函数及其特征参数的估算方法
自相关函数是体现随机介质空间分布特征和决定随机介质类型(Klimeš,2002;刘永霞等,2007)的重要参数.由维纳-辛钦定理可知,介电常数空间分布图εr(x,y)的功率谱与其自相关函数互为傅里叶变换对,由此可先计算介电常数空间分布图εr(x,y)的功率谱,再对其进行二维傅里叶逆变换,得到其自相关函数图像,然后进行归一化与二值化处理,提取
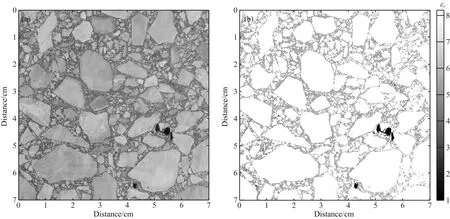
图2 沥青混凝土二维横向切片照片(a)及其介电常数空间分布图(b)Fig.2 Transverse profile of asphalt concrete (a) and its permittivity in spatial distribution image (b)
自相关函数在不同方向上的自相关长度、自相关角度等特征参数.
(1) 介电常数空间分布图εr(x,y)的功率谱
介电常数空间分布图εr(x,y)的功率谱可用下式计算(BalboaandGrzywacz,2003;AminandSubbalakshmi,2007):
(4)
(4)式中
(5)
式中,kx、ky分别为介电常数空间分布图x、y方向的空间频率,M、N分别为介电常数空间分布图x、y方向的采样点数.
(2)εr(x,y)对应的自相关函数Rε ε(x,y)
根据维纳-辛钦定理,介电常数空间分布图εr(x,y)的自相关函数Rε ε(x,y)是其功率谱Γ(kx,ky)的二维傅里叶逆变换,即
Rε ε(x,y)=IFFT2(Γ(kx,ky)),
(6)
介电常数空间分布图εr(x,y)对应的自相关函数Rε ε(x,y)如图3所示.
(3)归一化自相关函数
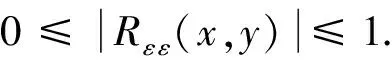
(4)提取自相关函数的特征参数
对于线性归一化后的自相关函数,其自相关长度为最大值1衰减至e-1的距离(Zhang and Sundararajan,2006).因此可将自相关函数值大于等于e-1的赋值为1,小于e-1的赋值为零(图5),以方便提取自相关函数在x、y方向上的自相关长度a、b和自相关角度θ等特征参数.
依据上述统计与估算方法,可得到介电常数空间分布图(图2b)的空间随机分布统计特征、自相关函数特征参数、各组成物质体积百分比等多相离散随机介质模型参数,如表1所示.

表1 多相离散随机介质模型参数Table 1 Model parameters of multiphase discrete random medium
4 多相离散随机介质模型建模算法与实例
4.1 多相离散随机介质模型建模算法
图5中的自相关函数形状近似于椭圆.我们计算了大量沥青混凝土切片的自相关函数,其形状均近似于椭圆,因此,我们认为沥青混凝土的自相关函数近似于椭圆自相关函数.用于构造随机介质模型的椭圆自相关函数主要有高斯型、指数型和混合型,
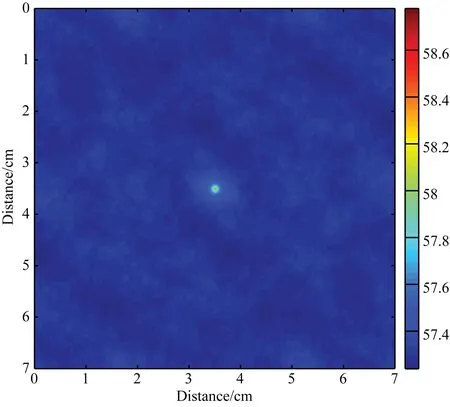
图3 自相关函数图像Fig.3 Auto correlation function image
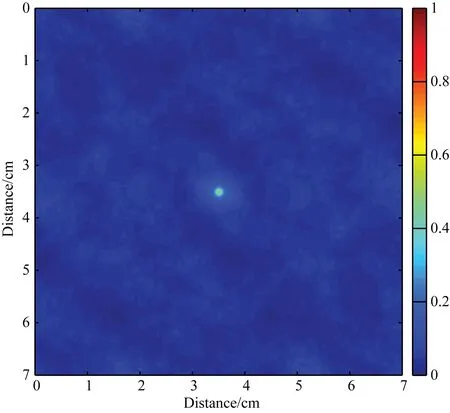
图4 归一化自相关函数图像Fig.4 Auto correlation function image after normalization

图5 二值化自相关函数图像(图b为图a虚线内部分) Fig.5 Auto correlation function image after binary-conversion (figure b is the area bounded by dotted line in figure a)
鉴于混合型椭圆自相关函数可以通过粗糙度因子r进一步拓展其模拟实际随机介质的类型和范围,本文以混合型椭圆自相关函数为基础构建多相离散随机介质模型.
依据介电常数在沥青混凝土空间上的随机分布统计特征量及其自相关函数特征参数,同时结合沥青混凝土各组分的体积百分比,改进连续型随机介质模型建模算法,建立能准确描述工程材料电磁参数空间随机分布统计特征和各组成物质体积百分比量化约束的多相离散随机介质模型建模算法.多相离散随机介质模型的具体建模方法如下:
(1) 依据上述介电常数空间分布图自相关函数的自相关长度a、b与自相关角度θ等特征参数的估算结果,选择合适的粗糙度因子r,对混合型椭圆自相关函数RM(x,y)进行二维傅立叶变换,得到随机过程功率谱RM(kx,ky).
(2) 生成随机信息.用随机数发生器生成在[0,2π)区间均匀分布的独立二维随机场φ(kx,ky).
(3) 生成随机功率谱函数.根据随机过程理论,随机过程功率谱RM(kx,ky)与二维随机场φ(kx,ky)的乘积就是随机功率谱函数.
(4) 对随机功率谱函数进行二维傅立叶逆变换,求得随机扰动.
(5) 对随机扰动的均值和标准差进行规范化,获得以RM(x,y)为自相关函数、具有指定均值和标准差的连续型二维随机介质模型.
(6) 确定多相离散随机介质模型参数的局部尺寸R,设沥青混凝土中的骨料体积百分比为Pg,空气体积百分比为Pk,则沥青胶浆体积百分比为Pj=1-Pg-Pk,及骨料、沥青胶浆和空气的相对介电常数ε1=8.2、ε2=5.44、ε3=1.以R×R为局部区域分割模型.进入第一个局部区域.
(7) 按照模型值的大小,依次从大到小腐蚀局部区域内的网格点,把网格点的值赋值为ε1,并判断该局部区域内是否满足骨料体积百分比Pg,满足则转入步骤(8),否则重新执行步骤(7).
(8) 按照模型值大小,依次从小到大腐蚀局部区域内的网格点,将该网格点的值赋值为ε3,然后判断是否满足空气体积百分比Pk,不满足重新执行(8),满足则转入下一个局部区域,执行(7)、(8),直至所有局部区域都满足骨料率Pg和空隙率Pk.
(9) 循环遍历整个模型,将所有模型值不是ε1或ε3的网格点赋值为ε2.至此,获得骨料体积百分比为Pg、空气体积百分比为Pk、沥青胶浆体积百分比为Pj,且骨料、空气具有自组织结构的多相离散随机介质模型.
以表1中的沥青混凝土介电常数空间分布统计特征量(均值、标准差)与自相关函数特征参数(自相关长度、自相关角度)为模型参数,基于粗糙度因子r=2.5的混合型椭圆自相关函数,根据上述建模方法中的步骤(1)—(5),建立连续型随机介质模型,如图6所示.在图6的基础上,结合各组成物质体积含量百分比,根据上述建模方法中的步骤(6)—(9),建立既描述沥青混凝土介电常数空间随机分布统计特征,又符合其体积百分比量化约束的多相离散随机介质模型,如图7所示.图7较好地体现了沥青混凝土组织结构的特征,即骨料起骨架作用,沥青胶浆起胶结填充作用.

图6 连续型随机介质模型Fig.6 Continuous random medium model
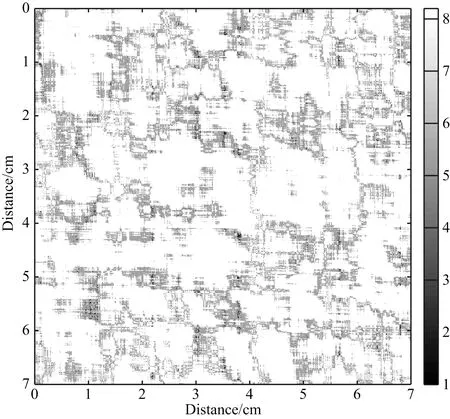
图7 多相离散随机介质模型Fig.7 Multiphase discrete random medium model
以表1中的介电常数空间分布统计特征量、各组成物质含量百分比以及自相关函数特征参数为模型参数,依次改变混合型椭圆自相关函数中粗糙度因子r的大小,建立粗糙度因子r=0、0.1、0.2…5的多相离散随机介质模型.部分多相离散随机介质模型如图8所示.从图8中可以看出,当其他模型参数固定不变时,混合型椭圆自相关函数的粗糙度因子r越小,其生成的多相离散随机介质模型值越分散;粗糙度因子r越大,多相离散随机介质模型值聚集效应越好.随着粗糙度因子r的不断变大,其生成的多相离散随机介质模型的聚集效应越好,相当于骨料的粒径越大.为了比较上述多相离散随机介质模型与沥青混凝土介电常数空间分布图(图2b)之间的相似程度,本文估算了上述多相离散随机介质模型的自相关函数及其特征参数,并计算了它们与介电常数空间分布图自相关函数之间的相关系数.相关系数随粗糙度因子r的变化曲线如图9所示.
从图9中可以看出,当粗糙度因子r=2.5时,其多相离散随机介质模型的自相关函数图像与沥青混凝土自相关函数图像之间的相关系数最大、相关性最好、相似性最大.故,本文将粗糙度因子r=2.5的混合型椭圆自相关函数作为沥青混凝土介电常数空间分布图对应的自相关函数表达式.
4.2 多相离散随机介质模型建模实例
依据上述介电常数在沥青混凝土空间上的统计

图8 粗糙度因子对多相离散随机介质模型的影响(a) 粗糙度因子r=1; (b) 粗糙度因子r=2; (c) 粗糙度因子r=3; (d) 粗糙度因子r=4.Fig.8 Impact of roughness factor on multiphase discrete random medium models
特征量、自相关函数特征参数、混合型椭圆自相关函数粗糙度因子的估算结果,依据多相离散随机介质模型建模算法,可以建立任意体积百分比的多相离散随机介质模型.下面以不同空隙率的多相离散随机介质模型为例进行介绍.
空隙率是指空气在沥青混凝土中的体积百分比,它是影响路面使用寿命和变形性能的最重要因素.对于公路沥青混凝土路面,其油石比相对稳定(钟燕辉等,2007),当空隙率不断增大时,其骨料与沥青胶浆的体积百分比成比例减小.以表1中的介电常数空间分布统计特征(均值、标准差)与自相关函数特征参数(自相关长度、自相关角度)为模型参数,基于混合型椭圆自相关函数(粗糙度因子r=2.5),建立空隙率分别为2%、4%、6%、8%的多相离散随机介质模型(图10),表2给出了不同空隙率的多相离散随机介质中各组成物质的体积百分比.

图10 不同空隙率的多相离散随机介质模型(a) 空隙率=2%; (b) 空隙率=4%; (c) 空隙率=6%; (d) 空隙率=8%.Fig.10 Multiphase discrete random medium models with different porosity
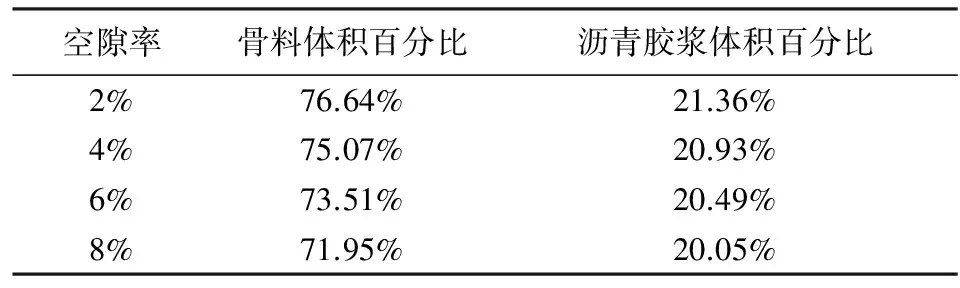
表2 不同空隙率的多相离散随机介质模型各组成物质体积百分比Table 2 Volume fractions of composition of multiphase discrete random medium models with different porosity
5 多相离散随机介质模型的正演模拟
5.1 多相离散随机介质与均匀介质的正演模拟分析
为了研究探地雷达波在多相离散随机介质中的传播特征,本文基于时域有限差分方法对多相离散随机介质模型(空隙率=4%)及其均值对应的均匀介质模型进行探地雷达正演模拟.模型网格总数为500×600,空间网格步长为0.1 cm,模型上部区域为空气介质,厚度为10 cm;模型中部区域为多相离散随机介质或其对应的均匀介质,厚度为40 cm,中间有一宽度为0.5 cm的垂向裂缝,裂缝的顶、底端距上、下介质分界面均为15 cm;模型下部区域为均匀无耗介质(εr=9),厚度为10 cm.GPR波脉冲激励源的中心频率为1500 MHz.图11为探地雷达波在多相离散随机介质和均匀介质中3 ns时刻的波场快照.可以看出,在多相离散随机介质中,探地雷达波散射强烈,随机、无序传播的散射波相互叠加,致使裂缝顶、底端的反射波扭曲变形、不连续,不易辨识;而在均匀介质中,探地雷达波未发生散射,波形比较规则,裂缝顶、底端的反射波清晰可见.
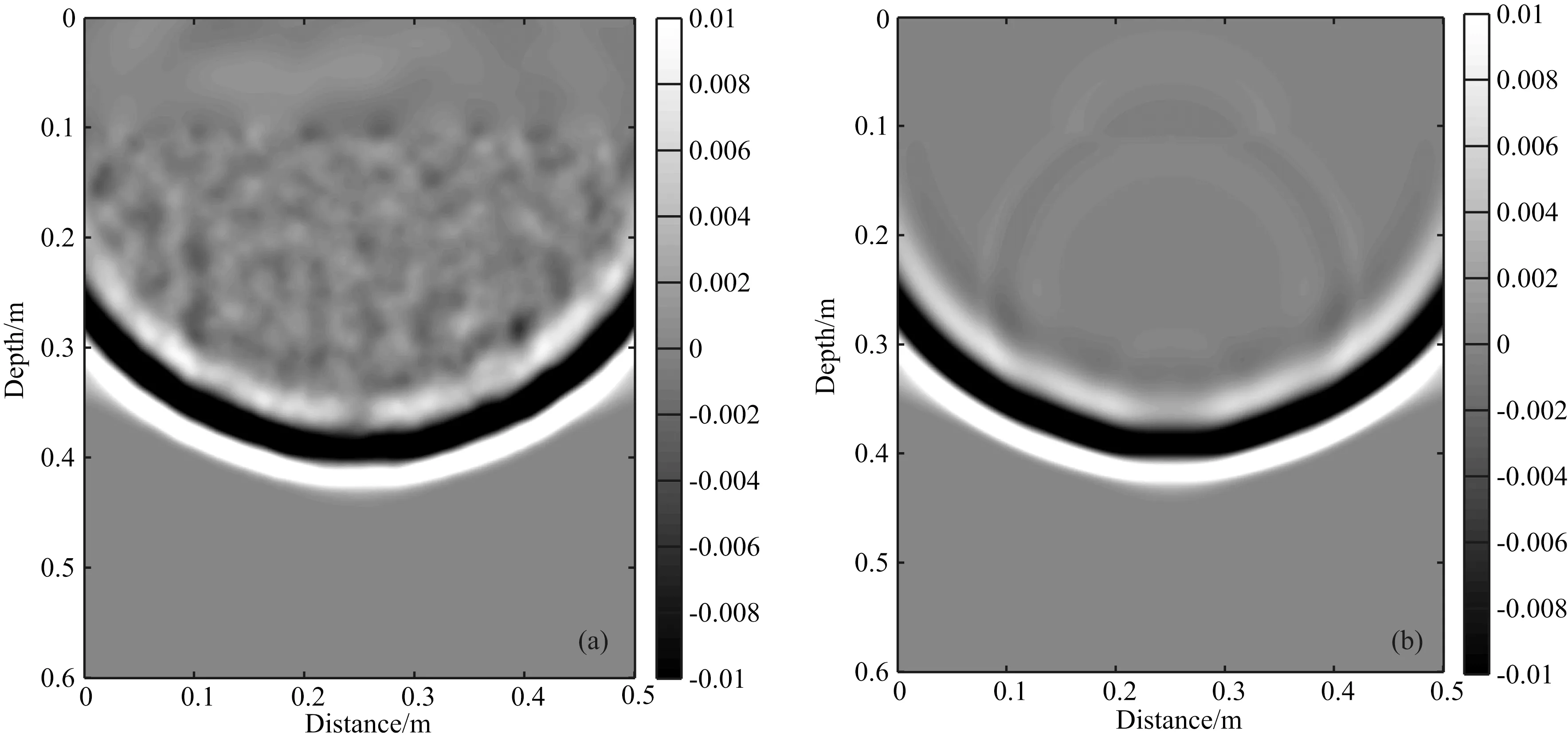
图11 多相离散随机介质模型(a)与均匀介质模型(b)的波场快照图Fig.11 Wave field snapshots of multiphase discrete random medium model (a) and homogeneous medium model (b)
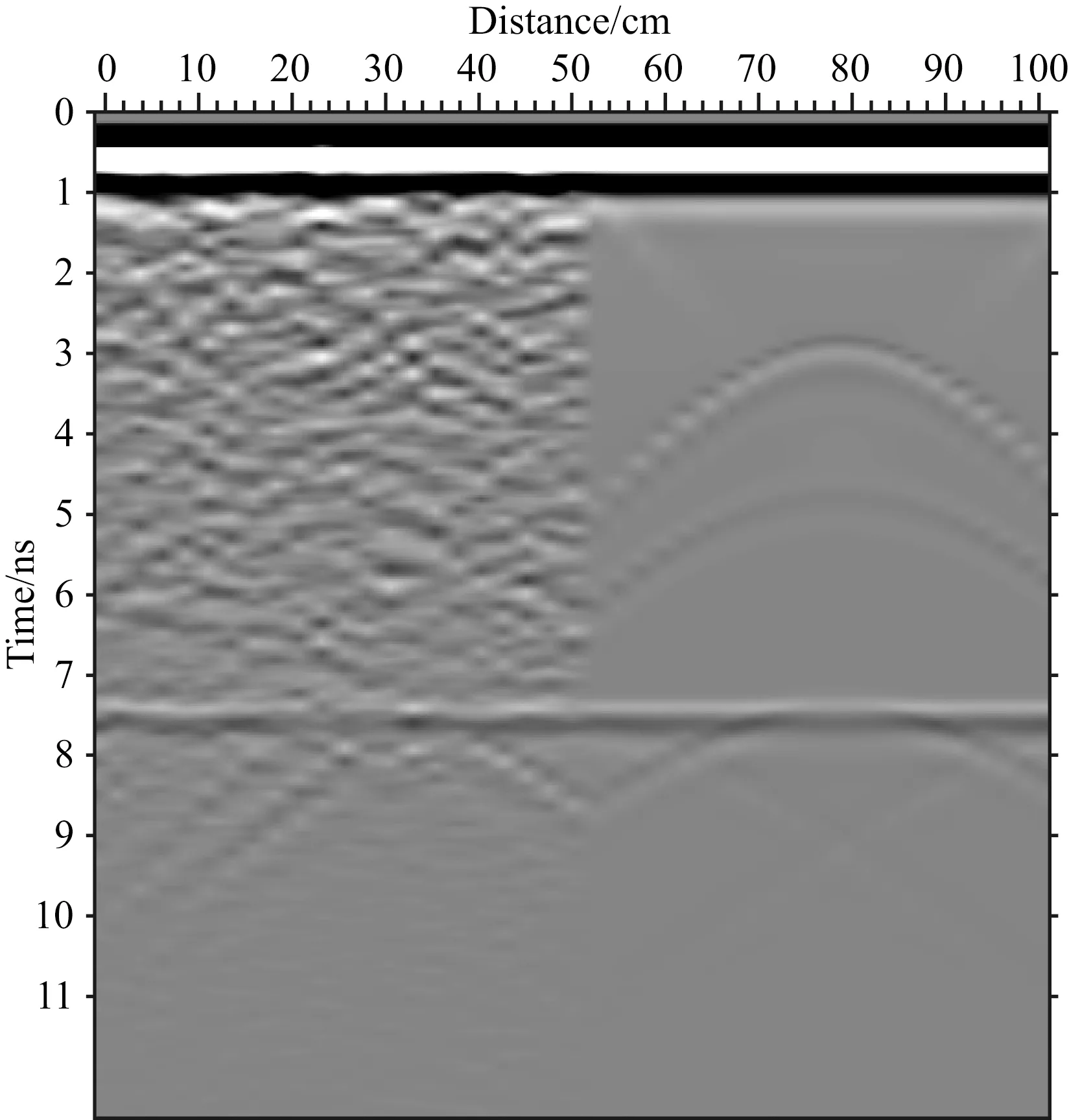
图12 多相离散随机介质模型和均匀介质模型正演模拟剖面图Fig.12 GPR profiles of multiphase discrete random medium model and homogeneous medium model
为便于对比分析,本文将多相离散随机介质和均匀介质正演模拟结果放在同一个剖面图中,如图12所示.图中0~50 cm为多相离散随机介质正演模拟剖面图,其具有明显的随机扰动和“噪声”,裂缝顶、底端反射波双曲线不易辨识,下层界面反射波同相轴扭曲变形、不连续且振幅较弱.这源于探地雷达波在多相离散随机介质中发生了散射,部分散射波返回地面,为接收天线接收,降低了探地雷达回波的信噪比和分辨率;图中51~100 cm为均匀介质正演模拟剖面图,其裂缝顶、底端绕射波双曲线清晰可见,下层界面反射波同相轴清晰平直、振幅较强.
5.2 连续型随机介质与多相离散随机介质的正演模拟分析
与连续型随机介质模型相比,多相离散随机介质模型不仅描述了沥青混凝土空间上的多相、离散与随机分布统计特征(如自相关函数、均值、标准差等),而且进一步描述了各组成物质的体积百分比,因此,能更全面、准确地描述沥青混凝土这类复杂的多相离散随机介质.以表2为建模参数,构建连续型随机介质模型及其对应的多相离散随机介质模型,模拟与分析探地雷达波在连续型随机介质和多相离散随机介质中的传播特征.正演模拟参数设置与5.1节的相同,仅将模型中部区域更换为连续型随机介质模型或多相离散随机介质模型.图13为探地雷达波在连续型随机介质和多相离散随机介质中3 ns时刻的波场快照.图14为连续型随机介质和多相离散随机介质正演模拟剖面,图中0~50 cm为连续型随机介质的正演模拟剖面图,51~100 cm为多相离散随机介质的正演模拟剖面图.
从图13、14中可以看出,(1)探地雷达波在连续型随机介质和多相离散随机介质中均发生了散射,随机传播的散射波相互叠加,形成了随机扰动和“噪声”,致使裂缝顶、底端反射波发生了扭曲变形,介质分界面反射波同相轴错断、不连续; (2)与多相离散随机介质相比,探地雷达波在连续型随机介质中的散射更强烈,产生的随机扰动更大、“噪声”更强、异常体反射波扭曲变形更大.
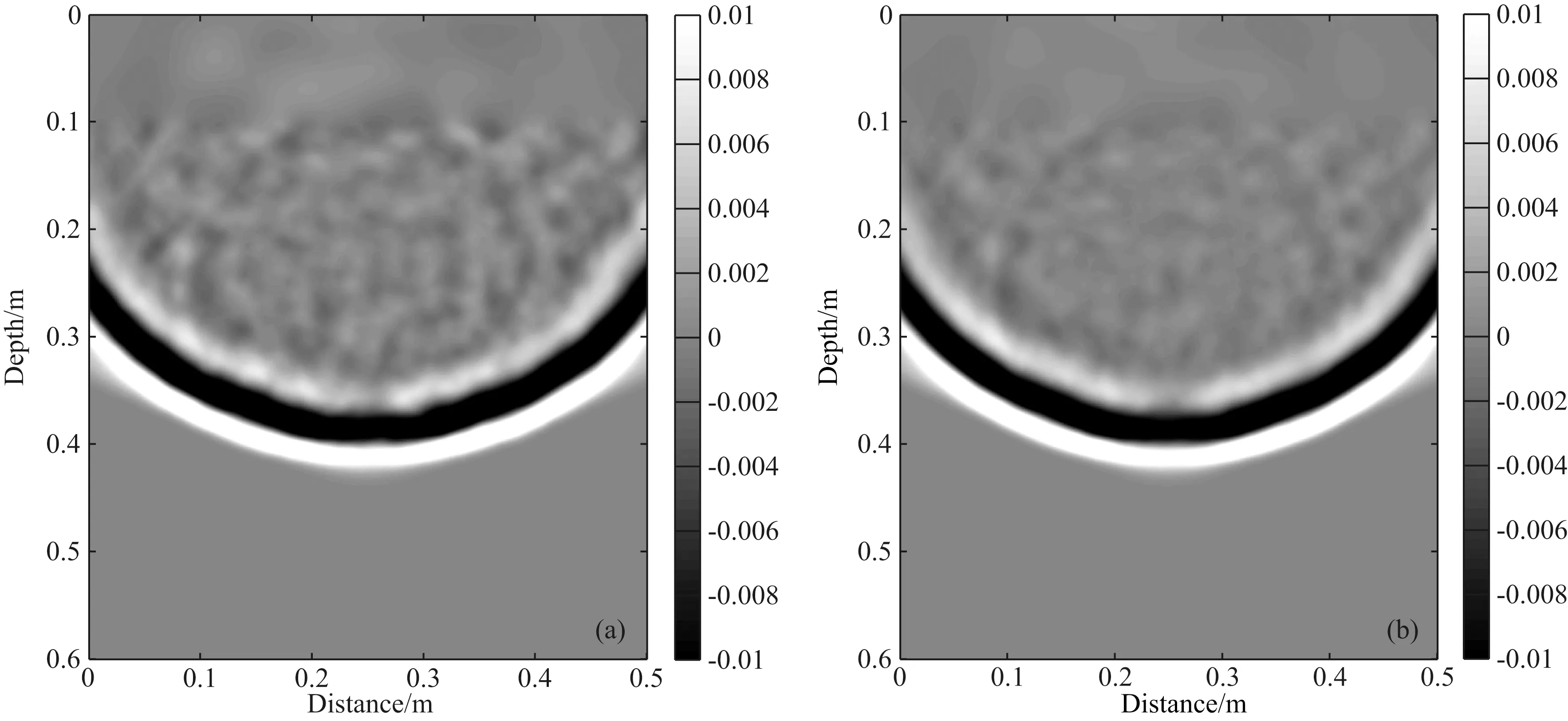
图13 连续型随机介质模型(a)与多相离散随机介质模型(b)的波场快照图Fig.13 Wave field snapshots of continuous random medium model (a) and multiphase discrete random medium model (b)
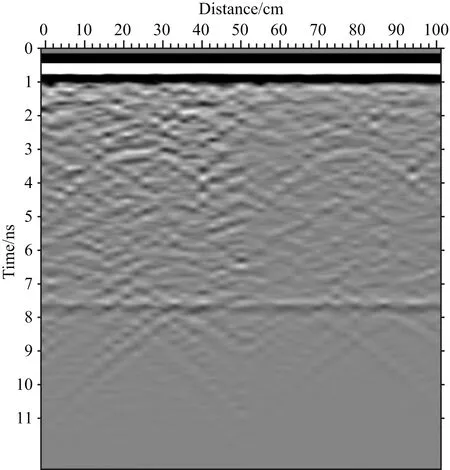
图14 连续型随机介质模型和多相离散随机介质模型正演模拟剖面图Fig.14 GPR profiles of continuous random medium model and multiphase discrete random medium model
在沥青混凝土探地雷达实测资料解释中,通常将这种由于多相离散随机介质的非均匀性造成的随机扰动当作“噪声”进行处理,无形中放弃了大量的、潜在的、有价值的信息.研究和利用这些信息,相信能提高探地雷达的分辨能力,以分辨出更多的材料属性信息和隐蔽病害信息.
6 结论
本文将沥青混凝土视作多相离散随机介质,通过芯样,研究了其介电常数在空间上的随机分布统计特征,估算了其自相关函数及其特征参数,提出了量化约束的多相离散随机介质模型建模算法,建立了不同空隙率的多相离散随机介质模型,正演模拟与对比分析了探地雷达波在均匀介质模型、连续型随机介质模型与多相离散随机介质模型中的波场特征,得到以下结论:
(1) 沥青混凝土的介电常数在空间上具有多相、离散、随机分布特征,是典型的多相离散随机介质,其自相关函数近似于椭圆自相关函数;
(2) 本文提出了多相离散随机介质模型建模算法,建模结果表明:多相离散随机介质模型不仅描述了介电常数在沥青混凝土空间上的多相、离散和随机分布统计特征,而且又与其各组成物质的体积百分比相符,能更全面、准确地描述沥青混凝土这种复杂的非均匀混合物介质类型,同时该模型也为描述其他类似材料或介质提供了新的方法和途径;
(3) 探地雷达波在多相离散随机介质中传播时存在强烈的散射现象,随机、无序传播的散射波相互干涉叠加,致使接收波形也具有相应的随机扰动特征和“噪声”,研究探地雷达回波随机扰动特征与多相离散随机介质模型参数之间的关系,将为定量评价多相离散随机介质属性参数提供参考和帮助.
致谢 感谢两位评审专家对本论文的认真审阅及建设性修改意见.
Amin P, Subbalakshmi K P. 2007. Detecting hidden messages using image power spectrum. ∥ ICIP 2007 Conference and Exhibition Extended Abstracts, 1: I-421-I-424.Alani A M, Aboutalebi M, Kilic G. 2013. Applications of ground penetrating radar (GPR) in bridge deck monitoring and assessment.JournalofAppliedGeophysics, 97: 45-54, doi: 10.1016/j.jappgeo.2013.04.009.
Balboa R M, Grzywacz N M. 2003. Power spectra and distribution of contrasts of natural images from different habitats.VisionResearch, 43(24): 2527-2537, doi: 10.1016/S0042-6989(03)00471-1.
Birchak J R, Gardner C G, Hipp J E, et al. 1974. High dielectric constant microwave probes for sensing soil moisture.ProceedingsoftheIEEE, 62(1): 93-98, doi: 10.1109/PROC.1974.9388.Cai J C, Yu B M. 2011. A discussion of the effect of tortuosity on the capillary imbibition in porous media.TransportinPorousMedia, 89(2): 251-263.
Cai Y C. 2008. Inverse analysis of dielectric properties for layered inhomogeneous media [Ph. D. thesis] (in Chinese). Dalian: Dalian University of Technology.
Dai Q W, Wang H H. 2013. Element free method forward modeling of GPR based on random medium model.TheChineseJournalofNonferrousMetals(in Chinese), 23(9): 2436-2443.
Ding L, Han B, Liu R Z, et al. 2012. Inversion imaging method for concrete non-destructive testing based on GPR.ChineseJ.Geophys. (in Chinese), 55(1): 317-326, doi: 10.6038/j.issn.0001-5733.2012.01.032.
Ergintav S, Canitez N. 1997. Modeling of multi-scale media in discrete form.JournalofSeismicExploration, 6(1): 77-96.
Guo N C, Wang S X, Dong C H, et al. 2012. Description of small scale inhomogeneities in seismic prospecting and long-wavelength theory.ChineseJ.Geophys. (in Chinese), 55(7): 2385-2401, doi: 10.6038/j.issn.0001-5733.2012.07.023.
Huang Z L, Zhang J Z. 2013. An inversion method for geometric and electric parameters of layered media using spectrum of GPR signal.ChineseJ.Geophys. (in Chinese), 56(4): 1381-1391, doi: 10.6038/cjg20130432.
Ikelle L T, Yung S K, Daube F. 1993. 2-D random media with ellipsoidal autocorrelation functions.Geophysics, 58(9): 1359-1372, doi: 10.1190/1.1443518.Jiang Z M, Zeng Z F, Li J, et al. 2013. Simulation and analysis of GPR signal based on stochastic media model with an ellipsoidal autocorrelation function.JournalofAppliedGeophysics, 99: 91-97, doi: 10.1016/j.jappgeo.2013.08.005.
Klimeš L. 2002. Correlation functions of random media.PureandAppliedGeophysics, 159(7-8): 1811-1831, doi: 10.1007/s00024-002-8710-2.
Liu Y X, Xu T, Zhao B, et al. 2007. Seismic sounding of anisotropic self-similar self-organized medium.ChineseJ.Geophys. (in Chinese), 50(1): 221-232.
Lu C M, Qin Z, Zhu H L, et al. 2007. Practical methods for detection of concealed cracks in highway pavement using ground penetrating radar data.ChineseJ.Geophys. (in Chinese), 50(5): 1558-1568.Maierhofer C. 2003. Nondestructive evaluation of concrete infrastructure with ground penetrating radar.JournalofMaterialsinCivilEngineering, 15(3): 287-297, doi: 10.1061/(ASCE)0899-1561(2003)15: 3(287).
Saarenketo T, Scullion T. 2000. Road evaluation with ground penetrating radar.JournalofAppliedGeophysics, 43(2-4): 119-138, doi: 10.1016/S0926-9851(99)00052-X.
Wu F S. 2009. A study of ground penetrating radar methods and techniques in concrete detection [Ph. D. thesis] (in Chinese). Changchun: Jilin University.
Wu J J, Liu S X, Dong H, et al. 2011. Permittivity measurement for rock and ore samples by open-ended coaxial method.ChineseJ.Geophys. (in Chinese), 54(2): 457-465, doi: 10.3969/j.issn.0001-5733.2011.02.024.
Xi X, Yao Y. 2002. Simulations of random medium model and intermixed random medium.EarthScience-JournalofChinaUniversityofGeosciences(in Chinese), 27(1): 67-71.
Xi X, Yao Y. 2005. Non-stationary random medium model.OilGeophysicalProspecting(in Chinese), 40(1):71-75.
Xu T, Ning J R, Liu C C, et al. 2007. Influence of the self-organization of the earth interior upon the traveltime and amplitude of seismic wave.ChineseJ.Geophys. (in Chinese), 50(4): 1174-1181, doi: 10.3321/j.issn:0001-5733.2007.04.026.
Zhang Y L, Sundararajan S. 2006. Generating random surfaces with desired autocorrelation length.AppliedPhysicsLetters, 88(14): 141903, doi: 10.1063/1.2191882 .
Zhao Y Y, Gu H M, Wang Y, et al. 2013. Research on constructing clastic reservoir seismic geologic model under no well condition.ChineseJ.Geophys. (in Chinese), 56(6): 2055-2064, doi: 10.6038/cjg20130626.Zhong Y H, Li Q, Chen Z P, et al. 2007. A study on application of GPR segregation detection of asphalt concrete pavement.Highway(in Chinese), (4):117-123.
附中文参考文献
蔡迎春. 2008. 层状非均匀介质介电特性反演分析[博士论文]. 大连: 大连理工大学.
戴前伟, 王洪华. 2013. 基于随机介质模型的GPR无单元法正演模拟. 中国有色金属学报, 23(9): 2436-2443.
丁亮, 韩波, 刘润泽等. 2012. 基于探地雷达的混凝土无损检测反演成像方法. 地球物理学报, 55(1): 317-326, doi: 10.6038/j.issn.0001-5733.2012.01.032.
郭乃川, 王尚旭, 董春晖等. 2012. 地震勘探中小尺度非均匀性的描述及长波长理论. 地球物理学报, 55(7): 2385-2401, doi: 10.6038/j.issn.0001-5733.2012.07.023.
黄忠来, 张建中. 2013. 利用探地雷达频谱反演层状介质几何与电性参数. 地球物理学报, 56(4): 1381-1391, doi: 10.6038/cjg20130432.
卢成明, 秦臻, 朱海龙等. 2007. 探地雷达检测公路结构层隐含裂缝实用方法研究. 地球物理学报, 50(5): 1558-1568.
刘永霞, 徐涛, 赵兵等. 2007. 自相似型各向异性自组织介质中地震波场动力学响应.地球物理学报, 50(1): 221-232.
吴丰收. 2009. 混凝土探测中探地雷达方法技术应用研究[博士论文]. 长春: 吉林大学.
吴俊军, 刘四新, 董航等. 2011. 基于开口同轴法的岩矿石样品介电常数测试. 地球物理学报, 54(2): 457-465, doi: 10.3969/j.issn.0001-5733.2011.02.024.
奚先, 姚姚. 2002. 随机介质模型的模拟与混合型随机介质. 地球科学-中国地质大学学报, 27(1): 67-71.
奚先, 姚姚. 2005. 非平稳随机介质模型. 石油地球物理勘探, 40(1): 71-75.
徐涛, 宁俊瑞, 刘春成等. 2007. 地球介质自组织性对地震波走时和振幅的影响. 地球物理学报, 50(4): 1174-1181, doi: 10.3321/j.issn:0001-5733.2007.04.026.
赵迎月, 顾汉明, 汪勇等. 2013. 无井条件下建立碎屑岩储层地震地质模型研究. 地球物理学报, 56(6): 2055-2064, doi: 10.6038/cjg20130626.
钟燕辉, 李强, 陈忠平等. 2007. 路面雷达在沥青混凝土路面离析检测中的应用研究. 公路, (4): 117-123.
(本文编辑 胡素芳)
Study on multiphase discrete random medium model and its GPR wave field characteristics
GUO Shi-Li1,2,3, JI Meng-En2, ZHU Pei-Min3, LI Xiu-Zhong4*
1CollegeofResourceandEnvironment,HenanInstituteofEngineering,Zhengzhou451191,China2HenanHighwayTestDetectionCo.,Ltd,Zhengzhou450121,China3InstituteofGeophysicsandGeomatics,ChinaUniversityofGeosciences,Wuhan430074,China4CollegeofArchitectureEngineering,HuanghuaiUniversity,ZhumadianHenan463000,China
Asphalt concrete is a type of multiphase, heterogeneous mixture. It is composed of aggregate, asphalt mortar and air with different volume fraction. Aggregate, asphalt mortar and air usually have different sizes, shapes, dielectric properties, and distribute randomly in space. Asphalt concrete has typical features of multiphase, discreteness and randomness. Scattering waves appear when high-frequency electromagnetic waves propagate in such medium. Thus, asphalt concrete cannot be simplified as homogeneous medium, but as multiphase discrete random medium and construct models based on the statistical characteristics of spatial random distribution of dielectric constant and volume fraction of each component of asphalt concrete, and study the propagation characteristics of high-frequency ground penetrating radar wave in such model by numerical simulation.This paper is based on random medium theory, (1) we measured the dielectric constants of the asphalt concrete samples, and computed the statistical characteristics (such as mean values, standard deviations) of spatial random distribution of dielectric constants and the volume fraction of each component; (2) we calculated the autocorrelation function of asphalt concrete based on Wiener-Khintchine theorem, and extracted its characteristic parameters (such as autocorrelation length, autocorrelation angle), and then classified the type of random media; (3) we developed the modeling algorithm of multiphase discrete random medium under quantization constrain, and constructed multiphase discrete random medium model based on intermixed elliptic autocorrelation function. Additionally, we studied the propagation characteristics of ground penetrating radar wave in multiphase discrete random medium model and compared the model with homogeneous medium model and continuous random medium model using numerical simulation.The calculated results show that the autocorrelation functions of a large number of asphalt concrete sections are approximate to ellipsoidal autocorrelation functions, which provide the foundation for using random medium theory to describe asphalt concrete. The multiphase discrete random medium model that is built by the modeling algorithm presented in this paper not only describes the statistical characteristics of spatial random distribution of asphalt concrete, but also describe the volume fractions of its composition when compare with homogeneous model and continuous random medium model. For multiphase discrete random medium model and continuous random medium model, ground penetrating radar wave has strong scattering phenomenon. Random and disorderly scattering waves overlie and interfere with each other, which resulting random perturbations and noise in received waves. The reflected waves from anomalous body are with distortion and discontinuity and reduce the signal to noise ratio and resolution of ground penetrating radar data. When multiphase discrete random medium model and continuous random medium model have the same given model parameters, ground penetrating radar waves have stronger scattering in continuous random medium model.The study reveals that the multiphase discrete random medium model can describe asphalt concrete more comprehensive and precise than homogeneous medium model and continuous random medium model. The multiphase discrete random medium model also provides a new way for studying similar media or materials. The radar profile is more consistent with the field measured data, and more conducive to guide the interpretation of the ground penetrating radar profile data. In the future, we will construct some multiphase discrete random medium models with different porosity parameters to study its effective permittivity and wave field features through numerical simulations, and explore the relations between the permittivity and wave field for quantitative interpretation of porosities of asphalt concrete for ground penetrating radar.
Random medium; Multiphase discrete; Model parameters; Reconstruction; Wave field characteristics
河南省高等学校重点科研项目(15A170005),河南工程学院博士基金(D2014008)与河南省科技重点攻关项目(112102310648)联合资助.
郭士礼,男,1982年生,博士,讲师,2013年7月博士毕业于中国地质大学(武汉)地球物理与空间信息学院,现任教于河南工程学院资源与环境学院,主要从事探地雷达理论与应用方面的教学与研究工作.E-mail:guo_ccnu@qq.com
*通讯作者李修忠,男,1964年生,博士,教授,主要从事工程质量无损检测理论与方法研究.E-mail:hhxylxz@163.com
10.6038/cjg20150813.
10.6038/cjg20150813
P631
2014-12-02,2015-06-28收修定稿
郭士礼, 冀孟恩, 朱培民等. 2015. 多相离散随机介质模型及其探地雷达波场特征研究.地球物理学报,58(8):2779-2791,
Guo S L, Ji M E, Zhu P M, et al. 2015. Study on multiphase discrete random medium model and its GPR wave field characteristics.ChineseJ.Geophys. (in Chinese),58(8):2779-2791,doi:10.6038/cjg20150813.
