一种基于RFM模型的新型协同过滤个性化推荐算法

张 宁，范崇睿，张 岩

（1.北京石油化工学院 北京 102617；2.北京航空航天大学 北京 102206；3.北京化工大学 北京 100029）

1 引言

随着互联网技术的迅猛发展，电子商务因其方便快捷的优点得到了人们的广泛关注。但随着商品资源数量的增长，顾客在网络购物方面很难方便、快捷地找到满意的商品。为帮助广大顾客迅速找到其所需要的商品，同时给商家带来更高的利润，个性化服务逐渐成为行业发展面临的一个关键问题。作为当前解决信息超载问题最有效的工具之一，数据挖掘技术应运而生，而个性化推荐技术正是此技术中一个重要的体现[1,2]。这种致力于帮助电商网站为顾客购物提供完全个性化服务的智能平台，在为顾客带来方便、快捷的同时，也为商家带来了巨大的利益。但随着商品信息的细化及客户对推荐内容要求的提高，目前应用的几种常用推荐技术的不足愈发明显，如推荐精度不高、效率过低、新商品或购买率较低的商品不能及时推荐给顾客等[3]。如何满足顾客的需求，向他们推荐符合其购物习惯或偏好的商品已成为当前推荐算法的首要问题之一。研究推荐系统在实际中的应用，无论是对于商家自身，还是顾客乃至社会，都具有很高的经济价值和实际意义。

国外的很多研究学者对于个性化推荐技术的不断研究，大大地推动了推荐技术自身的快速发展。Ahn H J等人提出了一种新颖的相似度评估方法[4]，精确了目标用户最近邻的求解，经实验验证，该方法有效地解决了传统相似度计算过程中最近邻求解不准确的问题，有效提高了推荐算法的推荐质量；Lemine D和Huang Z等人分别应用了SLopeOne算法[5]和用户行为分析法[6]，对稀疏的评分矩阵进行了有效的填充处理，并得到了很好的效果；Chang H Y等人将神经网络技术应用于传统的协同过滤算法中，同样提高了推荐质量[7]。此外，Deshpande、Kim H N等人也都提出了自己的改进思路，为推荐技术做出了贡献[8～10]。

近年来，我国的研究人员对个性化推荐技术的发展起到了积极的促进作用，提出了许多非常有效的改进算法来解决传统推荐算法中存在的不足。例如顾中华、郑楠等人分别以不同思路向传统相似度计算公式中加入了时间权重因子，解决了顾客偏好随时间变化的问题[11～14]；吴发青、刑春晓等人对用户的兴趣进行分析，分别提出了兴趣局部相似度计算方法及兴趣偏移处理方法[15,16]；张子科、周涛等人提出了应用用户—项目—标签的三元关系对传统推荐算法进行改进的新思路[17]；林霜梅、范波等人在用户行为参考及相似度优化方面也有效地改进了推荐算法[18～21]。

本文以个性化推荐技术在电子商务领域中的应用及个性化推荐系统为研究内容，以传统的基于用户的协同过滤推荐算法为研究对象，针对传统算法中评分矩阵过于稀疏等问题，提出了一种新颖的协同过滤改进算法，阐述了如何利用RFM模型合理地筛选用户信息，利用处理后的用户消费记录稠密用户—项目评分矩阵，并改进了传统相似度计算公式，以达到提高个性化推荐效果及预测准确度的目的。

2 协同过滤推荐算法的推荐过程

协同过滤算法的理论依据是基于这样一个事实：在日常生活中，所有人都不是孤立存在的，他们之间总会存在兴趣偏好上的相似性，且在一定的时间范围内是相对稳定的。每个用户都可以和在兴趣偏好或购买行为上与之相似或相同的其他用户组成一个用户类别，并且此用户更易于和同类别下的其他用户成为好朋友，故可以通过其好朋友的兴趣偏好对其自身的兴趣偏好进行预测。一般来说，此算法的推荐过程可分为用户数据表示 （user data representation）、最近邻查找（nearest neighbor query）、产生推荐集（recommended generate）3个环节。

用户对项目的评分可用一个m×n阶的用户—项目评分矩阵R（m，n）记录，其中，m、n分别表示系统内的总用户数及总项目数，每个元素代表系统内一个用户对一个项目的评分。

一般情况下评分矩阵中的评分值有两种形式：布尔数值和实数值评分区间形式。本文是在一个五级评分制下用户—项目评分矩阵中各项分值所对应的用户对项目的偏好情况。

3 改进的协同过滤推荐算法

在协同过滤算法理论基础上，提出了一种引入RFM模型并利用用户行为的个性化协同过滤推荐策略。

3.1 RFM模型

RFM模型是由美国人Arthur Hughes首先提出的，它是由用户的最近一次消费recency(R)、消费频率frequency(F)、消费金额monetary(M)3个参数对应的英文首字母组成的。最近一次消费用于衡量用户最近的一次消费行为产生时间距现在的时间长度大小。此要素定义标识的是一个时间范围，它与当前推荐算法的计算时间有关。某一条消费行为记录的消费时间是确定的，故R值会随着时间的推移逐渐变大。消费频率指用户在近一段时间内的消费次数。经常发生消费行为的用户，通常是对商家商品和服务满意度较高的用户，商家完全有理由相信此类用户的忠诚度及黏性比较高。增加用户对商家的消费次数意味着从竞争对手处获取市场占有率并赚取销售额，增加商品销量并提高企业收益。消费金额是对商家效益最直接的衡量指标，用户的消费金额越高，商家从其消费行为中的获益就越高，那么商家就越有理由相信该用户对自身效益做出了越大的贡献，该用户本身对商家也越忠诚。

3.2 用户—项目评分矩阵的改进

传统协同过滤算法中存在稀疏性问题，首先介绍评分矩阵的改进思想，随后定义了用户兴趣度概念，依据用户消费行为推测他们对商家商品的喜好程度，进而推测他们对未评分项目的预测分值，填充到初始矩阵中，降低矩阵稀疏程度。

3.2.1 评分矩阵的改进思想

协同过滤算法的一大不足即评分矩阵的稀疏性问题，此不足严重影响着整个算法的推荐质量，因此在实际运用中有必要对评分矩阵进行改进，即在不主动向用户索取信息、减轻用户负担的同时，达到提高系统推荐效果的目的。从另一方面说，每个用户在选购商品过程中，实际表现出了对该商品的喜好倾向，用户本身的购买行为标志着对该商品的喜好程度。借用此思想，可利用用户日常在商家中的消费行为来衡量其对各商品的喜好情况，进而预测他们可能在评分矩阵中的评分，并将预测评分填充到评分矩阵对应的商品项目上，进而稠密化评分矩阵，降低其稀疏度，完成评估矩阵的改进操作。

3.2.2 用户兴趣度定义

预测用户对未评分项目的评分，关键在于利用用户消费行为探索其对商品的喜好情况。为了准确规范地衡量用户对商品的喜好程度，同时便于理解，在此处引入用户兴趣度的概念。在阐述其定义及计算公式前，首先必须提出一种假设：每位用户对商家商品的喜欢程度，即兴趣度，可从该用户在一段时间内的历史消费记录反映出来。依据生活常识，若某用户在某时间段内购买某商品数量较多或购买次数较频繁，那么商家完全有理由相信该用户在此时间段更偏向于喜爱此商品，即该顾客对此商品的兴趣度较高。

依据商家掌握的用户消费行为，通过简单的数据提取即可获得一段时间范围内，每个用户对各项商品的购买次数及购买数量。如式（2）、式（3），可分别构造两个m×n阶矩阵A(m,n)和B(m,n)，前者表示用户—商品购买次数矩阵，即m个用户对n项商品的购买次数；后者表示用户—商品购买数量矩阵，即m个用户对n项商品的购买数量，其中，行数m表示系统总用户数，列数n表示系统中总商品数，矩阵中的元素Aij、Bij分别表示用户i对商品j的累计购买次数及累计购买数量。

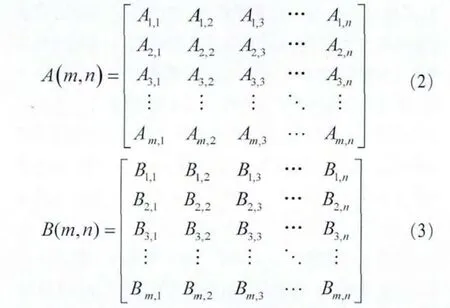
若采用五级制评分标准，以Cij表示用户i在此段时间内对商品j的兴趣度，则可定义为：

其中，Sij表示此段时间内用户i对商品j的单次平均购买数量；Tij表示系统内所有用户此段时间内单次平均购买数量，即商品j在所有用户下的总购买数量与总购买次数的比值；flag表示当前用户i对商品j的累计购买次数是否大于该商品的平均购买次数。它们的计算式分别如下：

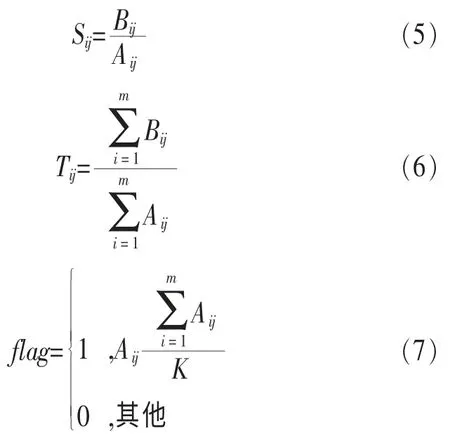
其中，K表示所有用户中购买过商品j的用户总数。

得到每个用户兴趣度后，便可开始评分矩阵的填充工作。若某用户对某商品的单次平均购买数量及累计购买次数两项指标均高于系统平均值，则说明该用户对此商品很感兴趣，对应评分矩阵项上可填充5分；若为其他3种情况，则在矩阵对应项上填充4分，即该用户比较喜欢该商品。

评分矩阵的改进操作中，有以下几点需要特殊说明。

·本算法改进中，填充操作仅针对评分矩阵中那些用户未做出评价的且根据用户消费行为，确实表现出喜好倾向的商品项目，即在矩阵中仅填充4分和5分，而未考虑商品项目的其他分值评分的填充，即用户不喜欢或感觉一般的商品。

·本文中的评分矩阵填充处理方法是有别于未评分项取平均分值等其他的矩阵填充方法的，因为本方法有效利用了商家容易获取到的用户消费行为数据，而且是用真实的用户相关数据稠密化评分矩阵，比纯粹地应用数学处理办法要好很多。

·以上定义的用户兴趣度计算针对的是用户在某时间段内的兴趣喜好，而非一成不变的，此时间段需要系统人员进行提前设置。也就是说系统人员想要分析哪个时间段内的用户兴趣，或想要以哪个时间段内的信息为数据源去完善评分矩阵，则设置哪个对应时间段跨度。这种预先设置时间段而后运行算法展开推荐的做法的好处是显而易见的，因为用户的兴趣喜好是随着时间偏移的，即他们的爱好可能会因时间的变化而不同。随着时间的推移，用户可能对某些商品的兴趣逐渐减弱，而在其他商品上产生新的兴趣点。因此，个性化推荐系统中的核心推荐算法部分很有必要适应这种用户的兴趣变化过程，否则做出的推荐更偏向于目标用户的原有兴趣点，而未迎合其新的兴趣点，导致推荐质量变差。

3.3 相似度计算公式的改进

相似度计算着眼于以下两点进行改进。

·所谓“个性化推荐”，其中的“推荐”二字，在普遍观念中当然是向用户推荐其可能感兴趣的、预测评分较高的商品，而不是判断有哪些商品用户可能不感兴趣、预测评分较低或没有可能购买，然后把此类商品推荐给用户，即使这样的推荐再准确，此行为本身也是毫无意义的，它已失去了推荐系统的本义，失去了推荐系统的初衷。故在进行目标用户与其他用户间的相似度计算，进而查找目标用户的最近邻居集合时，有必要把相似度分析侧重点从研究用户对所有商品喜好程度的相似性上向用户对感兴趣商品的喜好程度的相似性上进行转移，即计算出来的相似度应该是用户喜好商品间的相似度而非全部商品间的相似度。

·传统的协同过滤算法仅仅是在用户共同评分项目上考虑用户间对项目评分的相似性，通过此方面的匹配程度来衡量用户间的相似度，但却忽视了在实际评分矩阵中，矩阵本身评分项较少而导致稀疏度过高的情况下，用户间共同评分项数量大小的差异同样会对相似性的计算造成较大的偏差。

见表1中的评分矩阵，现要计算用户U3对商品项目D的预测评分值X，根据Pearson相似度计算式可计算出用户U3与用户U1、U2的相似度值均为1，但可明显看出用户U3与U1、U2的相似情况并不一样，即传统公式计算得出的相似度值并不准确。通过分析不难发现用户U3与用户U1在计算了3个商品评分后得出的相似度值，而用户U3与用户U2计算了1个商品的评分情况，由此可以看出，用户U3与用户U1相似度更高。

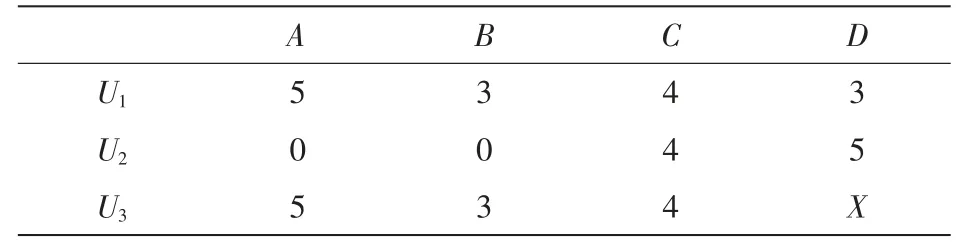
表1 共同喜好评分项目数量对相似度计算的影响

通过上例可发现，若在一个较小的项目集合中，即使两个用户间评分相似程度很高，那也不能确定他们的相似度很高。也就是说，传统相似度计算公式仅根据用户间的共同评分项来计算相似度，但未考虑共同评分项集合大小对相似度计算结果造成的影响。在此情况下，可考虑分析用户间的共同喜好商品的评分项与总评分项之间的大小权重关系，将此比例作为权重因子添加到原相似度公式中，对原有公式做出改进，如式（8）：

其中，用户a、b对项目i的评分利用Ra,i和Rb,i表示，用户a、b对项目的平均评分用Ra和Rb表示。用户a与b在共同喜好的评分项目集合用表示，用户a、b评价过的且为喜好的项目集合用和表示，而I则表示整个项目集合。本相似度计算式在传统的Pearson相似度计算公式上做了改进，它充分地考虑了系统向用户推荐喜好商品这一事实及共同喜好项目评分集合大小对相似度结果的影响。

值得注意的是，改进式中权重因子计算方法是两个用户间共同喜好评分项目的集合与共同评分集合求比值，即只关注用户评分中的4分、5分项，而不关注有哪些项目为1分、2分或是3分，此思想恰恰符合改进思路，到此即完成了对矩阵仅填充4分、5分评分值的问题解释。同时，在计算用户间相似度前，先对评分矩阵进行4分和5分值填充处理的好处在于，推荐算法不会因为评分矩阵中已评分项目过于稀少而影响最终权重因子计算的准确性。

4 改进算法的整体流程

基于协同过滤的个性化推荐算法流程如图1所示。

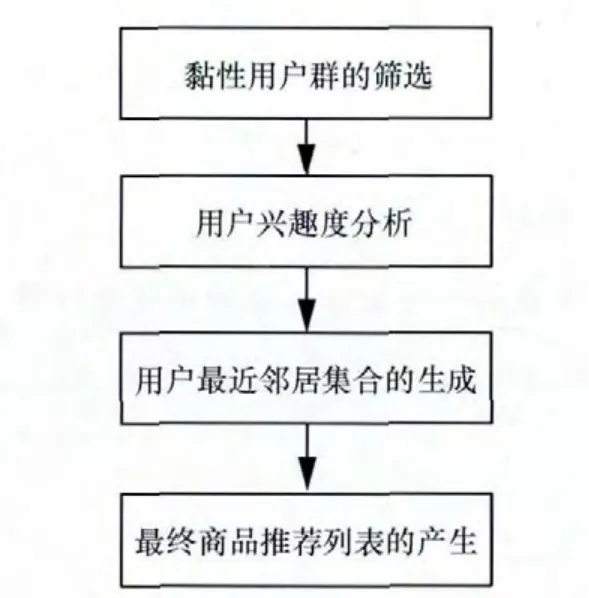
图1 改进算法的流程

具体实现步骤如下。

（1）黏性用户群的筛选过程，主要统计段时间内系统用户R、F、M值并根据设定后的参数对原用户群进行筛选处理，具体步骤如下。

·遍历系统内所有用户，根据他们的消费记录计算每个用户在分析时间段内的R、F、M值；

·将R值大于R参数设置值的用户过滤掉得过滤后集合A；

·将F值小于F参数设置值的用户过滤掉得过滤后集合B；

·将M值小于M参数设置值的用户过滤掉得过滤后集合C；

·按参数设置的大小及筛选意愿取集合A、B、C的交集或并集作为最终的黏性用户群。

（2）用户兴趣度分析

·遍历黏性用户群，统计每个用户对系统内各项商品的购买次数，求得用户—项目购买次数矩阵A；

·遍历黏性用户群，统计每个用户对系统内各项商品的累计购买数量，求得用户—项目累计购买数量矩阵B；

·依据式（5）、式（6）及式（7）计算每个用户对应的Sij、Tij及flag变量值并求得每个用户对各商品项的兴趣度；

·依据计算得到的兴趣度填充初始评分矩阵，生成填充后的新评分矩阵。

（3）目标用户最近邻居集合的生成

·遍历黏性用户群，依据填充后评分矩阵计算用户间的相似度，生成用户相似度矩阵；

·获取目标用户与其他用户间的相似度值，按递减顺序排序；

·截取相似度值排序Top N的用户作为目标用户的最近邻居集合。

（4）最终商品推荐列表的产生

·根据最近邻居集合，应用预测评分式，求得目标用户对未评分商品的预测分值并按递减顺序排序；

·将前N个预测评分较高的商品生成最终商品推荐列表。

5 实验设计与结果分析

为验证改进算法的可行性及效率，使用了如下的开发环境和开发工具进行实验。

（1）硬件配置

CPU：Intel Core i5-2520M 2.5 GHz；内存：4 GB；硬盘：250 GB。

（2）软件配置

操作系统：Windows7；编程语言：C#；开发平台：Visual Studio 2010；数据库：SQL Server 2008。

采用MAE（mean absolute error，均方绝对误差）作为改进算法推荐质量的度量标准，以数据堂提供的某科研小组收集的用户消费行为记录及商品项目评分数据为主实验数据集B，以MovieLens数据集为辅助实验数据集A，设计了多组对比实验并进行了实验结果分析。

实验中采用五重交叉验证技术，共在一个数据集上进行5次实验，最后取它们的实验结果平均值作为最终的算法验证结果。首先将原数据集合平均分为如图2所示的A、B、C、D、E 5份，再按4∶1的比例分出5种可能情况，将原始数据集中的4份，即80%的样本量作为训练集，用于产生推荐，另外的一份，即20%的样本量作为测试集，用于验证推荐算法质量。按此方法分割数据时，数据集A的训练集和测试集分别为80 000条和20 000条数据，而数据集B的训练集和测试集分别为9 600条和2 400条数据。五重交叉验证技术的优点在于一份数据集可进行5轮实验且在实验过程的数据应用中互不重复及覆盖，即将原数据信息进行了充分的利用。

5.1 改进后相似度计算式的有效性验证

针对改进后的相似度计算式，分别在两个数据集上应用余弦相似性、Pearson相似性和改进式运行传统协同过滤算法，通过推荐结果的MAE值大小比较相似度计算结果的准确程度，衡量3个相似度计算式自身的优劣性，判断改进式在相似度计算结果准确性上是否优于两个传统公式，同时找出两个传统公式中较优的一个，为实验方案设计选取比对公式做前期准备。实验中目标用户最近邻居数以10为间隔，逐渐从20增加到120，判断最近邻个数变化对MAE值的影响情况及3组结果的大小变化情况，实验结果如图3、图4所示。

通过图3、图4可得出如下结论：首先，就单条曲线来说，它的变化趋势是随着最近邻居数的增加，3条曲线均呈下降趋势，整个曲线前半部分下降速度较快，幅度较大，后半部分下降速度较慢并逐渐趋于平缓，当最近邻个数大于100时，曲线基本趋于稳定，MAE值基本不受邻居数变化的影响；其次，就3条曲线相互比对来说，改进式对应的曲线整体处于两种传统计算公式对应曲线的下方，说明使用它计算得到的MAE值更小，证明了改进式在预测效果上比两种传统公式效果更好，即改进式是可行有效的；第三，两种传统公式中Pearson相似度计算公式较优一些，故在接下来的实验中会采用Pearson公式与改进式的应用效果进行比较，以增强实验的可信度、说服力及严谨性。

5.2 改进后协同过滤推荐算法的有效性验证

利用数据集B，实验中采用Pearson公式与改进式的应用效果进行比较设计了3组实验。

5.2.1 RFM模型筛选用户群对推荐质量的影响

R、F、M 3个参数的设定标准可由筛选不同属性用户群的对象而定，对于不同的商家面向的用户来说，参数可能相差不大，也可能相差很大，因为不同属性的商品决定着不同消费时间差、消费频率及消费金额。故在筛选用户群前，需首先确定3个参数的合适值。

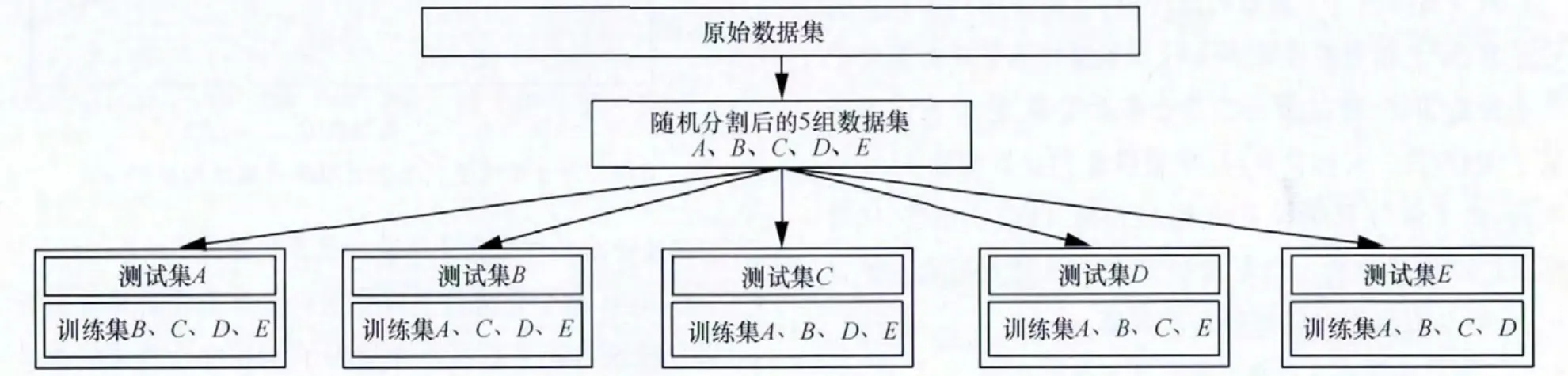
图2 原始数据集的处理过程

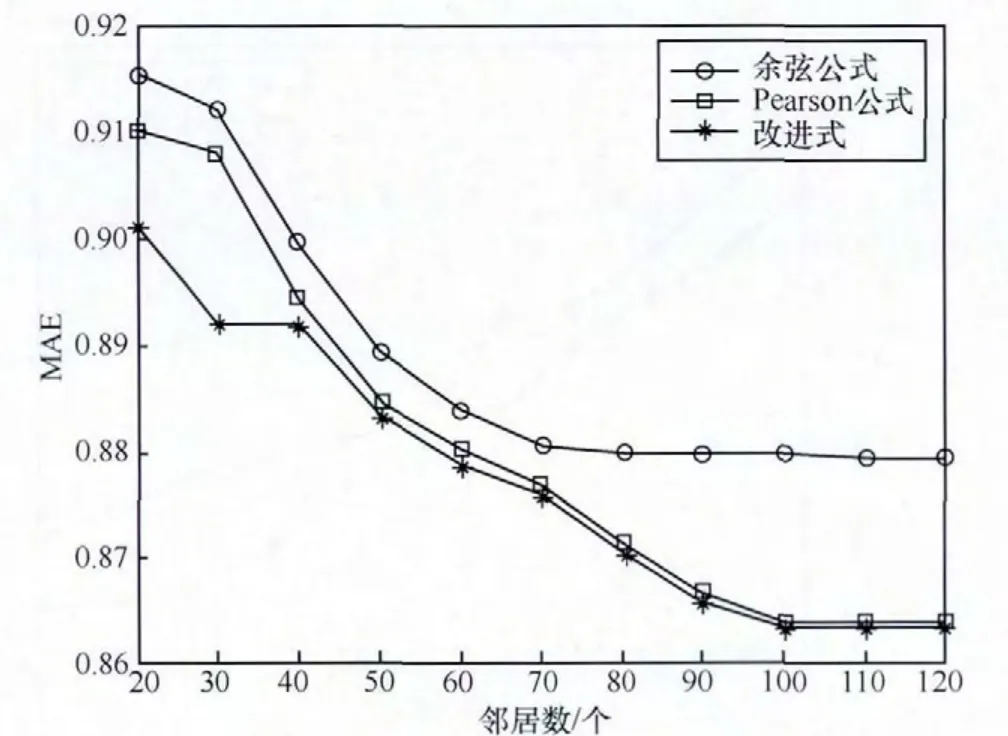
图3 在数据集A上的MAE结果对比

图4 在数据集B上的MAE结果对比

一般情况下，企业商家存储的用户消费行为数据初始格式为顾客ID、消费时间、消费金额等字段，利用此数据源即可完成对每个用户的筛选操作，进而生成RFM模型。

（1）最近一次消费（R）

本参数对应的数据形式为一个固定时间点，在进行用户筛选时，取当前的操作时间点与此时间点进行减法运算，并把运算结果赋给该参数。本参数的单位较为灵活，可根据操作人员需要自行设定，通常情况下按天计，若单位精确到分钟或粗略到年，在现实的应用场景中的实际意义就不大了。

（2）消费频率（F）

依据用户消费行为数据可直接计算得到其在某时间段内的消费次数（在本文处理中，若某用户在一天中存在着多次光顾和消费行为，按一个消费频率处理）。

（3）消费金额（M）

此参数计算简单，可直接计算得到用户在某时间段内的消费金额总和。

图5说明当3个参数较适中时，非黏性用户得到了有效过滤，应用相对黏性顾客进行相似度计算并在此集合中产生最近邻居，商品预测结果会准确得多，进而有效地降低了MAE值。实际设置时，尽量将R值设置的比AVG(R)大些，将F值与M值设置的比AVG(F)、AVG(M)小些，同时筛选后的用户集合人数尽量控制在原集合人数的一半以上，此时会取得相对较好的实验效果。

5.2.2 评分矩阵填充处理后对推荐质量的影响

以第5.2.1节中RFM模型筛选后的较优用户群为基础，分别在原评分矩阵及填充后评分矩阵上运行传统协同过滤算法，比较MAE值的大小，如图6所示。

从图6看出，对稀疏的评分矩阵进行填充处理后，所得的MAE值相比未填充处理时所得到的MAE值要低，尤其是在最近邻居个数相对较少时，MAE值下降幅度较大，说明当最近邻居较少时填充操作可明显提高推荐质量。之后随着最近邻居数的增加，MAE值仍然逐渐变小，但变化速率开始减慢，最终曲线趋于平缓，填充矩阵后的MAE值曲线基本处于原矩阵的MAE曲线下方。故可以说明应用用户消费行为及兴趣度概念对评分矩阵进行填充处理的方法是有效的。

图5 RFM模型筛选用户群对推荐质量的影响对比（R=95天、F=5次、M=300元）

图6 评分矩阵填充处理后对推荐质量的影响对比

5.2.3 改进后的相似度计算式对推荐质量的影响

在RFM模型筛选后的较优用户群及填充后评分矩阵上运行传统协同过滤算法和加入了相似度改进式的改进算法，比较MAE值的大小，如图7所示。

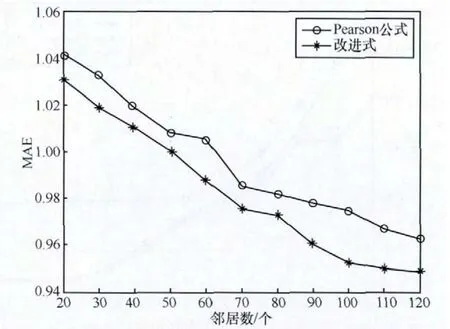
图7 改进后的相似度计算式对推荐质量的影响对比

从图7可看出，引入权重因子后，在两个用户间的共同喜好商品上计算相似度，求得的MAE值要比应用传统Pearson公式时的MAE值要低，虽然随着最近邻居数的增加，MAE值减小的速率逐渐变慢，推荐质量的改善程度有所下降，曲线逐渐趋于平缓，但其依然优于应用传统公式时的推荐效果，前者对应的曲线各部分明显处于后者下方，证明了改进式的积极意义。

6 结束语

本文以提高推荐准确度为目标，在传统的基于用户的协同过滤算法上进行了改进，提出了一种引入RFM模型并利用用户购物行为进行相似度计算的新型推荐算法。本算法与传统算法相比，其优势主要体现在：新算法中引入RFM模型对原用户群进行了多条件筛选，使推荐数据源更加准确高效；改进算法中利用顾客历史消费记录对原评估矩阵进行填充处理，提高了评分矩阵的稠密度；对传统的Pearson相似度计算公式进行改进，使目标用户的相似邻居查找更加准确；最后，将改进算法应用于一套具有个性化商品推荐功能的实用性推荐系统中，验证了该推荐算法的实用性、高效性和准确性。

1 刘建国,周涛,汪秉弘.个性化推荐系统的研究进展.自然科学进展,2009,19(1):2～7 Liu J G,Zhou T,Wang B H.Research progress of personalized recommendation system.Progress in Natural Science,2009,19(1):2～7

2 蒋盛益,李霞.数据挖掘原理与实践.北京:电子工业出版社,2011 Jiang S Y,Li X.Principle and Practice of Data Mining.Beijing:Publishing House of Electronics Industry,2011

3 Adomavicius G,Tuzhilin A.Toward the next generation of recommender systems:a survey of the state-of-the-art and possible extensions.IEEE Transactions on Knowledge and Data Engineering,2005,17(6):734～749

4 Ahn H J.A new similarity measure for collaborative filtering to alleviate the new user cold-starting problem.Information Sciences,2008,178(1):37～51

5 Lemime D,Maclachlan A.Slope one predictors for online rating-based collaborative filtering.Proceedings of SIAM Data Mining Conference,Newport Beach,California,USA，2005

6 Huang Z,Chen H,Zeng D.Analyzing consumer-product graphs:empirical findings and applications in recommender systems.Management Science,2007,53(7):1146～1164

7 Zhang F,Chang H Y.A collaborative filtering algorithm embedded bp network to ameliborate sparsity issue.Proceedings of 2005 International Conference on Machine Learning and Cybernetics,Guangzhou,China,2005:1839～1844

8 Deshpande M,Karypic G.Item-based top-n recommendation algorithms.ACM Transactions on Information Systems,2004,28(1):143～177

9 Kim H N.Collaborative filtering based on collaborative tagging for enhancing the quality of recommendation.Information Processing and Management,2009(8):368～379

10 Das A,Datar M,Garg A.Google news personalization:scalable oline collaborative filtering.Proceedings of the 16th International Conference on World Wide Web,Banff Alberta,Canada,2007

11 顾申华.结合奇异值分解和时间权重的协同过滤算法.计算机应用与软件,2010,27(6):256～259 Gu S H.Collaborative filtering algorithm combining singular value decomposition and time weight.Computer Applications and Software,2010,27(6):256～259

12 Zheng N,Li Q D.A recommender system based on tag and time information for social tagging systems.Expert Systems with Applications,2011(38):4575～4587

13 丛晓琪,杨怀珍,刘枚莲.基于时间加权的协同过滤算法研究.计算机应用与软件,2009，26(8):120～140 Cong X Q,Yang H Z,Liu M L.On collaborative filtering algorithm based on time weight.Computer Applications and Software,2009，26(8):120～140

14 彭德巍,胡斌.一种基于用户特征和时间的协同过滤算法.武汉理工大学学报,2009，31(3)：24～28 Peng D W,Hu B.A collaborative filtering recommendation based on user characteristics and time weight.Journal of Wuhan University of Technology,2009，31(3)：24～28

15 吴发青,贺樑，夏薇薇.一种基于用户兴趣局部相似性的推荐算法.计算机应用,2008,28(8):1981～1985 Wu F Q,He L,Xia W W.A recommendation algorithm based on users’partial similarity.Computer Applications,2008,28(8):1981～1985

16 刑春晓,高凤荣,战思南.适应用户兴趣变化的协同过滤推荐算法.计算机研究与发展,2007,44(2):196～231 Xing X C,Gao F R,Zhan S N.A collaborative filtering recommendation algorithm incorporated with user interest change.Journal of Computer Research and Development,2007,44(2):196～231

17 Zhang Z K,Zhou T.Personalized recommendation via integrated diffusion on user-item-tag tripartite graphs.Physica A：Statistical Mechanics and its Applications,2010,389(1):179～186

18 林霜梅,汪更生,陈弈秋.个性化推荐系统中的用户建模及特征选择.计算机工程,2007,33(17):196～198Lin S M,Wang G S,Chen Y Q.User modeling and feature selection in personalized recommending system.Computer Engineering,2007,33(17):196～198

19 赵银春,付关友,朱征宇.基于Web浏览内容和行为相结合的用户兴趣挖掘.计算机工程,2005,31(12):93～94 Zhao Y C,Fu G Y,Zhu Z Y.User interest mining of combining web content and behavior analysis.Computer Engineering,2005,31(12):93～94

20 范波,程久军.用户间多相似度协同过滤推荐算法.计算机科学,2012,19(39):23～26 Fan B,Cheng J J.Collaborative filtering recommendation algorithm based on user’s multi-similarity.Computer Science,2012,19(39):23～26

21 徐翔,王煦法.协同过滤算法中的相似度优化方法.计算机工程,2010,36(6):52～54 Xu X,Wang X F.Optimization method of similarity degree in collaborativefilteralgorithm.ComputerEngineering,2010,36(6):52～54

22 Konstan H.Evaluating collaborative filtering recommender system.ACM Transactions on Information Systems,2004,22(1):5～53

23 李春,朱珍民,高晓芳.基于邻居决策的协同过滤推荐算法.计算机工程,2010,36(13):34～36 Li C,Zhu Z M,Gao X F.Collaborative filtering recommendation algorithm based on neighbor decision-making.Computer Engineering,2010,36(13):34～36

24 邓爱林,朱扬勇,施伯乐.基于项目评分预测的协同过滤推荐算法.软件学报,2003,14(9):1621～1628 Deng A L,Zhu Y Y,Shi B L.A collaborative filtering recommendation algorithm based on item rating prediction.Journal of Software,2003,14(9):1621～1628