相关向量机软件可靠性建模中失效数据选择

1 引言

软件可靠性模型是指为预测软件可靠性，利用己有失效数据，根据对软件失效行为的假设，采用一定数学方法建立软件可靠模型的过程[1]。近年来，研究者提出了许多软件可靠性模型，这些模型都是基于一些对软件的开发环境和使用环境的关键假设，利用测试获得的软件失效信息，对软件系统的失效过程进行建模，评估软件系统的可靠性，预测软件实际工作时的现场行为[2]。软件可靠性是最重要的可信性属性之一，而软件可靠性建模是目前提高软件可靠性水平主要工具之一。软件可靠性模型多是基于一些对软件的开发环境和使用环境的关键假设，利用测试获得的软件失效信息，对软件系统的失效过程进行建模，评估软件系统的可靠性水平，预测软件实际工作时的现场行为。随机过程模型是软件可靠性建模研究中最广泛使用的，也是实际项目中应用最广泛的一类，目前这类模型的绝大部分研究工作集中于模型的统一、对非齐次泊松过程类（non-homogeneous Poisson process，NHPP）等模型的改进、可靠性成本模型等[3～8]，模型改进的出发点是提出更加合理的假设以提高模型预测精度，如考虑测试环境与实际运行环境的差别、考虑故障的相关性、不完美调试以及测试者学习能力、测试效用函数、测试工作量与覆盖率等。此外，也有学者提出采用马尔可夫更新过程、广义Pareto分析、排队论模型、顺序统计量模型、多维随机过程等来描述软件失效过程，取得了很多不错的研究成果[9～11]。接着，人们尝试利用更多更复杂的数学方法对软件失效行为进行建模及分析，如人工神经网络、未确知理论、混沌理论、时间序列、模糊数学理论、遗传编程、强化学习[12～15]等，相比随机过程模型，这些方法可以取得更好的预测性能或拟合效果，但在实际软件系统可靠性评估的应用还较为少见。最近，研究者开始考虑核函数方法在软件可靠性建模方面的研究，最主要的包括支持向量机（support vector machines,SVM）、相关向量机（relevance vector machine，RVM）等方法的应用，核函数方法一般对软件失效时刻与在它之前的发生m个失效时刻数据之间的对应关系进行建模。Tian等把SVM引入软件可靠性建模中[16]，Xing等[17]、Yang等[18]、Yuan等[19]、Park等[20]对SVM用于可靠性建模进行了适当的改进。楼俊钢等人使用RVM等核函数技术在软件可靠性建模方面做了一些研究工作[21,22]。与其他方法相比，SVM、RVM等基于核函数模型具有自适应能力和学习功能，通过归纳学习和训练，能发现数据输入与输出之间的关系，经过自适应调整求取问题的解，适用于系统开发环境较复杂，对问题的机理不能用数学模型表示的系统，对大量原始数据的处理往往表现出极大的灵活性和自适应性，容错和抗干扰能力较强，在软件可靠性建模问题上也得到了较好地应用，在模型适用性以及评估预测能力上均有较好的表现，是目前软件可靠性模型研究中较为重要的一个突破口。笔者在使用核函数理论进行软件可靠性预测的前期研究中，发现用于建模的软件失效数据数量的改变对模型的预测性能和适用性有较大影响[22]。然而目前的研究工作中，还很少有专门针对软件失效数据数量选取的工作，本文应用Mann-Kendall及配对T-检验等统计方法在5个常用软件失效数据集上对基于相关向量机的软件可靠性预测模型中m值选取问题进行研究。

2 基于相关向量机的软件可靠性建模

假设已发生的软件失效时间为t1,t2,…,tn，基于相关向量机的软件可靠性预测问题可以描述为：从已知失效时间间隔数据序列预测未知的软件失效时间间隔数据ti+d，使用核函数对软件失效时间与在它之前的m个失效时间数据建模，以此捕捉失效时间内在的依赖关系，一般地，令tl=f(tl-m,tl-m+1,…,tl-1)，则tl服从固定但未知的条件分布函数F(tl|tl-m,tl-m+1,…,tl-1)。假设用于学习的失效时间序列为t1,t2,…,tk(k>m)，则在t1,t2,…,tk已知条件下对tk+1进行预测变为：已知k-m个观测(T1,tm+1),(T2,tm+2),…,(Tk-m,tk)和第k-m+1个输入Tk-m+1的情况下，估计第k-m+1个输出值，其中Ti表示m维向量[ti,ti+1,…,tm+i]。把[t2,ti+1,…]作为输入，则可以预测，同理可以预测得到对可以获得的部分系统输出数据即失效数据进行分析，将其蕴涵的系统失效特征用核函数进行学习并表达出来，构造软件故障过程的等价系统，从而完成对软件系统失效行为的刻画，并依据所建模型完成对系统未来失效行为的预测。对基于相关向量机的软件可靠性模型的详细描述可参见参考文献[13,14]。

预测的具体实现步骤如图1所示。具体介绍如下。

2.1 使用的数据集和性能比较标准

采用10个来自不同类型软件的失效数据集[23]对m不同时模型预测性能进行实验分析，见表1，在实验过程中，取所有数据集的前2/3作为学习数据，对后面1/3数据进行预测后与真实数据进行比较。

图1 基于相关向量软件可靠性预测的基本步骤

使用软件可靠性预测模型性能分析中最常用的指标平均相对预测误差 (average relative prediction error，AE)[23]对模型性能进行评价，AE的值越小说明模型的预测能力越强，计算式为其中，n表示失效数据集总共记录的失效次数，k表示用于核函数学习的失效次数表示第i次失效时间估计值而ti失效时间实测值。

2.2 核函数参数选取

前期工作[22]表明模型中选用高斯核函数K(xi,xj)=exp时可以取得最好预测效果，r＞0是高斯核函数的带宽参数。核函数参数选取是一个最优化问题，采用网格搜索法进行核函数参数选择，令r∈[r1,r2]，设置变化步长为rs，选取其中预测效果最好的值作为模型参数。在数据集1～数据集5上采用不同的r值进行的实验研究结果如图2所示，其中，r1,r2,rs的取值分别为0、12和0.1，其余取值如下：m=8,αi(i=1,2,3,…,m)的初始值均为0.5，σ2的初始值为1。从图2中可以看出，r的取值对模型预测性能有较大的影响，本文实验中对5个数据集上r的取值见表2。

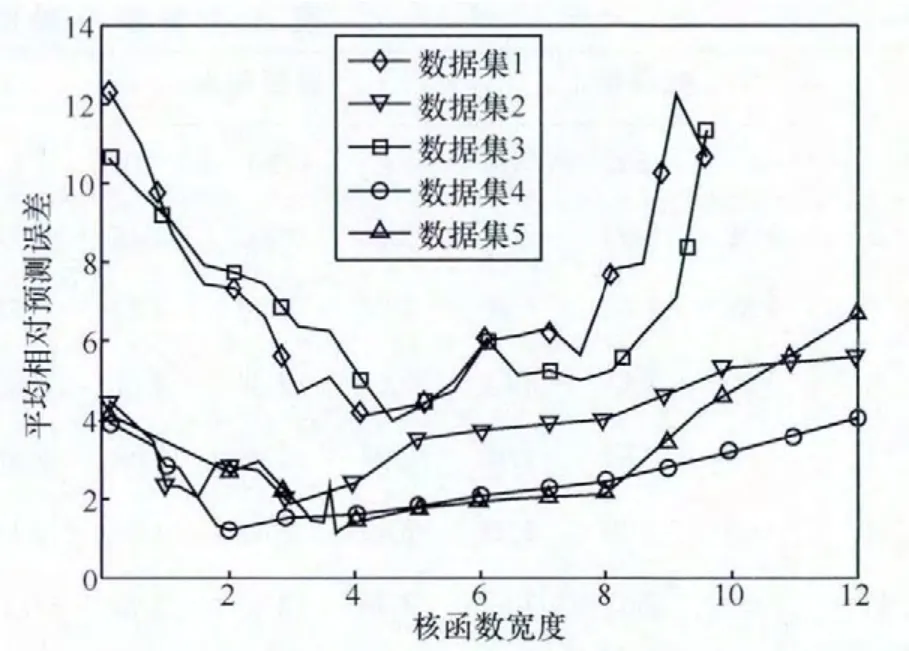
图2 10个数据集上r值不同时模型预测性能变化曲线

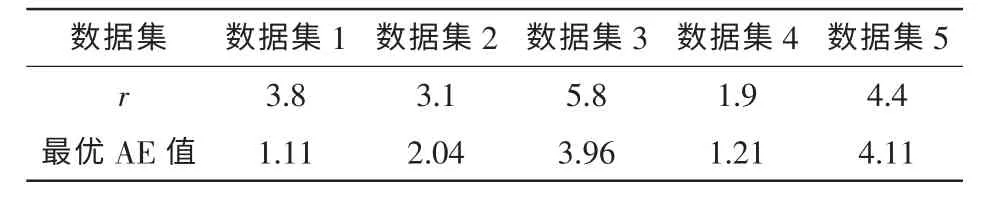
表2 模型性能最佳时的r值

3 实验分析与比较

3.1 Mann-Kendall检验

假定x1,x2,…,xn为m值不同时的AE值序列变量，n为序列的长度。检验统计值可由计算[25]，如果检验统计值S的值接近于0，则序列数据中不存在趋势；如果检验统计值S的绝对值较大，则可以断定数据中存在趋势。定义检验统计值：在给定的α置信水平上，时拒绝原假设。即在α置信水平上，m取值不同时的AE值序列数据存在明显的上升或下降趋势，其中Var(S)=

3.2 检验结果及趋势分析

表3列出了在m取值分别为6,7,…,30情况下各个数据集上模型的预测AE值，图3显示了其变化趋势。模型中σ2的初始值为1，αi(i=1,2,3,…,m)的初始值均为0.5，r的取值为1、10以及表2中的值。从表3中可以看出，随着m值的不同，模型预测性能也有极大差异。例如，在使用数据集1、r=3.8时，AE的值在0.87(m=9)与2.42(m=28)之间浮动；使用数据集4、r=1时，AE的值在1.68(m=13)与6.15(m=25)之间浮动。

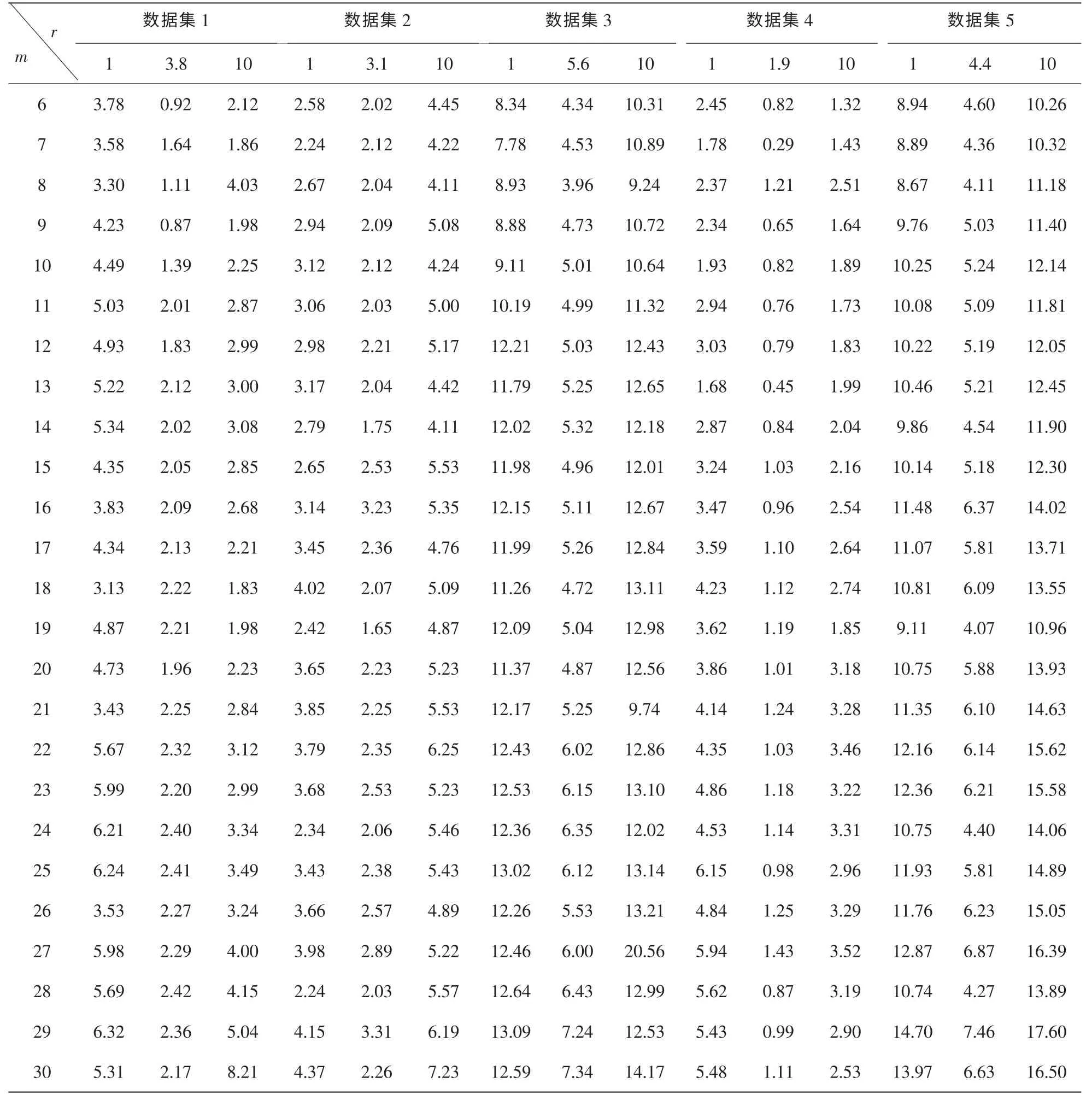
表3 数据集1～数据集5上m值不同时模型单步预测值

表4中给出了各数据集上m值变化时的Z统计量及置信区间为95%（α=0.5,Z1-α/2=1.96）时的变化趋势分析。从表4中可以看出，m值增加时，在各数据集的AE值均存在上升趋势，说明随着m的增加，模型的预测性能存在下降的趋势。合理的解释是，最近的失效数据更能反映失效过程中的最新特性，早期失效数据对预测未来短期失效行为作用较小，现时失效时间数据能比很久之前观测的失效时间数据更好地用于预测未来。

3.3 配对T检验

本节将设计随机化实验，采用配对T检验的方法找出10个数据集上模型预测能力相对较好的m值。配对T检验的过程，是对两个同质的样本分别接受两种不同的处理，判断不同的处理是否有差别，实验中，将m值作为处理，判断其不同时模型预测能力是否有差别。令{X}、{Y}为m值取值集合，定义集合运算>，{X}＞{Y}表示采用集合X中的数值比采用集合Y中数值具有更好的预测性能。实验中，把m值分成5组：

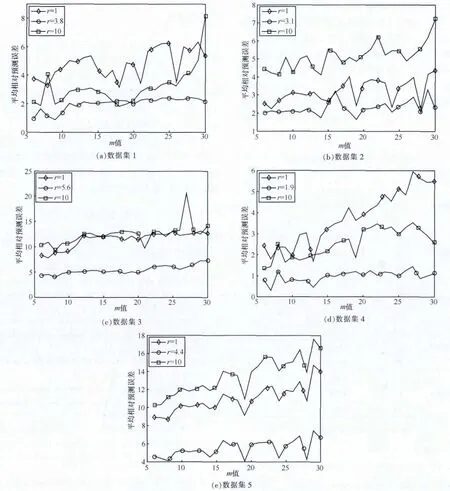
图3 各数据集上m值不同时模型预测值变化趋势

{A}={6,7,8,9,10}

{B}={11,12,13,14,15}

{C}={16,17,18,19,20}

{D}={21,22,23,24,25}

{E}={26,27,28,29,30}，

配对10次：

{A}→{B},{A}→{C},{A}→{D},{A}→{E}

{B}→{C},{B}→{D},{B}→{E}

{C}→{D},{C}→{E}

{D}→{E}。

在H0:μ1-μ2≥D0假设下，小样本情况下配对检验可用统计量表示[18]，其中n表示样本数量，di第i个配对样本数据的差值di=xi-yi，i=1,2,…,n,表示配对样本数据差值的平均值表示配对样本数据差值的总体标准差，Sd表示配对样本数据差值的标准差。表5中给出了D0=0的检验结果，Sig.表示significance，在置信度α取值为95%的双侧检验情况下，如果0.01＜Sig.＜0.05则表示差异显著，如果Sig.＜0.01表示差异极显著，这两种情况下，拒绝H0假设。从表中可以看出，{A}＞{C}、{A}＞{D}、{A}＞{E}、{B}＞{C}、{C}＞{D}、{C}＞{E}的结论均极显著，因此可以得出结论：使用基于RVM的软件可靠性模型时，在区间[6,30]中，m∈{6,7,8,9,10}为最佳取值。

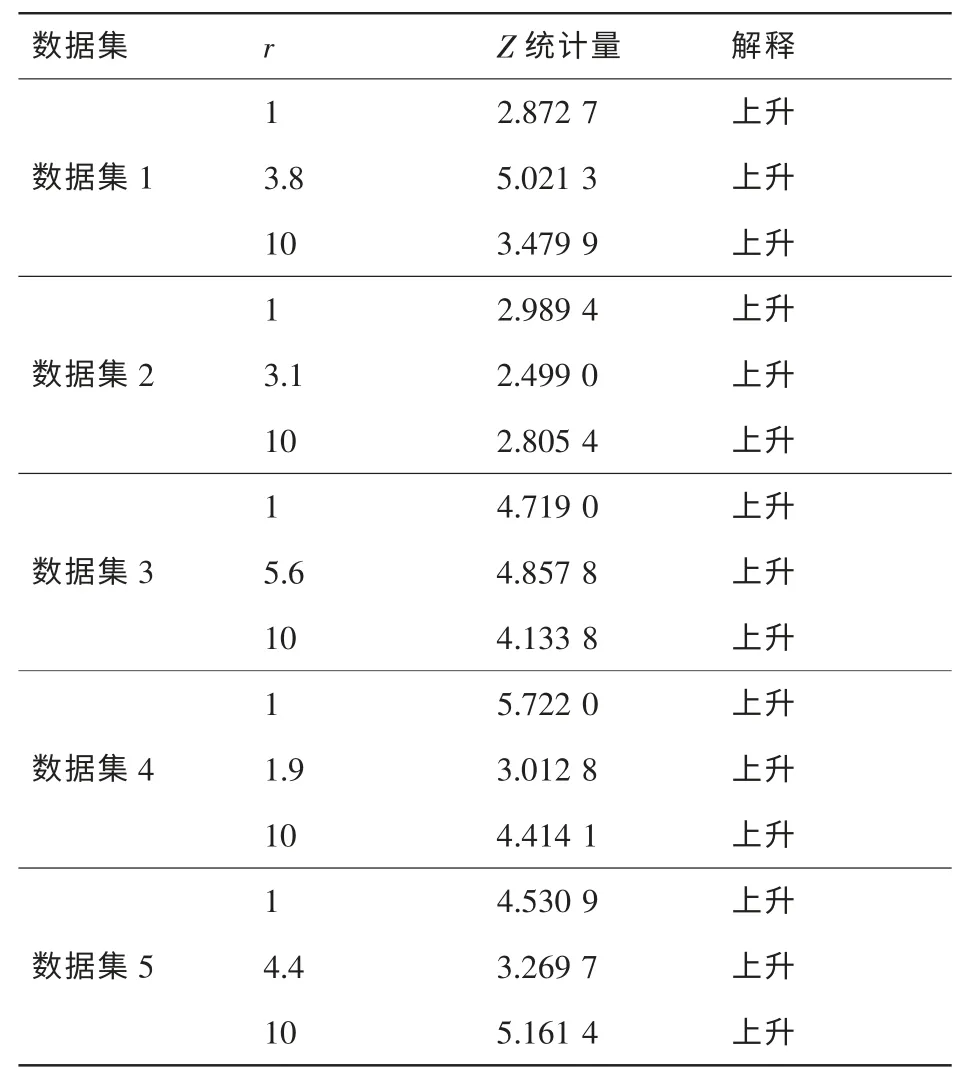
表4 各数据集上的AE值趋势检验

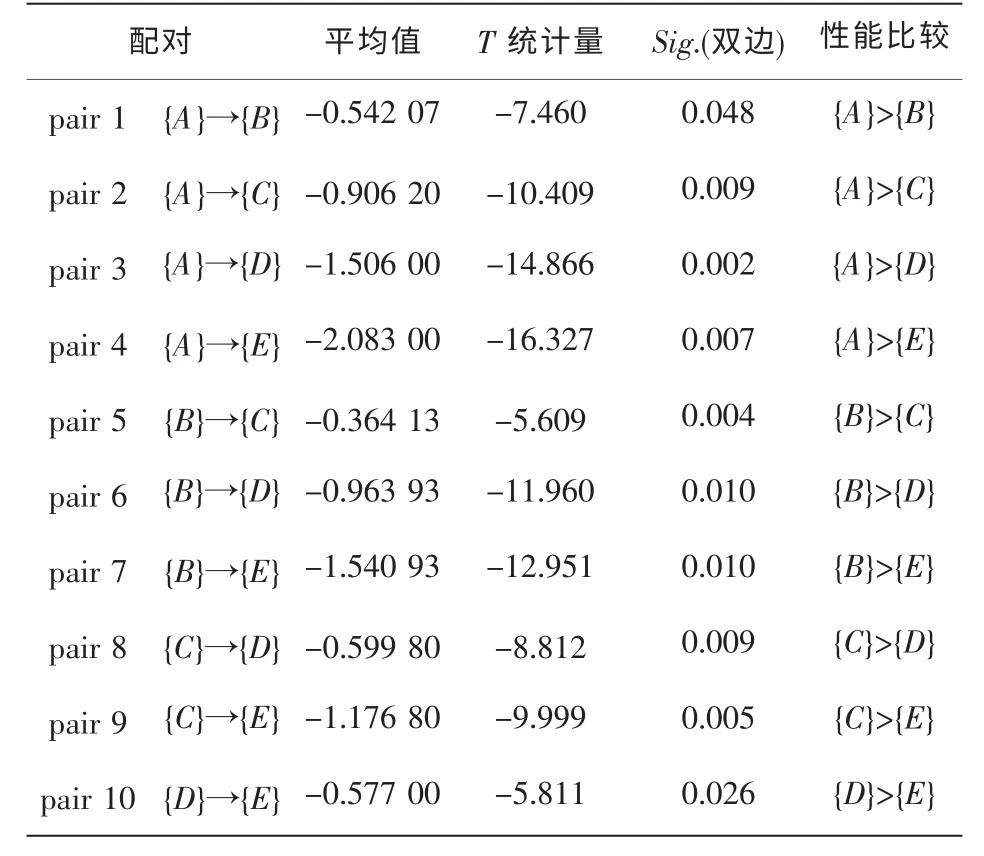
表5 配对T-检验分析结果

4 结束语

基于相关向量机理论，对软件失效时间数据与在其之前发生的m个失效时间数据进行建模，对10个数据集上用于建模的失效数据数量进行实验研究。首先，通过Mann-Kendall检验发现，m值变大时，模型预测性能存在下降趋势，然后采用配对T检验发现，在10个数据集上，m∈{6,7,8,9,10}时，模型具有最好的预测性能。

进一步工作包括以下内容：采用模糊遗传算法、粒子群算法或者模拟退火算法等优化技术对核函数参数的自动赋值算法进行研究；适合于软件可靠性建模的核函数选择及构建，进一步提高模型预测性能。

1 IEEE Std 1633-2008.IEEE Recommended Practice on Software Reliability,2008

2 Inoue S,Yamada S.Generalized discrete software reliability modeling with effect of program size.IEEE Transactions on Systems,Man and Cybernetics,Part A:Systems and Humans,2007,37(2):170～179

3 Liu M X,Miao L,Zhang D Q.Two stage cost sensitive learning for software defect prediction.IEEE Transactions on Reliability,2014,63(2):676～686

4 李海峰,王栓奇,刘畅等.考虑测试工作量与覆盖率的软件可靠性模型.软件学报,2013,24(4):749～760 Li H F,Wang S Q,Liu C,et al.Software reliability model considering both testing effort and testing coverage.Journal of Software,2013,24(4):749～760

5 Peng W,Huang H Z,Xie M,et al.A Bayesian approach for system reliability analysis with multilevel pass fail,lifetime and degradation data sets.IEEE Transactions on Reliability,2013,62(3):689～699

6 陆文,徐锋,吕建.一种开放环境下的软件可靠性评估方法.计算机学报,2010,33(3):452～462 Lu W,Xu F,Lv J.An approach of software reliability evaluation in the open environment.Chinese Journal of Computers,2010,33(3):452～462

7 Sun Z B,Song Q B,Zhu X Y.Using coding based ensemble learning to improve software defect prediction.IEEE Transactions on Systems,Man,Cybernetics,2012,42(6):1806～1817

8 Chatzis S,Andreou A.Maximum entropy discrimination poisson regression for software reliability modeling.IEEE Transactions on Neural Networks and Learning,2015,has been accepted by inclusion in a future issue

9 谢景燕,安金霞,朱纪洪.考虑不完美排错情况的NHPP类软件可靠性增长模型.软件学报,2010,21(5):942～949 Xie J Y,An J X,Zhu J H.NHPP software reliability growth model considering imperfect debugging.Journal of Software,2010,21(5):942～949

10 陆文,徐锋,吕建.一种开放环境下的软件可靠性评估方法.计算机学报,2010,33(3):452～462 Lu W,Xu F,Lv J.An Approach of Software Reliability Evaluation in the Open Environment.Chinese Journal of Computers,2010,33(3):452～462

11 Schneidewind N,Hinchey M.A complexity reliability model.Proceedings of 20th International Symposium on Software Reliability Engineering,Mysuru,India,2009:1～10

12 Cotroneo D,Pietrantuono R,Russo S.Combining operational and debug testing for improving reliability.IEEE Transactions on Reliability,2013,62(2):408～423

13 Liu M X,Miao L,Zhang D Q.Two stage cost sensitive learning for software defect prediction.IEEE Transactions on Reliability,2014,63(2):676～686

14 Wayne M,Modarres M.A bayesian model for complex system reliability growth under arbitrary corrective actions.IEEE Transactions on Reliability,2015,64(1):206～220

15 Li X N,Mabu S,Hirasawa K.A novel graph based estimation of the distribution algorithm and its extension using reinforcement learning.IEEE Transactions on Evolutionary Computation,2014,18(1):98～113

16 Tian L,Noore A.Dynamic software reliability prediction:an approach based on support vector machines.International Journal of Reliability,Quality and Safety Engineering,2005,12(4):309～321

17 Xing F,Guo P,Lyu M R.A novel method for early software quality prediction based on support vector machines.Proceedings of International Symposium on Software Reliability Engineering(ISSRE’05),Chicago,Illinois,USA,2005:213～222

18 Yang B,Li X.A study on software reliability prediction based on support vector machines.Proceedings of IEEE International Conference on Industrial Engineering and Engineering Management,Singapore,2007:1176～1180

19 Yuan F Q,UDAY K,MISRA K B.Complex system reliability evaluation using support vector machine for incomplete data-set.International Journal of Performability Engineering,2011,7(3):32～42

20 Park J,Lee N,Baik J.On the long-term predictive capability of data-driven software reliability model:an empirical evaluation.Proceedings of 25th International Symposium on Software Reliability Engineering,Naples,2014:45～54

21 楼俊钢,蒋云良,申情等.软件可靠性预测中不同核函数的预测能力评估.计算机学报,2013,33(6):1303～1311 Lou J G,Jiang Y L,Shen Q,et al.Evaluating the prediction performance of different kernel functions in kernel based software reliability models.Chinese Journal of Computers,2013,36(6):1303～1311

22 Lou J G,Jiang J H，Shuai C Y.A study on software reliability prediction based on transduction inference.Proceedings of IEEE 19th Asian Test Symposium,Los Alamitos:IEEE Computer Society,Shanghai,China,2010:77～80

23 Ohba M.Software reliability analysis models.IBM Journal of Research and Development,1984,28(4):428～443

24 Kendall M G.A new measure of rank correlation.Biometrical,1938,30(2):81～93

25 Douglas C D.Design and Analysis of Experiments,6th Edition.New York:John Wiley & Sons.Inc,2007