实验中测量不确定度问题的研究

李艳梅，范 羽

(肇庆学院 电子信息与机电工程学院，广东 肇庆 526061)

实验中测量不确定度问题的研究

李艳梅，范 羽

(肇庆学院 电子信息与机电工程学院，广东 肇庆 526061)

文中介绍了测量不确定度概念从产生到评定方法取得国际化统一的发展历程，给出了有关测量不确定度的国内外技术规范，对比给出了不确定度、误差、准确度和精确度几个概念的定义，并简要分析了它们之间的关系。在此基础上，给出了不确定度的A类和B类两种评定方法，并重点归纳了A类评定方法的具体步骤。最后，总结了不确定度的六个具体评定步骤：建立数学评定模型、求最佳估计值、标准不确定度分量的计算、标准不确定度的合成、扩展不确定度的求解、提供最终不确定度报告。

测量不确定度；评定；方法；实验

1 测量不确定度的发展历程

在高校实验教学和科研工作中，测量是一项重要的、必不可少的基础性工作。测量的品质与实验和研究的成败息息相关。测量不确定度是用来描述由于测量误差的存在而导致被测量值不能被准确测量的程度，比测量误差更具有可操作性和通用性[1]。测量不确定度概念清楚，评定方法及合成方法统一，通过有限次测量以及经验、资料等信息实现可操作性，是经典误差理论的发展和完善[2]。

在测量中，给出相应的不确定度，既便于使用者评定其可靠性，又增强了测量结果之间的可比性。

测量不确定度最早由美国国家标准局(NBS)于1963年提出。20世纪70年代，NBS对不确定的定量表示进行了深入研究，不确定度在测量行业被广泛引用；但其表示方法却不尽相同，影响了不确定度的推广应用，因此，对不确定度的表征方式、方法在国际上进行统一提出了迫切需求。

1980年，在国际计量委员会(CIPM)和NBS的联合推动和组织下，国际计量局(BIPM)对32个国家和5个国际组织就不确定度的统一表示问题征求意见，并对收集到的21个国家的反馈意见进行了研究，起草了一份建议书，即INC-1(1980)。该协议书推荐了统一的不确定度表示原则。

1981年，CIPM 在INC-1(1980)的基础上，正式发布了CI-1981文件。该文件于1986年得到再次确认，并被新版本CI-1986替代。至此，不确定度的定量表示方法得到统一。该方法不仅应用于计量部门，在众多使用测量结果的领域也得到了大力推广。

为了使CI-1986能在国际范围内得以推广应用，国际标准化组织(ISO)于1993年发布了《测量不确定度表示与指南》(即GUM)。该指南采用通行的理念和方法，使不同的测量技术主体可以用统一的标准对测量结果及其质量进行评判和比对。我国发布的《不确定度评定与表示》(JJF 1059—1999)，原则上等同采用GUM的基本内容，广泛应用于科学研究、工程技术等领域的测量结果的处理和表示。

2 测量不确定度与误差、准确度和精密度之间的比较

2.1 不确定度产生的因素

不确定度是一个复合性概念，产生不确定的因素有随机效应和系统效应，两者辩证统一，在不同的情况下，可以互相转化。不能单纯地将不确定度分为随机不确定度和系统不确定度，而应将不确定度分为“系统效应引起的不确定度分量”和“随机效应引起的不确定度分量”。系统效应引起的不确定度主要来源于仪器本身的缺陷、实验方法的不完善、环境条件对仪器的影响、实验者不良的实验习惯等因素。系统效应引起的不确定度的特点是测量值总是有规律地朝一方偏离，消除的方法主要包括改进测量仪器、校正仪器、对实验理论进行完善、纠正实验者不良习惯等。随机效应引起的不确定度主要来源于一些偶然的因素对实验的干扰，使测量结果产生偏差，其特点是无方向性、离散性，消除方法主要是对同一测量进行多次重复测量。

相对于由系统效应引起的不确定度，随机效应引起的不确定度更易处理和定量分析：评定随机效应引起的不确定度具有相对统一的方法；而系统效应引起的不确定度则要具体问题具体分析，需要相关实验者积累丰富的经验，没有通用的评定方法。不确定度产生的因素如图1所示。

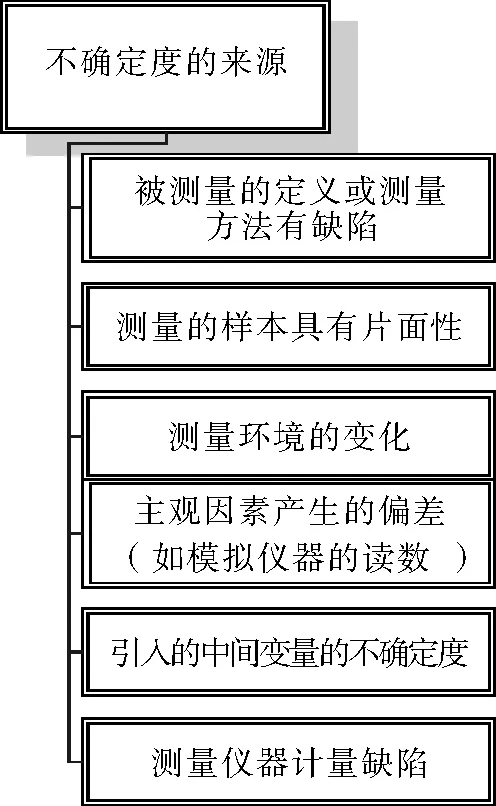
图1 测量不确定度的来源

2.2 几个概念的比较

测量不确定度与测量误差是迥然不同的两个概念，两者之间不能画等号。 “JJF 1059—1999”中将测量不确定度定义为：表征合理的赋予被测量之值的分散性，与测量结果相联系的参数。不确定度越小，测量结果越接近被测量的真值，测量结果品质越高；反之，测量结果的品质越低。由于产生不确定因素的多元化，测量不确定度最终结果由若干分量组成：其中一些分量采用实验标准差表示，可用测量列结果的统计分布估算，即A类不确定度评定方法；另一些分量可用源于经验等信息的假定概率分布进行推算，通常称为B类评定方法。

在实验不确定度概念产生之前，最常用的实验数据处理方法就是用误差的大小来表示[3]。误差是指测定的数值或其他近似值与真值的差，真值指一个变量本身具有的真实值，是一个理想的无法获得的值，因此，测量误差理论上也是无法确切获得的[4]。通常用约定真值来代替理论真值，约定真值是在没有系统误差的情况下，基于无限次测量获得的。由于无限次测量不可操作，且现实中无法保证重复测量条件的一致性，因此，测量误差有一定的局限性[5]。

测量值和真值之间的符合程度即为准确度，其高低通常用绝对误差来表示。“准确度”是一个定性的术语，如人们可能说，测量是“准确”的或“不准确”的[6]。精密度指在相同的测量条件下，多次重复测量结果的降服性，也有文献称之为测量结果的“一致性”。准确度高，精密度也可能比较低，反之亦然。整体不确定度小的话，则准确度和精密度都比较高。其中，系统效应产生的不确定度的品质决定了测量结果准确度的高低；随机效应引起的不确定度的品质决定了测量结果精密度的高低。它们之间的关系如图2所示。

3 评定测量不确定度的方法

3.1 测量不确定度的分类

测量不确定度分为两大类：标准不确定度和扩展不确定度[7]。测量不确定度用标准偏差表示时称为标准不确定度，常说的“合成标准不确定度”是由标准不确定度合成而求得，扩展不确定度是在合成标准不确定度的基础上乘以一个置信因子k求得。测量结果的不确定度无论用标准不确定度还是用扩展不确定度表示，都离不开将各不确定度分量合成，因此“合成”不是它们的区别，在一定程度上属于不确定度的评定手段[8]。

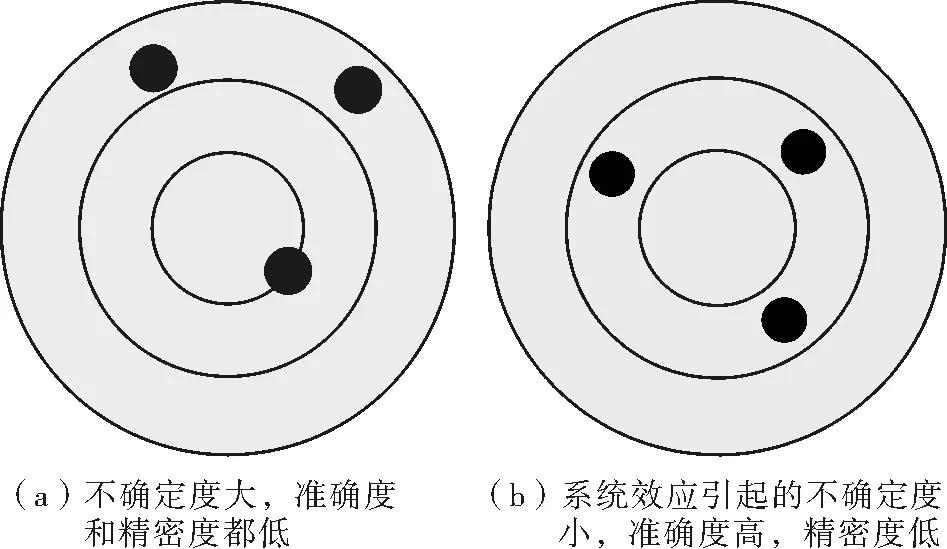
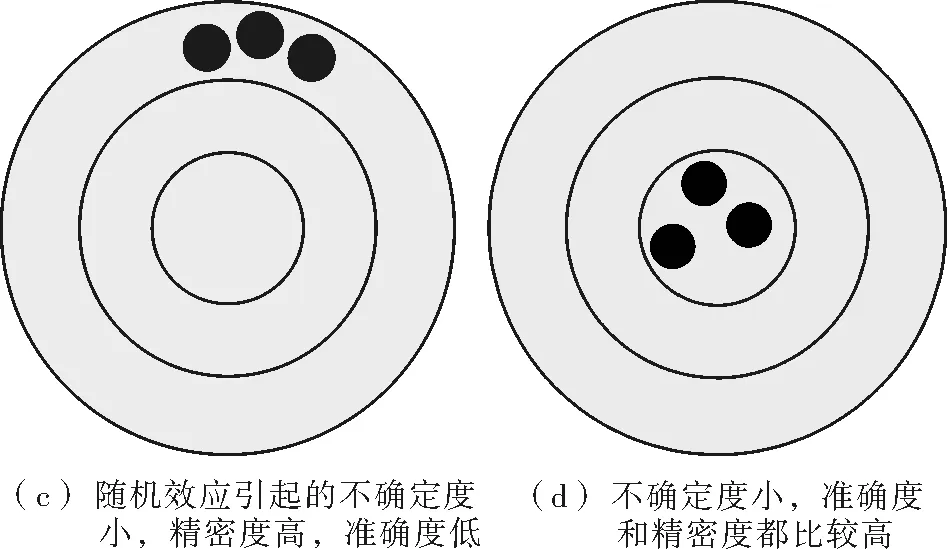
图2不确定度品质与测量结果的关系图

如果没有特殊说明，一般情况下应该给出扩展不确定度。不确定度一般不分类，如果非要分类，可以按包含因子k的大小分类，包含因子的取值主宰着扩展不确定度的置信水平：当k=1时为标准不确定度；当k≠1时为扩展不确定度。其关系如图3所示。

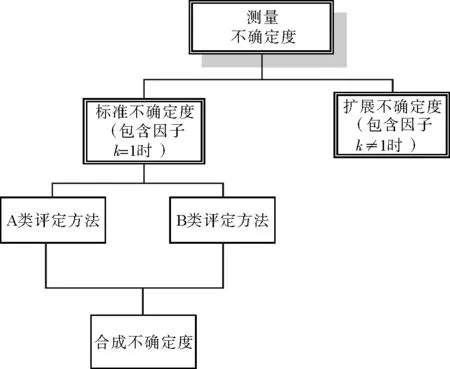
图3 测量不确定度分类关系图

不确定度评定最重要的观念之一是，要通过分析测量过程了解测量不确定度的主要来源。对不确定度来源的识别，要从仔细分析测量过程开始。这要求测量系统的设计人员和试验人员，需要采用各种方法对测量程序和测量系统做详细研究。譬如测量流程图、计算机模拟、重复测量或交替测量，与其他方法比较等。因此，测量系统的设计人员或熟练操作人员是最适合进行不确定度评定工作的。

3.2 评定测量不确定度的具体方法

由图3可知，无论是哪种测量不确定度，都是以标准不确定度为基础而进行扩展运算得到的。标准不确定度分为A类和B类评定方法：A类评定指用对观测列进行统计分析的方法，来评定标准不确定度；B类评定指用不同于对观测列进行统计分析的方法，来评定标准不确定度，通常指的是通过评估者的经验和掌握的信息分析得到的标准差。A类和B类评定方法性质并无不同，只是表明获取数据的方法不同：A类不确定度的计算有可遵循的统一方法；而B类计算方法要求具有经验和洞察力，这种技巧往往需要多次实践才能掌握[9]。A类评定方法具体步骤如表1所示。

表1 A类评定方法

B类不确定度评定是根据测量经验和有关资料及假定的概率分布估计的标准差，其原始数据并非来自观测列的数据加工，而是通过实验或其他信息来估算，有主观鉴别的因素。

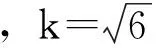
4 测量不确定度的具体评定步骤

4.1 建立数学评定模型

建立数学模型是评定不确定度的重要切入点。根据被测量的特点，用一个函数关系描述测量过程，从而确定被测量与有关量之间的函数关系，如式(1)所示。首先，要识别所有被测的输入量，通过数学函数关系用已知输入量计算最终的待测量。

Y=f(X1，X2，…，XN)

(1)

式中，Y是被测量的值；X1，X2，…，XN为影响被测量的因素[10]。

4.2 求最佳估计值

如果被测量Y的最佳估计值为y，输入量Xi的估计值为xi，则有:y=f(X1，X2，…，XN) 。通常采用式(2)来求解y。

(2)

4.3 求标准不确定度分量

分析测量不确定度的产生因素是不确定度评定的关键。确定各参数在测量过程中有哪些分量，分别属于什么性质(A类或B类)[11]；由A类方法或B类方法确定每一个不确定度分量。

4.4 标准不确定度的合成

将测量结果的所有不确定度分量进行合成即为合成不确定度。合成时需要考虑各输入量之间的相关性，通常用各分量的方差和协方差适当和的正平方根来计算。

4.5 给出扩展不确定度

4.6 测量结果最终报告

按照“JJF1059—1999”中8.3规定的不确定度报告的5个要素(包括通常输入量与输出量的函数关系及灵敏系数等)提供最终报告，通常给出合成不确定度或者扩展不确定度。若无特殊说明，通常给出扩展不确定度。推荐采用下列形式：如m=40.012 45g,Uc=0.12m，取k=2,U=2×0.12mg=0.24mg,则m=(40.012 45±0.000 24)g,k=2。

5 结束语

不确定度问题是测量工作的一项重要技术指标。通过对不确定度概念进行综述，对其评定进行分析总结，将为实验教学中不确定度的解决和应用奠定坚实的基础。

[1]管荷兰.大学物理实验中不确定度分析[J].大学物理实验，2007,20(1):75-77.

[2]张建,雷晓杰,张平萍.测量不确定度与测量误差的区别及评定方法[J].金属制品，2004,30(6)：43-45.

[3]高允峰.实验不确定度与测量误差之比较[J].长春师范学院学报,2005,24(2):144-147.

[4]毕建光，蒋桂杰，王洪平.误差、准确度、精密度和不确定度的定义以及它们之间的关系[J].建材标准化与质量管理，2004,30(1):72-75.

[5]胡林福.测量不确定度和误差的区别[J].质量技术监督研究，2009(1)：55-57.

[6]陈理渊,黄进.不确定度问题研究情况综述[J].电路与系统学报，2004,9(3):105-107.

[7]李小建.有关测量不确定度的一些基本概念[J].云南电力技术,2004,32(5):19-21.

[8]中国计量科学研究院.测量不确定度评定与表示(JJF1059—1999)[S].北京:国家质量技术监督局，1999.

[9]林奎明.B类不确定度计算方法探讨[J].计量技术,2000(3):52-55.

[10]杜怀栋.建立不确定度数学模型方法探讨[J].现代测量与实验室管理,2004(4):15-17.

[11]杨丽娟,胡在国.大学物理中不确定度表示[J].实验科学与技术,2004,2(4):8-10.

Research on Testing Uncertainty in the Experiment

LI Yanmei, FAN Yu

(School of Electronic Information and Mechanical Electrical Engineering, Zhaoqing University, Zhaoqing 526061, China)

This paper introduces the concept of measurement uncertainty to its assessment method to achieve the development of national unity.It points out the uncertainty of measurement involves the technical specifications at home and abroad, given the uncertainty, the definition of error, accuracy and precision of several concepts and analysis of their relationship.Then, two methods of evaluation of uncertainty are given, they are a kind of evaluation method and class B evaluation method, especially summarizes the concrete steps of Class A evaluation method.Finally, it summarizes the six specific evaluation steps of uncertainty: Mathematical evaluation model is set up; Strives for the best estimate; Standard uncertainty components; Synthetic standard uncertainty.Finally, the expanded uncertainty put forward the report of uncertainty.

measurement uncertainty; evaluation; method; experiment

2014-06-23；修改日期:2014-07-21

李艳梅(1981-)，女，硕士，工程师，主要从事微电子、实验室管理方面的研究。

Adoi:10.3969/j.issn.1672-4550.2015.06.010