基于物像位置关系研究凸面镜成像规律
2015-02-27刘春晓訾振发
刘春晓,訾振发
(1.南京邮电大学 光电工程学院,江苏 南京 210023; 2. 合肥师范学院 电子信息工程学院,安徽 合肥 230601)
基于物像位置关系研究凸面镜成像规律
刘春晓1,訾振发2
(1.南京邮电大学 光电工程学院,江苏 南京 210023; 2. 合肥师范学院 电子信息工程学院,安徽 合肥 230601)
[摘要]凸面镜在生活生产和科学研究中发挥着越来越重要的作用。传统的作图法定性地描述了凸面镜的成像规律,已经不能满足人们对凸面镜成像精确度的需求。本文利用物像位置关系公式,推导了凸面镜的垂轴放大率,得出了凸面镜成像规律的数学描述,实现了对凸面镜成像规律的定量研究。
[关键词]凸面镜;成像规律;物像位置关系;垂直放大率
利用球面的外表面作为反射面的球面镜叫做凸面镜。凸面镜也称为反光镜、广角镜和转弯镜。它是仅次于平面镜的简单光学元件,在日常生活和工业生产中都有着广泛的应用。凸面镜经常被用作汽车后视镜,扩大驾驶者的视野范围。在“L”或“T”形交通路口通常也树立一面凸面镜,以瞭望对面的行人和车辆运行情况,减少交通事故的发生[1]。大型商场和超市常常采用凸面镜监视死角,防止商品被偷盗。另外,凸面镜也是大多数现代光学系统的基本组成单元,受到了科技工作者的广泛青睐。凸面镜是成像光谱仪中Schwarzschild结构的重要构成部分,为成像光谱仪的连续多光谱成像和精细的光谱区分提供了支持[2-4]。光学谐振腔是激光器的三个主要组成部分之一。凸面镜可以构成双凸腔、平凸腔和凹凸腔等光学谐振腔,为得到稳定持续、有一定功率、高质量的激光输出奠定了基础[5-7]。啁啾脉冲放大技术已经成为超短超强激光脉冲产生的重要途径。凸面镜是飞秒激光啁啾脉冲放大系统中的折叠反射式望远镜系统的基本组成部分,对脉冲波前和光束质量都产生了重要的影响[8]。凸面镜之所以能够有这么多重要的应用,是因为它通常成缩小、正立的虚像并且有很大的成像范围。常见的文献资料或教科书一般都是定性或者通过作图的方式给出凸面镜的成像规律[1, 9-11]。作图法虽然可以使人一目了然地看清事物的变化趋势,但是处理数据的精度较低而且不能反映引起现象变化的内在原因。因此,作图法在某些需要较高精密度的现代光学研究领域(例如上面提到的成像光谱仪,激光器和啁啾脉冲放大系统等研究领域)就受到了一定的限制。然而,随着凸面镜在高新技术中应用的不断加强,对凸面镜成像的精确计算的需求变得越来越紧迫。物像位置公式是工程光学或应用光学中最基本的公式之一,在近轴光线的光路计算中占据着重要的位置[1, 9-11]。物像位置公式描述了光学系统的物象关系,是研究光学系统成像特性的重要解析方法,表明了物、像之间位置的精确关系。换句话说,如果已知了物体的位置,即可通过物像位置公式准确地求出其共轭像的位置。本文将通过物像位置公式定量地推导出凸面镜的成像规律,得出的凸面镜垂直放大率可以精确地计算凸面镜成像的大小,并且有助于初学者理解凸面镜成像规律的物理本质。
1凸面镜成像规律
作图法可以直观、清晰和形象地了解光学系统成像的正倒、虚实、放大与缩小等情况。下面我们首先按照一般的文献资料或教科书的思路,利用作图法得出凸面镜的成像规律[1, 9-11]。作图时,通常选择以下几条特殊光线[9]。第一,平行于光轴入射的光线,它经过光学系统后过像方焦点。具体应用到本文所研究的凸面镜中,相应的反射光线的延长线通过凸面镜的焦点。第二,通过焦点的光线或入射光的延长线通过焦点的光线,它经过光学系统后平行于光轴。第三,通过曲率中心的光线,它经过光学系统后和入射光线在同一直线上。图1就是利用这些特殊光线给出了物体AB经过凸面镜后所成的像A′B′。图中,O为凸面镜的顶点,F′为像方焦点,C为球心。由图可见,凸面镜成正立、缩小的虚像(光线反向延长线的交点)。
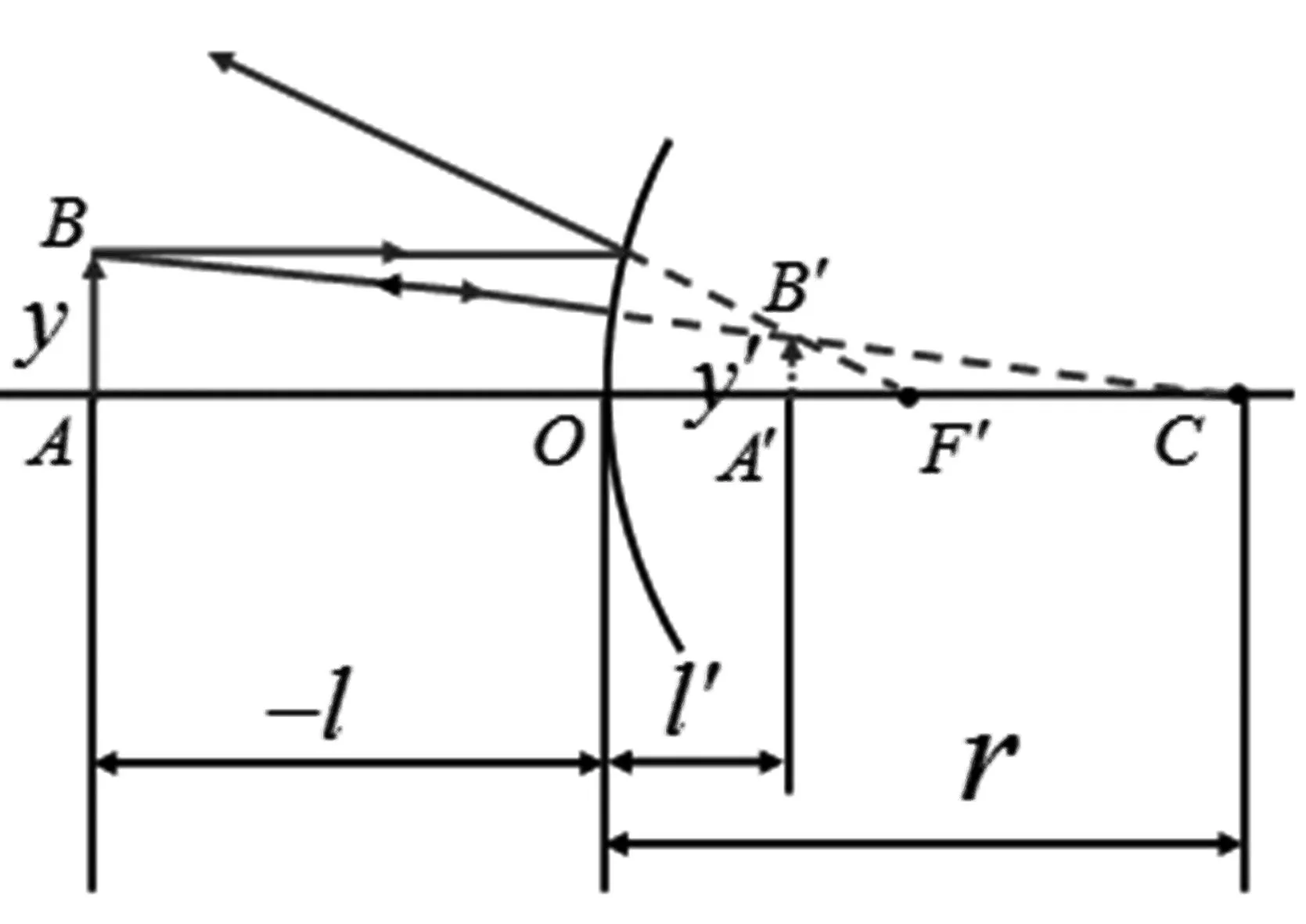
图1 凸面镜成像示意图
2凸面镜物像位置公式
为了利用物像位置公式描述光学系统物像的相对位置和大小等物理量,需要引入符号规则以确定各量的正负号。本文选用的是郁道银和谭恒英主编的《工程光学》中提到的符号规则[1]。这个符号规则的第一条表述为:“沿轴线段:规定光线的传播方向自左至右为正方向,以折射面顶点O为原点,由顶点到光线与光轴交点(A, A′)或球心(C)的方向和光线传播方向相同时取正,相反时取负”。因此,图1中的物方截距记作-l,像方截距表示为l′,球面曲率半径记为r。根据该符号规则的第二条:“垂轴线段:以光轴为基准,在光轴以上为正,在光轴以下为负。”,则图1中物AB的大小记作y,像A′B′的大小表示为y′。值得注意的是,图1所示的凸面镜成像示意图中各量都是几何量,都用绝对值表示。也就是说,凡是负值的量,图中相应量的符号前面都要加上负号。
单个折射球面的物象位置关系为[1]:
(1)
式中,n和n′分别表示物方和像方的折射率。反射定律可以看做是折射定律的特殊情况,凡是基于折射定律推导得到的光线经过界面折射有关的公式,只要令n′=-n便可以得到光线经过界面反射时的有关公式[11]。因此,将式(1)中的n′替换为-n便可以得出凸面镜的物像位置公式。即:
(2)
3物像位置关系推导凸面镜成像规律
上面对凸面镜成像规律和物像位置公式分别作了简要的介绍,接下来就利用得出的凸面镜物像位置公式(即式(2))从理论上给出凸面镜成像规律的推导过程。垂直放大率(也称为横向放大率)是探明光学系统成像规律的重要参量,用来描述物体成像前后高度之间的关系。因此,我们就从垂直放大率入手研究凸面镜的成像规律。
垂直放大率定义为像的大小与物的大小之比,一般用表示β。在图1所示的凸面镜成像中,β即为y′和y的比值,如下式所示。
(3)
根据式(3),可以确定光学系统的成像特性,即像的正倒、虚实、放大与缩小。
对于凸面镜,在图1中ΔA′B′C和ΔABC相似。所以,
(4)
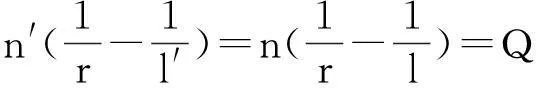
(5)
式中,Q为阿贝不变量[1]。

(6)
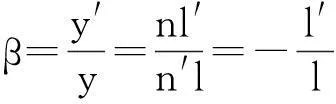
(7)
上式再次利用了“反射是折射在n′=-n时的特例”的原理[1]。由式(2)可得,
(8)
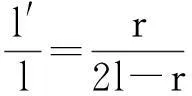
(9)
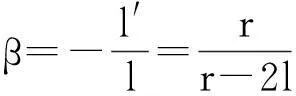
(10)
式(10)就是通过物像位置关系公式得出的凸面镜垂直放大率。由符号规则可知:l<0且r>0,故0<β<1。β>0,即y′和y符号相同,表示成正立的像;同时,β<1,表示成缩小的像。另外,l′和l符号相反,物像虚实相反,即凸面镜成虚像。所以,凸面镜成正立、缩小的虚像。至此,我们通过物像位置公式等解析方法推导了凸面镜成像的放大率并且从数学的角度分析得出了凸面镜成正立、缩小的虚像的成像规律。
4结论
凸面镜是构成光学系统的基本单元,物像位置公式是研究光学系统成像的基本理论。

[参考文献]
[1]郁道银,谈恒英.工程光学[M]. 北京:机械工业出版社,2012:10-13.
[2]刘建芳. 改进型高分辨率宽波段Schwarzschild成像光谱仪研究[J]. 光谱学与光谱分析,2013, 33(8) 2286-2289.
[3]张晶,薛庆生,曹佃生. 基于双Schwarzschild结构的平面光栅光谱仪[J].光学精密工程,2014, 22(9) 2321-2328.
[4]胡大伟,李艳秋,刘晓林. 超高数值孔径Schwarzschild投影光刻物镜的光学设计[J]. 光学学报,2013, 33(1) 0122004.
[5]马惠军,孟俊清,李小莉,朱小磊,陆雨田. 高功率高重复频率全固态激光器热透镜效应补偿与分析[J]. 强激光与粒子束,2005, 17(4) 175-179.
[6]陆宇灵,孔小健,曹华梁. CO2激光器虚共焦腔凸面镜失调的实验研究海[J]. 海军工程大学学报,2007,19(6) 50-52.
[7]杜少军,陆启生,舒柏宏,王默戈. 激光辐照下非稳腔镜变形对激光模式的影响[J]. 强激光与粒子束,2007,19(1) 53-57.
[8]韩英魁,王清月,张志刚,张伟力,柴路,袁晓东,黄小军. 飞秒啁啾脉冲放大系统中折叠反射式望远镜对脉冲波前的影响[J]. 物理学报,2005,54(4) 1613-1617.
[9]程守洙,江之永.普通物理学(下册)[M]. 北京:高等教育出版社,2006:112-118.
[10]张以谟.应用光学[M]. 北京:电子工业出版社,2008:18-24.
[11]石顺祥,王学恩,刘劲松. 物理光学与应用光学[M]. 西安:西安电子科技大学出版社,2008:327-337.
An Investigation on Imaging Laws of Convex Mirrors by Location Relationship between Objects and Images
LIU Chunxiao1, ZI Zhenfa2
(1.SchoolofOptoelectronicEngineering,NanjingUniversityofPosts&Telecommunications,
Nanjing210023,China;
2.SchoolofElectronicandInformationEngineering,HefeiNormalUniversity,Hefei230601,China)
Abstract:Convex mirrors play an important role in the industry and scientific research. Investigations on imaging laws of convex mirrors by the traditional graphing method cannot meet the demand for accuracy. The location relationship between objects and images is utilized to obtain the lateral (or transverse) magnification of convex mirrors in the present work. The mathematical expression of the imaging law of convex mirrors is derived from the analysis of the lateral (or transverse) magnification.
Key words:convex mirror; imaging law; location relationship between objects and images; lateral (or transverse) magnification
[中图分类号]G61
[文献标识码]A
[文章编号]1674-2273(2015)06-0036-02
作者简介][第一 刘春晓(1982-),男,安徽六安人,博士,南京邮电大学光电工程学院副教授。主要从事光波导、光隔离器和光纤激光器等方面的研究工作。
[基金项目]南京邮电大学引进人才科研启动基金(NY214159),大学物理及实验教学团队(2013jxtd02),普通物理学教改示范项目(2011jgsf02)
[收稿日期]2015-06-05
