空间桁架热致振动效应仿真研究

苏新明王晶，2张军徽向志海

（1北京卫星环境工程研究所，北京 100094）

（2北京卫星环境工程研究所可靠性与环境工程技术重点实验室，北京 100094）

（3清华大学航天航空学院，北京 100084）

空间桁架热致振动效应仿真研究

苏新明1王晶1，2张军徽3向志海3

（1北京卫星环境工程研究所，北京 100094）

（2北京卫星环境工程研究所可靠性与环境工程技术重点实验室，北京 100094）

（3清华大学航天航空学院，北京 100084）

基于傅里叶（Fourier）温度单元及Boley理论，分析了不同条件下某大型柔性空间结构（LFSS）的热致振动情况，发现改变悬吊杆长度、配重总质量以及背景温度均会影响结构振动幅值和准静态变形之比，但背景热流的影响更大，且其对降低结构的热特征时间有明显作用。入射热流的改变对结构热致振动无明显作用，仅能够改变结构的振动幅值和准静态变形。以上研究结果可有助于改进航天器LFSS结构设计，避免出现在轨热致振动现象。

大型柔性空间结构；热特征时间；热致振动

1 引言

航天器大型柔性空间结构（Large Flexible Space Structures，LFSS）因其尺寸大、质量轻、刚度低和热容较小等特点，在轨受到极端热载荷的影响造成温度在结构上分布不均，从而在结构内部产生不均匀的热应变，进而引发LFSS的热致振动问题。自20世纪60年代以来因热诱发振动引起众多航天器失效事件［1］，其中最为著名的是1990年哈勃太空望远镜（HST）太阳翼在昼夜交替时发生持续扭转振动，造成望远镜成像模糊畸变事故［2］。

1956年，Boley［3］首次提出了热诱发振动的概念，并在理论上进行了解释。其将瞬态热弯矩引入热致结构响应分析中，并给出了判断结构是否会发生热诱发振动的参数即Boley参数［4］（B＝tT/tω）。当结构的热特征时间tT与结构的最大振动周期tω之比不大于1时，则结构将会发生热诱发振动。随后一批学者以简单的梁模型研究梁的热诱发振动问题，如Thornton［2］等人利用梁模型分析了哈勃太空望远镜太阳翼弯曲振动变形引起吸收热流的变化，进而造成结构动力学响应与瞬态温度场耦合，并给出了弯曲振动稳定性的判据。1968年，Mason［5］首次将有限元方法引入热诱发振动分析，并与理论解做了对比，验证了计算方法的可靠性。1993年，Rand和Givoli［6-7］发展了一种新的温度单元，他们将薄壁管截面内的温度场表述为平均温度和摄动温度的叠加，将二维温度场问题转化为一维温度场问题进行温度场的有限元分析。此方法能使用同一套网格对结构的温度场和变形场进行求解，大大地减小了计算量。然而，这种单元的平均温度和摄动温度耦合在一起，若用于热诱发振动分析，计算效率很低。2002年以来，薛明德等人［8-10］在Rand等人工作的基础上提出了傅里叶（Fourier）温度单元，通过选取合适的形函数获得了解耦的平均温度有限元方程和摄动温度有限元方程，将非线性分析局限在平均温度场的求解中，可高效地用于瞬态热-结构动力学的计算。随后，采用Fourier温度管单元将Boley理论扩展至复杂结构［11-12］，采用热模态分析的方法求解LFSS的热特征时间tT，并提出了大型结构热诱发振动的稳定性分析方法。薛明德等人的工作促进了热致响应分析的工程化，为分析LFSS的热致响应提供了有力的工具。

以上学者的研究多集中在仿真分析的理论及方法上面，对于复杂结构产生热致振动的众多影响因素分析较少。本文即在薛明德等人的研究基础上，对某待测试空间桁架试验件开展热致振动仿真计算，分析了不同参数条件下该桁架的热致振动效果，基于结果提出了可以抑制LFSS的在轨热致振动的方法。

2 物理模型

某空间桁架外观如图1所示［13］，桁架长2.8 m，截面尺寸0.8 m×0.8 m，由4个相同的构架单元组成。构架单元由纵梁组件、球铰接头、斜拉索组件及横向框架等组成，其材料及几何特性如表1所示。

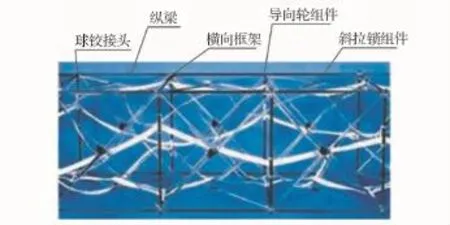
图1 某空间桁架外观Fig.1 View of a space truss

表1 空间桁架材料及几何特性Table 1 Material and geometry characteristics of the space truss

经分析，仅有4个构架单元的桁架其刚度较高，很难在试验条件下发生热致振动现象。为此对桁架进行了改造，通过延长桁架长度以及增加配重的方式增加其柔性以及降低结构的基频，使热致振动现象更易发生。在桁架―x侧顶端4个角点处安装一直径为30 mm的铝合金十字连接杆，并在其中心焊接一根起延长作用并可用于悬挂的铝合金管。该铝管外径5 mm，壁厚1 mm，它的另一端设置了机械接口可以用于将桁架悬挂固定。此外，在桁架＋x侧底端的4个角点上分别设置相同的集中质量。改造后的桁架物理模型如图2所示。本文讨论不同悬吊杆长度、配重总质量、不同入射热流强度以及不同背景温度作用下，该桁架的热致振动情况。图2中，A、B两点用于分析结构的动态响应以及端部稳定后温差，其中入射热流垂直照射A点所在一侧的桁架，悬吊杆以及配重不受照，后文分析中均将按此设置。

图2 改造后的空间桁架物理模型Fig.2 Physical model of changed space truss

3 基本方程

本文采用段进、程乐锦、薛明德等人提出的关于空间桁架结构热致振动问题的有限元求解方法，对桁架的热致振动问题进行仿真计算。

根据桁架结构的特点，分析其温度场和热致响应的特点，引入基本假设［14］：

（1）薄壁杆的壁厚很小，所以忽略沿壁厚方向的温差，假定温度沿壁厚方向均匀分布；

（2）假定杆截面的摄动温度远小于平均温度，即认为杆截面内的温差相对其平均绝对温度而言是小量；

（3）考虑薄壁杆外表面的辐射换热，但忽略其内表面相互之间的辐射换热；

（4）开口薄壁杆剖面处为绝热边界，忽略开口剖面处的热交换；

（5）假定材料性质不随温度变化。

根据上述假设，采用傅里叶温度单元进行薄壁杆结构的瞬态温度场计算。该单元同样将管截面的温度场表示为平均温度和摄动温度的叠加，并将平均温度和摄动温度沿轴向进行线性插值，通过选取合适的形函数获得了解耦的平均温度有限元方程和摄动温度有限元方程［14］，将非线性分析局限在平均温度场的求解中，大大减小了计算量，可高效地用于瞬态热-结构动力学的计算。

对于图2所示的桁架，其由薄壁管组成，因为管的长度比截面尺寸大的多，所以结构模型选用梁模型。在热-结构耦合分析阶段，假设梁的变形满足以下假设［15］：

（1）变形前垂直于梁的中心线的截面变形后仍然垂直于中心线（Kirchhoff假设）；

（2）梁的纵向纤维互不挤压，即略去梁横截面内的正应力；

（3）变形前垂直于中面的截面扭转变形后仍然保持平面（不考虑扭转引起的翘曲）。

根据梁单元的热弹性本构关系，将瞬态温度场分析所得的结构温度场转化为作用在结构上的等效温度载荷，建立热-结构耦合动力学方程。由于耦合项的存在，热-结构耦合动力学方程需要迭代求解。采用Newmark方法和Newton-Raphson方法联合迭代求解的方法求解热-结构耦合动力学方程［14］。

将桁架结构的节点温度T分解为沿结构周向的平均温度T（0）（t）和摄动温度T（1）（t）［14，16］，其中t为时间，两者满足：

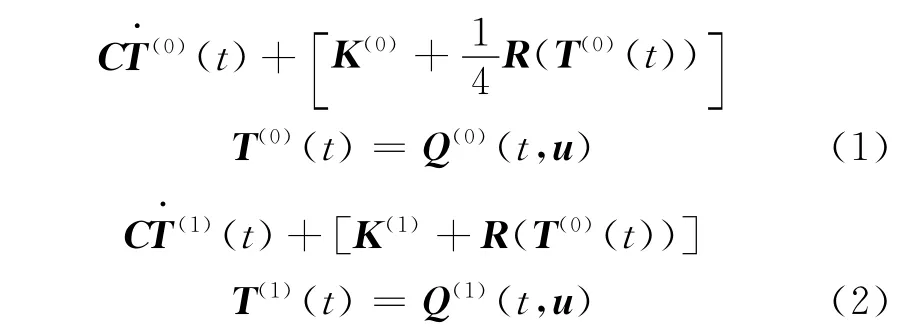
式中：C为热容矩阵，K（0）、K（1）为热传导矩阵，R（T0（t））为热辐射系数矩阵；Q（0）（t，u）、Q（1）（t，u）为热流载荷项；u为t时刻的广义位移矢量。

将温度载荷引入结构动力学方程［14-15］，得到

式中：M、D和K分别为质量、阻尼与刚度矩阵；P是载荷项，此时主要考虑由温度引起的载荷。

对于空间桁架，在整个时间域内有［11］

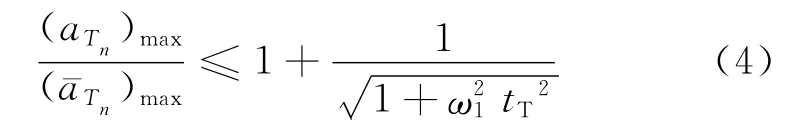
式中：（aTn）max为结构的最大动态响应；（Tn）max为结构的最大准静态响应；ω1为结构振动1阶固有圆频率；tT为结构的热特征时间，本研究中，tT用A、B两点温差达到稳定所需的最短时间表征。ω1、tT均为结构的固有特性。

可见，当ωtT很小时，结构发生热致振动的可能性就越大，反之，结构响应中准静态成分就越多，从而不会发生热致振动。

4 计算条件及简化

计算条件设置见表2。

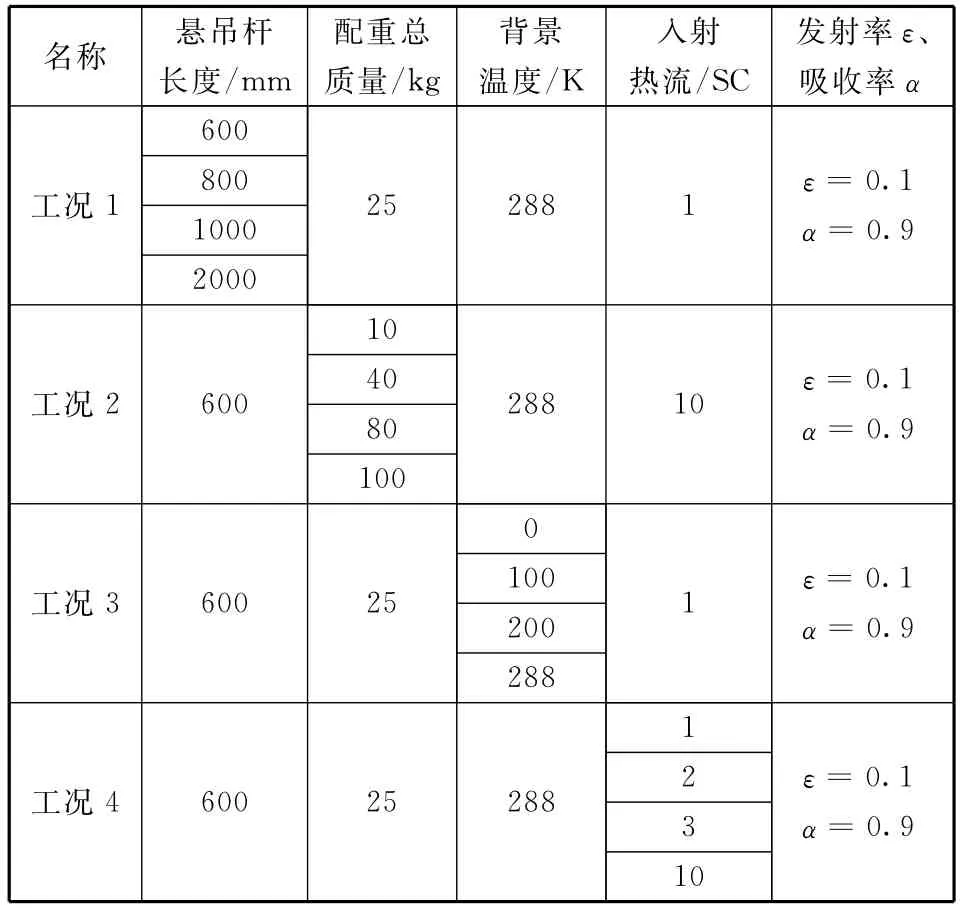
表2 计算条件Table 2 Computation conditions

在建立的桁架有限元模型中，进行了如下简化：

（1）紧固件作为相应杆件的一部分，而不单独建模；

（2）在每个斜拉索的交点处划分很短的十字交叉的梁单元，通过设定这些梁单元的密度，以模拟斜拉索锁体对结构的影响；

（3）斜拉索的预应力通过设定拉索材料的参考温度获得。

5 仿真结果及分析

图3～图10分别给出了各工况下，桁架上A点的Y向位移以及A、B两点的温度差随时间的变化情况。图3、图4显示，随着悬吊杆长度增加，结构刚度降低，所以准静态变形逐渐增大，振动幅值和准静态变形之比也逐渐增大。但悬吊杆长度的改变并不影响A、B两点温差。图5、图6显示，随着配重总质量的增加，准静态位移逐渐增大，振动幅值和准静态变形之比逐渐增大。此时配重总质量的改变仍不会改变A、B两点之间的温差。所以，不论是增加悬吊杆长度还是改变配重质量，在图4、图6中A、B两点间的温差曲线均是重合的。

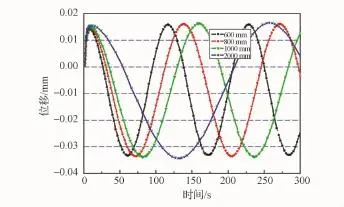
图3 工况1时A点的Y向位移Fig.3 Case 1，displacement of point A in Y direction

图4 工况1时A、B点之间的温差Fig.4 Case 1，temperature difference between point A and point B

图5 工况2时A点的Y向位移Fig.5 Case 2，displacement of point A in Y direction

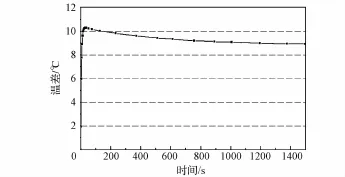
图6 工况2时A、B点之间的温差Fig.6 Case 2，temperature difference between point A and point B

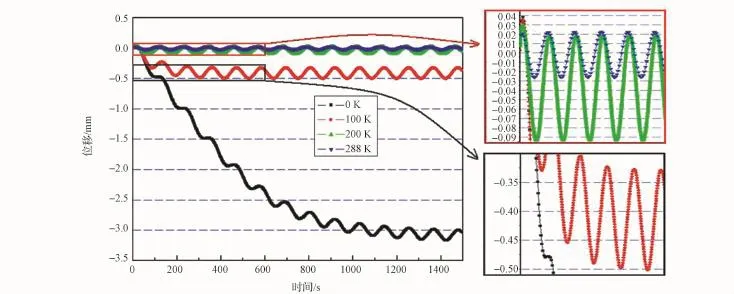
图7 工况3时A点的Y向位移Fig.7 Case 3，displacement of point A in Y direction

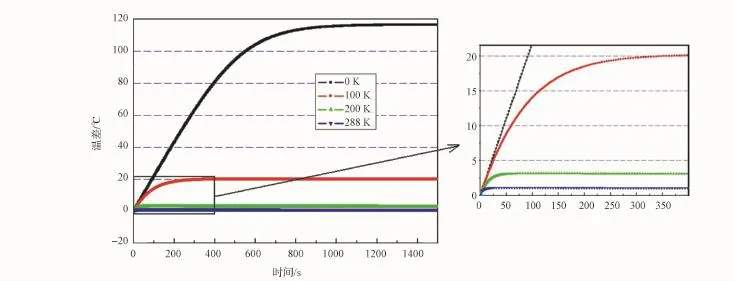
图8 工况3时A、B点之间的温差Fig.8 Case 3，temperature difference between point A and point B

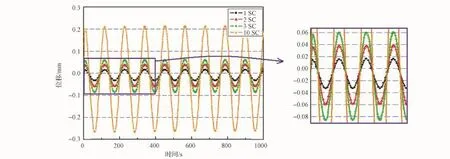
图9 工况4时A点的Y向位移Fig.9 Case 4，displacement of point A in Y direction

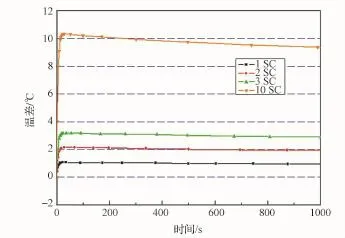
图10 工况4时A、B点之间的温差Fig.10 Case 4，temperature difference between point A and point B

图7、图8显示，由于背景温度不同，造成了不同条件下A、B两点之间的温差出现差异，结合式（2）可知：随着背景温度的提高，等效导热系数 ［K（1）＋R（T（0）（t））］变大，导致上下表面温差逐渐减小，结构的热特征时间减小，结构准静态热变形和热诱发振动的幅值都逐渐减小，但振动幅值和准静态变形之比逐渐增大。

图9、图10显示，尽管温差有差异，但增加热流并不改变结构的热特征时间，所以振动幅值和准静态变形之比几乎不变。但由于结构上下表面温差会增大，振动幅值和准静态变形都同时变大。而且振动幅值与热流值近似正比关系。

以上结果表明：各条件下，桁架均发生了热致振动；相较于增加悬吊杆长度、配重总质量，背景温度大小对于改变桁架的振动幅值和准静态变形之比的作用更明显；提高背景温度，对于降低试验件的热特征时间有明显作用，更利于结构发生热致振动；入射热流的改变并不影响结构的热特征时间，且振动幅值和准静态变形之比几乎不变，但能够增大结构的振动幅值和准静态变形。

6 结论

本文介绍了某空间桁架的组成，并对不同参数条件下的该桁架的热致振动情况进行了仿真计算，通过比较、分析桁架上选定位置的温差及位移随时间的变化情况，可以得出以下结论：

（1）对于航天器LFSS设计应充分考虑结构长度、端部质量所带来的影响，为防止结构发生热致振动现象，在满足长度要求的同时，桁架结构应开展轻量化刚性设计，端部载荷应采取减重设计。

（2）在轨为4 K的冷黑背景，其温度相对稳定，对LFSS热致振动作用不明显。但在地面试验条件下，可充分利用背景温度进行相关的试验验证，如调节背景温度升高，可使结构更加容易出现热致振动。

（3）可改变结构表面的吸收率和发射率，进而降低入射热流的影响，从而抑制结构的准静态变形。

本文的结论是基于仿真结果得出，其正确性已经得到验证，具体可参考文献［17］。但是该分析手段目前还未应用于航天器，因此还无法与航天器试验数据进行对比，后续需要在此方面重点开展工作。

（References）

［1］Thornton E A.Thermalstructures for aerospace applications［C］.AIAA Education Series.Washington D.C.：AIAA，1996

［2］Thornton E A，Kim Y A.Thermalinduced bending vibrations of a flexible rolled-up solar array［J］.Journal of Spacecraft and Rockets，1993，30（4）：438-448

［3］Boley B A.Thermallyinduced vibrations of beams［J］. Journal of Aeronautical Sciences，1956，23（2）：179-181

［4］Boley B A.Approximateanalyses of thermally induced vibrations of beams and plates［J］.Journal of Applied Mechanics，Transactions of the ASME，Series E，1972，39（1）：212-216

［5］Mason J B.Analysis of thermally induced structural vibrations by finite element techniques，NASA TM X-63488［R］.Washington D.C.：NASA，1968

［6］Rand O，Givoli D.A finite-element spectral method with application to the thermoelastic analysis of space structures［J］.International Journal for Numerical Methods in Engineering，1990，30（2）：291-306

［7］Givoli D，Rand O.Harmonic finite-element thermoelastic analysis of space frames and trusses［J］.Journal of Thermal Stresses，1993，16（3）：233-248

［8］Xue M D，Ding Y.Twokinds of tube elements for transient thermal-structural analysis of large space structures［J］.International Journal for Numerical Methods in Engineering，2004，59（10）：1335-1353

［9］丁勇，薛明德.辐射换热条件下空间薄壁圆管结构瞬态温度场、热变形有限元分析［J］.宇航学报，2002，23（5）：49-56 Ding Yong，Xue Mingde.Thermal-structural finite element analysis of space structures consisting of thin walled beams［J］.Journal of Astronautics，2002，23（5）：49-56（in Chinese）

［10］丁勇.大型空间结构的热―结构有限元分析［D］.北京：清华大学工程力学系，2002 Ding Yong.Thermal-dynamic analysis of large-scale space structures by FEM［D］.Beijing：Tsinghua University，2002（in Chinese）

［11］程乐锦，薛明德，唐羽烨，等.大型空间结构的热-动力学分析［J］.应用力学学报，2004，21（2）：1-9 Cheng Lejin，Xue Mingde，Tang Yuye，etc.Thermaldynamic analysis of large scale space structures by FEM［J］.Chinese Journal of Applied Mechanics，2004，21（2）：1-9（in Chinese）

［12］程乐锦.大型空间结构的热诱发振动有限元分析［D］.北京：清华大学工程力学系，2003 Cheng Lejin.Thermally induced vibration analysis of large space structures using the finite element method［D］.Beijing：Tsinghua University，2003（in Chinese）

［13］檀傈锰，白化同，程刚，等.大型可展收支撑臂模态试验研究［J］.航天器工程，2012，21（6）：125-130 Tan Limeng，Bai Huatong，Cheng Gang，et al.Study on modal test of large deployable support beam［J］. Spacecraft Engineering，2012，21（6）：125-130（in Chinese）

［14］薛明德，向志海.大型空间结构的热-动力学耦合问题及其有限元分析［J］.固体力学学报，2011，32：318-328 Xue Mingde，Xiang Zhiha.Thermal-dynamic coupling problem of large space structures and its FEM analysis［J］.Chinese Journal of Solid Mechanics.2011，32：318-328（in Chinese）

［15］段进.大型柔性空间结构的热-动力学耦合有限元分析［D］.北京：清华大学工程力学系，2007 Duan Jin.The thermal-dynamic coupling analysis of large flexible space structures by finite element method［D］.Beijing：Tsinghua University，2007（in Chinese）

［16］段进，薛明德，向志海，等.辐射换热下瞬态热-结构分析的一种空间薄壁杆单元［J］.计算力学学报，2007，24（6）：345-351 Duan Jin，Xue Mingde，Xiang Zhihai，etc.A kind of thin-walled beam element for transient thermal-structural analysis considering radiation heat transfer［J］. Chinese Journal of Computational Mechanics，2007，24（6）：345-351（in Chinese）

［17］Su X M，Zhang J H，Wang J，et al.Experimental investigation of the thermally induced vibration of a space boom section［J］.Science China Physics，Mechanics&Astronomy，2015，58（4）：1-9

（编辑：李多）

Numerical Simulating Investigation of Thermally-induced Vibration of Space Truss

SU Xinming1WANG Jing1，2ZHANG Junhui3XIANG Zhihai3
（1 Beijing Institute of Spacecraft Environment Engineering，Beijing 100094，China）
（2 Science and Technology on Reliability and Environmental Engineering Laboratory，Beijing Institute of Spacecraft Environment Engineering，Beijing 100094，China）
（3 School of Aerospace Engineering，Tsinghua University，Beijing 100084，China）

Based on the Fourier temperature cell and the Boley theory，thermally-induced vibration of a large flexible space truss（LFSS）is analysed，and it is found that the ratio of the structure vibration magnitude to the quasi-static deformation could be affected by the change of the length of the suspending tube，appending mass and ambient temperature.Among these，the effect of the ambient temperature would be the most marked，and the thermal characteristic time is reduced obviously.Otherwise，the change of the incidence heat flux can affect the structure vibration magnitude and the quasi-static deformation，but has less influence on the thermally-induced vibration.The above results can help improve the LFSS design，and avoid the thermally-induced vibration.

LFSS；thermal characteristic time；thermally-induced vibration

V414.1

：ADOI：10.3969/j.issn.1673-8748.2015.05.010

2015-08-24；

：2015-09-07

苏新明，男，工程师，从事航天器热试验技术研究工作。Email：xmsu85@163.com。