基于ASIFT道路交通标志的定位与识别方法*
2015-02-26焦再强吕玉祥马维青赵晓龙李孟春
焦再强,吕玉祥,马维青,赵晓龙,李孟春*
(1.太原理工大学物理与光电工程学院,太原030024; 2.阳泉供电分公司,山西阳泉045000)
基于ASIFT道路交通标志的定位与识别方法*
焦再强1,吕玉祥1,马维青2,赵晓龙2,李孟春1*
(1.太原理工大学物理与光电工程学院,太原030024; 2.阳泉供电分公司,山西阳泉045000)
摘要:针对智能交通系统中的交通标志识别,提出了一种基于ASIFT(仿射尺度不变特征变换)算法的定位与识别方法。首先,分类道路交通标志并提取模板;然后,采用ASIFT算法选择目标图像对应的模板和交通标志集合;其次,根据匹配模板ASIFT特征点的几何分布,定位交通标志的目标区域;最后,计算目标区域和交通标志集合的特征向量欧氏距离。基于ASIFT算法,达到了准确的定位与识别效果。通过实验,验证了该方法的可行性。
关键词:仿射尺度不变特征变换;交通标志;定位;识别
项目来源:国家自然科学基金项目(61274089)
随着城市化进程的推进,道路交通安全和运输效率问题日益突出。作为解决道路交通问题的重要方案,智能交通系统ITS(Intelligent Transport System)应运而生。在ITS中,交通标志识别是一个重要的技术环节,由于应用环境复杂,目前尚不成熟[1]。而交通标志传递的丰富信息对于规范交通运行,确保道路安全以及提高运输效率有着重要作用。因此,交通标志识别成为了当前的研究热点。交通标志识别分为定位与识别两个部分,而定位与识别又相辅相成。鉴于此,本文提出了一种基于ASIFT算法[2]的定位与识别方法。借助ASIFT算法良好的仿射不变性,该方法在一定程度上克服了光照,噪声以及视觉条件的影响,达到了较好的定位与识别效果。
1 ASIFT仿射不变性
David Lowe于1999年提出了SIFT(尺度不变特征变换)算法,并于2004年作了进一步的完善总结[3]。SIFT算法对图像间的平移、旋转和尺度缩放[4]保持了良好的匹配能力。Yu和Morel在SIFT算法的基础上,于2009年提出了ASIFT(仿射尺度不变特征变换)算法。ASIFT算法保留了SIFT对平移、旋转和尺度缩放的特征提取方法,增加了空间描述参量经度角和纬度角的特征提取[2]。因此,在继承SIFT算法优点的同时,ASIFT算法对视角角度也具有完全不变性[2]。
2 交通标志的定位
基于ASIFT算法的交通标志定位过程可以描述如下: (1)模板与目标ASIFT特征匹配; (2)交通标志几何定位; (3)交通标志ROI提取。
2.1模板与目标ASIFT特征匹配
为了减少ASIFT特征匹配过程中的计算量,首先对GB 5768.2—2009文件公布的道路交通标志进行分类并提取模板。以禁令标志为例,可以得到如图1(a)所示的10个模板。对应每个模板,均有一个交通标志集合与之对应,图1(b)中显示了bm1模板及其对应集合中的部分交通标志图像。
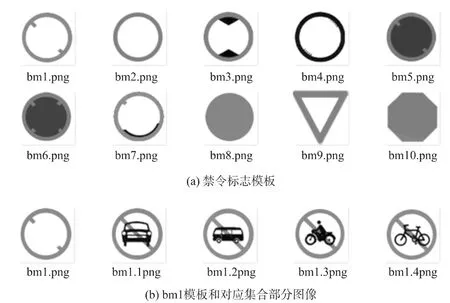
图1
采用ASIFT算法对模板和目标图像进行特征点匹配[5],并从匹配结果中选择匹配程度最优的一个模板。根据该模板的信息,确定目标图像所含交通标志对应的集合;同时,记录特征点在该模板和目标图像中的像素坐标分布[5]。
2.2交通标志几何定位
根据特征点的像素坐标分布和模板及目标图像的特征点仿射关系,理论上能够计算出交通标志的外轮廓。但是,受ASIFT算法对特征点识别率的影响,特征点的仿射关系会发生小概率错误。错误的仿射关系给最终的计算结果造成了较大的误差,使计算趋于发散。
针对上述情况,本文提出了一种新的定位方法来解决上述问题。该方法首先统计并提取特征点较为密集的区域,然后计算各个区域的重心坐标。假设密集区域A包含N个特征点,第i(0<i<N+1)个特征点的像素坐标为(xi,yi),区域A重心坐标G(x,y)的计算方式如下:

通过上述方法,在模板中,计算得到特征点密集区域的重心坐标序列。同理,从目标图像对应的特征点密集区域中,计算得到对应的重心坐标序列。在模板的重心坐标序列中,根据如下两个条件选取3个重心点:⑪三个重心点非共线;㉒任意两个重心点的连线与模板边界相交。

图2 模板几何图
如图2所示,设选取的非共线重心点及坐标分别为A(xA,yA),B(xB,yB),C(xC,yC),模板图像的4个顶点及坐标分别为O1(XL,YU)、O2(XR,YU)、O3(XL,YD)、O4(XR,YD),通过模板4个边的直线分别记作a,b,c,d。根据A、B、C 3个点的选取条件,直线AB与直线a,直线b,直线c,直线d分别相交于点U1、点L1、点D1、点R1;直线AC分别与直线a、直线b、直线c、直线d相交于点U2、点L2、点D2、点R2。8个向量分别满足下列公式:
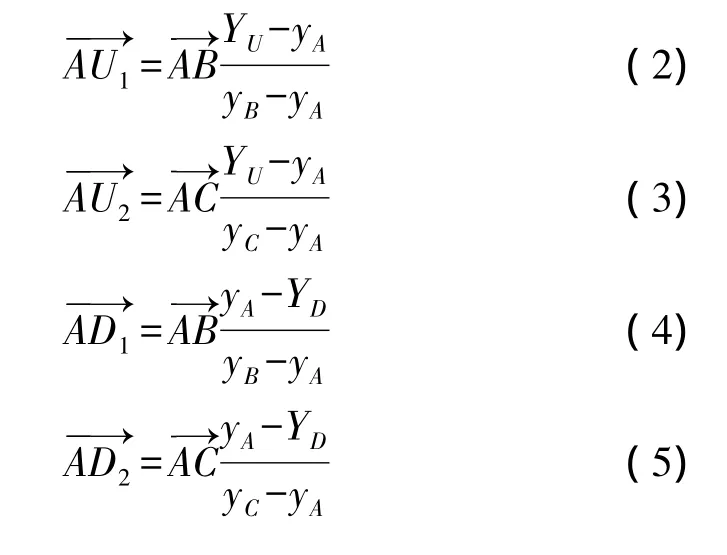
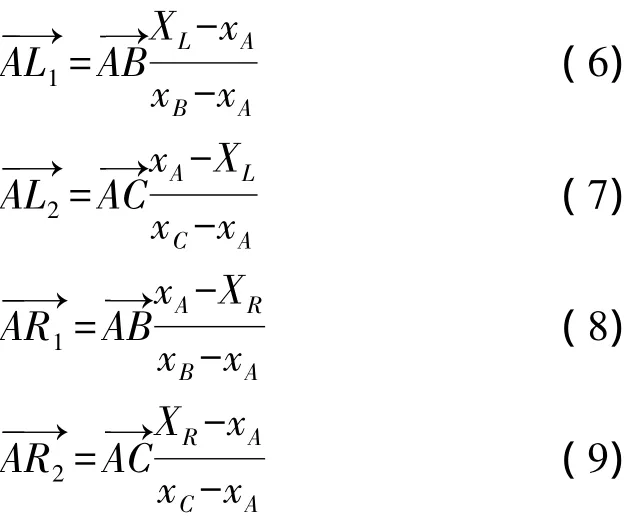
由于8个点(U1,U2,L1,L2,D1,D2,R1和R2)的坐标确定了模板的4条边: a,b,c,d,因此可以确定模板的轮廓。同理,将目标图像中与之对应的8个点设为:,根据仿射关系,则可以通过对应8个点的坐标确定目标区域的轮廓。
如图3所示,从目标图像的重心坐标序列中选取与A、B、C 3点对应的3个重心点: A'(xA',yA'),B'(xB',yB'),C'(xC',yC')。根据模板与目标图像的仿射关系,8个向量分别满足下列公式:
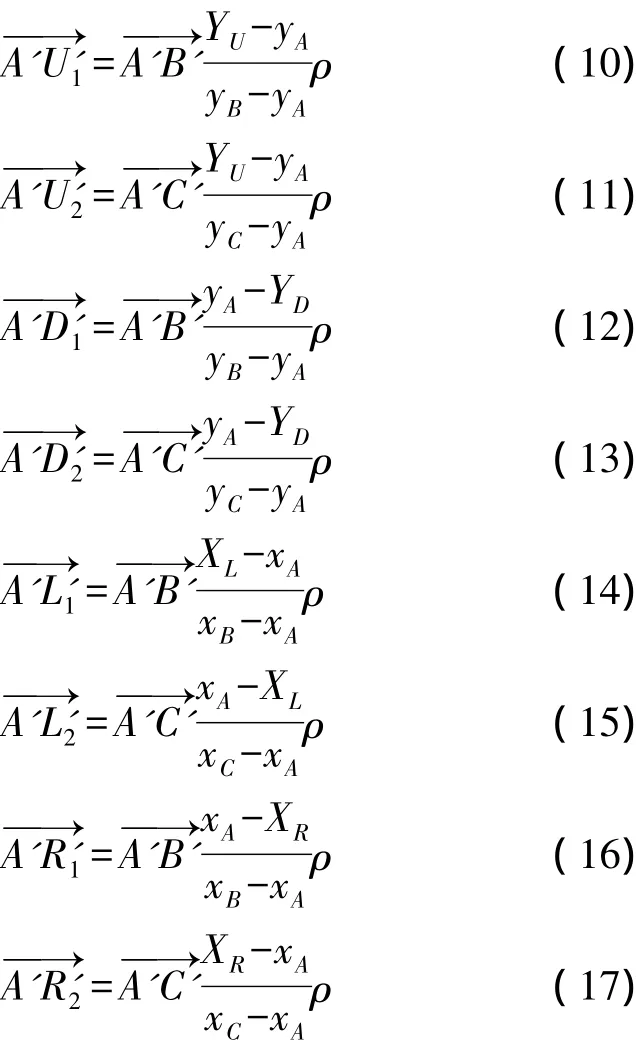
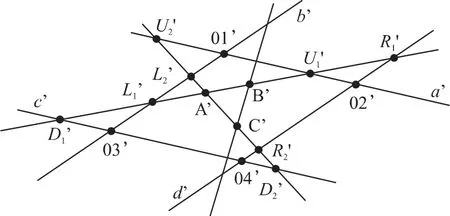
图3 目标图像几何图
在上述公式中,修正因子ρ∈[1,∞)。在实际应用中,离散的数据源会引入计算误差;成像透视变形会导致特征点对应的比例失真;同时,其他的因素也会带来一定的误差。这些误差会导致对目标区域定位的非完整性。引入修正因子ρ后,可适当调整选取范围,以完整定位目标区域。通过以上8个公式,可以计算得到8个点()的坐标,从而确定目标区域的4条边: a',b',c',d',进而确定目标区域的轮廓:
2.3交通标志ROI提取
3 交通标志的识别
模板与目标图像的ASIFT特征匹配确定了ROI所含交通标志的集合信息。在集合范围内,进一步识别ROI所含交通标志的具体类型。
3.1ROI特征点检测
在尺度空间[8]上,图像数据包含了图像自身的多尺度特征[9]。根据文献[10]提出的方法,利用高斯卷积核,可将二维图像I(x,y)的尺度空间描述如下[10-12]:
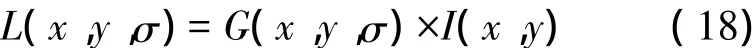
尺度可变高斯函数G(x,y,σ)定义如下[10-12]:
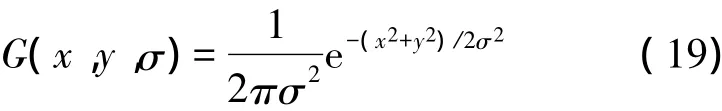
高斯差分尺度空间[13](DOG Scale Space)利用高斯差分核与图像进行卷积生成,DOG算子的定义如下所示[10-12]:
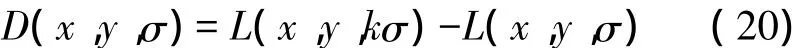
利用DOG算子将ROI图像的采样点和其相邻点比较,如果该点是邻域中的极值点,则将其判断为一个特征点。
3.2生成特征点描述
在ROI的特征点中,对每个特征点邻域窗口的梯度分布建立直方图统计,选取直方图峰值的梯度方向作为该特征点的主方向。将坐标轴旋转至主方向,以保证特征向量的旋转不变性。以特征点为中心选取16×16窗口,建立8个梯度方向的直方图。将16×16窗口分为16个4×4小块,在每个4×4小块上,标定每个梯度方向的累加值,形成一个种子点。这样一个特征点包含了16个种子点,每个种子点含有8个方向的向量信息。因此,每个特征点可以描述为一个128维的特征向量,该特征向量包含了邻域方向性信息,既增强了抗噪声能力,又对定位误差提供了较好的容错性[3]。
3.3特征向量匹配
将ROI所包含的图像记作Isrc,将ROI对应集合中的任意一幅交通标志图像记作Idst,计算Isrc特征向量与Idst特征向量的欧式距离[14],将欧氏距离的大小作为特征点相似性的判定度量[15]。方法如下:
选取Isrc中的一个特征点,记作点M,在Idst中找出与点M特征向量欧氏距离最近的两个特征点,最近特征点记作点T,次近特征点记作点R。计算点T与点R特征向量欧氏距离的比值,若比值小于一定的阈值,则认为点M与点T匹配成功[16]。阈值的大小与匹配个数正相关,与匹配稳定性负相关。根据最终的匹配结果,选取集合中匹配个数最多的交通标志图像作为最终的识别结果。
4 实验结果及算法性能分析
本节将围绕上述算法进行实验测试,并根据实验结果分析上述算法的识别性能。
实验平台的系统配置为: Windows 7操作系统和Intel Core i3-2310M处理器。在VS2010开发环境下,实现并测试了本文中提出的交通标志定位与识别方法。
4.1测试目标选择
为了证明上述算法具有适应光照,噪声和旋转变化的鲁棒性,被测试目标图像的取材条件为:光照条件下拍摄,交通标志与周围环境轻微融合,拍摄视角倾斜。如图4所示。

图4 测试目标图像
4.2模板匹配和集合确定
如图5所示,从左至右,从上至下,分别为模板bm1、bm4、bm5、bm10与目标图像的ASIFT特征匹配结果。从匹配结果可知,匹配程度最好的模板为bm1。

图5 模板与目标匹配
4.3交通标志ROI定位与提取
根据2.2和2.3中的定位与提取方法,确定的3个非共线重心点如图6(a)所示。修正因子取值1.2时,提取的交通标志ROI如图6(b)所示。图6(b)中,ROI的轮廓是掩码边界框与图像边界取交集的结果。
4.4交通标志识别
根据3.3中的方法,在最佳模板bm1相关集合范围内,匹配ROI与交通标志图像的特征向量。由于特征向量匹配涉及的数据量非常大,因此用ROI与交通标志图像的特征点匹配来演示最终的识别效果。如图7所示,从左至右,从上至下,分别为模板bm1集合中bm1_1、bm1_2、bm1_3、bm1_4与ROI的特征点识别结果。从识别效果中可以判断,目标图像中含有的交通标志为bm1_1所表示的交通标志,即禁止机动车通行标志。

图6

图7 交通标志识别结果
4.5算法性能分析
为了进一步证明该算法在实际应用中的可行性,在红色禁令标志,蓝色指示标志和黄色警告标志中,随机选取30种交通标志,并对其从不同角度拍摄取材进行实验。将标志平面与相机光轴的夹角记作θ,拍摄角度θ的范围为: 5°到175°,每隔5°拍摄一张,最后收集1 050张测试图像。用经典的LDA (Linear Discriminant Analysis)算法和本文中的算法同时对1 050张测试图像进行识别,识别结果如表1和表2所示。

表1 两种算法总体性能对比
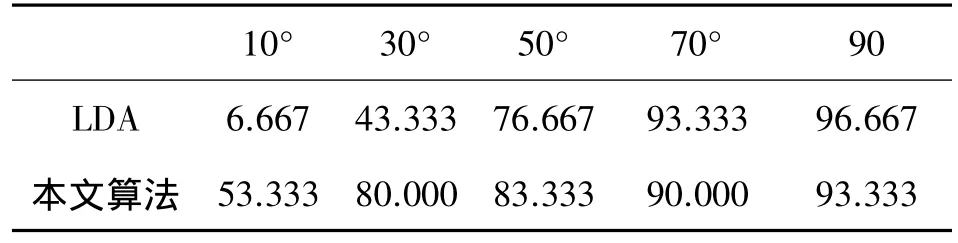
表2 两种算法对不同角度图像的识别率 单位: %
分析表1和表2可以得出如下结论:本文算法的总体识别率高于LDA算法,并且对图像角度的变化适应性较强。但是,本文算法的不足之处是识别时间较长,这是由ASIFT算法中多个仿射变换匹配引起的,导致算法的时间复杂度大于LDA算法。在空间复杂度上,由于研究目的倾向于识别率的提高,所以采用128维的特征向量来描述一个特征点,产生了较大的空间复杂度。实际应用时,可对空间复杂度和识别率折衷选择。借助专用数字信号处理器,可以在满足识别率的同时,优化该算法的时间和空间复杂度,从而实现该算法的实际应用。
5 结束语
本文通过分析ASIFT算法的特点,提出了一种基于ASIFT算法的交通标志定位与识别方法,并通过VS2010开发环境验证了该方法的可行性。通过实验结果可以得出,该方法在一定程度上克服了光照,噪声以及视觉条件的影响,达到了较好的定位与识别效果。在下一步的研究中,将结合DSP硬件平台,对该方法中涉及的关键环节进行优化,以降低时间和空间复杂度,从而实现该方法在嵌入式领域的实时应用。
参考文献:
[1]李祥熙,张航.交通标志识别研究综述[J].公路交通科技应用技术版,2010(6) : 253-257.
[2]Morel J M,Yu G.ASIFT: A New Framework for Fully Affine Invariant Image Comparison[J].SIAM Journal on Imaging Sciences,2009,2(2) : 438-469.
[3]Lowe D G.Distinctive Image Features from Scale-Invariant Keypoints [J].International Journal of Computer Vision,2004,60(2) :91-110.
[4]郑永斌,黄新生,丰松江.SIFT和旋转不变LBP相结合的图像匹配算法[J].计算机辅助设计与图形学学报,2010,2(2) : 286-292.
[5]蒋庆斌,王浩,赵力.基于UKF与SIFT的车辆跟踪算法研究[J].计算机测量与控制,2012,20(10) : 2824-2826.
[6]王鹏宇.基于小波和色彩传递夜视图像彩色融合算法研究[J].电子器件,2014,37(1) : 143-145.
[7]刘欢,郝矿荣,丁永生,等.光照鲁棒的抗模糊新组合不变矩图像匹配方法[J].传感技术学报,2013,26(9) : 1258-1264.
[8]傅卫平,秦川,刘佳,等.基于SIFT算法的图像目标匹配与定位[J].仪器仪表学报,2011,32(1) : 163-169.
[9]温文雅.一种改进的Harris多尺度角点检测算法[J].重庆理工大学学报,2012,26(8) : 94-97.
[10]陈杏环,闫海煜.基于随机游走策略改进的降雪模型图像分割方法[J].电子器件,2014,37(2) : 350-354.
[11]高绍雷,沈建新,周洪亚,等.高斯核函数在角膜地形图仪图像处理中的应用[J].小型微型计算机系统,2011,32(10) : 2074-2077.
[12]田莹,徐超,张一鸣.基于Gabor小波和ASIFT特征点的人耳识别[J].计算机应用与软件,2013,30(11) : 202-205.
[13]张良,王海丽,吴仁彪.基于改进局部不变特征的兴趣点匹配[J].电子与信息学报,2009,31(11) : 2620-2625.
[14]周强,杨智勇,孙小燕,等.基于图像欧式距离的KPCA SAR图像目标识别算法[J].火力与指挥控制,2012,37(12) : 38-41.
[15]张闯,王婷婷,孙东娇,等.基于欧式距离图的图像边缘检测[J].中国图象图形学报,2013,18(2) : 176-183.
[16]唐朝伟,肖健,邵艳清,等.全局结构化SIFT描述子在图像匹配中的应用[J].华中科技大学学报:自然科学版,2012,40(1) : 15-20.

焦再强(1989-),男,汉族,山西临汾人,太原理工大学硕士研究生,主要研究方向为信息处理与微系统,jiaozaiqiang@ foxmail.com;

李孟春(1963-),女,汉族,山西太原人,太原理工大学教师,副教授,硕士生导师,主要研究方向为光电技术,limmc163@ 163.com。
An Algorithm of Fast Video Block Motion Estimation
Based on Sub-GCK*
WANG Guan1*,LUO Shen1,GE Jia2
(1.The 28th Research Institude of China Electronics Technology Group Corporation,Nanjing 210007,China; 2.Laboratory of Image Science and Technology,Southeast University,Nanjing 210096,China)
Abstract:Fast video block motion estimation is one of the most important problems in video coding.Based on Gray Code Kernels(GCK) algorithm,the paper proposes an improved Sub Search Gray Code Kernels(Sub-GCK) algorithm,whose computational complexity reduces to 22.1% comparing to GCK.We also compare the encoding performance of new algorithms with that of GCK as well as some other common motion estimation algorithms in experiments.The results show that the proposed Sub-GCK algorithm,comparing to other ones,effectively reduces the time for motion estimation with guaranteed reasonable encoding quality.The running time of Sub-GCK algorithm is about 41.9% of original GCK algorithm.
Key words:video coding; motion estimation; sub search gray code kernels(Sub-GCK) ; computational complexity; running time
中图分类号:TP391
文献标识码:A
文章编号:1005-9490(2015) 03-0693-06
收稿日期:2014-07-01修改日期: 2014-07-11
doi:EEACC: 6120B10.3969/j.issn.1005-9490.2015.03.045
