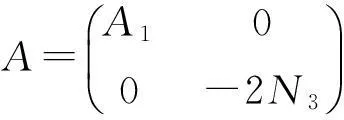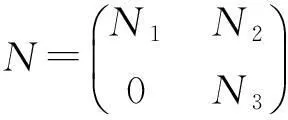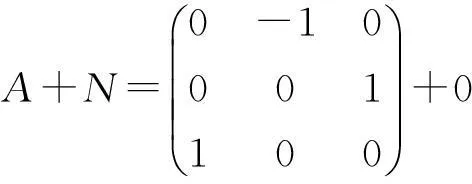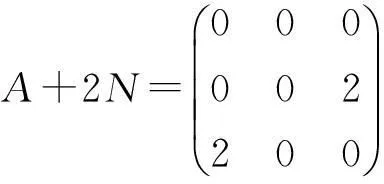一秩幂零算子的等价条件



一秩幂零算子的等价条件

张喆1,胡 海 祯2

(1.包头市北方重工第三中学, 内蒙古 包头 014030；2.包头市蒙古族中学, 内蒙古 包头 014030)

摘要：为进一步完善关于幂零算子的研究，本文给出阶数为一的幂零算子的等价条件，并给于证明.

关键词：Banach空间；幂零算子 ；矩阵表示

Bonsall and Rosenthal提出了幂零算子的模型问题, 许多学者在幂零算子方面进行了研究[1 - 2].本文主要研究阶数为一的幂零算子的等价条件.

用F表示实数域R或复数域C,F*=F{0}.设X是F上无限维的Banach空间.B(X)表示X上全体有界线性算子组成的算子代数.用Nk(X)及N(X)分别表示B(X)中所有阶数不超过k的幂零元的集合及所有幂零元的集合.对任意非零的x∈X,f∈X*,则由y|→x定义的算子是一秩的,通常记为x⊗f,并且B(X)中的每个一秩算子都可以写成这种形式.

定理设k≥3是一正整数，X为维数大于等于3的有限或无限维Banach空间,令N∈Nk(X)是一非零算子,则下列条件等价

(a)N∈N1(X)

(b) 对任意的A∈Nk(X),A+N∉Nk(X)蕴涵A+2N∉Nk(X).

证明："(a)⟹(b)" 设0≠N=x⊗f∈N1(X),Ak=0但(A+N)k≠0.如果A+N∉N(X),则由[3,Lemma2.1]([4]中引理6.4.1),我们有A+2N∉N(X),故(b)成立.因此下面可要求A+N∈N(X).取y∈X使得(A+N)ky≠0.容易看出,V=span{x,Ax,…,Ak-1x,y,Ay,…,Ak-1y}是A和N的公共不变子空间.令r为使得Arx=0的最小正整数.在V中取一组基{x,Ax,…,Ar-1x,e1,e2,…,em},则关于空间分解V=span{x,Ax,…,Ar-1x}⊕{e1,e2,…,em},A|V和N|V有矩阵表示

其中

由A+N∈Nk(X)可知a1=a2=…=ar-1=0.从而对每个正整数i≥0都有N|V(A|V)iN|V=0.进而,对任意的非零数α,我们有

(A|V+αN|V)k=α[N|V(A|V)k-1+A|VN|V(A|V)k-2+…+(A|V)k-1N|V]=α(A|V+N|V)k

所以(A|V+αN|V)ky=α(A|V+N|V)ky≠0,即(b)成立.

"(b)⟹(a)" 用反证法证明.假设(b)成立,但N∈Nk(X)不是一秩的.即rankN≥2,且对任意的A∈Nk(X),A+N∉Nk(X),蕴涵A+2N∉Nk(X).

首先讨论N2≠0,k≥4的情形.此时一定存在2

显然A∈Nk(X),A+N∉Nk(X)但A+2N∈Nk(X),矛盾.

当前一种情况发生时,我们令N的左上角6×6的矩阵块为N0,它所对应的X的子空间V0是N的不变子空间,即

〔参考文献〕

[1]C.-K.Li,P.Semrl,N.-K.Tsing,MapsPreservingtheNilpotentofProductsofOperators[J],LinearAlgebraAppl.2007,doi:0.1016/j.laa.2006.11.013.

[2]ZhaofangBai,JinchuanHou,LinearMapsandAdditiveMapsthatPreserveOperatorsAnnihilatedbyaPolynomial[J].J.Math.Anal.Appl.,2002,271:139-154.

[3]BaiZhaofang,HouJinchuan.AdditiveMapsPreservingNilpotentOperatorsorSpectralRadius[J],Acta.Math.Sinica.,2005,21(5):1 167-1 182.

[4]HouJ.C,CuiJ.IntroductiontolinearMapsonOperatorAlgebras[M].Beijing:SciencePress,2002.

The Equivalent Conditions of Rank one Nilpotent Operator

ZHANG Zhe1,HU Hai-zhen2

(1.Baotou North Hervy Industries No.3 Middle School, Baotou 014030

2.Baotou Mongolia National Middle School, Baotou 014030)

Abstract:For further improving the study of a nilpotent operator, this paper gives the order equivalent conditions of a nilpotent operator, and give the proof.

Key words:Banach space,；niloptent operator；matrix representation

中图分类号：O177

文献标识码：A

文章编号：1004-1869(2015)01-0020-03

作者简介：张喆(1978-)，内蒙古兴安盟人，研究方向：高中数学教育。

收稿日期：2014-11-04