两阶段链视角下河南省城市科技效率评价研究

张玉玲

（黄河水利职业技术学院，河南 开封 475004）

两阶段链视角下河南省城市科技效率评价研究

张玉玲

（黄河水利职业技术学院，河南 开封 475004）

建立两阶段链DEA模型，研究科技投入产出效率，由第一阶段科技创新和第二阶段科技应用组成。选取了2006～2013年共8年数据，对河南省城市科技投入产出进行评价分析，组成结果显示：（1）一些城市科技资源配置机制运行较差；（2）城市技术效率呈现以郑州为中心的偏高，其他城市较低，且其他城市与郑州市的科技效率差距较大。

河南省；城市建设；科技投入；技术效率；两阶段链DEA；结果与分析

0 引言

党的十八届三中全会通过的 《中共中央关于全面深化改革若干重大问题的决定》提出深化科技体制改革的战略决策，我国科技体制改革将迎来难得的机遇。近些年来，我国科学技术获得了迅猛发展，成果丰硕。但科技体制方面仍然存在一些弊端，束缚了科技生产力发展，制约着自主创新和科技支撑引领经济社会发展能力的提升。比如，科技与经济“两张皮”问题没有得到很好解决。当前我国经济正处于转型发展的关键时刻，提高经济的质量和效益，必须要以科技创新、技术进步为动力。技术创新支撑传统产业优化升级，科技更多地融入经济主战场。因此，一个科学合理、富有活力、更有效益的科技体制机制亟待建立，同时有效评价科技对经济的推动作用将具有更重要的实际意义。

本文采用两阶段链 DEA （Data Envelopment Analysis，DEA）评价方法，选取了2006到2013年共8年的数据，对河南省各城市科技投入产出进行评价研究，以使各城市认清自身在整个河南省中所处的位置，认识自身的优势和劣势，借鉴其他相对有效城市的成功经验，寻求提高自身科技效率的有效途径，为科技的管理和发展完善提供一些实践上可供参考的改进方向，同时为政府部门决策提供参考。

1 两阶段链DEA

1.1 研究方法概述

数据包络分析方法 （Data Envelopment Analysis，DEA）是由美国著名运筹学家A.Charnesh和W.W.cooper等人首先提出来的一种比较前沿效率评价方法［1～8］。此效率评价方法与传统的DEA仅考虑初始投入到最终产出的相对有效性所不同的是，链式DEA模型不但可以评价有链式结构的决策单元整体的有效性，而且可以评价各个阶段的有效性，从而可以发现具体哪个阶段存在“问题”，可以发现问题根本所在。此前学者把科技效率与科技应用效率分开研究，忽略了两者的内在联系。本文借用两阶段链式DEA系统模型，首先把二者根据具体样本数据进行整合，即，把科技投入产出效率分两个阶段：科技创新投入产出效率和科技应用投入产出效率。

两阶段链式DEA系统示意图如图1所示。第一阶段，X是子决策单元科技创新的投入／输入向量；Z1是其产出／输出向量。第二阶段，Z1和Z2是科技应用的投入／输入向量；Y是其产出／输出向量。

由于从科技创新到科技应用，从投入到产出之间在时间上存在一定的滞后性，因此本文在收集数据时，关于科技创新投入与科技创新产出及科技应用的投入与产出的计算，选择了第t年、第t＋1年和第t＋2年的数据。具体而言，科技创新投入指标采用2007年的数据，科技创新产出及科技应用的投入指标采用2008年的数据，而科技应用的产出则采用2009年的数据。因此，根据2006到2013年18个地市的数据，共得到108个样本。

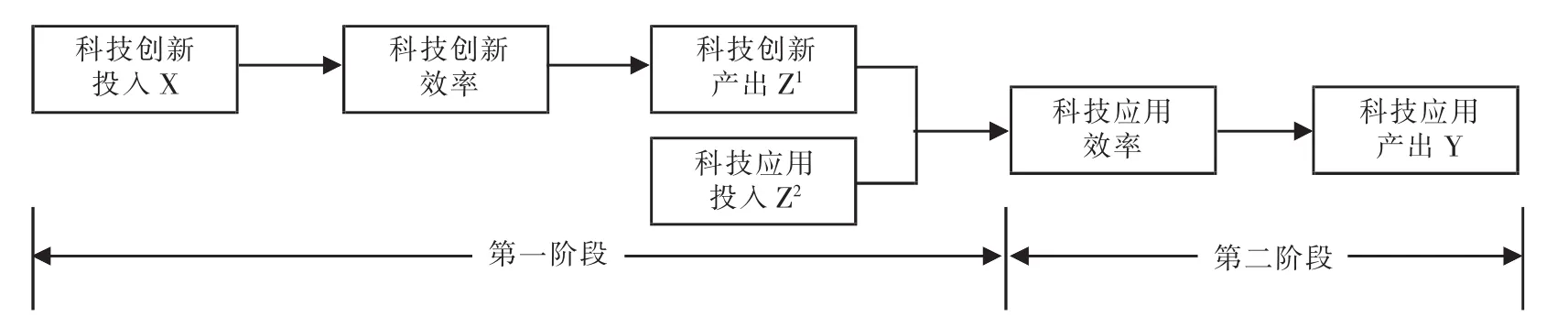
图1 科技投入产出效率评价的两阶段投入产出链Fig.1 Two-stage input and output series of science and technology input and output efficiency evaluation

1.2 两阶段链式DEA投入产出指标遴选

对各城市科技投入产出效率的影响因素非常之多，而且这些因素之间具有复杂的联系，因此，要想更好地体现出对城市科技投入产出效率进行对比和评价的效果，首先应该构建一套科学合理的投入产出评价指标体系。本文通过大量文献研究和实际调研［9～12］，根据科学性、合理性、可比性、可获得性等原则，深度结合当前河南省社会经济及科技发展趋势，来构建科技创新和科技应用投入产出因子，指标如下。

向量X中的指标有：科技活动人员，R＆D经费内部支出和R＆D经费外部支出。

向量Z1中的指标有：专利申请数，出版科技著作和技术成交量。

向量Z2中的指标有：地方财政科技拨款总额和科技活动人员。

向量Y中的指标有：GDP和城镇化水平。城镇化水平：指一个地区城镇化所达到的程度。城镇化指标系指城镇人口占总人口的比例，是世界各国衡量城镇化进展情况的最基本方法。GDP：是指在一定时期内（一个季度或一年），一个国家或地区的经济中所生产出的全部最终产品和劳务的价值，常被公认为衡量国家或地区经济状况的最佳指标。

根据以上指标，第一阶段中决策单元数量n＝108，输入指标数量m＝3，输出指标数量s＝3；第二阶段中决策单元数量n＝108，输入指标数量m＝5，输出指标数量s＝2；两阶段链模型中决策单元数量n＝108，外部的输入指标数量是5和输出指标数量是2，同时里面嵌套了第一阶段的输出和第二阶段的输入，总的输入指标数量m＝8和输出指标数量s＝5，均满足n≥3（m＋s）。

2 两阶段链式DEA模型构建

假设有J个决策单元，j为具体的决策单元，第一阶段每个决策单元有相同的投入M项，用Xmj（m＝ 1，2，…，M；j＝1，2，…，J）表示决策单元j的第m项投入。在第一阶段中，每个决策单元有相同的产出N项，用Z1nj（n＝1，2，…，N；j＝1，2，…，J）表示决策单元j的第n项产出。第二阶段的投入用向量Z＝（Z1，Z2）表示，其中Z1既是第一阶段的产出，又是第二阶段的投入；在第二阶段中，每个决策单元对应Z2投入部分有相同的投入P项，用Z2pj（p＝1，2，…，P；j＝1，2，…，J）表示决策单元j对应Z2投入部分的第P项产出；每个决策单元有相同的产出Q项，用Yqj（q＝1，2，…，Q；j＝1，2，…，J）表示决策单元j的第q项产出。另外，对应投入或产出的乘数用λ表示；整个C2R模型的效率用θ表示，C2R第一阶段和二阶段效率值分别用θ1和θ2表示［6］。

衡量第j0决策单元DEA是否有效，具体模型如下。

当仅考虑第一阶段时，其模型如下：

minθ1

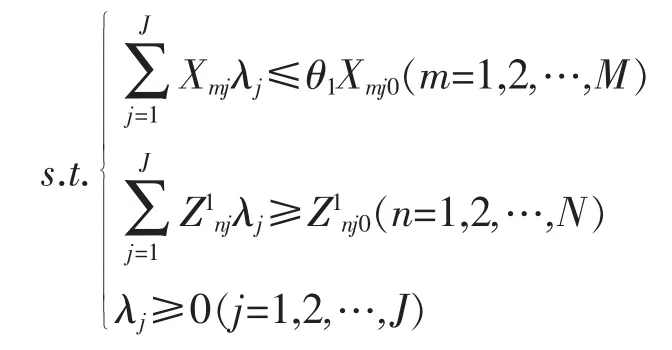
当仅考虑第二阶段时，其模型如下：

两阶段链模型如下：

minθ

3 实证结果与分析

依据两阶段链DEA系统模型，采用Matlab仿真系统软件，充分利用108个样本数据运算两阶段链DEA系统（上述3个模型）模型投入产出效率，结果如下。

3.1 三个模型运算结果分析

有效性分析：两阶段链、第一个阶段和第二阶段运算结果中DEA有效的单元数量分别是27、25和9，3个结果都满足有效单元数量小于决策单元总数量的1/3，说明3个模型均有效。

由于DEA分析获得的效率值是相对值，在同一个模型内各个决策单元具有可比性，在不同模型决策单元效率之间不具有可比性。这样可以采用不同城市不同时期效率值的排序对3个模型进行比较，对效率进行倒序排列，即效率越高，排序值越小。

依据两阶段链科技投入产出效率排序值，第一阶段科技创新和第二阶段科技应用效率排序值之间的关系分如下3类。

两阶段链排序值全部比第一阶段和第二阶段排序值大，表明该类城市科技资源配置机制运行较差。河南省一些城市在某年的科技效率较差情况如表1所示。表1列明了属于该类城市以及其对应的排序值，表中列明的样本时期采用科技创新产出的时间。具体来讲，2008年安阳市样本数据中，科技创新投入的数据是2007年的，科技创新产出和科技应用的投入数据是2008年的，而科技应用的产出数据是2009年的。表2也具有同样含义。从系统理论上来讲，此系统属于1＋1＜2的系统。这两个关联的分阶段运行子过程一起构成整体运行过程——两阶段链模型，这一整体过程不但要关注科技创新投入产出效率和科技应用的投入产出效率，同时还要关注运行过程中如何在前后两个过程中统一中间变量以获得最大的整体效率。虽然两个分阶段投入产出效率可能较好，但两个阶段融合起来也会出现整体效果较差的状况。

此两阶段链排序值位于第一阶段与第二阶段排序值之间，表明此类城市科技资源配置机制运行一般。从系统理论上来讲，这样的系统属于1＋1＝2的系统。采用比较第一阶段排序值和第二阶段排序值，从而找出排序相对靠后的阶段，进而有针对性地提高该阶段的效率，用以提高整体效率。

两阶段链排序值全部比第一阶段与第二阶段排序值都要小，表明此类城市科技资源配置机制运行效率较高。河南有一些城市在某年份科技效率较高情况如表2所示。表2列明了属于此类城市以及其相对应的排序值。从系统理论上来讲，这样的系统属于1＋1＞2的系统。贝塔朗菲总是强调，任何系统都是一个有机的整体，它不是各个部分的机械组合或简单相加，系统的整体性功能是各要素在孤立状态下所没有的新质［13］。因此，此类城市在充分保障经济社会发展的同时采取科技支撑战略的理念实施科技创新，达到了“整体大于部分之和”的良好效果。

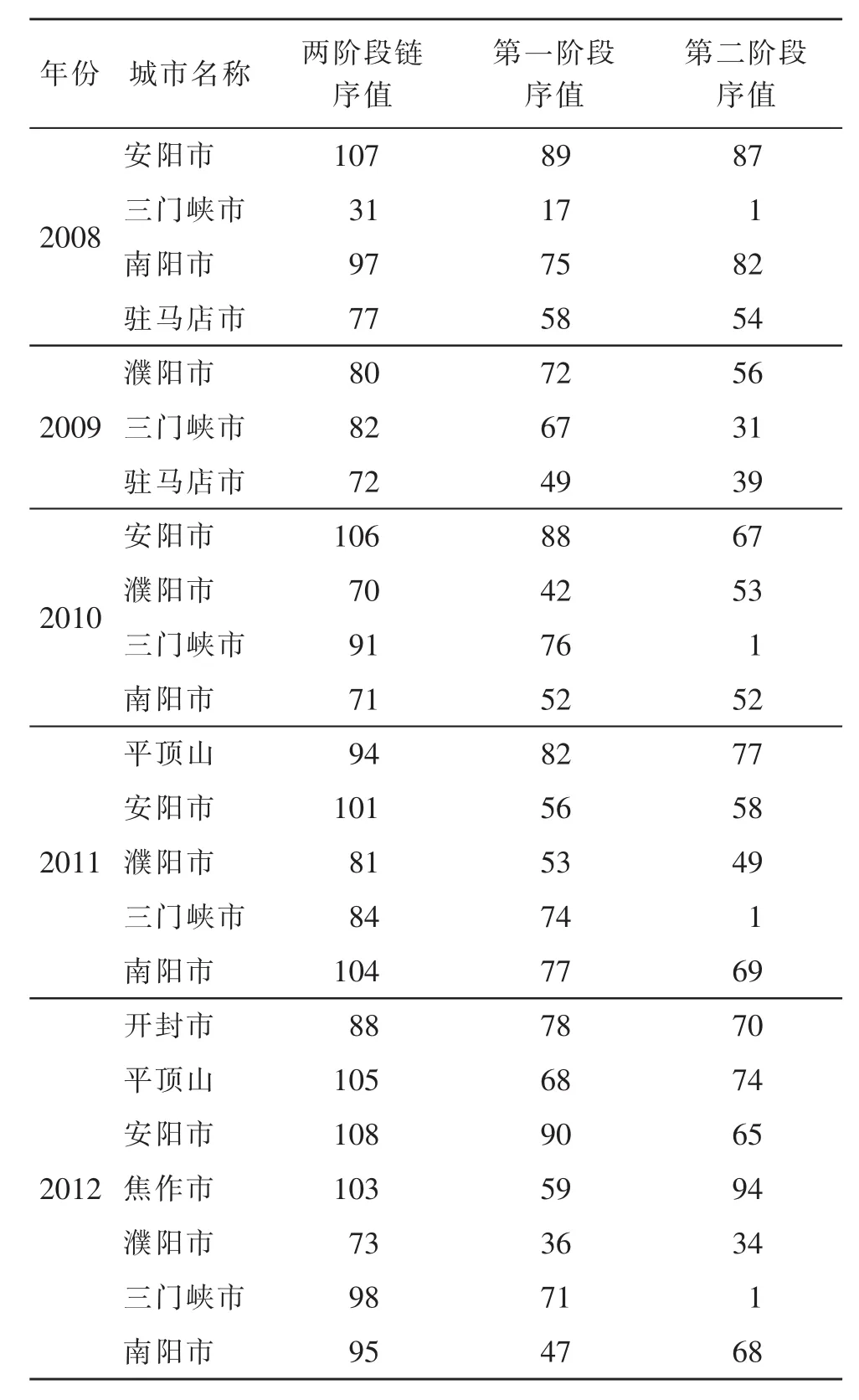
表1 两阶段链排序值均比第一阶段和第二阶段排序值大的样本Table 1 The sam ple of two-stage series rank value is greater than the first-stage and the second-stage’value

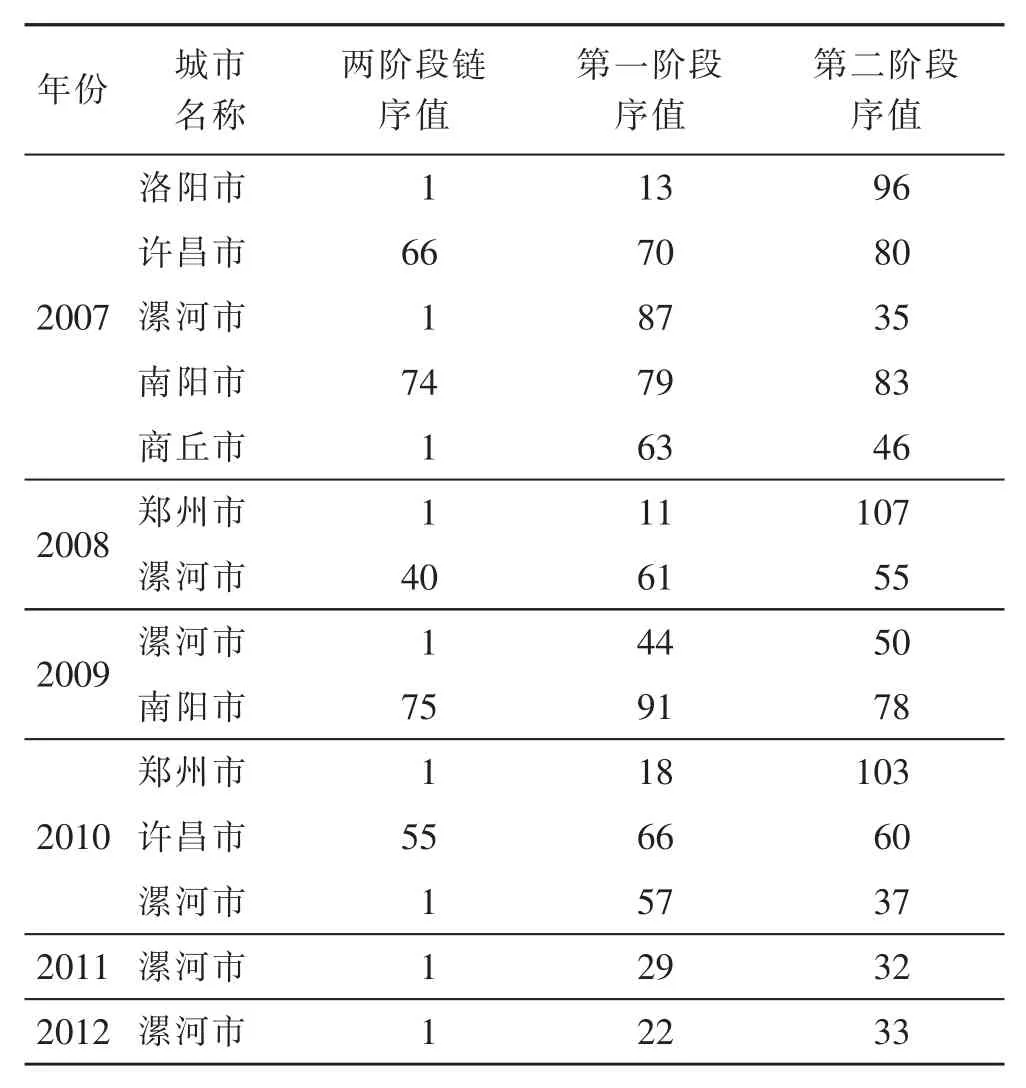
表2 两阶段链排序值均比第一阶段和第二阶段排序值小的样本Table 2 The sam ple of two-stage series rank value is less than the first-stage and the second-stage’value

3.2 不同城市之间科技效率的比较

2006～2013年河南省不同城市之间科技效率比较情况如图2所示。图2列明各城市不同时期的效率平均值，在科技效率大于0.8的标准要求下，只有郑州市和洛阳市，在所有城市中科技效率最小的两个城市分别是平顶山市和周口市，两市的效率分别为0.21和0.19。

在地理范围上以郑州为中心的城市群的科技效率分别是：洛阳市科技效率为0.85、焦作市科技效率为0.58、新乡市科技效率为0.59、开封市科技效率为0.68和许昌市科技效率为0.55，仅有洛阳市的科技效率超过了0.8，而其他城市的科技效率均相对较低，表明省会郑州市的辐射能力不强。除了郑州附近的城市群，其他地区城市，无论东南部城市还是西北部城市，科技效率均相对更低。总体上而言，河南省各城市科技效率呈现：以省会郑州市为中心的中部城市科技效率相对偏高，而其他城市都相对较低。河南省18个地市的科技效率以省会郑州市最好为0.94，其他地市最好的仅仅为0.85，最差的仅有0.19，此情况就是表明河南省其他城市与省会郑州市的科技效率差距非常明显。从18个地市所处的地理位置来看，省会郑州市是河南省的政治、经济、文化中心，所以各方面的资源优势都相对较强，科技效率最好也在情理之中；而科技效率较低的那些地市都是处在河南省的边远地区或者山区，这些地区的资源优势相对较弱。

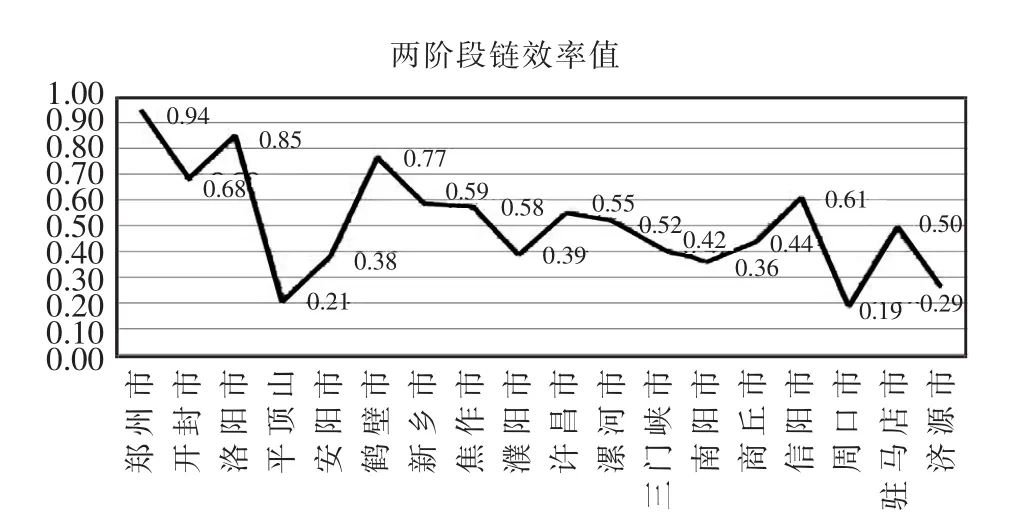
图2 河南省2006～2013年各城市科技效率均值Fig.2 Every city efficiency mean value in Henan province from 2006～2013

4 结论

本文利用两阶段链DEA模型研究科技投入产出效率，该模型嵌入了第一阶段科技创新投入产出效率和第二阶段科技应用投入产出效率。选取了2006到2013年共8年数据，对河南省各城市科技投入产出进行评价研究，结果如下：（1）从系统理论分析，两阶段链排序值均比第一阶段和第二阶段排序值大的样本数23个，两阶段链排序值均比第一阶段和第二阶段排序值小的样本数14个，说明更多的城市科技资源配置机制运行较差；（2）总体上，河南各城市科技情况效率呈现为以郑州为中心的中部城市技术效率偏高，其他城市较低，且其他城市与郑州市的科技效率差距较大。

［1］Banker R D，Charnes A，Cooper W W.Some models for estimating technical and scale inefficiencies in date envelopment analysis ［J］.Management science，1984，30（9）：1078－1092.

［2］Cooper W W，Seiford L M and Tone K.Data envelopment analysis：A comprehensive text w ith models［M］.Applications，references and DEA－solver，Kluwer academ ic publishers，Boston.2000.

［3］Zhong W，Yuan W，Li S X，et al.The performance evaluation of regional R＆D investments in China：An application of DEA based on the first official China e-conom ic census data［J］.Omega，2010（39）：447－455.

［4］Banker R D，Natarajan R.Evaluating contextual variables affecting productivity using data envelopment analysis［J］.Operations Research，2008（56）：48－58.

［5］Guan JC，Chen K H.Measuring the innovation production process： A cross－region empirical study of China＇s high－tech innovations［J］.Technovation，2010（30）：348－358.

［6］孙建军，程慧平，董刚.基于三阶段DEA模型的信息产业效率研究［J］.情报学报，2012，31（8）：875－882.

［7］黄神，葛虹，冯英浚.基于链形系统的关联网络DEA模型：以我国14家商业银行为例［J］.系统工程理论与实践，2009，29（5）：106－114.

［8］闫庆友，陶杰，姚鑫.利用旋转算法构建DEA模型生产前沿面［J］.系统工程理论与实践，2014，34（1）：94－103.

［9］刘绘珍.国家中心城市科技投入产出效率评价——基于五大中心城市的数据［J］.郑州航空工业管理学院学报，2013，31（5）：81－84.

［10］张巍，高汝熹.科技创新实力和效率的比较研究——基于科学发现和技术创新的二维视角 ［J］.科技与经济，2013，26（6）：21－25.

［12］李庆华.区域科技创新效率演化与影子价格研究［J］.科技进步与对策，2014，31（15）：35－39.

［13］（美）冯 贝塔朗菲.一般系统论基础、发展和应用 ［M］.林康义，魏宏森译.北京：北京清华大学社，1987：56－189.

[责任编辑 樊建科]

Research on City Science and Technology Efficiency Evaluation in Henan Province at the View of Two-stage Series

ZHANG Yu-ling
(Yellow River Conservancy Technical Institute,Kaifeng 475004,Henan,China)

It establishes two-stage series DEA model,researches science and technology input and output efficiency,the first-stage science and technology innovation and second-stage science and technology application.By selecting the 8 years data from 2006-2013,it evaluates and analyzes the city science and technology input and output in Henan province.The result shows: (1)some cities’science and technology resource allocation mechanism are weak;(2)Zhengzhou city technology efficiency is better than other cities.

Henan province;city construction;science and technology input;technology efficiency;twostage series DEA;result and analysis

F13/2.43

A

1008-486X（2015）02-0095-05

2014-12-25

河南省教育厅人文社会科学研究项目：两阶段链视角下河南省城市科技效率评价研究（2014-QN-072）；河南省政府决策研究招标课题：加快河南省由工业大省向工业强省跨越的研究（2014152）。

张玉玲（1980-），女，河南尉氏人，讲师，硕士，主要从事高校物流管理的教学与研究工作，工作方向：物流管理。