基于SolidworksM otion的内燃机活塞运动规律分析
2015-02-25连萌,江斌,李冰
连 萌,江 斌,李 冰
(黄河水利职业技术学院,河南 开封 475004)
基于SolidworksM otion的内燃机活塞运动规律分析
连 萌,江 斌,李 冰
(黄河水利职业技术学院,河南 开封 475004)
内燃机曲轴的转动一般是均匀的。因为活塞连杆的运动伴随着较大的加、减速度,对受力构件的强度、耐久性影响很大,易导致振动和噪声,所以有必要对其运动规律和特性进行研究。利用Solidworks M otion对活塞连杆机构的运动情况进行了仿真模拟,近似方程曲线对比,分析了活塞连杆机构的运动规律。
内燃机曲轴;运动仿真;运动分析;Solidworks Motion软件;Mathematics软件
0 引言
往复活塞式内燃机的特征之一是工作不均匀。这主要是因为,内燃机活塞连杆组的运动伴随着极大的加、减速度,产生超重1 000~2 000倍的惯性载荷,对受力件的强度、耐久性影响很大,可能导致振动和噪声[1]。近年来,为了提高内燃机的比功率,减小质量和尺寸,内燃机的转速越来越高。因此,运动学研究更加显得重要。本文在Solidworks中建立曲轴活塞模型,进行运动仿真,对比由近似方程得出的位移、速度、加速度曲线,对中心曲柄连杆机构活塞的运动规律进行了分析。
1 中心曲柄连杆机构的运动规律和方程
中心曲柄连杆机构的特点是,气缸中心线通过曲轴的旋转中心,并垂直于曲轴的回转轴线。这种形式的曲柄连杆机构在内燃机中应用最为广泛。一般的单列式内燃机,采用并列连杆与叉形连杆的V形内燃机,以及对置活塞式内燃机的曲柄连杆机构都属于这一类。
1.1 中心曲柄连杆机构的运动规律
曲轴的运动规律可近似视为作等角速度的回转。这样的假定对近代的多缸高速内燃机来说是允许的。因为内燃机在稳定工况下工作时,由于扭矩不均匀性而引起的曲柄回转角速度变化不大[2]。
图1是中心曲柄连杆机构运动分析简图。图中,气缸中心线通过曲轴中心O,OB为曲柄,AB为连杆,B为曲柄销中心,A为连杆小头孔中心或活塞销中心。曲轴转角α是从气缸轴线顺着曲轴转动方向度量。当α=0°时,对应的A′表示活塞运行到上止点位置。当α=180°时,对应的A″表示活塞运行到下止点位置。
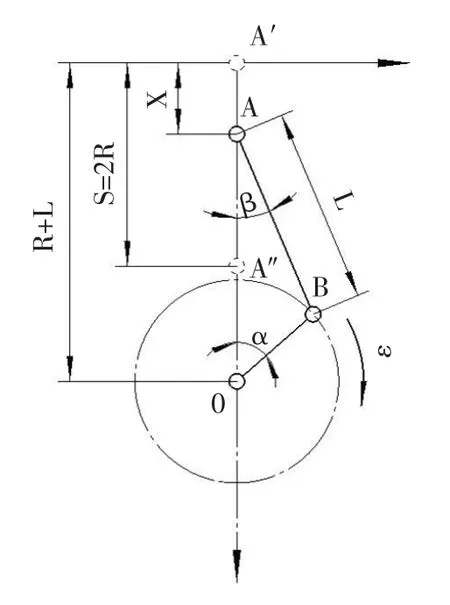
图1 曲柄连杆机构简图Fig.1 Crankshaft and connecting rod mechanism
当曲柄做等角速度ω旋转时,曲柄OB上任意一点都以O点为圆心,作等速旋转运动;A点(即活塞)沿气缸中心线作往复直线运动;连杆AB作复合的平面运动,其大头与曲柄销(即B点)的运动一样,作等速的旋转运动,小头与活塞一样作往复运动。所以,连杆本身的运动是由旋转运动和往复运动合成的平面复合运动。在实际分析中,为使问题简化,一般将连杆简化为分别集中于连杆大头和小头的两个集中质量,认为它们分别作旋转与往复运动。这样,就不需要对连杆的运动规律进行单独的研究。
活塞在作往复运动时,其速度和加速度是变化的。它的速度和加速度的数值及变化规律对曲柄连杆机构以及内燃机整体的工作有很大的影响。因此,研究曲柄连杆机构运动学的主要任务就是研究活塞的运动规律。
1.2 曲柄连杆机构的运动方程
如果曲柄半径OB的长度为R,连杆AB的长度为L,曲柄半径与连杆长度的比值为λ,即λ=R/L。由图1可知,
x=A′A=A′O-AO=R+L-(l cosβ+R cosα)。
在△AOB中,利用正弦定理有

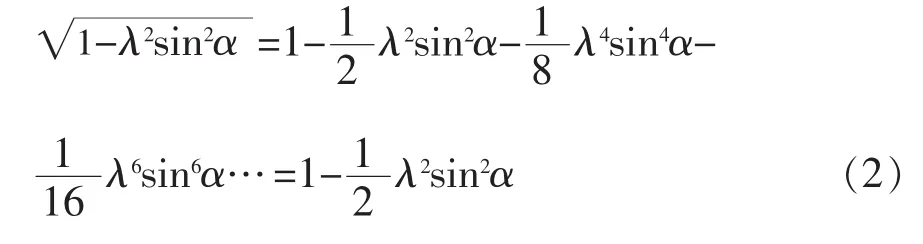
将公式(2)代入公式(1)可得
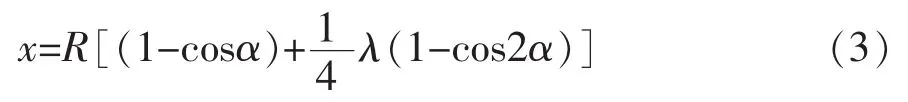
公式(3)为活塞的位移近似方程。
将式公(3)对时间t求导,可得活塞速度的近似方程,即

将式(4)对时间t求导,可得加速度a的近似表达式,即

2 活塞模型的运动仿真和分析[3~6]
在S olidworks中,创建曲柄活塞的三维模型,进行装配。然后,在Solidworks Motion中,为曲轴添加“旋转马达”,使曲轴绕轴线转动,如图2所示。在创建模型时,因为把活塞竖直放置,活塞移动方向为z轴方向,故取活塞的位移曲线如图3所示。为了便于分析,以活塞位于上止点的时刻为分析起点,转动一周,持续时间为4 s(周期T=4 s)。所以,曲线中1 s处为T/4,对应曲轴转角90°;2 s处为T/2,对应曲轴转角180°;3 s处为3T/4,对应曲轴转角270°;4 s处为T,对应曲轴转角360°。
将活塞的位移近似方程用Mathematics绘制出方程曲线,如图4所示。对比两条曲线可以看到,曲线的变化情况完全一致。

图2 活塞、曲轴结构Fig.2 M odels of piston and crankshaft
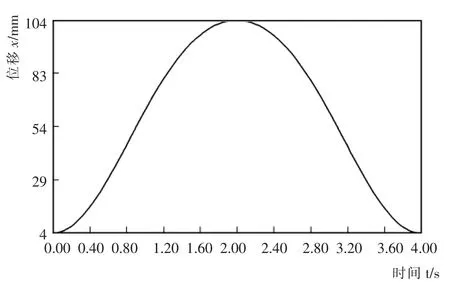
图3 在S olidworks M otion中得到的位移曲线Fig.3 Displacement curve of S olidworks M otion
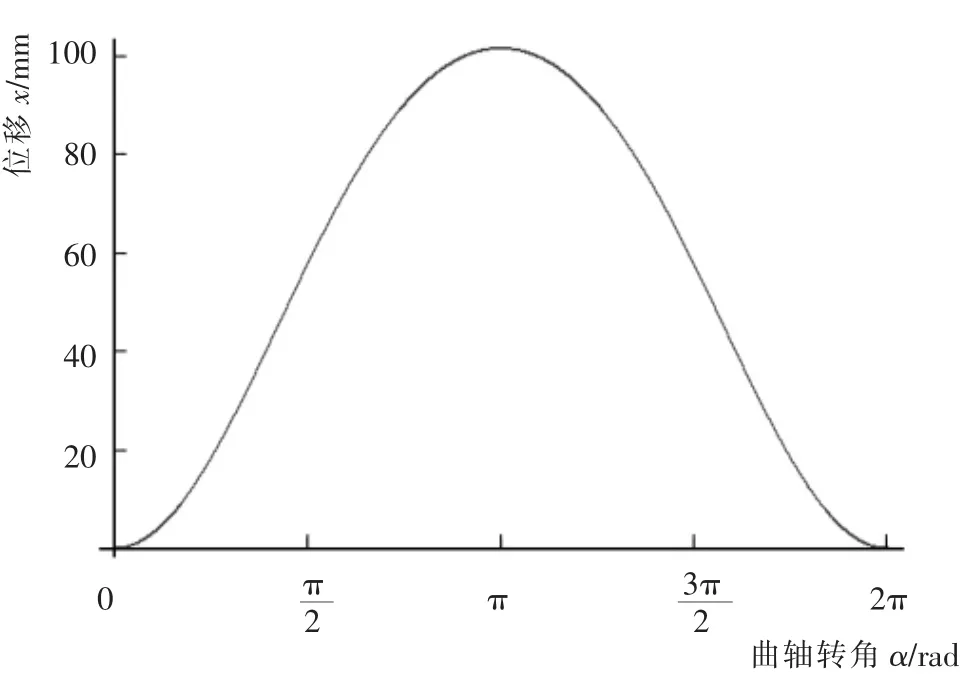
图4 由近似方程得到的位移曲线Fig.4 Displacement curve of approximate equation
2.1 位移分析
2.2 速度分析
由Solidwork M otion所得的活塞速度曲线如图5所示,图6为Mathematics按式(4)绘制的曲线。由图5和图6可知,活塞的速度近似方程和仿真结果完全吻合。α=0~180°时,为活塞由上止点向下止点运动过程,速度v为正值,对应图5中0~2 s的曲线;当α=180°~360°时,为活塞由下止点向上止点的运动过程,速度v为负值,对应图5中3~4 s的曲线。在α为0°、180°、360°时,v=0,活塞正在改变运动方向。由式(4)可知,α=90°、270°时,v=Rω,活塞速度等于曲柄销中心的圆周速度,并不是活塞最高速度(绝对值)vmax。活塞速度最大时的曲轴转角为αvmax,αvmax小于90°或大于270°,即活塞速度的最大值出现在偏向上止点的一边。Rωsin2α两个速度分量之和,所以活塞速度可视为由Rωsinα和
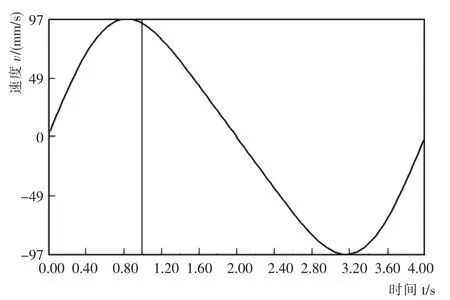
图5 由S olidworks M otion得到的速度曲线图Fig.5 Velocity curve of S olidworks M otion
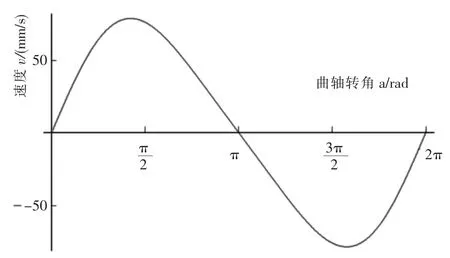
图6 由近似方程得到的速度曲线图Fig.6 Velocity curve of approximate equation
因为速度v可以看作Rωsinα和两部分简谐运动速度组成,如图7所示。

图7 速度曲线的合成图Fig.7 Speed curve
2.3 加速度的分析
由Solidwork M otion所得的活塞加速度曲线如图8所示,图9为Mathematics按式(5)绘制的曲线。由图8和图9可知,活塞的加速度近似方程和仿真结果也是完全吻合。式(5)也可以写作α=Rω2cosα+ λRω2cos2α,即活塞的加速度也可以认为是Rω2cosα和λRω2cos2α两个简谐运动加速度之和。活塞加速度的极值点(最大正加速度和最大负加速度)以及相应的曲轴转角α可用上式对α的微分并令其值等于0来求得,即,所以
sinα(1+4λcosα)=0。
可得,sinα=0或(1+4λcosα)=0。
当sinα=0时,加速度的极值点出现在α=0°和α=180°处,相应的加速度分别为:α=0°时,a=Rω2(1+ λ)、α=180°时,a=-Rω2(1-λ)。
综上所述,在曲轴旋转的一周中,当α=0°和360°时,有最大正向加速度,对应活塞通过上止点时刻。最大负向加速度的出现和曲柄半径与连杆长度的比值λ有关,当时,最大负向加速度出现在α=180°处;时,最大负向加速度出现在处,如图10所示。
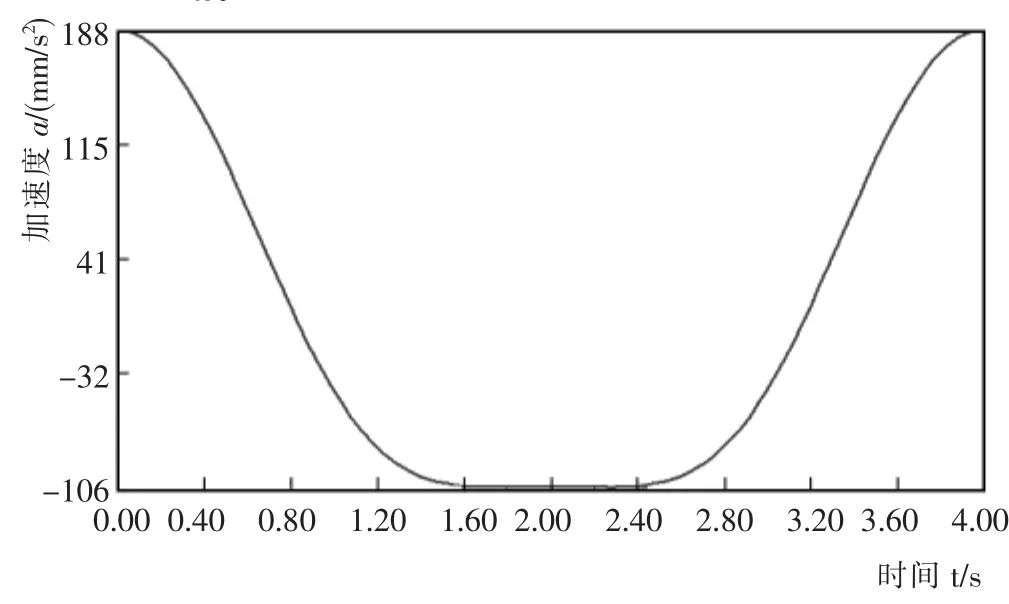
图8 由S olidworks M otion得到的加速度曲线Fig.8 Acceleration curve of S olidworks M otion
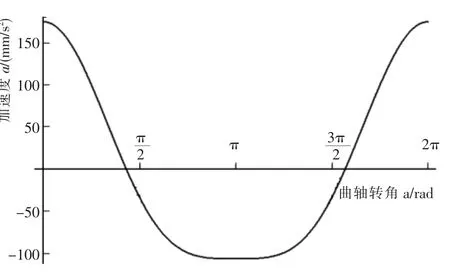
图9 由近似方程得到的加速度曲线Fig.9 Acceleration curve of approximate equation
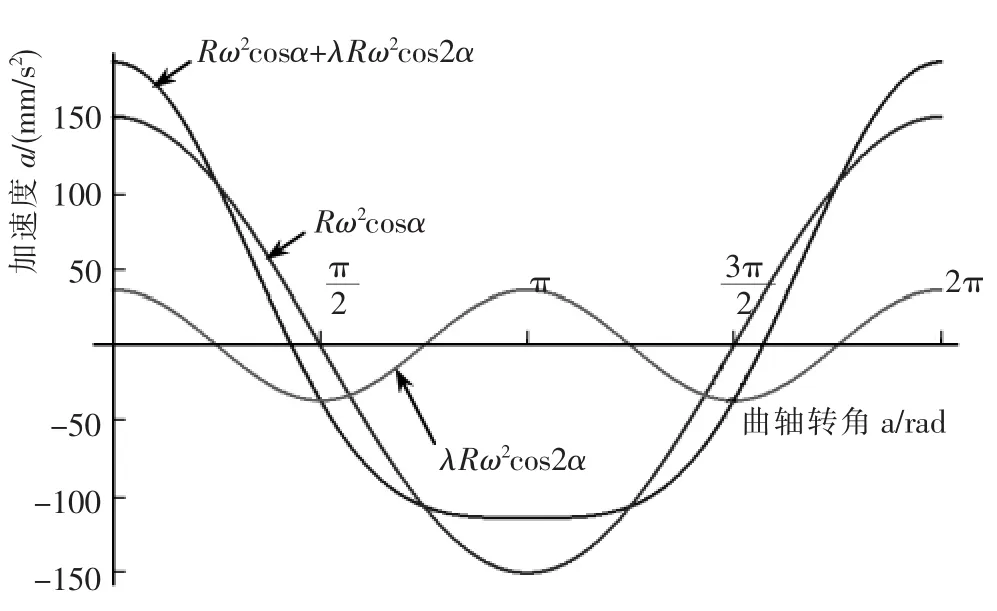
图10 加速度曲线的合成Fig.10 Acceleration curves
3 结语
本文通在Solidworks中建立了曲轴活塞模型,在Solidworks M otion中进行运动仿真,生成了活塞运动的位移曲线、速度曲线和加速度曲线,用Mathematics对位移、速度和加速度近似方程曲线进行绘制,将两组曲线进行对比,完全吻合,并对中心曲柄连杆机构活塞的运动规律进行了分析,为活塞运动时的受力分析奠定了基础。
[1]周宝龙.内燃机学[M].北京:机械工业出版社,1999:261-288.
[2]袁兆成.内燃机设计[M].北京:机械工业出版社,2008:58-68.
[3]卫江红.基于SolidW orks的连杆机构的运动分析与仿真[D].大连理工大学,2005:15-19.
[4]黄敬敏,林益丽.SolidW orks+motion+simulation建模机构结构综合实训教程[M].北京:清华大学出版社,2009:97-132.
[5]张晋西,郭学琴.SolidW orks及COSMOSMotion机械仿真设计[M].北京:清华大学出版社,2007:1-16.
[6]李大磊.赵玉奇.SolidWorks高级功能与工程应用[M].北京:北京邮电大学出版社,2009:133-185.
[责任编辑 杨明庆]
TK45
B
1008-486X(2015)02-0034-04
2014-07-10
连 萌(1982-)男,河南郑州人,硕士,讲师,主要从事工程机械的教学和科研工作。
