面向TD-LTE通信系统的功放新模型

南敬昌，李厚儒，方 杨

辽宁工程技术大学 电子与信息工程学院，辽宁 葫芦岛125105

1 引言

当今，无线数据宽带需求正在急剧增长，如何利用现有的TDD频谱资源来实现LTE产业规模效应的最大化，已经成为全球LTE产业的热点问题之一。而在我国，LTE技术快速发展，并且在部分地区已经开始商用。由于LTE采用了复杂的OFDM调制方式，使得整个系统对功放的线性度提出了更高的要求。线性度的提升要求功放具备更高的功率回退，使得功放工作在远离饱和区，从而达到在有限带宽内实现快速准确通信的目的。Doherty技术[1-3]在高的功率回退范围内能提高功放的效率，并且能够很好地结合数字预失真技术以实现高效率、高线性度功放的要求。而对于Doherty功放非线性特性[4]的预估，行为模型的结构建立与参数提取有着重要意义。

在射频领域中，对功率放大器和无线发射设备建模是非常有价值的研究方向。在过去的二十年里，各种参数化和非参数化模型被提出用来描述无线通信系统的静态非线性行为和动态记忆效应。Volterra级数[5-6]模型是已建立的综合模型，可模拟功放的静态和动态效应。然而其模型系数非常庞大，参数难于提取，计算复杂度相对较高。记忆多项式[7-8]为Volterra级数的简化形式，因其系数提取相对容易而被广泛应用于功放行为建模中。记忆多项式模型参数的提取可以直接利用最小二乘技术，除了辨识过程非常容易实现外，最突出的优势在于最小二乘法中代价函数只有一个最小值，即参数测定过程不会陷入局部极小。

然而，众所周知，在模型参数的提取过程中，输入变量的频率间隔略微变化将会导致记忆多项式模型遭遇灾难性的误差，这正是由于记忆多项式功放模型所存在的固有局限。因此，记忆多项式功放模型不适用于模拟大信号激励下的功放行为。

本文提出的有理函数模型是基于两个记忆多项式模型的比率，该模型的参数可以采用最小二乘法技术提取。当输入信号的幅值无限增加时，输出可以收敛到一个有限值。在模型的验证阶段，利用ADS软件设计了一款面向TD-LTE的晶体管级DPA电路模型，导出输入输出信号包络数据用于有理函数功放模型的建立和测试，结果表明，该模型能够模拟功放的记忆效应[9]，并且在模型参数数目相同的条件下，与记忆多项式模型相比减小了误差，提高了模拟精度。

2 模型分析

2.1 记忆多项式模型

基带功放记忆多项式模型的一般式可以表示为：

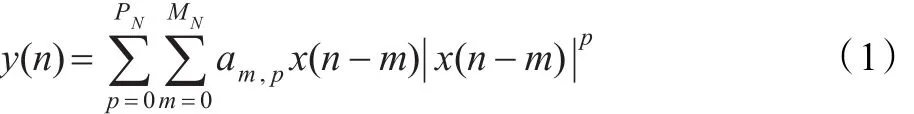
x(n)和y(n)分别是记忆多项式模型输入和计算的输出。am，p为记忆多项式的复系数。P表示模型的最大非线性阶数，M为记忆多项式模型的记忆阶数，故它们均是整数形式。

2.2 有理函数功放模型

（1）模型结构说明

与传统的记忆多项式结构不同，有理函数模型很少被涉及用于模拟功率放大器的行为。事实上，如文献[10]所述，有理函数模型可被化简为Saleh模型（以及Saleh函数的改进形式，如文献[11-12]所述）。本文给出了一个一般形式的有理函数模型，被定义为：

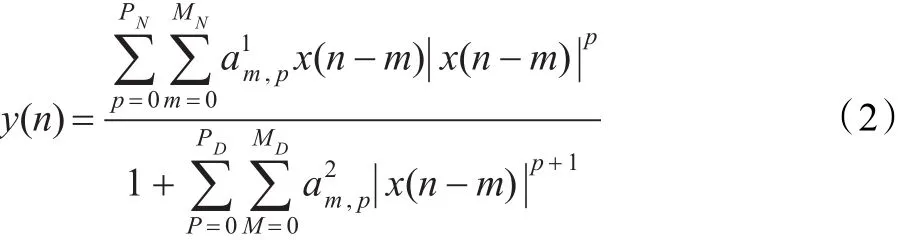
其中x(n)和y(n)分别为有理函数功放模型的输入和计算输出的时域信号样本。需要注意的是，公式（2）中的分母和分子都采用记忆多项式模型格式，和分别为两个记忆多项式模型的复系数，P和M分别为模型的最大非线性阶数和记忆深度。需要指出的是，在这里记忆多项式模型的扩展形式也可以被使用来代替记忆多项式模型，例如动态记忆多项式模型[13]和通用记忆多项式模型结构[14]。

控制有理函数模型的实验误差是相当重要的，这就需要分母和分子有相同的多项式非线性阶数，即PN=PD。事实上，满足这个条件就可以确保当x(n)的幅值无限增加时y(n)收敛到一个有限大信号幅值。

如表达式（2）所示，有理函数模型能够模拟功率放大器的大信号特性。分母的特殊形式使得模型能够区别描述大信号和小信号激励下的动态行为。当输入小信号驱动功放时，分母趋近于整数，这样小信号特性主要由分子决定（得到了与记忆多项式近似相同的模拟结果）。当输入信号的幅值增大，模型呈现出压缩趋势。分母仍包含记忆项，模型将呈现出不同于小信号条件的大信号动态行为。

（2）模型辨识说明

辨识有理函数功放模型的参数可以采用最小二乘技术。给出一组输入及输出信号数据，将表达式（2）改写成递归多项式模型形式，如公式（3）：

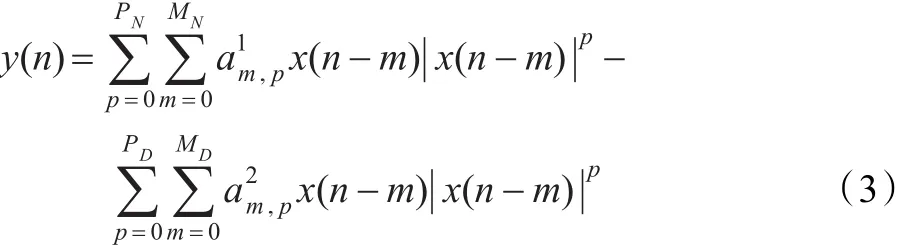
辨识过程如下：

首先令：

其中Y是有理函数模型的输出向量，X是由两个记忆多项式基函数组成的矩阵，A代表两个记忆多项式模型组成的模型参数向量。

X被定义如下：

其中Xa1，Xa2分别为利用两个多项式基函数构造的子矩阵。

利用最小二乘法[15-16]拟合，可求得到模型参数：

3 功放设计及参数提取

为用新的行为模型对功放建模，需在ADS环境下提取功率放大器的输入输出信号包络数据。本文结合互调对消技术和多谐波双向牵引技术，设计出了应用于工作频段为2.57～2.62 GHz的TD-LTE基站功率放大器。峰值输出功率210 W，要求在峰值功率回退10 dB处PAE＞45%，IMD3＜-25 dB，根据指标要求选用了NXP公司的BLF6G27-75和BLF6G27-135两款LDMOS管进行DPA电路匹配设计，电路原理图如图1所示。

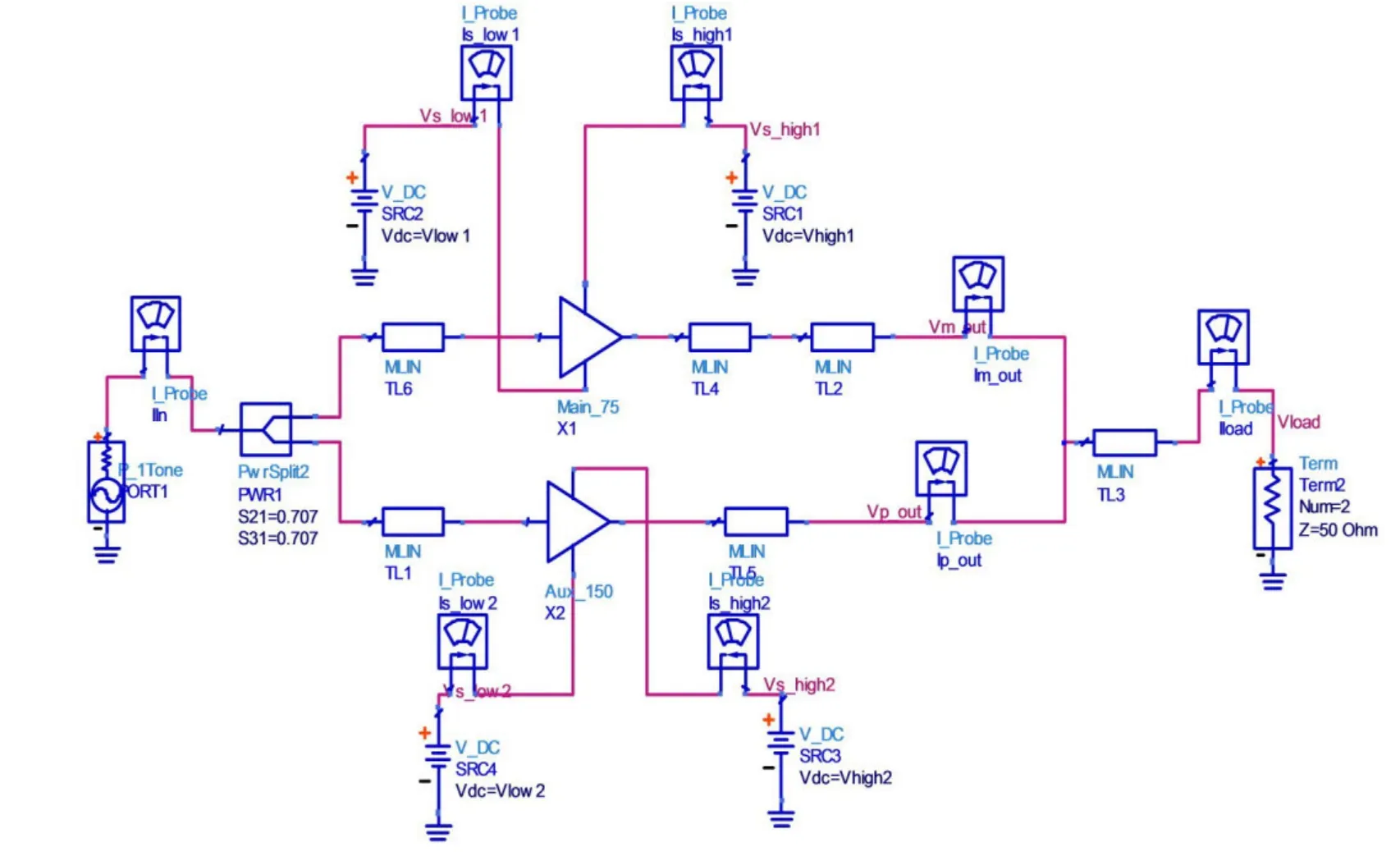
图1 Doherty功放电路原理图

4 模型实验测试

本研究采用的被测设备是一个高功率强非线性非对称DPA，适用于工作在LTE频段的信号激励条件下。对图1中的DPA功放模型进行相关参数的设置，通过仿真提取输入和输出的信号数据。该实验采用了9 000个信号数据点用于建模仿真。建模过程在matlab环境下实现，选取其中的4 000组信号数据，接着，根据公式（6）求解出模型参数并建立有理函数功放模型，将其余的5 000组信号数据用于模型的验证过程。

当记忆多项式模型中M=3，P=5时，模型的系数数目为24((M+1)⋅(P+1))。

当有理函数模型中MN=MD=2，PN=PD=3时，模型的系数数目亦为24((MN+1)⋅(PN+1)+(MD+1)⋅(PD+1))。

利用RMSE和NMSE对模型的时域性能进行评估。NMSE可以表示为：

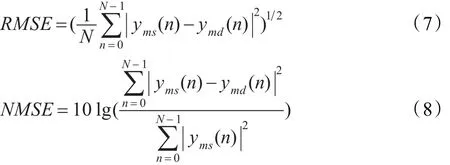
通过仿真得到，模型参数数目同为24的条件下，有理函数模型的RMSE和NMSE与记忆多项式模型的比较如表1所示。

由表1可见，在两模型参数数目相同的前提下，使用有理函数模型进行功放建模，能够获得更好的RMSE和NMSE性能：有理函数模型的RMSE值比记忆多项式模型的RMSE值更趋近于0，并且其NMSE值相比于记忆多项式模型近似提高了24 dB，说明有理函数模型相比于传统的记忆多项式模型降低了模拟功放实际电路的误差。

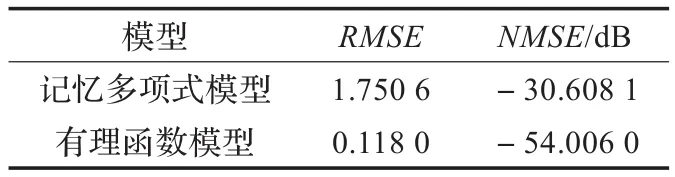
表1 有理函数模型与记忆多项式模型误差比较

图2和图3分别为功放实际输出信号幅度与记忆多项式模型、有理函数模型计算输出信号幅度的比较。由图可见，有理函数模型与记忆多项式模型相比，能够更好地模拟功放实际输出信号的特性，改善误差，提高模拟仿真精度。

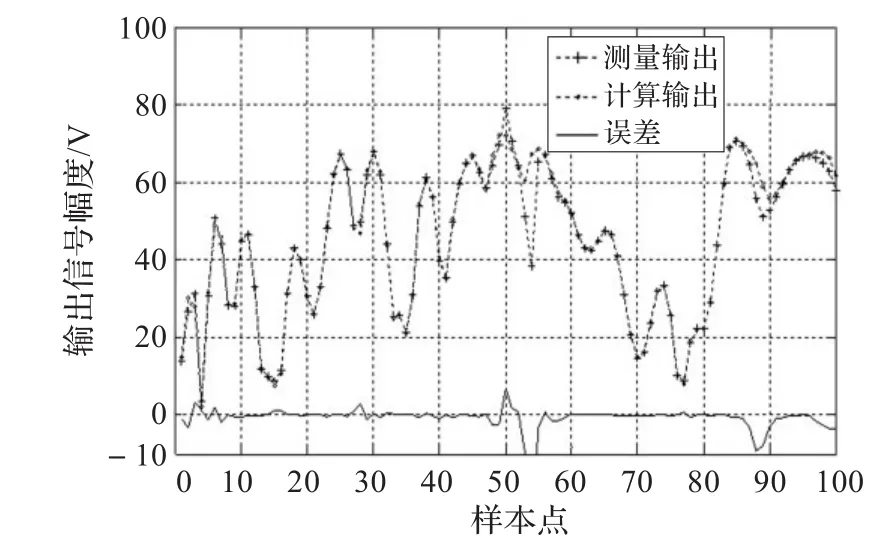
图2 功放与记忆多项式模型输出信号幅度比较

图4（a）为功率放大器与所提及模型的输出功率谱图，图4（b）为将图4（a）局部放大后得到的频谱图。仿真结果可以说明，有理函数模型估计输出的功率谱与功率放大器实际功率谱更加接近，模型体现出更好的性能。

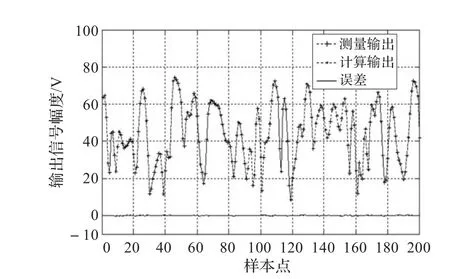
图3 功放与有理函数模型输出信号幅度比较

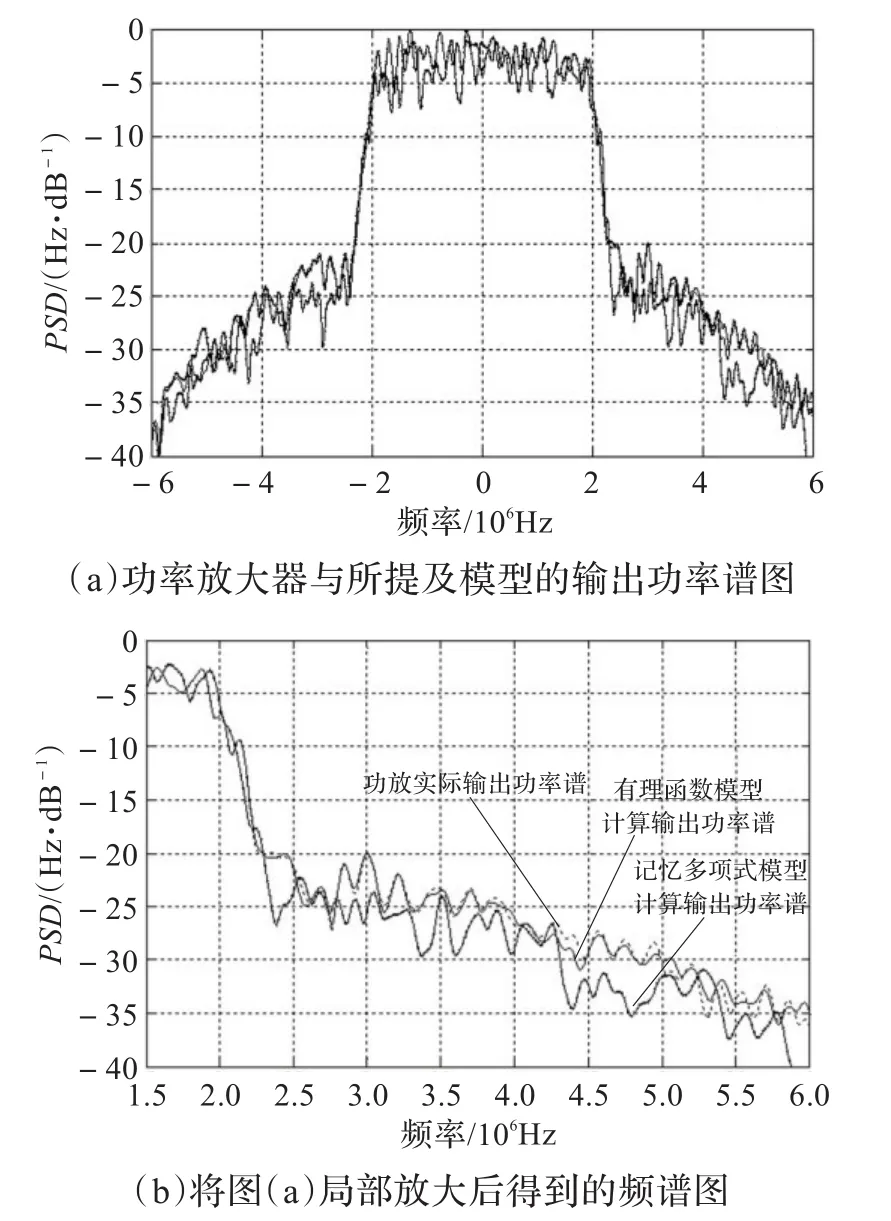
图4 输出频谱图的比较

图5和图6分别给出有理函数功率放大器模型的幅度-幅度调制和幅度-相位调制特性，由图可见，有理函数功放模型输出的预测值和实际功放的测量值十分拟合，甚至在输入大信号幅度驱动功放时，也可确保预测值同测量值之间的较好吻合。另外如图5，可以看出功放的测试和预测幅度-幅度调制曲线呈现出发散状态，而不再为清晰的单一线条，这证明了记忆效应的存在，同时说明了有理函数功放模型能够很好地模拟功放的静态非线性和动态记忆效应。

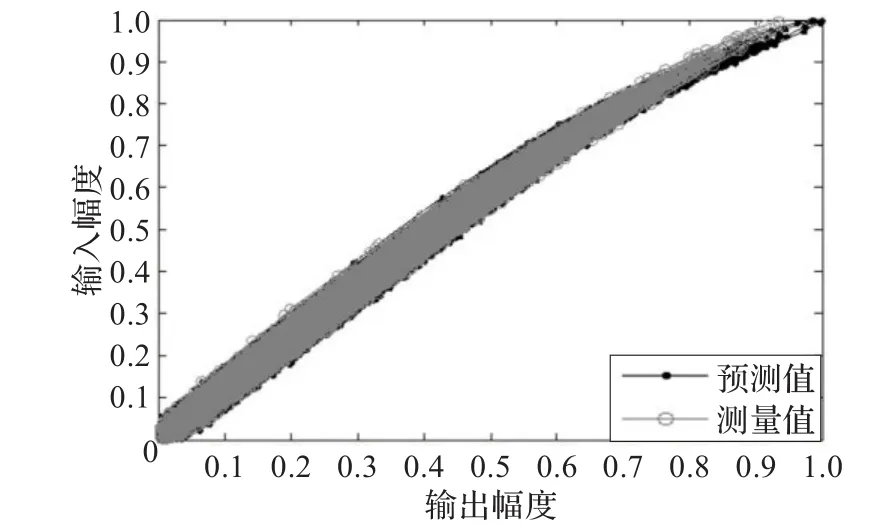
图5 幅度-幅度调制

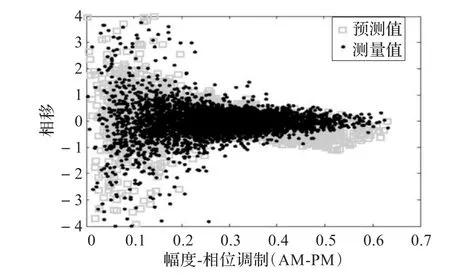
图6 幅度-相位调制

5 结束语

功率放大器的行为级建模可用来模拟实际功放特性，在通信系统的仿真研究中起着重要作用。本文在研究传统记忆多项式模型基础上，提出了面向TD-LTE通信系统的有理函数功放模型，此模型可使用LS技术提取参数，过程简单，不仅可以模拟功放的小信号行为，并且同样能够模拟大信号驱动下的功放特性。对新模型进行仿真实验测试，结果显示，有理函数模型性能更优，相同参数数目条件下，相比于记忆多项式模型NMSE可近似改善24 dB，能够更准确描述射频功放的静态非线性和动态记忆效应。新模型可很好地应用到射频功放线性化预失真系统中，以实现高效利用频谱资源，提高通信质量等目的。

[1]向永波，王光明.线性Doherty功放的优化设计[J].微波学报，2010，26（1）：72-75.

[2]Kim H，Seo C.Improvement of PAE in Doherty amplifier using dual bias control and PBG structure[C]//APMC，2007：1-4.

[3]Kim J，Cha J，Kim I，et al.Optimum operation of asymmetricalcells-based linear Doherty power amplifiers-uneven power drive and power matching[J].IEEE Trans on Microw Theory Tech，2005，53（3）：1802-1809.

[4]郭栋梁，薛红喜.非对称Doherty功率放大器的研究与设计[J].电路与系统学报，2011，16（3）：104-107.

[5]Zhu A，Pedro J C，Brazil T J.Dynamic deviation reduction based Volterra behavioral modeling of RF power amplifiers[J].IEEE Transactions on Microwave Theory and Techniques，2006，54（12）：4323-4332.

[6]TsimbinosJ，LeverK V.Computationalcomplexityof Volterra based nonlinear compensators[J].Electronic Letters，1996，32（9）：852-854.

[7]Li Zhengdai，Yang Dewei，Kuang Jingming，et al.A new joint memory polynomial and look-up-table predistorter algorithm design[C]//Wireless Communications，Networking and Mobile Computing（WiCOM），2011：1-4.

[8]Isaksson M.A comparative analysis of behavioral models for RF power amplifiers[J].IEEE Trans on Microw Theory Tech，2006，54（1）：348-359.

[9]Nan Jingchang，Li Jiuchao.Analysis and simulation of memory effects on microwave power amplifier[C]//Proceedings of the 2009 International Workshop on Information Security and Application （IWISA 2009），2009：205-208.

[10]Saleh A.Frequency-independent and frequency-dependent nonlinear models of TWT amplifiers[J].IEEE Trans on Commun，1981，29（11）：1715-1720.

[11]O’Droma M，Meza S，Lei Y.New modified Saleh models for memoryless nonlinear power amplifier behavioural modelling[J].IEEE Commun Lett，2009，13（6）：399-401.

[12]Li P H，Wang P.Wiener-Saleh modeling of nonlinear RF power amplifiers considering memory effects[C]//Int Conf on Microw and Millimeter Wave Tech（ICMMT-2010），2010：1447-1449.

[13]于翠萍.宽带功率放大器预失真技术的研究[D].北京：北京邮电大学，2009：41-43.

[14]Morgan D R，Ma Z，Kim J，et al.A generalized memory polynomial model for digital predistortion of RF power amplifiers[J].IEEE Trans on Sig Proc，2006，54（10）：3852-3860.

[15]艾渤，李波，钟章队，等.宽带功率放大器预失真原理[M].北京：科学出版社，2011：61-63.

[16]Ding L，Ma Z X，Morgan D R.A least-squares/newton method for digital predistortion of wideband signals[J].IEEE Transactions on Communications，2006，54（5）：833-840.