非均匀杂波中的直接变换域STAP算法研究

程向娇

温州职业技术学院 电气电子工程系，浙江 温州 325000

1 引言

机载预警（AEW）雷达相比于传统地基雷达，由于载机平台处于高空，能够有效解决地物遮挡问题，可以探测低空飞行或者近地目标。然而，当AEW雷达下视工作时，会接收到极强的地杂波，同时由于载机平台处于运动状态，使得地面回波信号具有多普勒扩展性，使得弱目标或者低速目标淹没在杂波中而无法被有效检测。空时自适应处理（Space Time Adaptive Processing，STAP）通过联合空时二维处理，能够有效抑制地杂波，对于提高机载雷达最小可检测速度性能具有重要意义，国内外学者对空时自适应处理展开了广泛研究。

空时自适应处理是空域滤波在空时二维空间中的拓展，由Brennan和Reed于1973年首次提出[1]。由于全空时处理需要进行高维矩阵求逆运算，同时对用于估计杂波协方差矩阵的样本数要求也极为苛刻，根据RMB准则[2]，为使STAP输出SCNR损失小于3 dB，若令N为杂波协方差矩阵维数，至少需要2N-3个距离样本估计协方差矩阵，这两点原因导致全空时自适应处理在实际应用中难以适用。进入20世纪90年代后，硬件计算速度不断升级使得STAP有望在装备中应用，学者们主要从降维和降秩两个方面提出了新算法。降维STAP算法首先进行降维变换，然后在一个局域内进行自适应处理，如辅助通道法（ACP）[3]、因子化算法（FA）、扩展因子化算法（EFA）[4]、局域化联合处理方法（JDL）[5]、空时多波束法（STMB）[6]等。降秩算法则主要有主分量法（PC）[7]、特征相消法（EC）[8]以及互谱法（CSM）[9]。

然而，无论是降维STAP算法还是降秩STAP算法，均需要对杂波协方差矩阵进行估计，而在非均匀杂波中，由于杂波的距离依赖性，使得无法获得足够多的有效样本，这就会导致算法性能急剧下降。有学者提出了直接数据域STAP方法[10]和鲁棒的直接数据域STAP算法[11-13]，在一定程度上可以改善算法的性能，但是依然对目标参数信息具有较大的依赖性，而且，由于在时域中进行截断，具有较大的随意性，回波中的有效信息会被丢掉，使得性能不太理想。另外，文献[14-15]研究了非均匀杂波环境中的目标检测算法。为了使得空时自适应算法能够适用于实际环境，文献[16-18]利用先验信息进行自适应处理，这也是空时自适应处理理论发展的一个重要方向。本文借鉴直接数据域STAP思想，提出一种新的直接变换域STAP算法，首先将空-时二维数据变换到角度-多普勒域中，然后通过选取变换域中某个局域中的通道进行自适应处理。相比于直接数据域中的截断，由于变换域中相邻通道数据相关性更强，因此能够尽可能避免有效信息损失，所以可获得更好的性能。同时，该方法不需要估计杂波协方差矩阵，所以对于非均匀杂波环境中机载雷达的目标检测具有实用价值。

2 机载相控阵雷达信号模型及降维STAP算法

2.1 机载相控阵雷达信号模型

机载相控阵雷达空间坐标模型如图1所示。

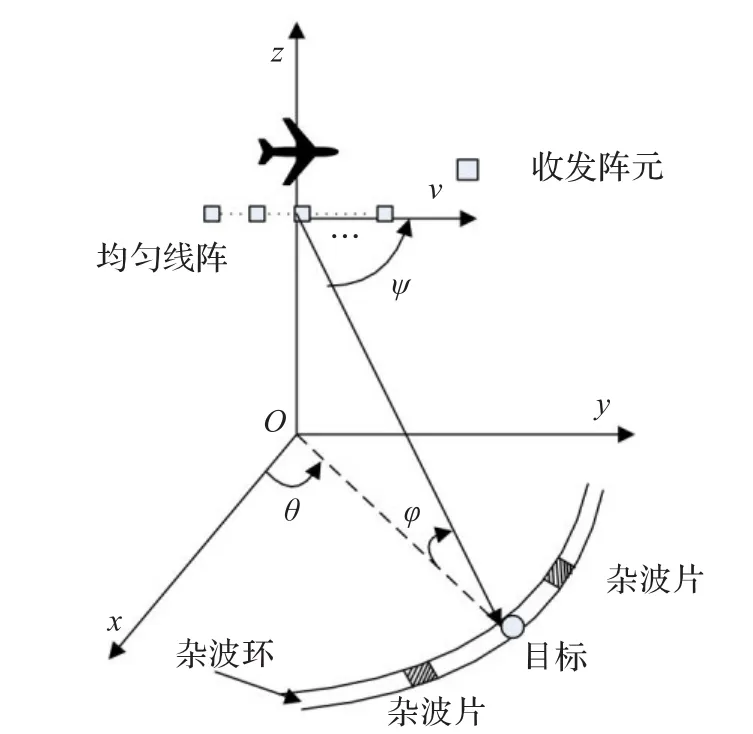
图1 机载相控阵雷达空间坐标模型

在图1中，雷达工作于正侧视模式，以速度v沿y轴水平飞行，发射与接收共阵列，且为线阵，包含N个阵元，阵元间距为半波长λ/2，其中λ为波长，方位角为θ、俯仰角为φ，锥角为ψ，在一个相干处理周期内发射M个脉冲。雷达在运动中，收到地面杂波数据为xc，如有目标时令其回波为s，同时收到热噪声n，其中杂波回波xc为一个距离环上所有杂波片回波积分。令ap表示来自角度ψp的第pth个杂波片的N维空域导向矢量，可表示为：

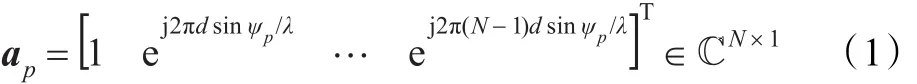
由于载机平台运动，使得每一个杂波片对于载机速度均不同。2vsinψp即为单位时间内载机与角度ψp处的杂波片的相对位移，2vsinψp/λ则为多普勒频率，与脉冲重复频率fr进行归一化，则得到第pth个杂波片归一化多普勒频移fd，p，表示为：

其中，v为载机飞行速度，λ表示波长，Tr表示脉冲重复周期，且Tr=1/fr。第mth个脉冲，杂波片相位延迟为ej2π(m-1)fd，p， 所 以 整个 阵列 在 相干 处理 周 期内 收到 的 第pth个杂波片的信号，如表示为一个N×M矩阵，为：

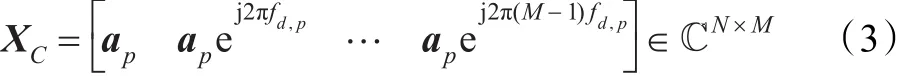
通常，将XC矩阵进行列向量化，即可表示成多普勒导向矢量和空域导向矢量的Kronecker积，即

其中，bp为M维的多普勒导向矢量，为：

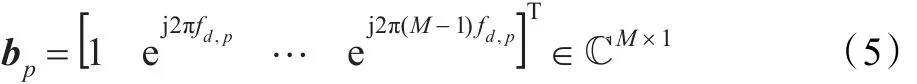
而该距离环上的整个空-时杂波回波xc即为每个杂波片回波的积分，可表示为：

其中，为一个随机的幅度反射变量，NC为整个杂波环所划分的杂波片的个数。

对于降维或者降秩STAP算法，需要估计杂波协方差矩阵，用R∈ℂNM×NM表示为：

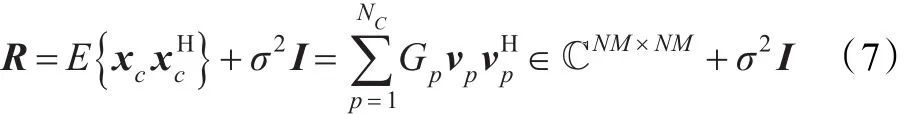
其中，Gp为一常数，与该方向的发射增益成正比。通常，认为阵列噪声为高斯白噪声，为了推导方便，令噪声功率为0 dB，即σ2=1。

2.2 机载相控阵雷达信号模型

空时自适应处理的目的就是要设计一组权值，对N个阵元M个脉冲的输出进行加权求和，如图2所示。其中xn，m表示第n个阵元第m个脉冲匹配滤波输出。最优权值w的选取准则为：

其中，R为回波不包含目标时的杂波协方差矩阵，即在保证系统对给定方向特定多普勒频率的目标信号增益不变的情况下，使系统输出的功率最小，其最优解为：

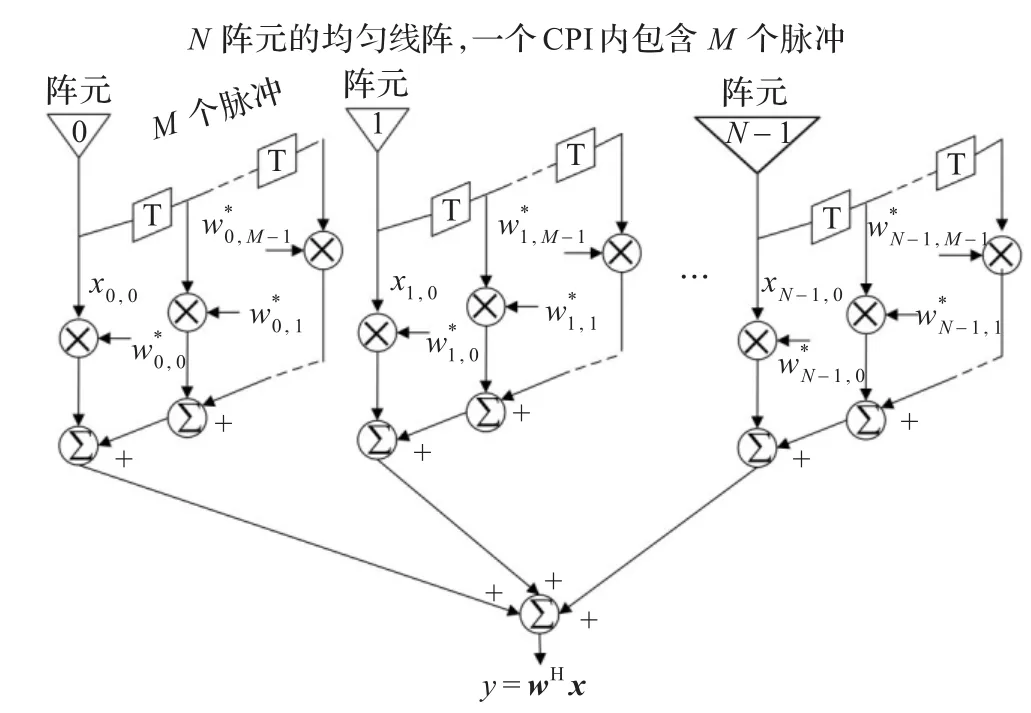
图2 空时处理结构示意图

其中，系数μ=1/(sHR-1s)，此时最大输出SCNR为：

降维STAP首先将回波数据从空-时域中变换到角度-多普勒域，可以通过二维DFT直接实现此种变换，如图3所示。

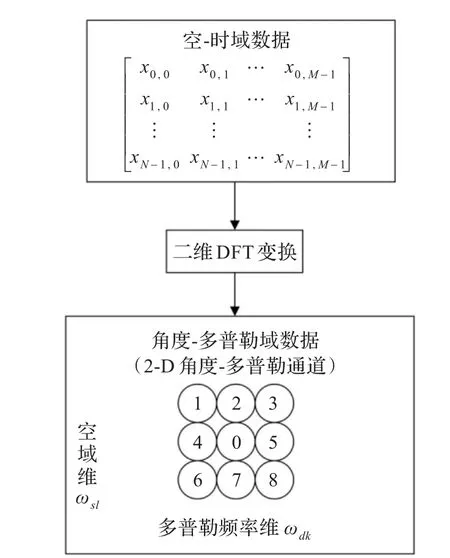
图3 空时处理结构示意图

令xT为时域数据x变换到角度-多普勒域中对应的列矢量，sT表示时域期望信号s变换到角度-多普勒域中对应量。在形成的角度-多普勒平面内，每个空时二维波束可以表示为：

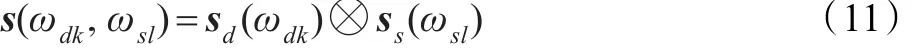
其中，ωsl(l=1，2，…，N)和ωdk(k=1，2，…，M)表示空间频率和多普勒频率，sd(ωdk)是一个对应于期望频率为ωdk的M维的时域导向矢量，ss(ωsl)为一个对应于空域频率为ωsl的N维的空域导向矢量，则sH(ωdk，ωsl)x即可表示x在角度-多普勒平面中对应通道(ωdk，ωsl)的输出。

通过组合不同的l和k，即可得到所有的角度-多普勒频率的二维通道数据，而降维处理则只需要得到其中一部分通道，此时的降维矩阵用T表示。变换域中的杂波协方差矩阵为RT，可表示为：

其中xT=THx，T为从空-时域变换到角度-多普勒域的降维变换矩阵。根据维纳滤波理论，变换域中最优权向量wT应等于：

将数据从空-时域变换到角度-多普勒域中，能够起到一种凝聚的作用，相邻通道中杂波分量具有高度相关性，更有利于自适应处理和杂波对消。变换域中的杂波协方差矩阵RT需要通过其他距离环数据进行估计，最终输出信杂噪比可计算为：

3 直接变换域STAP算法

对于不同的波束域降维算法，它们选择不同的角度-多普勒通道作为辅助通道用于杂波对消，若用T1表示不降维从空时数据域变换到角度多普勒域的变换矩阵，用T表示降维变换矩阵，则不同降维方法也就在于从T1中抽取得到T的方法不同，如图4所示。

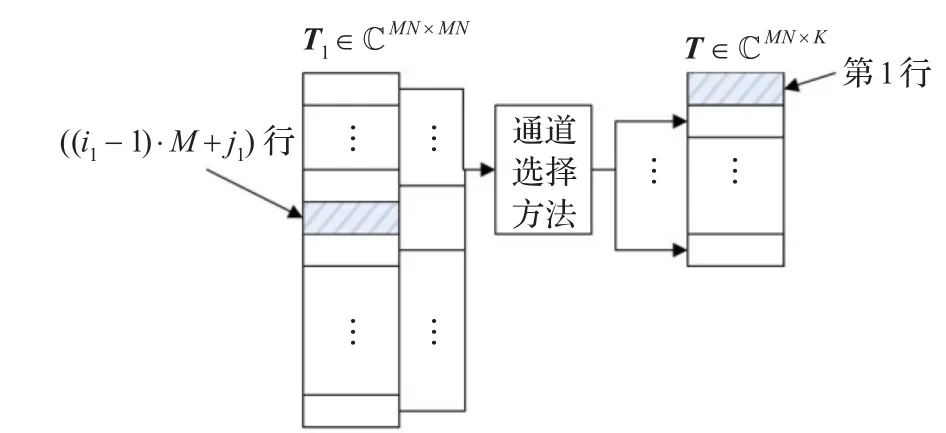
图4 不同波束域降维算法辅助通道选择方法

在JDL降维STAP处理中，在角度-多普勒域中主通道周围选择相邻通道作为辅助通道进行杂波对消，其权值计算如式（13）所示。

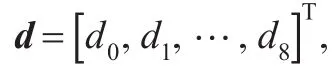
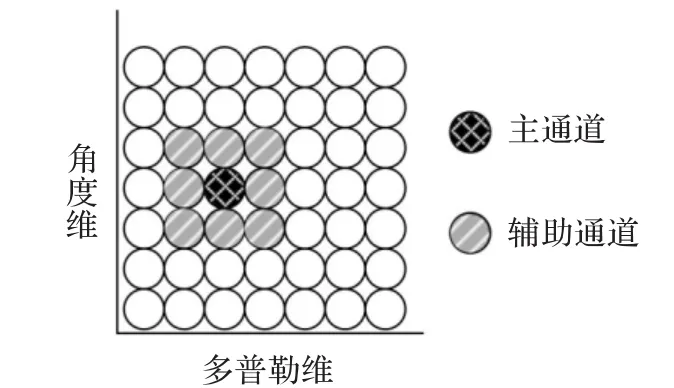
图5 JDL降维STAP算法辅助通道选择方法

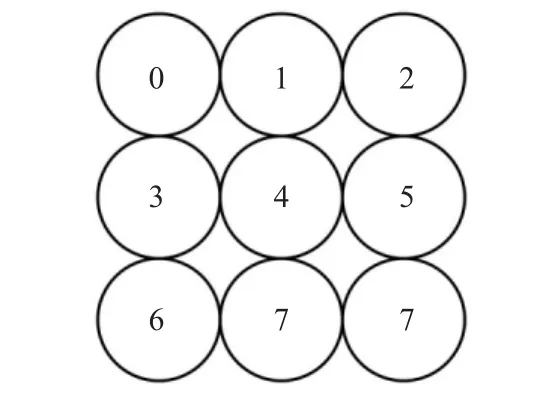
图6 通道编号方法示意

如果选择更多的通道数，其选择依据与JDL类似，选择主通道相邻近的通道，称之为通道的截断。各个通道的区别在于对准不同的角度频率或者多普勒频率，且决定于阵元个数和脉冲个数，如果将通道之间进行角度频率或者多普勒频率补偿然后进行相减，令zd=ej2π/M，zs=ej2π/N，则可构成一系列的关系式。

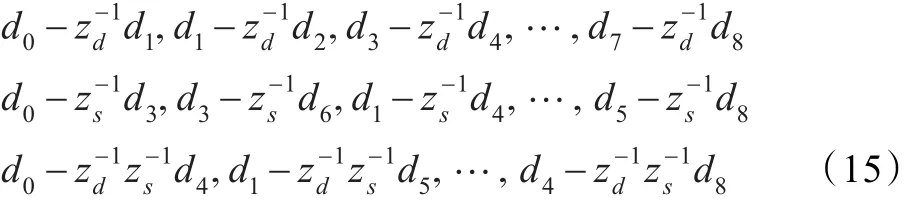
可以利用这些独立的不同关系式来达到抑制杂波的效果，将以上关系式按照行来构造一个矩阵D2，此时设计的一组权值记为w，则不通过估计杂波协方差矩阵，权值求取的准则应为：

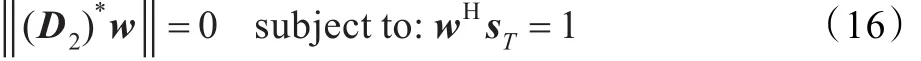
在式（16）中，‖⋅‖表示2-范数，其意义是将输出最小化，而非将输出抑制为0，得到式（16）后则可通过最小均方的方式对上式求解，得到最优加权矢量w。

4 仿真

阵列包含阵元个数N为16，波长λ为0.03 m，阵元间距为λ/2，目标方向位于正侧视零度方向，发射相干脉冲个数为16个，载机飞行速度v为200 m/s，以输出信杂噪比损失为指标对比直接变换域与直接时域STAP算法性能，输出信杂噪比损失定义为当前输出信杂噪比与最优信杂噪比之差，而最优信杂噪比即为杂波完全抑制时的输出，如图7所示。

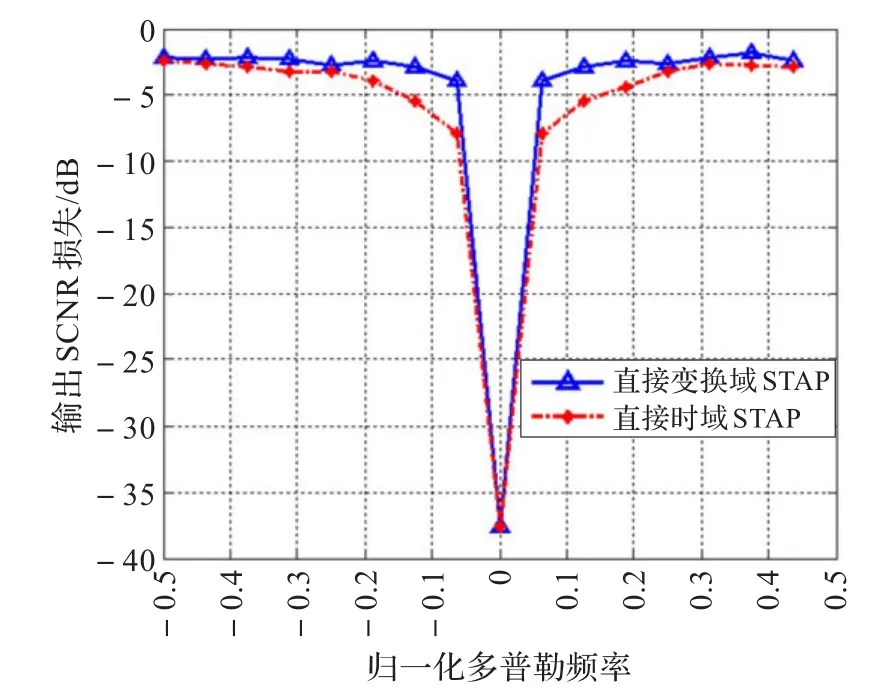
图7 直接变换域与直接时域算法性能对比

如图7所示，直接变换域算法具有优势，尤其是在主瓣杂波区，直接变换域具有明显优势，具体地，如当归一化多普勒频率小于0.2时，直接变换域算法输出信杂噪比相对于直接数据域算法大约有3 dB的提升，这相当于探测相同速度目标的探测距离可以增加一倍，更有利于探测低速弱目标。

为了测试算法稳健性，当目标速度与通道速度具有一定偏差时，由于仿真条件中设置阵元个数为16，则空域划分了16个通道，性能最为恶化处应为各个通道相交处，即归一化角度偏差在通道对准基础上摆动±1/32，当角度偏差在[-1/32，1/32]变化时，仿真结果如图8所示。

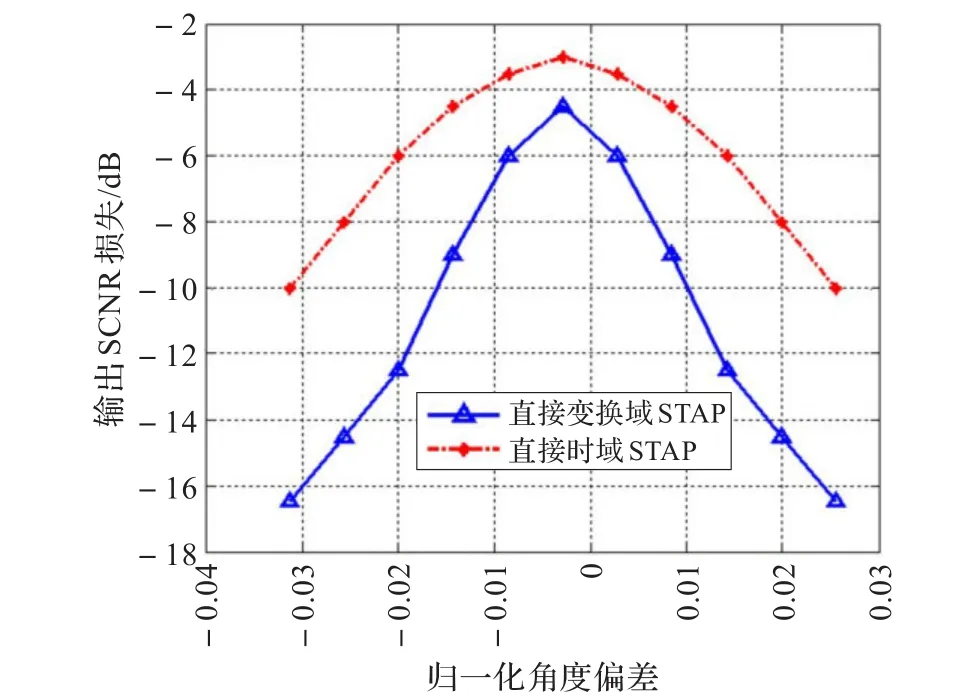
图8 目标角度频率与空域通道偏差输出SCNR损失

从图8可以看出，本文提出算法对于角度偏差具有较好的鲁棒性，相比于直接时域STAP算法，能够提升2～6 dB。

5 结束语

本文提出一种直接变换域STAP算法，不需要通过其他距离环样本对当前杂波统计特性进行估计，适用于具有非均匀杂波中的机载雷达目标检测。相比于直接数据域STAP，通过变换使得杂波能量更集中，通道之间相关性更强，对于数据截断可以损失更少的信息，故所提出的算法性能优于直接数据域STAP，仿真结果验证了这一点。

[1]Reed I S，Mallett J D，Brennan L E.Rapid convergence ratein adaptivearrays[J].IEEE Transactionson Aerospace and Electronic Systems，1974，10（6）：853-863.

[2]Klemm R.Principles of space-time adaptive processing[M].[S.l.]：IET，2002.

[3]Dipieto R C.Extended factored space-time processing technique for airborne radar[C]//25th Asilomar Conference，Pacific Grove，CA，1992：425-430.

[4]Wang H，Cai L.On adaptive spatial-temporal processing for airborne surveillance radar systems[J].IEEE Transactions on Aerospace and Electronic Systems，1994，30（3）：660-669.

[5]Wang Y L，Peng Y N.Space-time joint processing method for simultaneous clutter and jamming rejection in airborne radar[J].Electronic Letters，1996，32（3）：258-259.

[6]Abramovich Y I，Rangaswamy M，Johnson B A，et al.Performance analysis of two-dimensional parametric STAP for airborne radar using KASSPER data[J].IEEE Transactions on Aerospace and Electronic Systems，2011，47（1）：118-139.

[7]Haimovich A M.An eigencanceler：adaptive radar by eigenanalysis methods[J].IEEE Transactions on Aerospace and Electronic Systems，1996，32（2）：532-542.

[8]Goldstein J S，Reed I S.Reduced rank adaptive filtering[J].IEEE Transactions on Signal Processing，1997，45（2）：492-496.

[9]Sarkar T K，Wang H，Park S，et al.A deterministic leastsquares approach to Space-TimeAdaptive Processing（STAP）[J].IEEE Transactions on Antennas Propagation，2001，49（1）：91-103.

[10]Cristallini D，Burger W.A robust direct data domain approach for STAP[J].IEEE Transactions on Signal Processing，2012，60（3）：1283-1294.

[11]Yang E，Adve R，Chun J.Hybrid direct data domain sigmadelta space-time adaptive processing algorithm in nonhomogeneous clutter[J].Radar，Sonar&Navigation，IET，2010，4（4）：611-625.

[12]Cristallini D，Bürger W.A robust direct data domain approach for STAP[J].IEEE Transactions on Signal Processing，2012，60（3）：1283-1294.

[13]Xing Gaoxiang，Cai Zhiming.A sidelobe-constraint direct data domain leastsquare algorithm[C]//Proc 2nd Int Congress on Image and Signal Process（CISP 2009），2009：1-4.

[14]Wang Pu，Li Hongbin，Himed B.A parametric moving target detector for distributed MIMO radar in nonhomogeneous environment[J].IEEE Transactions on Signal Processing，2013，61（9）：2282-2294.

[15]Yang Xiaopeng，Liu Yongxu，Long Teng.Robust nonhomogeneity detection algorithm based on prolate spheroidal wave functions for space-time adaptive processing[J].Radar，Sonar&Navigation，IET，2013，7（1）：47-54.

[16]Tang B，Tang J，Peng Y.Performance of knowledge aided space time adaptive processing[J].IET Radar Sonar&Navigation，2011，5（3）：331-340.

[17]Zhu X，Li J，Stoica P.Knowledge-aided space-time adaptive processing[J].IEEE Transactions on Aerospace and Electronic Systems，2011，47（2）：1325-1336.

[18]Stoica P，Li J，Zhu X，et al.On using a priori knowledge in space-time adaptive processing[J].IEEE Transactions on Signal Processing，2008，56（6）：2598-2602.