小波分析在脉冲涡流无损探伤中的应用

段晓帅，陈世利，靳世久

天津大学 精密测试技术与仪器国家重点实验室，天津 300072

1 引言

脉冲涡流无损探伤是铝合金板材的重要探伤手段之一。它具有以下优点：可穿透铝合金板材表面非金属覆盖物、无需耦合剂以及一次扫描就可以检测不同深度缺陷等[1-2]。脉冲涡流的激励信号为方波信号，检测信号的实质就是系统对阶跃信号的瞬态响应。

在铝合金板材探伤中，检测信号是由大量瞬态信号组成的一次扫描波形。一般通过“微观”地分析峰值最大的那次瞬态信号，由其峰值大小和过零时间定量检测缺陷深度；通过“宏观”地分析整个一次扫描波形，提取波形的峰值扫描曲线，由两个极值点的时间间隔定量检测缺陷长度[3-4]。但通常存在以下两个问题：（1）瞬态信号中存在高频噪声，过零时间难以确定。对于该问题，传统方法采用低通滤波器滤除高频噪声[5-6]，但该方法在滤除高频噪声的同时损害了真实信号特征，削减了真实信号的峰值，造成真实信号相位延迟，改变了真实过零时间。（2）由于铝合金板材表面粗糙度等原因，由一次扫描波形直接提取的峰值扫描曲线存在抖动，两个极值点的时间难以确定。

小波变换采用时域和频域的局部变换，能有效提取出信号在不同尺度下的信息，被誉为“数字显微镜”。本文基于小波的以上特点，将信号进行多尺度分解，得到信号在多个时间-尺度平面上的信息。对分解后的高频尺度信号进行阈值去噪，在保留瞬态信号特征的基础上，消去了高频噪声，还原了真实信号的峰值和过零时间。如果只对大尺度下的小波近似系数进行重构，再提取重构信号的峰值扫描曲线，则可以消除抖动，提高极值点的时间定位准确度。

2 脉冲涡流探伤原理及信号特点

2.1 脉冲涡流对缺陷定量检测的原理

在激励方波的上升沿，激励线圈激发的强大磁场使被测铝合金板中产生涡流信号，涡流信号产生持续衰减的磁场，检测线圈获取这个变化的磁场后将感应出随时间变化的瞬态电压信号[7-8]，此感应电压信号具有先急速增大后缓慢衰减的突变特点，为非线性非平稳信号。

理想的脉冲涡流瞬态信号如图1所示。图中的峰值表示瞬态信号的最大值，过零时间表示激励方波上升沿到瞬态信号零点的时间间隔。峰值和过零时间随缺陷的深度变化而变化，而与缺陷的长度无关。

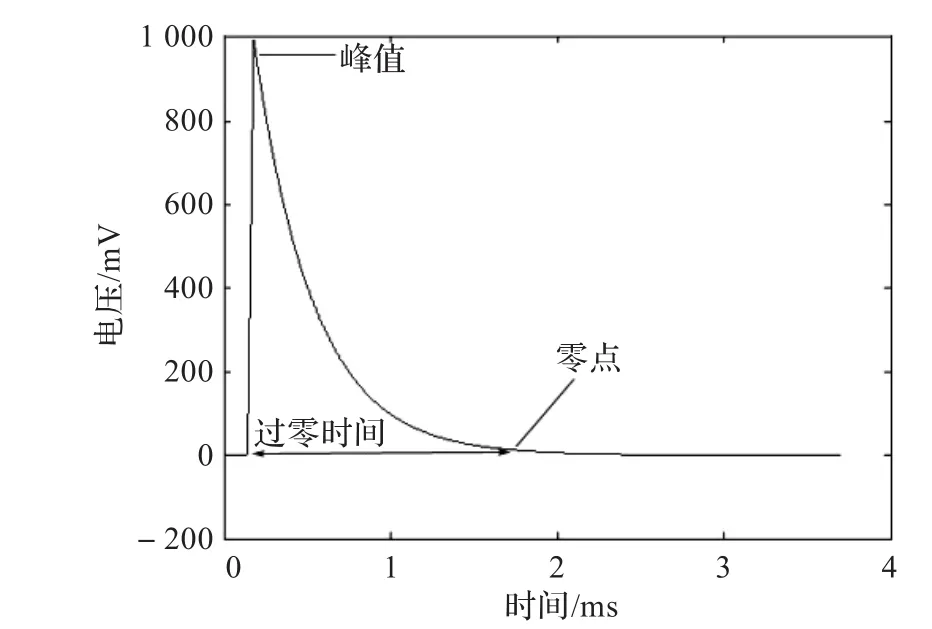
图1 理想的脉冲涡流瞬态信号

在实际检测时，大量瞬态信号组成探头的一次扫描波形，提取峰值扫描曲线后，其两个极值点的时间间隔与缺陷长度成正比关系。理想的峰值扫描波形如图2所示，缺陷长度的计算公式为：

式中L表示缺陷长度，v表示探头扫描速度，Δt表示两个极值点时间间隔，t1和t2表示两个极值点时间。

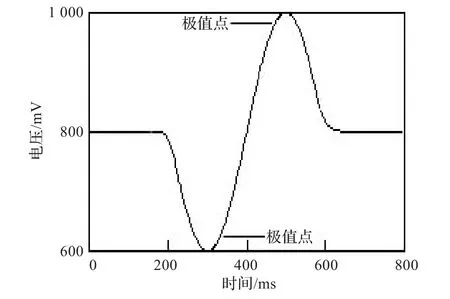
图2 理想的峰值扫描波形

2.2 脉冲涡流实际检测信号的特点

实际检测时，脉冲涡流信号难免会混入噪声，对信号造成污染，含有噪声的瞬态信号通常如图3所示。由于噪声的干扰，信号零值点附近存在波动，给过零时间判断带来困难，而且峰值中含有噪声成分，直接影响缺陷深度的检测准确度。

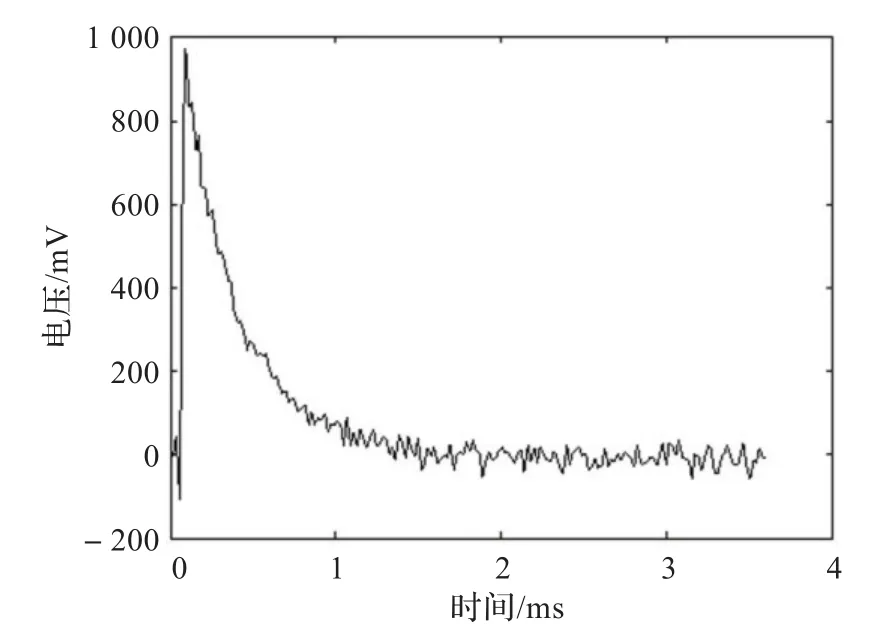
图3 含有噪声的瞬态信号

另外，由于铝合金板材表面粗糙度和表面微小堆积物的影响，峰值扫描曲线难免会存在抖动。实验得到的峰值扫描曲线如图4所示，由于抖动的存在，峰值扫描曲线两个极值点时间难以判断，直接影响缺陷长度的检测准确度。

3 小波多分尺度分析和阈值去噪

3.1 小波多尺度分析思想

在使用小波对信号分析时，通过对小波基的缩放来实现尺度的变化。缩放因子越大，尺度越大，度量的是信号的近似部分，近似部分在频谱中一般表现为低频。缩放因子越小，尺度越小，度量的是信号的细节部分，细节部分在频谱中一般表现为高频部分[9]。实际工程应用中，信号的近似部分一般代表着信号的“走势”，而细节部分起着对信号进行修饰的作用。

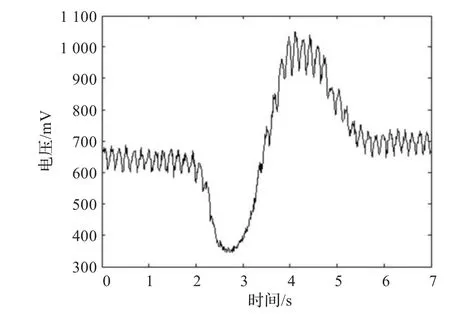
图4 实验得到的峰值扫描曲线

基于上述理论及思想，可以把峰值扫描曲线的走势看作信号的近似部分，把抖动看作信号的细节部分。为了消除细节上的抖动，对信号做小波分解后，只利用近似系数进行重构，再提取重构信号的峰值扫描曲线，达到消除抖动的目的。

3.2 小波的阈值降噪

在用小波对含噪声信号进行多尺度分解时，信号和噪声在小波域中有不同的性态表现，它们的小波系数幅值随尺度变化的趋势不同。随着尺度的增加，噪声系数的幅值衰减很快，而真实信号系数的幅值衰减比较慢，并且有用信号对应的系数幅值较大，而噪声对应的小波系数幅值较小[10]。

小波阈值去噪的步骤包括小波分解、系数阈值处理以及信号重构三个部分[11]。其中最为关键的就是第二步的系数阈值处理，它直接影响信号的去噪效果[12]。常用的小波阈值处理方法分为硬阈值法和软阈值法，处理方法分别如公式（2）和公式（3）所示。

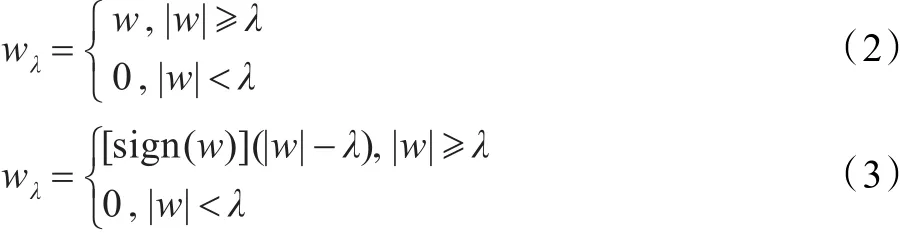
公式（2）和公式（3）中wλ表示处理后的系数，w表示处理前的系数，λ表示临界阈值。

小波阈值去噪的基本思想是，当小波系数小于临界阈值时，认为这部分的信号主要是噪声，应当舍弃，把这部分的小波系数置零；当小波系数大于临界阈值时，认为这部分信号主要是有用信号，那么就把这部分的小波系数保留下来或者按固定量向零收缩，前者是硬阈值处理方法，后者是软阈值的处理方法。

在包含尖峰的突变信号中，有用信号的频谱很宽，与噪声在频谱上产生叠加，且现实中噪声往往持续在整个时域上，这给保留原始信号的同时滤除噪声造成困难。此时对信号做小波分解后，得到的小波系数必然是真实信号和噪声共同作用的结果。由公式（2）可知，当采用硬阈值去噪后，大于临界阈值的小波系数不作处理，没有达到滤除噪声的目的；由公式（3）可知，软阈值法对大于临界阈值的小波系数进行收缩，收缩后的小波系数就是真实信号，而收缩去掉的那部分小波系数就是噪声。可见，软阈值法可以把原始信号的小波系数和噪声的小波系数分离开，在保留原始信号的同时滤除噪声。

脉冲涡流检测的瞬态信号的频谱较宽，且峰值部分包含了高频信号，与噪声在频域上产生叠加。所以对脉冲涡流信号进行小波分解后，幅值在阈值以上的小波系数并不是完全“干净”的，而是真实信号的小波系数与噪声的小波系数叠加的结果，致使实验得到的峰值比真实峰值大，给缺陷深度的检测带来误差。

由于硬阈值法和软阈值法采用不同的阈值函数，则必然会在瞬态信号去噪中产生不同的效果。由公式（2）可知，硬阈值法完全保留大于阈值的小波系数，所以不能去除瞬态信号峰值中的噪声成分。而根据公式（3），软阈值法对于大于阈值的小波系数会进行削减，且削减大小为阈值大小，可以很好地去除瞬态信号峰值中包含的噪声成分，还原真实信号的峰值度。下文将基于实验对此验证。

4 实验与比较

4.1 实验系统的搭建

实验系统框图如图5所示，ARM处理器根据触摸屏的输入参数产生相应脉冲信号。脉冲信号经过固态继电器和稳压源后功率被放大，以使激励线圈能够在试块中产生足够强度的涡流。检测线圈获取涡流产生的磁场后感应出电压信号，电压信号经过调理电路放大后通过NI数据采集卡USB-4431保存在计算机中。数据采集和保存采用LabVIEW完成，后期小波处理采用Matlab完成。

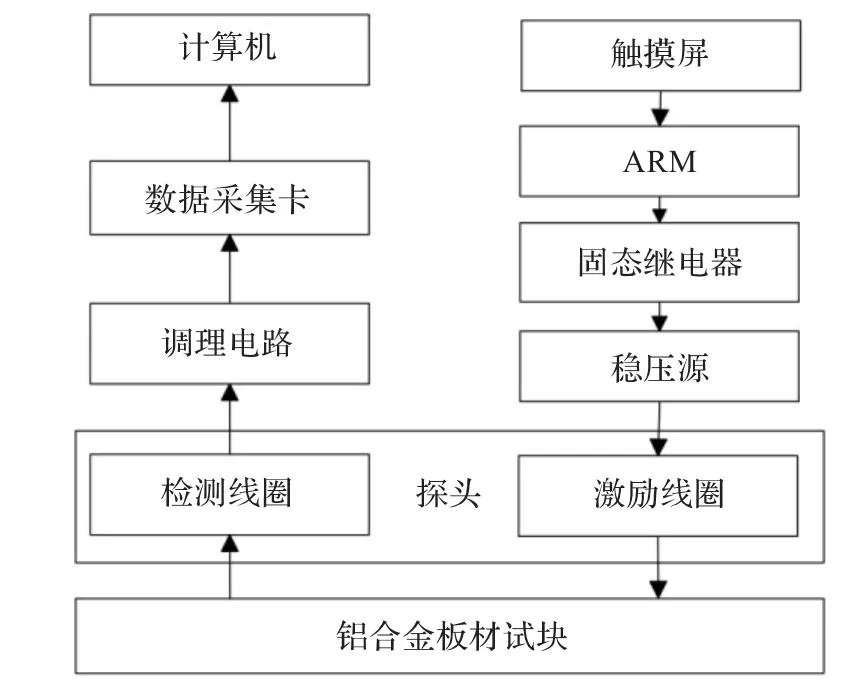
图5 实验系统框图

图6为实验系统照片。实验中激励脉冲频率为100 Hz，稳压源输出电压为10 V。数据采集卡采样率为50 kHz。探头扫描速度为5 mm/s。

图6 实验系统照片

4.2 瞬态信号阈值去噪的实验结果

实验中采用coif4函数作为小波基，对信号做4层分解后，得到4组细节系数，对这4组细节系数分别设置阈值。

为了比较硬阈值法和软阈值法在瞬态信号去噪中的不同效果。本文分别对这两种阈值方法进行了实验，结果显示在图7中。

图7（a）和图7（b）分别表示硬阈值法和软阈值法去噪后信号与原始信号在零点附近的比较。图7（c）和图7（d）分别表示硬阈值法和软阈值法去噪后信号与原始信号在峰值附近的比较。

对比图7（a）和图7（b）可以看出，在零点附近，两种阈值法去噪后的信号噪声都得到了有效抑制，但软阈值法去噪后的信号比硬阈值法去噪后的信号更为光滑，这是因为硬阈值法处理后的小波系数在间断点处产生震荡造成的，而软阈值法不存在这个问题[13]。

对比图7（c）和图7（d）可以看出，硬阈值处理后的信号的峰值与原始信号峰值几乎相等，而软阈值去噪后的信号峰值比原始信号减小一些。由公式（3）可知，减少的这一部分即是预先设定的阈值大小。由此可见，实验结果与上文中的理论分析结果一致。

通过硬阈值法和软阈值法去噪信号比较可知：相对于硬阈值法，软阈值法去噪信号在还原真实峰值大小的基础上，避免了震荡现象，可见软阈值法在脉冲涡流瞬态信号去噪中效果更好。

在传统方法中，一般采用低通滤波器滤除脉冲涡流信号中的高频噪声。本文对低通滤与小波软阈值去噪方法做了比较实验，实验结果如图8所示。由图可见，低通滤波器虽然能够有效去除瞬态信号中的高频噪声，但却付出了严重的代价：由于完全滤除了峰值部分的高频部分，导致真实峰值遭到严重衰减；且相位延迟严重，改变了真实的过零时间，给缺陷深度的定量检测带来误差。而采用小波软阈值去噪可以克服低通滤波器的这些缺点。

4.3 峰值扫描曲线抖动的消除实验结果

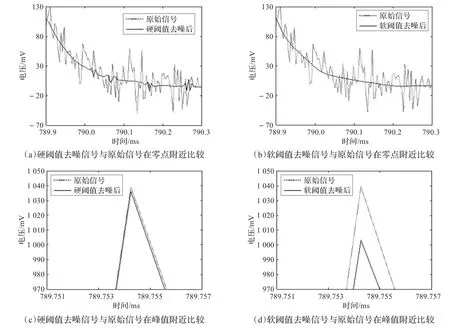
图7 不同阈值方法对瞬态信号去噪效果的比较

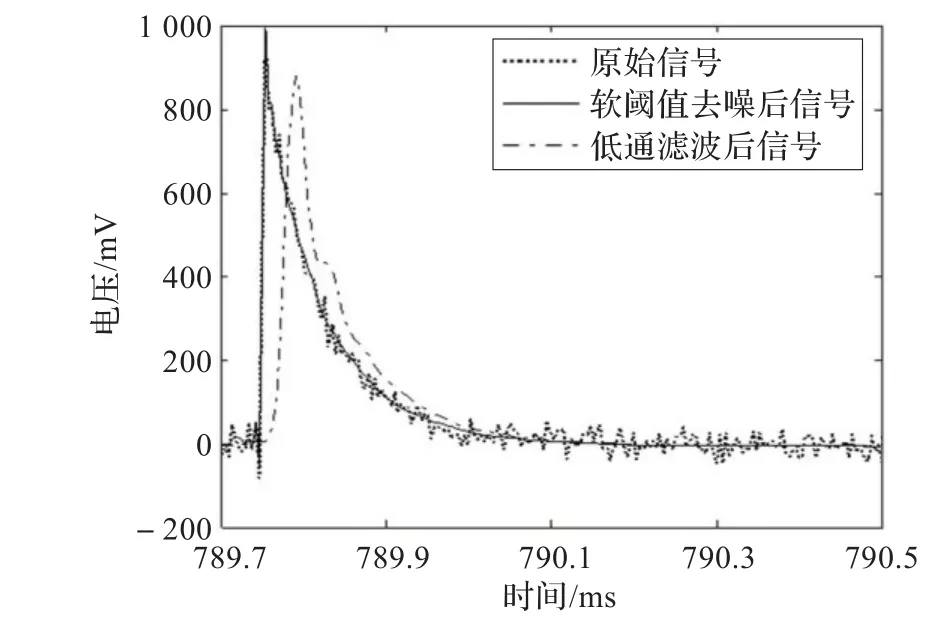
图8 软阈值去噪与低通滤波在瞬态信号中的比较

实验中同样采用coif4函数作为小波分解基，分解层数的选择对实验结果也有重要的影响：分解层数太小，由近似系数重构的信号将包含太多的细节信息，导致峰值扫描曲线消除抖动不彻底；分解层数太大，由近似系数重构的信号将舍弃太多信息，导致峰值扫描曲线失真严重。

如图9所示为采用不同分解层数时，由近似系数重构信号所得峰值扫描曲线。为了便于比较，图中数据已做归一化处理。从图中可以看出，当采用3层分解时，实验效果最好。

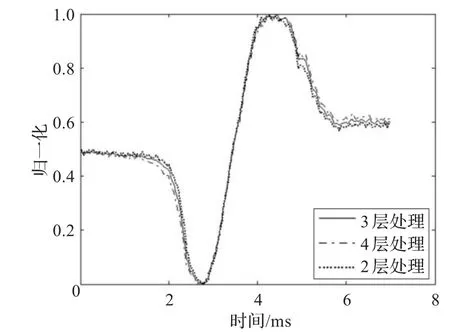
图9 不同分解层数的实验效果对比

图10为采用3层分解后，由近似系数重构信号提取的峰值扫描曲线。对比图10和图4可以发现，对信号进行小波3层分解后，由近似系数重构信号提取的峰值扫描曲线变得光滑，抖动大大减小，两个极值点时间变得更加明确。

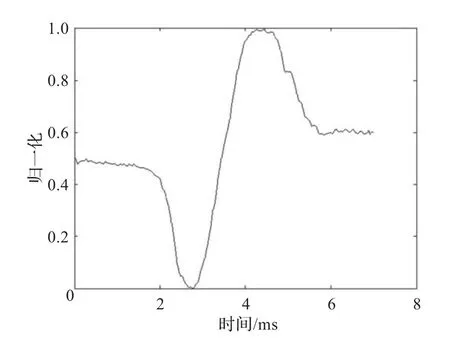
图10 采用3层分解后，得到的峰值扫描波形

4.4 小波处理后，缺陷定量检测的实验结果

实验所用铝合金试块尺寸为270 mm×100 mm×25 mm（长×宽×厚）。在试块上加工了9个凹槽来模拟不同缺陷，见图11。单次实验结果如表1所示，其中计算直径由探头扫描速度乘以极值点时间差计算所得（见公式（1）），实验中的探头扫描速度约为5 mm/s。

图11 不同尺寸参数的凹槽

综合表1实验数据可知，对一次扫描波形做小波分解后，由近似系数重构得到曲线，再提取其峰值扫描曲线，由于该方法可以消除细节抖动，两个极值点时间变得更加明确，直接提高了缺陷长度的检测准确度。

5 结束语

5.1 讨论

（1）对于瞬态信号去噪，另外常用的处理非线性非平稳信号的方法还有EMD分解法[14]。一般使用EMD分解法对非线性非平稳信号去噪时，先把信号分解成若干固有模态函数，再对固有模态函数采取类似于小波阈值处理的方法进行处理，以达到去除噪声的目的。

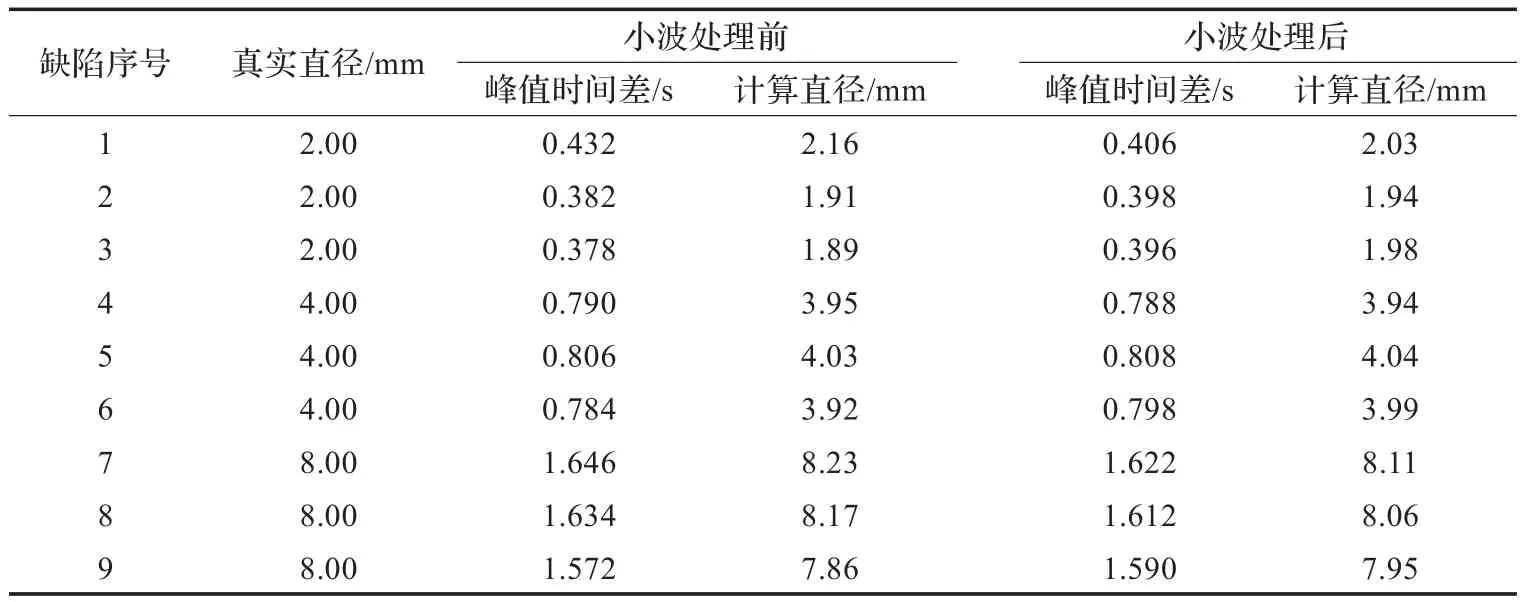
表1 缺陷长度定量检测比较的实验结果

EMD分解法尚处于发展时期，还有很多问题亟待解决，比如边界端点效应以及模态混叠现象，这些问题处理不好，将直接影响EMD的分解结果和去噪效果。Boudraa等人对EMD消噪算法和小波阈值算法进行比较发现，EMD消噪算法整体上不如小波阈值消噪算法[15]。

另外，文献[16]中提到，EMD的分解速度相比于小波分解太慢，不符合脉冲涡流探伤系统实时性的要求。

（2）对于一次扫描波形，常用的提取信号趋势的方法有平均斜率法、差分法、EMD分解法等。但本文中提到的一次扫描波形信号的“走势”不同于传统的信号“趋势”概念。这里提到的“走势”表示一次扫描波形由于缺陷而导致的包络的大起伏，传统的信号“趋势”是指信号中周期大于采样长度的频率成分，所以传统的提取信号趋势的方法在本文中不可行。

5.2 总结

本文主要研究了小波分析在铝合金板材脉冲涡流探伤中的两方面应用。

（1）对于瞬态信号，使用小波阈值去噪对其处理。由于噪声的影响，瞬态信号的零点附近存在抖动，导致过零时间不易判断，且由于瞬态信号峰值中包含高频信号，与噪声在频域上叠加，致使瞬态信号峰值比真实值大。本文对硬阈值法和软阈值法的原理进行分析比较，分析两者在瞬态信号去噪中的影响并进行实验验证。通过实验证明软阈值法可以在还原真实峰值的基础上，避免了震荡现象。可见软阈值法在脉冲涡流瞬态信号去噪中效果更好，且可以解决传统低通滤波带来的峰值衰减、相位延迟等问题。

（2）对于一次扫描波形，把峰值扫描波形的走势看作信号的近似部分，波形的抖动看作信号的细节部分。基于以上思想，本文对一次扫描波形做小波分解，只对近似系数重构。实验证明：与原始信号所提取的峰值扫描曲线相比，经过本文方法得到的峰值扫描曲线变得光滑，极值点的时间判断更加明确，提高了缺陷长度的检测准确度。

[1]Adewale I D，Tian G Y.Decoupling the influence of permeability and conductivity in pulsed eddy-current measurements[J].IEEE Transactions on Magnetics，2013，49（3）：1119-1127.

[2]Zhang Yuhua，Sun Huixian，Luo Feilu，et al.Detection of a defect based on 3D magnetic field measurement for pulsed eddy current testing[J].Chinese Journal of Sensors and Actuators，2008，21（5）：801-805.

[3]Lebrun B，Jayet Y，Baboux J C，et al.Pulsed eddy current signal analysis：application to the experimental detection and characterization of deep flaws in highly conductive materials[J].NDT&E International，1997，30（3）：163-170.

[4]杨宾峰.脉冲涡流无损检测若干关键技术研究[D].长沙：国防科学技术大学，2006.

[5]张世雄，宋文爱，陈以方，等.基于LabVIEW的脉冲涡流检测系统[J].无损检测，2009，31（1）：12-14.

[6]杨宾峰，张辉，赵玉丰，等.基于新型脉冲涡流传感器的裂纹缺陷定量检测技术[J].空军工程大学学报：自然科学版，2011，12（1）：73-77.

[7]Tian G Y，Sophian A.Defect classification using a new feature for pulsed eddy current sensors[J].NDT&E International，2005，38（1）：77-82.

[8]Li Shu，Huang Songling，Zhao Wei.Development of differential probes in pulsed eddy current testing for noise suppression[J].Sensors and Actuators A：Physical，2007，135（2）：675-679.

[9]Dorini L B，Leite N J.Multiscale methods for image processing：the wavelet and the scale-space approaches[C]//Proceedings of the 2009 Tutorials of the XXII Brazilian Symposium on Computer Graphics and Image Processing（SIBGRAPI 2009），2009：31-44.

[10]潘泉，张磊，孟晋丽，等.小波滤波方法及应用[M].北京：清华大学出版社，2005.

[11]Cai C，Harrington P.Different discrete wavelet transforms applied to denoising analytical data[J].Journal of Chemical Information and Computer Sciences，1998，38（6）：1161-1170.

[12]王芳，鲁顺昌.小波软硬阈值去噪算法的研究及改进[J].信息技术，2008（6）：124-131.

[13]杨坦，周化雨，关履泰.抑制震荡的自适应小波阈值去噪方法[J].中山大学学报：自然科学版，2005，44（6）：15-19.

[14]Huang N E，Shen Z.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London Series A-Mathematical Physical and Engineering Sciences，1998，454（1971）：903-995.

[15]Boudraa A，Cexus J.Denoising via empirical mode decomposition[C]//Proceedings of the IEEE International Symposium on Control Communications and Signal Processing，Marrakech，Morocco，2006：4-8.

[16]吴俊，张榆锋.经验模态分解和小波分解滤波特性的比较研究[J].云南大学学报：自然科学版，2012（3）：285-290.