数控强力旋压机的直线同步进给驱动控制
2015-02-24尤娜娜辛世界
尤娜娜,辛世界
(山东理工大学机械工程学院,山东淄博 255049)
以3D65CNC三旋轮卧式强力旋压机床的同步控制技术为应用背景,对纵向进给伺服系统中双电机的同步控制进行研究,重点研究如何提高同步控制性能。通过分析旋压机传统“旋转电机+滚珠丝杠”的驱动方式,了解到传动零部件间的间隙和摩擦等因素对系统造成相应的误差,而且结构复杂,所以难以满足机床高效率、高精度的要求;而直线电机伺服系统可以取消变速箱等中间机械传动机构,减小传统传动方式中存在的摩擦力以及反向间隙,还可以弥补传动机构刚度不足的缺点。数控旋压机的双轴同步控制,受模型参数变化、摩擦力、轴间耦合性和各轴增益参数不匹配等诸多不确定性干扰因素的影响,使双电机同步运行不仅要保持各单轴的高品质控制,而且要实现双轴间的相互协调问题,于是有必要研究高精度的同步控制理论和实现方法。由于单轴具有良好的伺服系统是双轴保持同步状态的重要前提,针对直线电机非线性、参数时变、强耦合和附加扰动等因素的影响,采用无模型自适应控制和伪微分反馈 (PDF)控制方法对单轴直线电机进行控制,同时采用变论域模糊PID控制的方法对双直线电机的位置误差进行补偿,最后通过Simulink仿真软件验证该方案的可行性,其研究成果对我国旋压机床的设计制造具有一定的指导意义。
1 永磁同步直线电机数学模型
永磁同步直线电机[1](PMSLM)是一种将电能直接转化成直线运动机械能而不需要任何中间转换机构的装置。其基本结构及直线式交流伺服系统的结构和原理详见文献 [2]。电磁力控制[4]是使永磁同步直线电机进给驱动控制系统实现高动态性能的基础,其前提是建立永磁同步直线电机的数学模型,d、q轴模型电压方程式和电磁力的表达式分别为:

式中:Vd、Vq分别为初级d轴和q轴电压;Ra为电枢绕组电阻;p为微分算子;τ为永磁体极距;vr为动子速度;id、iq分别为d轴和q轴电流;ψd、ψq分别为d轴和q轴磁链;Ld、Lq分别为d轴和q轴电感;ψf为永磁体励磁基波磁链;Fe为电磁推力。
机械运动方程为:
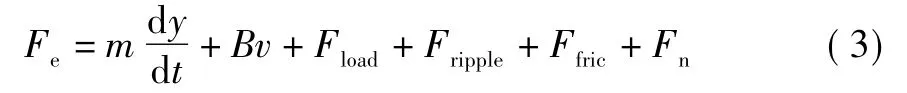
式中:m为动子质量;B为黏滞摩擦因数;v为动子线速度;Fload为负载阻力;Fripple为推力波动;Ffric为摩擦力;Fn为其他非线性扰动。
2 系统设计
旋压机主轴箱的进给运动是由两台永磁同步直线电机同步驱动实现的,存在很强的机械耦合性[5]。由于作用在两台直线电机上的负载不会严格地相同,那么当负载处于动态变化时,便引起电机速度不同步,从而引起位置不同步。采用基于补偿原理的并联同步控制方式:并联式同步控制结构与主从控制相结合的同步控制方式,通过对控制变量的调整,使其恢复到同步状态。
2.1 单轴控制器的设计
高性能的位置伺服系统要求无稳态静差、跟踪精度高、抗干扰能力强和鲁棒性好。单轴子系统的位置控制器采用无模型自适应控制,该方法属于典型的数据驱动控制。
速度控制器采用伪微分反馈 (PDF)控制器,PDF控制将所有的误差信号进行处理,响应速度较慢,但由于积分增益大,所以PDF控制相比传统的PID控制具有超调量小、抗干扰性好和鲁棒性强的优势。
无模型自适应控制本身有着严格的理论体系保证控制的稳定性,它考虑任意SISO的非线性系统,对其利用动态线性化方法,得出系统带有时变因子的线性模型族,称为泛模型[6];利用泛模型来设计控制器,控制器的运行过程[7]是:控制器输出→系统输出→时变因子辨识→调整控制器。有关的数学证明见文献 [8]。
无模型控制律设计依赖的泛模型:

考虑控制输入准则函数为:

其中:λ>0是权重因子,用来限制控制输入量的变化;y*(k+1)为期望的输出信号。
将式 (4)代入准则函数 (5)中,对u(k)求导并令其等于零,得到如下的控制算法:

其中:ρ∈(0,1]是步长因子,其目的是使控制算法更具一般性。
定义伪偏导数估计准则函数为:

其中:μ>0是权重因子。
对式 (7)关于φc(k)求极值,得到伪偏导数的估计算法:

其中:η∈(0,1]是步长因子,其目的是使该算法具有更强的灵活性和一般性,(k)为伪偏导数φc(k)的估计值。其中估计算法 (8)中的μ是对伪偏导数估计值变化量的惩罚因子。
采用Simulink模块搭建加嵌入S-function的方法。Simulink模块的搭建如图1所示。
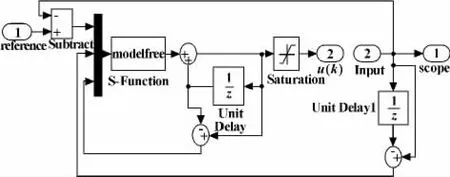
图1 MFA控制器的内部结构
2.2 同步控制器的设计
针对两台直线电机的协调控制问题,在双轴之间增加变论域模糊PID控制器。该控制器结合PID控制和模糊控制的优点,与常规的模糊PID控制器相比,增加了论域调整机制,即在模糊规则形式不变的前提下,通过伸缩因子使论域随着误差的增大而扩张,随着误差的减小而收缩,从而增加规则数,大大提高系统的控制精度。变论域模糊PID控制系统结构图如图2所示。
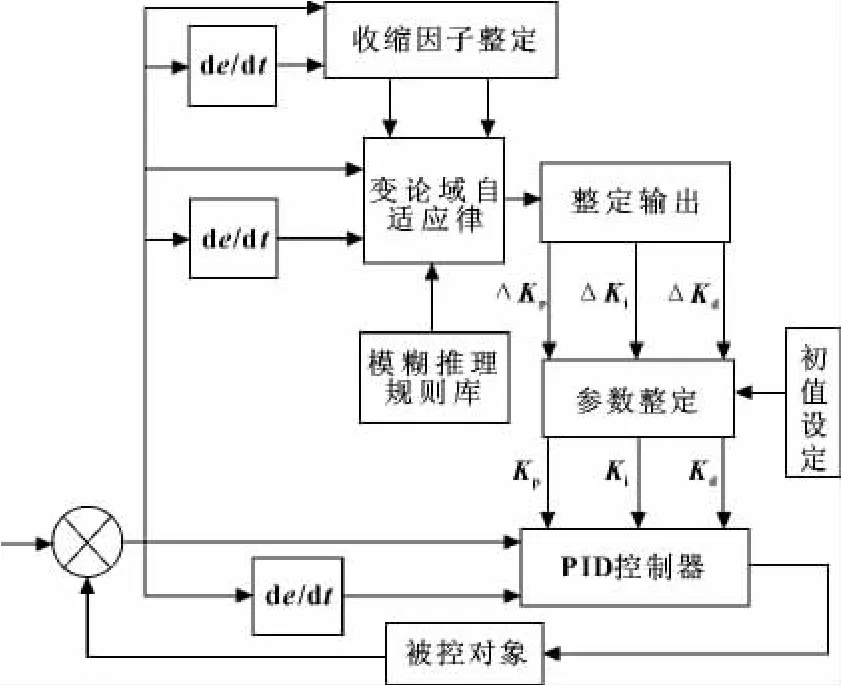
图2 变论域模糊PID控制系统结构图
变论域模糊PID控制器以位置同步误差e和位置同步误差变化率ec作为输入变量,其基本论域为Xi=[-E,E],i=1、2(i取值1、2时分别为误差e和误差变化率ec的基本论域);以PID控制器的3个参数的Kp、Ki、Kd作为输出变量,其基本论域为Yj=[-U,U],j=1、2、3(j取值1、2、3时分别为输出变量Kp、Ki和Kd的基本论域)。e、ec、Kp、Ki、Kd模糊子集均为 {NB,NM,NS,ZO,PS,PM,PB},对应的语言值分别取为 {负大,负中,负小,零,正小,正中,正大},所有变量均采用三角形隶属度函数。采用变论域控制思想,模糊论域为Xi=[-α(x)E,α(x)E],Yj=[-β(x)U,β(x)U],其中α(x)和β(x)分别为输入、输出变量论域的伸缩因子,其定义均采用如下表达式:

其中: λ∈ (0,1),k>0。
模糊控制规则是模糊控制的核心,根据3个输出参数对系统输出特性的影响情况,制定输出参数的调整原则[9]:当e较大时,为加快系统的响应速度,应适当调大Kp和调小Ki,为减小系统超调量,应适当调小Ki;当e中等大小时,为减小系统超调量和保证一定的响应速度,应适当调小Kd;当e较小时,为减小稳态误差,应适当调大Kp和Ki,为避免输出响应在设定值附近震荡和考虑系统的抗干扰性能,则调整Kd值使ec较大时,Kd取较小值,通常Kd为中等大小。根据系统的实际情况,结合旋压机纵向进给系统的操作规律及前人经验,制定参数Kp的控制规则表,如表1所示,规则略,模糊推理与解模糊的方法采用重心法。
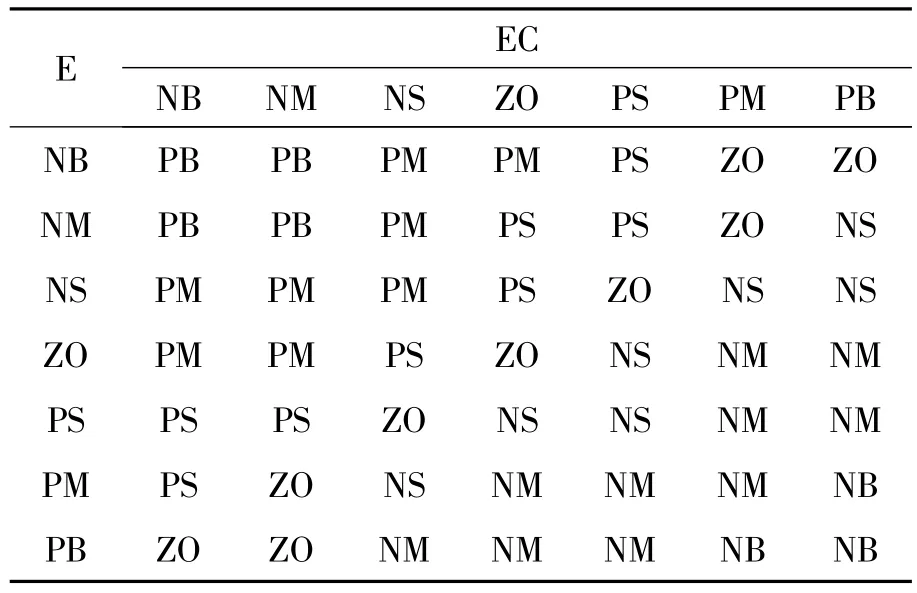
表1 Kp的控制规则表
3 系统仿真
使用Simulink对提出的方案进行验证。仿真中选用的永磁直线同步电机的参数如下:m1=400 kg,B1=1 N·s/m,Kf1=100 N/A,Kf2=100 N/A,KP1=40,KI1=115,Kp2=40,KI2=115,m2=400 kg,B2=1 N·s/m。输入变量的量化因子为:qe=3,qec=3;输出变量的比例因子为:qp=0.05,qi=0.05,qd=0.05。伸缩因子中取参数k=0.6,λ=0.5。利用Simulink模块进行仿真,位置控制器的学习因子和惩罚因子在仿真中确定,仿真框图如图3所示。两个伺服系统采用相同的阶跃输入信号,并给PMLSM施加干扰,在t=0.2 s时,给PMLSM1施加100 N的阶跃扰动;在t=1 s时,给PMLSM2施加100 N的阶跃扰动。
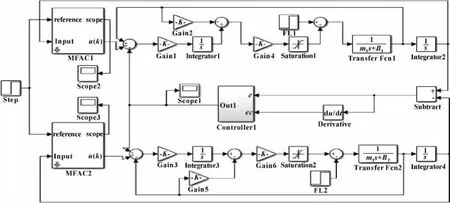
图3 双直线电机同步控制Simulink仿真框图
仿真结果如下:由图4、图5可知,当给系统施加扰动时,系统产生了同步误差,其中PID控制的位置同步误差限制在7.8 μm左右的范围内,模糊自适应PID控制的位置同步误差限制在0.8 μm左右的范围内,但误差很快趋于零,系统又重新回到稳定状态。由上述分析可知,文中采用的控制方案能达到要求的性能指标,响应速度快,同步性能好。

图4 PID控制的位置同步误差曲线
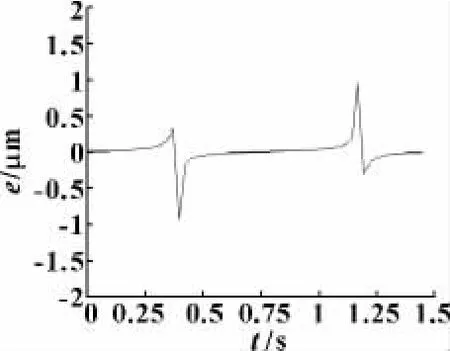
图5 模糊自适应PID控制的位置同步误差曲线
4 结束语
将无模型自适应控制、伪微分反馈控制和变论域模糊PID控制应用于双直线电机同步驱动的强力旋压机中,设计了无模型自适应控制器、PDF速度控制器和变论域模糊PID同步控制器。同步控制系统的数学模型简单,控制器运算不复杂。仿真结果验证了该方法的可行性,同步控制的精度得到了明显提高。
[1]侯忠生,金尚泰.无模型自适应控制[M].北京:科学出版社,2013.
[2]寇宝泉,程树康.交流伺服电机及其控制[M].北京:机械工业出版社,2008.
[3]马航.基于迭代学习控制的直线伺服系统扰动抑制研究[D].沈阳:沈阳工业大学,2012.
[4]王骞.圆筒型横向磁场永磁直线电机电磁场与电磁力的研究[D].哈尔滨:哈尔滨工业大学,2010.
[5]许强强.双轴进给伺服交叉耦合控制的研究[D].广州:广东工业大学,2011.
[6]李传庆,刘广生.基于Matlab-Simulink的MFA控制模块开发与仿真[J].控制工程,2008(9):61-84.
[7]侯忠生.非参数模型及其自适应控制理论[M].北京:科学出版社,1999.
[8]张国良,曾静.模糊控制及其MATLAB应用[M].西安:西安交通大学出版社,2002.
[9]郑文翰,变论域模糊PID在空压机控制中的应用研究[D].昆明:昆明理工大学,2013.
