海洋升沉模拟系统设计与控制算法研究
2015-02-24黄鲁蒙张彦廷刘振东梁会高翟佳伟
黄鲁蒙,张彦廷,刘振东,梁会高,翟佳伟
(1.中国石油大学 (华东)机电工程学院,山东青岛266555;2.山东科瑞机械制造有限公司,山东东营 257067)
0 前言
海上作业的船只、平台受到海浪、潮汐、暴风雨等多种环境因素影响,因此会产生各个方向的运动[1]。高精度的模拟浮式作业设备随海浪的升沉运动是进行海洋升沉补偿设备试验研究工作的基础,比如进行采矿船扬矿管系统、海洋浮吊、海洋起重机、钻井补偿绞车等设备的试验时,首先要求试验系统能进行“造波”,即模拟船体或者平台的运动,然后研究合理的补偿方案、测试补偿设备的性能。为了实现对升沉运动的模拟功能,开发了多种方案[2-4]。
海洋钻井升沉补偿装置只考虑平台的垂直上下运动,因此文中用标准的简谐运动来模拟海洋钻井平台的升沉规律,设计了一套基于电液比例阀控马达的液压绞车位置伺服系统,包括液压绞车及其配套的液压回路,实现了带载状况下的简谐运动;相对于电液比例阀控缸升沉模拟系统[5-6],具有带载能力强、运动行程基本不受限制的特点。
1 升沉运动模拟系统设计
1.1 系统原理
图1为海洋升沉运动模拟系统的原理图。

图1 升沉运动模拟原理图
由图可知,其核心是一套电液比例阀控马达系统,经过滑轮系统后,带动负载进行升沉运动。根据液压绞车转速、扭矩等性能参数,合理选用游动轮系个数,就可以实现不同负载、不同升沉规律的运动模拟。
除了驱动参数配备之外,还必须考虑电液比例方向阀的死区问题,考虑负载刚度变化、摩擦及阻尼等因素对液压控制系统的干扰,合理设计液压回路及控制算法,提高运动控制的精度与稳定性。
1.2 比例阀控马达回路设计
图2为电液比例阀控马达回路的原理图,包括液压绞车及其外部液压控制回路。设计参数:载荷3 t,升沉幅值0.8 m,周期15 s,游动轮系2X3,液压系统额定流量140 L/min,额定工作压力18 MPa。
液压绞车结构原理:由带单向平衡阀与控制制动器的高压梭阀组成的各种集成阀块、液压马达、卷筒、机架、减速器及离合器等部件组成,然后在外部配置液压源与Y型机能电磁阀即可工作,平衡阀与制动器使绞车制动可靠、定位精确。
液压绞车外部控制回路原理:液压泵8向系统横流量供液,通过控制电液比例方向阀6的开度与方向,从而控制液压马达3与液压绞车的转速与转向;使液压绞车进行周期性的正反转,带动负载往复运动,模拟了钻井平台运动规律。为了实现绞车位置的伺服控制,比例阀6采用中位O型机能,制动器4通过电磁阀5来实现刹车功能:即当电磁阀5接通油箱,液压马达两腔回路卸荷时,制动器工作。
升沉运动模拟系统完成一个位移闭环控制,方块图如图3所示。
2 数学建模
变量泵的流量-转速基本方程:

泵与比例阀间管路的流量连续性方程:

溢流阀的流量-压力特性简化为线性关系,设定压力0~2 MPa内实现溢流,溢流阀流量方程:
“亏咱们还是老乡,你是一点也不了解我啊?”马国平失望地坐下来,“老汪,我们是最要好的老乡、搭档,我从来没有求过你任何私事。今天来,是真的有要事相求,只是,我难于启齿啊!”

比例方向阀包括P、T、A、B 4个油口,各阀口的压力-流量方程:
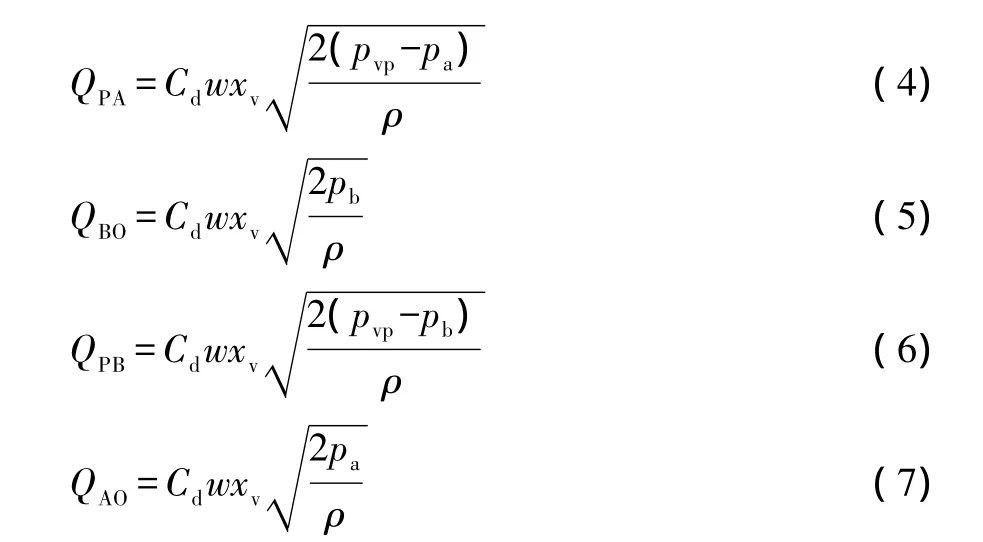
液压马达与比例阀A口之间的流量连续性方程:

液压马达与比例阀B口之间的流量连续性方程:

液压马达与比例阀B口之间的流量连续性方程:

式中:qvp为泵的实际流量;n为变量泵额定转速;D为泵排量;qp为流入管路的流量;Vg为变量泵到比例阀间管路的容积;pvp为比例阀P口压力,也即泵出口压力;QPA为比例阀从P口到A口的流量,即油源进入液压马达的流量;QPB为比例阀从P口到B口的流量;K为液压油体积弹性模量;qrv为通过溢流阀的流量;QBO为比例阀从B口到O口的流量;QAO为比例阀从A口到O口的流量;Cd为阀口的流量系数;w为阀口的面积梯度;xv为阀芯位移;pa为比例阀A口压力;pb为比例阀B口压力;pa为比例阀A口压力;Qzd为液压马达实际流量;Va为液压马达与比例阀间管路的容积;qa为比例阀A口的流量;qb为比例阀B口的流量;Vp为液压马达排量;Te为液压绞车负载扭矩;Je为液压绞车转动惯量;np为液压绞车转速。
3 控制算法对比研究
为了提高系统的控制精度、稳定性,开展控制算法的研究,分别设计了PID与模糊PID控制算法,并根据系统数学模型进行了算法的仿真对比研究。
3.1 PID控制
计算机控制系统的发展使得数字PID算法灵活性更强,实现了多种改进算法,可以满足不同系统要求。PID控制规律离散化为差分方程的形式:

式中:u为控制器输出信号;e为偏差信号;KP为比例增益;KI为积分增益;KD为积分增益;T为采样周期;k为采样序号。
PID控制器微分信号的可改善系统动态特性,加快系统的动作速度,但也易引入高频干扰,在误差扰动突变时尤其显出微分项的不足,因此采用以比例P控制为主,加入较小的微分D与积分I控制为辅。
选取微分系数D=0.1,积分系数I=0.05,分别取比例系数P=10、20、30,先忽略比例阀死区的影响,升沉运动模拟的误差曲线如图4所示。

图4 PID控制的误差曲线
由于液压系统的滞后性与液压缸换向时的压力波动现象,升沉模拟曲线局部有振动;比例系数越大、补偿效果越好,但曲线振动加剧,导致比例阀振动严重;加入比例阀死区后,曲线的震动现象更为严重。因此振动现象制约了系统的稳定性与控制精度,单一PID控制难以达到理想的效果。
3.2 模糊PID控制
PID的参数整定一直是一个难题,并且一组PID参数也难以适应系统的整个控制过程,当控制对象参数变化后,系统的调节性能也会受到影响,因此引入模糊控制理论。模糊PID控制器经过模糊推理形成查询表,在线调整PID参数,使PID控制器适应被控对象的变化,并获得良好的控制性能[7]。模糊 PID控制原理见图5。
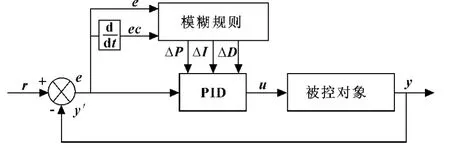
图5 模糊PID控制的原理
利用模糊理论对比例P与微分D系数进行在线整定;考虑常用的PID参数整定原则,结合该系统的仿真控制经验,制定如下模糊整定原则:
(1)当误差|e|较大时,不论误差的变化趋势如何,控制器的比例系数都取较大值,以提高响应速度,微分系数取值较小;
(2)当误差|e|在中等大小时,为保证系统相应速度并控制超调,应减小比例系数,微分系数取值较大。
(3)当误差|e|较小时,为保证系统具有良好稳态特性,应加大比例系数、微分系数,的取值与|ec|相适应;
(4)考虑比例阀死区补偿,采用PID控制和死区P控制相结合的方法。
选择PD型的模糊控制器;首先确定输入输出论域与词集,考虑系统控制的对称性,采用升沉运动模拟误差e及其微分ec作为输入量,PID控制器比例与微分增益的变化量ΔP、ΔD作为输出量;然后定义模糊子集与模糊控制规则,最后进行模糊决策,得到模糊控制输出查询表,其中比例系数增益ΔP的模糊输出查询表见表1。

表1 ΔP模糊控制输出查询表
3.3 控制效果对比
电液比例方向阀与伺服阀相比,具有抗污能力强、工作可靠的优势,但性能上有一定差距,最大问题是存在死区,因此需要对死区进行补偿[8]。
补偿方法:采用模糊PID算法,通过整定模糊控制表,使当比例阀运行在死区时,采用单一的比例控制,并且加大比例系数,提高运动跟踪速度,其它位置根据模糊控制表格采用模糊PID控制;如图6所示,取比例阀上下行程死区均为1.5 V,模糊PID控制明显比常规PID(P=10,I=0.05,D=0.1)控制的精度高、稳定性好、振动明显减小。
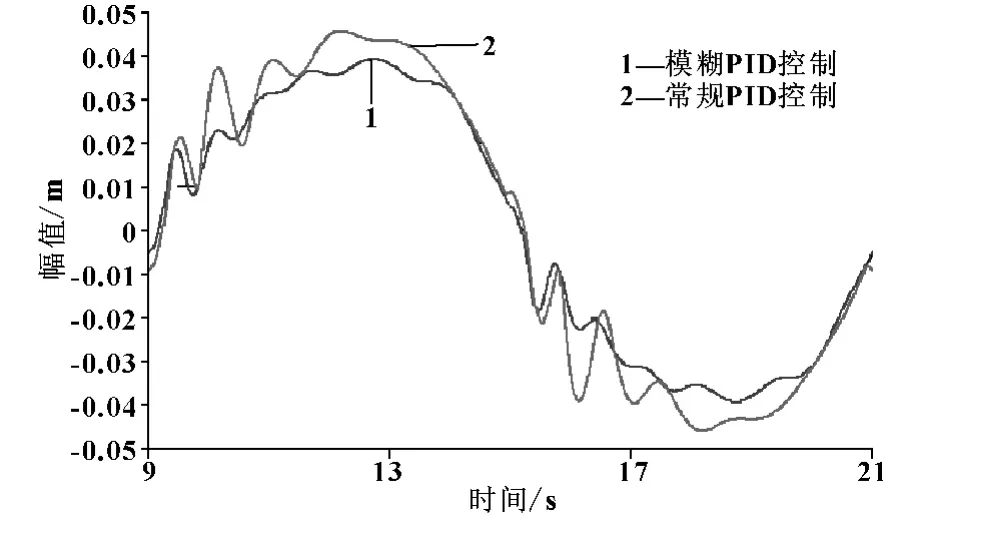
图6 控制误差曲线对比 (考虑比例阀死区)
4 实验
实际搭建了升沉模拟液压系统,采用上位机+PLC的控制模式,PLC采集液压绞车的角位移信号并传递给上位机,在上位机控制软件中编制带死区补偿的模糊PID算法,然后输出电信号来控制电液比例方向阀的开度及方向,实现闭环控制。
模糊内模PID的本质是将控制经验总结成模糊规则,从而实现分段PID控制;但是总结模糊规则要求不仅具有丰富的工程经验,还要进行大量的调整工作。为了简化算法的调试工作,试验控制参数采用的调试路线:首先建立补偿绞车样机的数学模型,并利用内模算法进行单一PID参数的初步整定;其次通过在线调试,对初始PID参数进行修正,改善控制效果;然后根据大钩位移及大钩速度对系统实行分段PID控制,先将系统分为两段,然后采用逐步细化的方式来完善控制算法。
为保证位置控制精度,是比例阀芯快速通过死区,采用了带死区补偿的分段PID控制:死区以外的位置采用PID控制;死区范围内仅采用比例控制,并提高比例系数,不同幅值时的死区控制参数经验值见表2;此外由于上下运动的受力情况不同,PID参数要按照运动方向分为两段。

表2 不同升沉幅值时的死区控制参数
升沉幅值800 mm时,带死区补偿的分段PID与单一PID实验效果对比曲线如图7所示,带死区补偿的分段PID控制明显比较稳定、误差小。
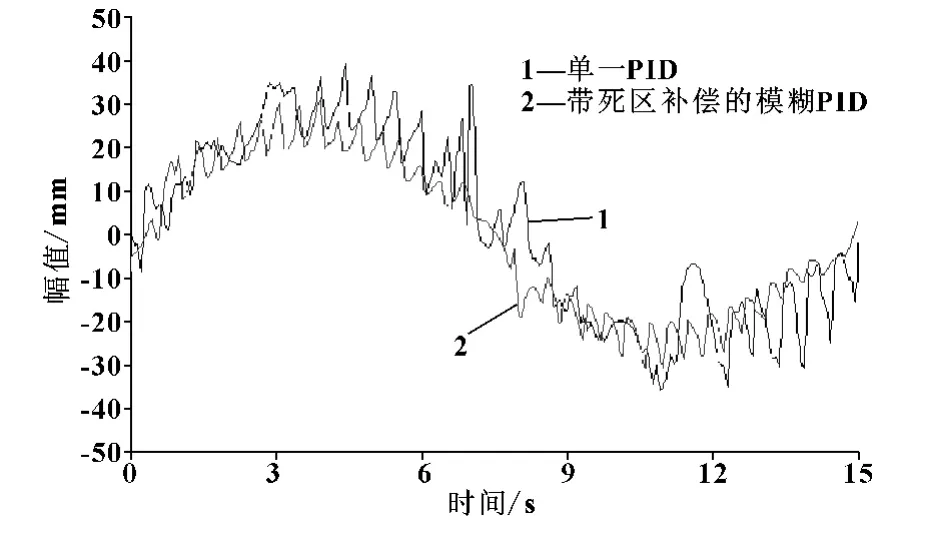
图7 升沉模拟实验误差曲线
5 结论
设计了一套基于电液比例阀控马达的液压绞车位置伺服系统,该系统可以实现不同负载、不同升沉规律的运动模拟。设计了带死区补偿的模糊PID控制算法,仿真与实验结果表明:该算法通过死区补偿、分段PID控制方式改善了系统性能,提高了系统的稳定性与控制精度。
[1]董艳秋.深海采油平台波浪载荷及响应[M].天津:天津大学出版社,2005.
[2]吴百海,肖体兵,龙建军,等.深海采矿装置的自动升沉补偿系统的模拟研究[J].机械工程学报,2003,39(7):131-132.
[3]陈建民,蔡淳鹏,刘彦武.基于虚拟仪器技术的海上实时自动调平系统设计[J].船海工程,2009,38(2):125-128.
[4]施昕昕,常思勤.一种新型6自由度运动平台的控制研究[J].机械工程学报,2014,50(3):56-61.
[5]姜浩,刘衍聪,张彦廷,等.浮式钻井平台升沉模拟系统设计[J].机床与液压,2012,40(1):85-88.
[6]李洪人,关广丰,郭洪波,等.阀控非对称缸的非线性建模及其反馈线性化[J].机械工程学报,2007,43(9):33-38.
[7]张贵,黄静华,夏永胜.基于PLC的电液比例伺服系统模糊 PID 控制研究[J].机床与液压,2014,42(1):83-85.
[8]董刚,杜京义,贾涛,等.液压比例伺服系统中死区的控制[J].机床与液压,2008,36(11):62-63.
