润滑油层流稳定性的实验研究

2015-02-24廖中文高俊文王海林

机床与液压 2015年23期

廖中文，高俊文，王海林

(1.广东农工商职业技术学院机电系，广东广州510507;2.华南农业大学工程学院，广东广州 510642)

0 前言

层流失稳是一种导致轴承的摩擦阻力矩迅速增加，功耗增大，并使轴承的工作性能大大恶化，严重时会发生轴系断裂，造成严重事故的工程现象。如何进行减阻，推迟层流失稳对应的剪切速度，具有非常重要的现实意义［1－5］。本文作者通过自制的高速可视化剪切黏度测试仪，测试两种常见油品剪切黏度及观测层流失稳对应的剪切速度，并通过改变高分子添加剂的分子量、添加量检验高分子添加剂对润滑油层流失稳产生的影响。并引入Taylor-Couette流对聚合物添加剂的减阻问题进行研究，在王海林教授的基础上优化有效黏度模型［7］，进一步分析高分子添加剂对Taylor-Couette流的稳定性的影响，探讨减阻机制。

1 剪切黏度测试仪

剪切黏度测试仪为一台外圆筒固定，内圆筒旋转的同心圆柱滑动轴承试验台，如图1所示［8］。其中，内圆筒采用白色尼龙材料，外圆筒采用有机玻璃制成。试验台架的主要结构尺寸如表1所示。

图1 高速可视化黏度测试仪的结构示意图

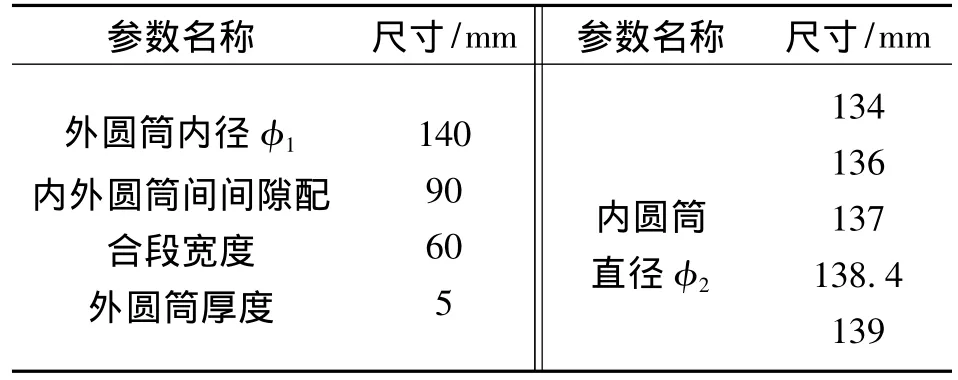
表1 高速可视化剪切黏度测试仪的主要结构尺寸

由于实验装置共配有外径分别为134、136、137、138.4、139 mm的五组内转筒，每组外径对应有中间高度分别为60 mm和90 mm的转筒。其中同一组转筒的外形除了中间高度不同，其余部分均相同。实验过程中，首先通过空转测得各个转筒的摩擦阻力矩，再将在油品中测得的剪切力矩减去空转对应的摩擦阻力矩，即可得到剪切阻力矩;接下来，通过对同一组两个转筒测得同一油品的剪切阻力矩相减，可消除上下边界处二次流的影响，从而得到不同间隙对应30 mm宽的强剪切流的纯剪切力矩。

2 高分子添加剂对层流失稳影响的实验研究

首先，通过试验讨论内圆筒中间高度、内外圆筒间间隙对润滑油层流失稳的影响，然后通过改变添加剂的浓度、分子量，检测高分子添加剂对层流失稳的影响，并通过拍照目测失稳过程。

2.1 内圆筒中间高度对润滑油层流失稳的影响

实验选用直径分别为137、138.4 mm，中间高度分别为90、60 mm的内圆筒共4个;测试温度为40℃。得到美孚速霸2000剪切力矩对应剪切速度的变化情况如图2、3所示。

图2 美孚速霸2000润滑油剪切力矩对应剪切速度曲线(内圆筒直径137 mm)

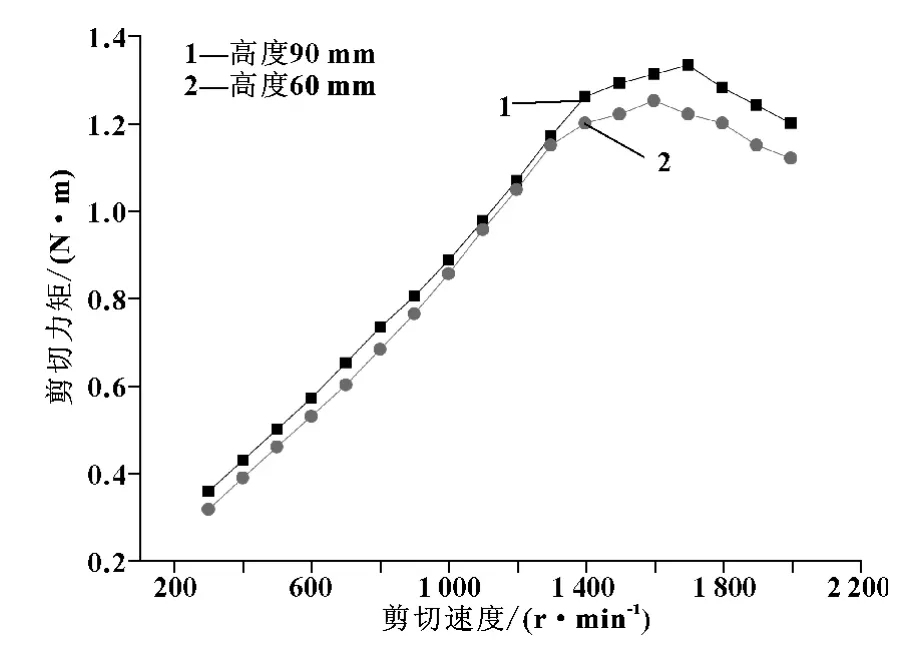
图3 美孚速霸2000润滑油剪切力矩对应剪切速度曲线(内圆筒直径138.4 mm)

通过图2、3可知，高度为90 mm的内圆筒相比高度的60 mm的内圆筒，层流失稳出现时对应的转速要高，主要原因是端部流体扰动大，层流失稳一般都是首先出现在端部，内圆筒的中间高度越高，端部效应的影响就越弱，所以实验测试过程中，90 mm内圆筒测试得到层流失稳对应的剪切速度就要高于60 mm内圆筒测试得到层流失稳对应的剪切速度。同时，比较图2和图3中的两条曲线可以发现，由于端部效应的存在，90 mm高度的内圆筒与60 mm高度的内圆筒测得的剪切力矩值并不随圆筒中间高度成正比例增长。

2.2 内外圆筒间间隙大小对润滑油层流失稳的影响

实验选用中间高度为90 mm，直径分别为136、137、138.4 mm的内圆筒;对应的间隙δ分别为2、1.5、0.8 mm;测试温度为40℃。得到润滑油美孚速霸2000剪切力矩对应剪切速度的变化情况如图4所示。

图4 不同间隙下美孚速霸2000剪切力矩对应剪切速度曲线

通过比较图4中的3条曲线，可以发现，3个不同直径的内圆筒高速旋转过程中，间隙小的内外圆筒间的润滑油相对来说进入层流失稳对应的速度要稍大一些 (间隙为2、1.5、0.8 mm对应的层流失稳点分别为780、820、900 r/min)。三者之间的主要差别体现在直径越大的内圆通进入Wavy涡及湍流区后，剪切力矩的波动不大，可以理解为间隙大的内圆筒由于剪切压力相对较小，速度达到一定的时候，对润滑油油膜的破坏性相对要小一些。

2.3 添加剂的浓度对润滑油层流失稳的影响

实验选用质量分数分别为2%、4%、5%的聚异丁烯，直径为137 mm(中间高度90 mm)的内圆筒，测试温度为50℃，得到不同浓度高分子添加剂的润滑油剪切力矩对应剪切速度的变化情况如图5所示。

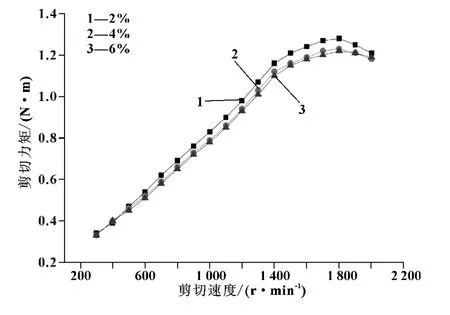
图5 不同添加剂浓度下美孚速霸2000剪切力矩对应剪切速度曲线

通过比较图5中的3条曲线，可以发现，小分子量的高分子添加剂对润滑油膜也具有一定湍流减阻性能，由图中可以发现，用量相对较大的油品进入层流失稳对应的剪切速度及进入湍流区对应的剪切速度都要大一些，抗剪切稳定要好一些。

另外，通过比较3条曲线不同剪切速度范围下对应剪切力矩的变化情况，可以发现，添加剂的减阻性能主要表现在高速区，而在层流区，它对流场的摩擦阻力矩几乎没有影响。

2.4 添加剂分子量对润滑油层流失稳的影响

实验选用直径为137 mm，中间高度分别为90 mm的内圆筒;测试温度为50℃;往润滑油美孚速霸2000中添加质量分数分别为2%，分子量分别为1 200，2 100，2 400的聚异丁烯。得到剪切力矩对应剪切速度的变化情况如图6所示。

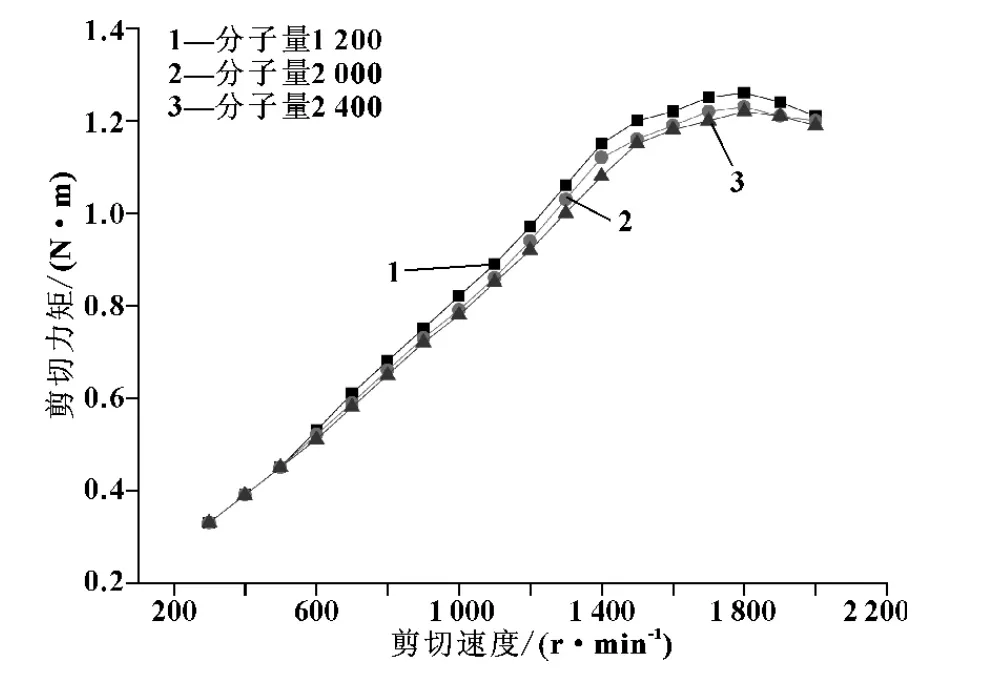
图6 不同分子量添加剂下美孚速霸2000剪切力矩对应剪切速度曲线

为了便于比对，现将未添加任何高分子添加剂的美孚速霸2000的剪切力矩对应剪切速度的曲线作为参照，如图7所示。

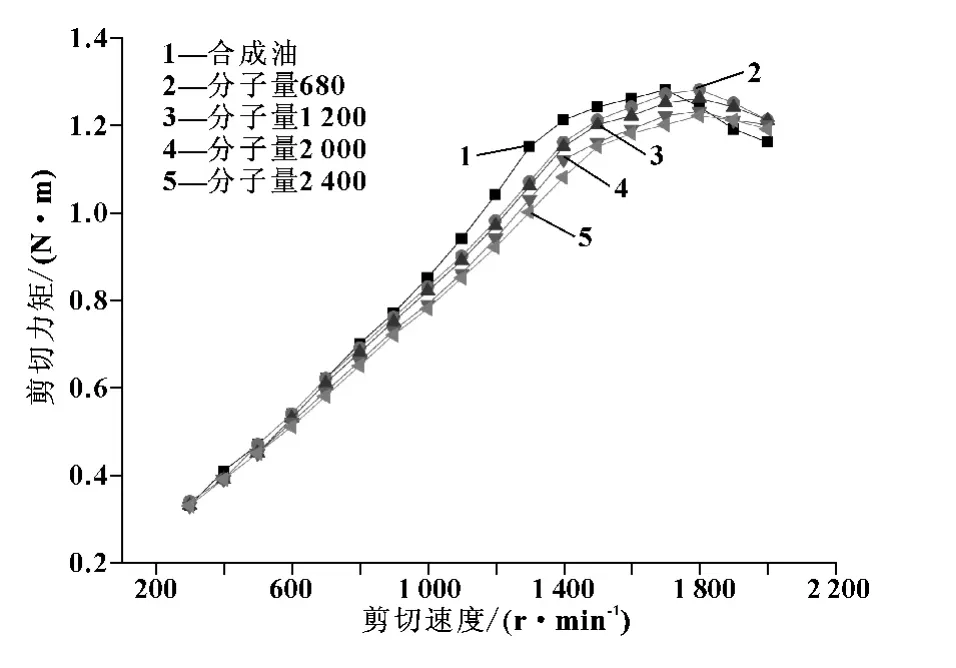
图7 不同分子量添加剂下美孚速霸2000剪切力矩对应剪切速度曲线

通过比较图7中的5条曲线，可以发现，5种不同的油品在测试过程中，剪切力矩都会发生线性增长→加速增长→增长减缓→负增长这几个阶段，可以认为，5种油品都经历了层流 (Couette流)→Taylor涡→Wavy涡→湍流的变化历程，添加剂的作用只是推迟了各个变化的转变点。

另外，通过比对几组不同的曲线，可以发现，高分子添加剂改善了润滑油的剪切稳定性，并且分子量大的高分子添加剂的湍流减阻性能要好于小分子量的高分子添加剂。

2.5 失稳过程的目测结果

实验观测了多种试样的层流失稳过程。实验发现，随着转速的提高，几种试样的流态均出现了类似的变化过程，图8、9分别为润滑油美孚速霸2000和加有质量分数为4%的聚异丁烯 (分子量680)的美孚速霸2000的流态变化过程中的典型照片。可以看到，在转速较低时流态呈稳定的层流，即Couette流。当转速达到一定值时，在轴承的轴向上出现稳定的环状涡动，即所谓的Taylor涡。Taylor涡的发生首先出现在轴承的两端，这主要是由于轴承端部流体的扰动较大的缘故。在该实验装置条件下，由于端部密封，其扰动不是很大，所以这种状态只保持了较短的时间，环状涡流便出现在整个轴向方向上。实验发现环状涡流是一种稳定的流动，它不随时间变化。如果转速进一步提高，在圆周方向上也出现了波动，这是一种随时间周期变化的涡动，即所谓的Wavy涡。这种涡动状态随转速的提高，涡动会越来越剧烈，直到出现紊乱无序的流态，即进入湍流区。高分子添加剂并没有使流态的这个变化历程发生质的变化，所不同的是，由于添加剂的作用，多种流态的转变点比基础油的要晚，也就是说，高分子添加剂推迟了流体的层流失稳。

图8 润滑油美孚速霸2000的油膜层流失稳过程

图9 质量分数4%的聚异丁烯美孚速霸2000的油膜层流失稳过程

3 有效黏度模型

将少量的高分子添加剂加入牛顿流体中，使溶液具有黏弹性的特点，并且高分子添加剂的加入会导致流体的内部剪切力发生变化。在剪切速度较低时，剪切力较小，高分子添加剂在溶液中以卷曲状存在，剪切力增大时，高分子链被拉长，溶液的拉伸黏度增加。在此，优化简单有效黏度模型。

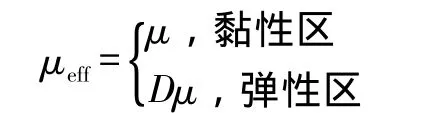
式中:μeff为有效黏度，D为与减阻效应有关的参数。

有效黏度的确定:牛顿流体中加入高分子添加剂后，会呈现黏弹性质，对于牛顿流体，其剪切应力为:

对于黏弹性流体，其剪切应力为:

令无量纲剪切力变化率的绝对值与无量纲流速梯度的绝对值的比值是α，即

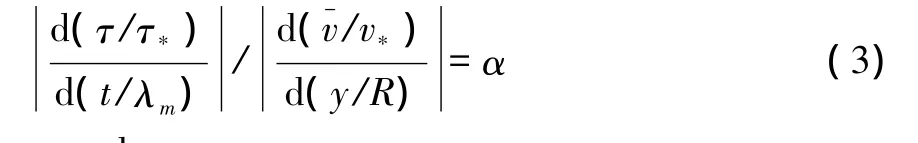
式中:τ*为壁面剪切力，τ*=ρv2*，v*为摩阻流速;λm为高分子添加剂松弛时间;R为内圆柱半径，其他同上。

令:

则有:

由公式 (5)确定减阻系数D后，便可求出有效黏度。

接下来，确定减阻系数D，D值得大小取决于比例系数α、雷诺数、溶液分子松弛时间。

α值的大小随高分子添加剂的分子量、浓度而变化，对于给定的溶液，其浓度增加，α值减小，假设，

式中:cw为重量比表示的溶液浓度;β为比例系数。

积分处理得，

其中，α0为浓度趋近于零时的α值;

雷诺数Re:

综合Rouse基于线性分子理论导出聚合物分子松弛时间及James公式，可以得到

式中:［η］为溶液本征黏度，cm3/g;c为溶液的浓度，cm3/g。

联立以上方程，可以得到:

当取直径为137 mm的内圆筒与外圆筒配合工作时，间隙比为0.021 4，添加剂为分子量680的聚异丁烯，通过计算发现，质量分数为2%时，其临界泰勒数为61.2，质量分数为4%时，其临界泰勒数为62.4，质量分数为5%时，其临界泰勒数为62.7，从中可以发现，浓度增加时，其临界泰勒数也随之增大，这与实验中得到的高分子添加剂具有推迟层流失稳的结论一致。