基于累积自学习机制的诱导信息条件下驾驶员路径选择
2015-02-24周代平
罗 佳,周代平,贺 琳
(重庆交通大学交通运输学院,重庆 400074)

基于累积自学习机制的诱导信息条件下驾驶员路径选择
罗佳,周代平,贺琳
(重庆交通大学交通运输学院,重庆400074)
摘要:将驾驶员视为有限理性,并以驾驶员的行程时间感受作为决策收益,建立基于累积自学习机制的诱导信息条件下的驾驶员路径选择模型。通过仿真验证得出不同初始状态下的模型博弈平衡结果。仿真结果表明:诱导信息的发布并不是一直有效的,它与路网的车流总量以及初始流量的分配密切相关。
关键词:诱导信息;累积自学习机制;驾驶员路径选择
博弈论中复杂的逻辑分析,使其在交通领域得到广泛的应用。文献[1]建立静态博弈模型,研究诱导信息的出行者选择路径的可能;文献[2]运用博弈论的概念与方法,剖析驾驶员对诱导信息的反应行为,最终得到建议性诱导信息能够有效地改善博弈的结果;文献[3]针对诱导系统提供无诱导信息、完全诱导信息、描述型诱导信息和建议型诱导信息4种情况的驾驶员反应行为建立博弈论模型。以上研究都将驾驶员视为完全理性,与实际情况略有差异。由于诱导信息是建议性信息,因此当发布诱导信息时,驾驶员可以选择接受和不接受诱导信息,并且驾驶员在做出路径选择策略时会受到其他驾驶员决策的影响,驾驶员之间彼此存在博弈的关系。
本文将驾驶员视为有限理性,分析讨论诱导信息条件下基于累积自学习机制的驾驶员路径选择问题。
1自学习机制
虽然驾驶员在出行前追求的是自身利益的最大化,但是在做出路径选择时驾驶员之间存在博弈关系,因此有必要将博弈思想引入驾驶员出行路径选择的问题中[4]。交通出行是一项复杂的社会活动,受驾驶员自身的局限性限制(如信息了解不全面、判断不准确等),驾驶员在作出决策时并不是完全理性的,故应将驾驶员看作是有限理性的决策者。另一方面,驾驶员每次出行对应的交通状况不是固定不变的,驾驶员要在一次次的出行中学习和调整策略,故应将出行过程看作是一个学习过程来讨论。因此,驾驶员的出行路径选择过程就是一个有限理性博弈过程。
最优反应动态模型[5]、复制者动态模型[6]和虚拟行动模型[7]是有限理性博弈中经典的三大学习模型。以上3种模型都要求局中人对其他博弈方的决策策略有一定的了解,然而在驾驶员的实际出行选择中,驾驶员很难了解到其他大部分出行者的路径选择策略,驾驶员出行路径的选择更多的决定于自身的近期经验[8]。
在出行之前驾驶员对行程时间有一个模糊预期。若驾驶员在第k次选择的路径行程时间能达到模糊预期,即驾驶员对第k次决策的收益感到满意,则第k+1次将会继续选择该路径;若驾驶员在第k次选择的路径行程时间未能达到模糊预期,则第k+1次就有可能改变决策,选择其他路径。在此机制下,博弈的演化过程中局中人是一种“自我学习”,即自学习机制。
2诱导信息条件下的累积自学习机制
2.1满意度隶属函数
出行时间的长短是影响路径选择最重要的标准[9],最常见的路段行程时间函数是美国联邦公路局函数(BPR函数)[10],其表达式为:
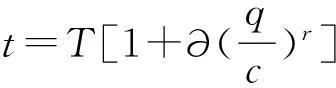
式中:t为驾驶员实际驾驶时间;T为自由行驶时(交通量为0)的路段行程时间;c为路段通行能力;q为路段实际交通量,∂、r为路段行程时间函数参数,一般取∂=0.15,r=4。
满意度是指驾驶员对从A地开往B地所花实际时间的满意程度,它是个模糊的概念。本文将驾驶员的行程时间感受作为驾驶员的路径选择收益,并将其时间感受划分成3个模糊集A1、A2、A3,运用模糊集的隶属度函数[11],其中取论域U=(0,+∞),将A1、A2、A3分别表示为“满意”、“一般”、“差”。
根据模糊集A1、A2、A3的隶属函数A1(t)、A2(t)、A3(t)[11]的计算结果,若max(A1(t),A2(t),A3(t))=A1(t),则t∈A1,驾驶员对实际驾驶时间t感觉“满意”;若max(A1(t),A2(t),A3(t))=A2(t),则t∈A2,驾驶员对t感觉“一般”;若max(A1(t),A2(t),A3(t))=A3(t),则t∈A3,驾驶员对t感觉“差”。建立路径L1和L2的时间感受收益函数E1(t1)、E2(t2),令
式中t1、t2分别为车辆在路径L1和L2上的实际行驶时间。
2.2累积自学习机制
诱导信息条件下的累积自学习机制是指在有限理性自学习机制下,第p位驾驶员第k+1次的车辆路径选择策略(是否接受诱导)取决其前k次接受诱导的累积时间感受收益和不接受诱导的累积时间感受收益,数学表达式为:
式中:Yp为第p位驾驶员前i次路径选择中,选择接受诱导的累积时间感受收益;Np为第p位驾驶员前i次路径选择中,选择不接受诱导的累积时间感受收益;Ypi为第p位驾驶员第i次路径接受诱导的驾驶员时间感受收益;Npi为第p位驾驶员第i次路径不接受诱导的驾驶员时间感受收益;Q为参与博弈的车辆总数(设每次参与博弈车辆总数不变,且每位驾驶员只能驾驶1辆车)。
若第p位驾驶员第i次接受诱导,则:Ypi=E1(t1),Npi=0。若第p位驾驶员第i次不接受诱导,则:Npi=E2(t2),Ypi=0。以choice(p,i)表示第p位驾驶员第i次的选择,choice(p,i)=1表示第p位驾驶员第i次博弈接受诱导;choice(p,i)=0表示第p位驾驶员第i次博弈不接受诱导。
若发布信息建议路径L1,有

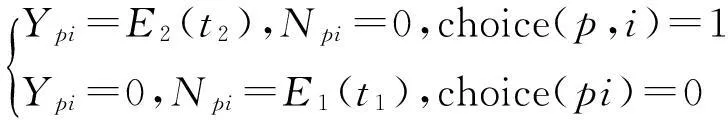

图1 路网示意图
2.3模型基本假设
以驾驶员的实际行驶时间作为驾驶员选择某条路径所获得的收益。考虑如图1所示的路网,建立虚拟路径:接受诱导路径Ly和不接受诱导路径Ln。将路径Ly、Ln、L1和L2座位化处理,即:分别将各路径划分为具有Q个座位的方格化路径。
设每次参与博弈的驾驶员总数等于Q,初始接受诱导的驾驶员比例为m,则初始接受诱导的车辆总数qy(i)=mQ,不接受诱导的车辆总数qn(i)=Q-qy(i)。将qy(i)位驾驶员随机坐在路径Ly上,将qn(i)位驾驶员坐在Ly空的位置所对应的Ln的座位上,并给每位驾驶员按照座位号标上从1~Q的号码,且保持该号码不变。若第p位驾驶员第i次选择接受诱导,即choice(p,i)=1,则在路径Ly上第p个座位为“有”,在路径Ln上第p个座位为“空”,即:Ly(p)=1,Ln(p)=0;若第p位驾驶员第i次选择不接受诱导,即choice(p,i)=0,则在路径Ly上第p个座位为“空”,在路径Ln上第p个座位为“有”,即:Ly(p)=0,Ln(p)=1;所以,若第i次发布信息建议驾驶员走路径L1,则L1(p)=Ly(p),L2(p)=Ln(p);若第i次发布信息建议驾驶员走路径L2,则L1(p)=Ln(p),L2(p)=Ly(p)。因此第i次路径L1、L2上的交通量q1(i)、q2(i)的求解公式为:
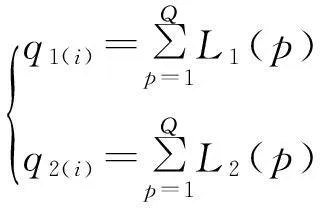
2.4收益函数模型建立
在诱导信息累积自学习机制中,第p位驾驶员的第i+1次路径选择策略取决于其自身的累积时间感受收益Yp和Np。驾驶员通过对自身前i次接受与不接受诱导的经验的累积与学习,判断选择出“有限理性的最优方案”,借以得出第i+1次是否接受诱导,即:若Yp>Np,则第i+1次驾驶员p选择接受诱导(choice(p,i+1)=1);若Yp 式中:Gi为局中人;Sp为局中人所做的决定(即策略);Up为局中人收益函数。 3模型求解算法 1)初始化模型。给C1、C2(C1>C2)、T、ζ赋值(定值),其中C1、C2分别为路径L1、L2的通行能力,T为自由流时从A到B地的行驶时间,ζ为当第p位驾驶员前k次路径选择中接受诱导的累积收益等于不接受诱导的累积收益时,驾驶员p第k+1次改变路径选择策略的概率。给m、Q赋初始值m=0.1,Q=1 000(m为路径L1的初始分配比例,初始诱导信息的建议路径为L1)。fabu(1)=1,座位化路径Ln、Ly、L1、L2,确定初始接受诱导的驾驶员qy(1)=round(mQ),不接受诱导的驾驶员qn(1)=Q-qy(1),将qy(1)名驾驶员随机坐到路径Ly的座位上,将qn(1)名驾驶员坐到对应Ly上空位置的Ln的座位上。 Ln=zeros(1,q); Ly=zeros(1,q); %座位化虚拟路径Ln、Ly L1=zeros(1,q);L2=zeros(1,q);%座位化路径L1、L2 e=ones(1,q); qy(1)=round(mq);%确定初始接受诱导的驾驶员总数 qn(1)=q-qy(1); kk=randperm(q,qy(1)); forg=1:qy(1);%将接受诱导的车辆随机坐到路径Ly上 Ly(kk(g))=1; end Ly=e-Ly;%将不接受诱导的驾驶员坐在Ln上 forg=1:q ifLy(g)==1 choice(g,1)=1; else choice(g,1)=0; end end。 2)判断第p位驾驶员第i次的路径选择策略choice(p,i)。若choice(p,i)=1,即:接受诱导,则Ly(p)=1,Ln(p)=0;若choice(p,i)=0,即第p位驾驶员不接受诱导,则Ln(p)=1,Ly(p)=0。 forp=1:q if choice(p,i)=1 Ly(p)=1; Ln(p)=0; else Ly(p)=0; Ln(p)=1; end end。 3)判断第i次诱导信息发布的建议路径。若fabu(i)=1,则L1=Ly,L2=Ln;若fabu(i)=2,则L2=Ly,L1=Ln;分别统计路径L1,L2上的驾驶员数q1(i)和q2(i)。 if fabu(i)==1 L1=Ly; L2=Ln; else L1=Ln; L2=Ly; end q1(i)=sum(L1); q2(i)=sum(L2); %统计路径L1、L2第i次博弈的流量(车辆数)。 4)计算路径L1、L2上的驾驶员时间感受,并根据第i次的发布信息得出第p位驾驶员第i次的接受诱导信息的时间感受Ypi和不接受诱导信息的时间感受Npi。 5)累积驾驶员接受诱导信息的时间感受Ypi和不接受诱导信息的时间感受Npi。 Yp=Yp+Ypi;%累积驾驶员接受诱导的时间感受收益; Np=Np+Npi,%累积驾驶员不接受诱导的时间感受收益。 6)判断Yp和Np大小,确定第p位驾驶员第i+1次的路径选择方案choie(p,i)。 7)根据choice(p,i+1)计算第i+1次接受诱导的驾驶员总数和不接受诱导的驾驶员总数,确定第i+1次发布的诱导信息fabu(i+1)。 8)判断博弈次数是否>100。若i>100,则转9),否则i=i+1,转2)。 9)判断初始接受诱导信息的驾驶员比例是否大于1。若m>1,则转10),否则m=m+0.1,转1)。 10)终止条件。若Q>3(C1+C2)则终止循环,否则Q=Q+Δq,转1)。 4模型仿真 本算例中,C1=1 500,C2=1 000,T=30,ζ=0.333[12],Q=1 000,Δq=500。仿真结果如下:(本算例中,fabu(1)=1,即第1次诱导信息的建议路径为L1)。第99次和第100次的博弈结果如图2所示。 a)第99次博弈 b)第100次博弈图2 诱导信息下累积自学习机制博弈结果 仿真结果表明:在累积自学习机制下,当参与博弈的车辆总数远大于路网总通行能力时,初始接受诱导的驾驶员比例m对博弈平衡状态无影响,其博弈结果均为峰谷平衡;当路网车辆总量接近路网总通行能力时,路网博弈平衡结果与初始接受诱导的驾驶员比例相关,其博弈结果会呈现稳定平衡或交替平衡;当路网车辆总量远小于路网总通行能力时,初始接受诱导的驾驶员比例对路网博弈平衡结果无显著影响,其博弈结果为稳定平衡。 因此,当路网车流总量小于或接近路网总通行能力时,若发布诱导信息,路径L1、L2的拥挤度接近,对路网通行能力具有较高的利用率;当路网车流总量远大于路网总通行能力时,若发布诱导信息,路网系统会形成峰谷平衡,路径L1、L2的拥挤度出现“两极化”现象,可发布诱导信息对路网总通行能力的利用率较低,可采取相应的交通管理措施,提高路网通行能力的利用率。 5结语 1)讨论了基于累积自学习机制的有诱导信息车辆路径选择问题,建立以驾驶员累积时间感受为收益函数的博弈模型,并通过仿真得出模型的博弈平衡结果。 2)当路网车辆总量接近路网总通行能力时,发布诱导信息,路网的交通流分布也能达到稳定平衡,并且对路网通行能力具有较高的利用率;在路网总流量远大于路网总通行能力或发生紧急交通事故及节假日时,发布诱导信息,路网交通流分布呈现峰谷平衡,不能有效利用整个路网系统,此时应采取相应的交通管理措施。 参考文献: [1]董斌杰,李克平,廖明军,等,诱导信息下基于博弈论的路径选择模型[J].北华大学学报(自然科学版),2007, 8(1):88-91. [2]李静,范炳全.基于驾驶员反应行为的诱导博弈分析[J].上海理工大学学报,2003, 25(4): 398-400. [3]鲁丛林.诱导条件下的驾驶员反应行为的博弈模型[J].交通运输系统工程与信息,2005,5(1): 58-61. [4]刘建美.诱导条件下的路径选择行为及协调方法研究[D].天津:天津大学,2010. [5]谢识予.经济博弈论[M]. 2版.上海:复旦大学出版社,2002. [6]王济川,郭丽芳.抑制效益型团队合作中“搭便车“现象研究——基于演化博弈的复制者动态模型[J].科技管理研究,2013,12(21):191-195. [7]刘建美,马寿峰.交通诱导-出行信号博弈分析及其虚拟行动学习模型[J].武汉大学学报(工学版),2010,40(1):102-107. [8]EREV I,BEREBY-MEYER Y,ROTH A.The effect of adding a constant to all payoffs:experimental investigation and implications for reinforcement learning models[J].Journal of Economic Behavior and Organization,1999(39):111-128. [9]OUTRAM V E, THOMPSON E.Driver route choice Proceeding[C].London:PTRC Annual Meeting ,1977. [10]杨佩坤,钱林波.交通分配中路段行程时间函数研究[J].同济大学学报(自然科学版),1994,22(1):41-44. [11]杨纶标,高英仪,凌卫新.模糊数学原理及应用[M].广州:华南理工大学出版社,2011:1-67. [12]周元峰.基于信息的驾驶员路径选择行为及动态诱导模型研究[D].北京:北京交通大学,2007. (责任编辑:杨秀红) Driver′s Route Choice with Help of Induced Information Based on Cumulative Self-Learning Mechanism LUOJia,ZHOUDaiping,HELin (SchoolofTraffic&Transportation,ChongqingJiaotongUniversity,Chongqing400074,China) Abstract:Regarding the driver as the bounded rationality and driver′s feelings of travel time as a decision benefits, a driver′s route choice model of the induced information based on the cumulative self-learning mechanism is established. The game balance results are verified by the simulation in the different initial states. The simulation results show that the induction information release is not always effective and it is closely related to the total network traffic flow and initial flow. Key words:induced information; cumulative self-learning mechanism; driver′s route choice 文章编号:1672-0032(2015)04-0034-06 中图分类号:U471.3 文献标志码:A DOI:10.3969/j.issn.1672-0032.2015.04.008 作者简介:罗佳(1993—),女,四川宜宾人,硕士研究生,主要研究方向为交通规划. 收稿日期:2015-05-22